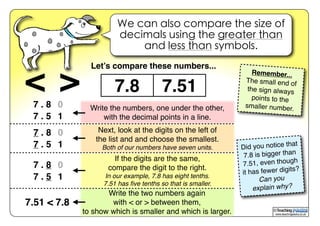
The document is about decimals and how they represent parts of whole numbers. It explains that decimals have a decimal point separating the whole numbers on the left from the part numbers on the right. It provides examples of what different decimals look like in diagrams and on a number line. It discusses rounding, adding, subtracting, multiplying and dividing decimals.

1. Hi... I am Dec.
I am a Dalmation with ten spots!
I would love to learn more about
decimals. Will you help me?
www.teachingpacks.co.uk
©

2. What are decimals?
Decimals are parts of whole things.
They are a little like fractions,
but we write them in a different way.
Decimal numbers have a decimal point.
This separates the whole numbers (on the left)
from the part numbers (on the right).
4
12
19
6
87
409
Decimal Points
Whole Numbers Part Numbers
.
.
.
www.teachingpacks.co.uk
©

3. www.teachingpacks.co.uk
©
It is important to
remember what each digit
stands for in a number.
This is called place value.
Whole NumbersWhole NumbersWhole NumbersWhole Numbers Part NumbersPart NumbersPart Numbers
Th H T U . t h th
Thousands Hundreds Tens Units
Decimal
Point
tenths hundredths thousandths
8 5 6 1 . 9 3 2
1 Thousand =
1 Hundred =
1 Ten =
1 Unit =
1 Tenth =
1 Hundredth =
10 Hundreds
10 Tens
10 Units
10 Tenths
10 Hundredths
10 Thousandths
Each place is 10 times bigger
than the place on its right.

4. www.teachingpacks.co.uk
©
What do
decimals
look like?
If a large
square shows
one whole,
this is what
some
decimals
might look
like...
One tenth
One out of ten
0.1
One hundredth
One out of a hundred
0.01
Two tenths and
seven hundredths
Twenty-seven hundredths
0.27
What decimal does
this picture show?

5. www.teachingpacks.co.uk
©
Number lines can help us
to compare decimals.
0 1 2 3 4 5
0.3 0.8 ? 2.4 3.2 ? ?
What decimal numbers are the red arrows pointing to?
1.3 1.4 1.5 1.6 1.7 1.8
1.32 ? 1.47 1.55 ? 1.73 ?
This number line shows units, tenths and hundredths.
The number line below shows units and tenths.

6. If the numbers don’t all have the same number of
digits, it might help to put a zero on the end.
Never put a zero before the decimal point though!
www.teachingpacks.co.uk
©
Putting decimals
in order is like
putting whole
numbers in order.
Remember to
line up the
decimal points
though!
3.87 2.41 1.07 2.9 3.3
3.5 3.50 5.71 5.710
Let’s put these numbers in order of size,
from smallest to largest.
Write them out, one under the other,
with the decimal points in a line.
Next, look at the digits on the left of
the list and and choose the smallest.
1.07 2.41 2.9 3.3 3.87
3 . 8 7
2 . 4 1
1 . 0 7
2 . 9 0
3 . 3 0
1.07
Then, choose the next largest.
If the digits are the same,
compare the digit to the right.
2.41 2.9
Keep going until you have put all
of the numbers in order.

7. www.teachingpacks.co.uk
©
We can also compare the size of
decimals using the greater than
and less than symbols.
7.8 7.51
7 . 8 0
7 . 5 1
Let’s compare these numbers...
< >
Write the numbers, one under the other,
with the decimal points in a line.
Write the two numbers again
with < or > between them,
to show which is smaller and which is larger.
If the digits are the same,
compare the digit to the right.
In our example, 7.8 has eight tenths.
7.51 has five tenths so that is smaller.
Next, look at the digits on the left of
the list and and choose the smallest.
Both of our numbers have seven units.
7 . 8 0
7 . 5 1
7.51 < 7.8
7 . 8 0
7 . 5 1
Remember...
The small end of
the sign always
points to the
smaller number.
Did you notice that
7.8 is bigger than
7.51, even though
it has fewer digits?
Can you
explain why?

8. Rounding a decimal means
changing it to one with
a similar (but simpler) value.
This makes it easier to work with.
3.5 3.6 3.7 3.8 3.9 4.03.0 3.1 3.2 3.3 3.4
3.4 rounded to the nearest whole number is 3.0
If you have a number that is half-way between
two whole numbers (like 3.5), we round it UP.
3.8 rounded to the nearest whole number is 4.0
Let’s round these decimals to the nearest whole number...
www.teachingpacks.co.uk
©

9. 7.615 8
7.615 7.6
7.615 7.62
www.teachingpacks.co.uk
©
To round to the nearest whole number...
7.615
Let’s try rounding...
To round to the nearest tenth...
To round to the nearest hundredth...
Look at the digit to the right of the units.
We have six tenths,
so we round the units up to eight.
Look at the digit to the right of the tenths.
We only have one hundredth,
so the tenths stays the same.
We don t always need to
draw a number line when
we are rounding decimals.
’
Look at the digit to the
right of the hundredths.
Here, we have five thousandths,
so we round the hundredths up to two.
If the next digit is
0, 1, 2, 3 or 4,
round down.
If the next digit is
5, 6, 7, 8 or 9,
round up.

10. www.teachingpacks.co.uk
©
Some decimals have digits
that repeat. These are called
recurring decimals
(or repeating decimals).
3.333333...
8.010101...
5.182182...
3.3
8.01
5.182
3.3
8.01
5.182
Here are some examples...
To save time, we use a dot
over the first and last digits
of the repeating pattern.
Sometimes we use
a line to show the
repeating pattern.
The repeating patterns
could go on forever!

11. www.teachingpacks.co.uk
©
Adding and subtracting
decimals is just like
adding and subtracting
whole numbers.
Just remember to line up the decimal points...
... and don’t forget to write the decimal point in your answer!
5 . 6
3 . 72+
1
5 . 6
3 . 72+
8 . 73
2 . 52-
9 . 32 6 . 21?

12. www.teachingpacks.co.uk
©
How do we
multiply or
divide decimals
by 10 or 100?
Multiplying by 10
T U . t h
3 . 5
0 . 3 5
Dividing by 10
T U . t h
0 . 3 5
3 5 . 0 0
Multiplying by 100
U . t h th
3 . 5
0 . 0 3 5
Dividing by 100
T U . t h
0 . 3 5
3 . 5 0
To multiply by 10, move the digits one space to the left.
To multiply by 100, move the digits two spaces to the left.
To divide by 10, move the digits one space to the right.
To divide by 100, move the digits two spaces to the right.
0.35 x 10 = 3.5
3.5 ÷ 10 = 0.35
0.35 x 100 = 35
3.5 ÷ 100 = 0.035 Remember...
1) The decimal point
doesn’t move.
2) You might need to
fill in any blank
places with a zero.

13. www.teachingpacks.co.uk
©
We multiply and divide decimals in the
same way as we do for whole numbers.
But it is easier to change the decimals
into whole numbers first...
2.3 x 7
We can change the decimal (2.3) into a whole
number by multiplying it by 10...
Now, let’s multiply 23 by 7...
2. 3x 10= 23
23 x 7= 161
2. 3x 7= 16. 1
You might use different methods to multiply and divide whole numbers. Just remember to change decimals to whole
numbers when you are multiplying and dividing them... and change the final answer back into a decimal!
Finally, we need to change the answer back
into a decimal by dividing it by 10 (because
we multiplied by 10 earlier). So...
16.5 ÷ 3
Let’s change the decimal (16.5) into a whole
number by multiplying it by 10...
Now, let’s divide 165 by 3...
16. 5x 10= 165
1665 ÷ 3= 55
16. 5÷ 3= 5. 5
We need to change the answer back into a
decimal by dividing it by 10 (because we
multiplied by 10 earlier). So...

14. www.teachingpacks.co.uk
Texture: © ThinkStock
©
17
100
0.17 17%
To convert a decimal to a percentage,
multiply the decimal by 100.
Don’t forget to write the % sign!
To convert a percentage
to a fraction,
write the number
as the numerator and
100 as the denominator.
How do we convert
fractions, decimals
and percentages?
To convert a fraction
to a decimal,
divide the numerator
by the denominator
(divide the top number
by the bottom number).

15. Fractions, decimals and percentages are
different ways of describing the same amounts.
Can you remember these?
www.teachingpacks.co.uk
©
Fraction Decimal Percentage
1 1 100%
3/4 0.75 75%
2/3 0.6 66.6%
1/2 0.5 50%
1/3 0.3 33.3%
1/4 0.25 25%
1/5 0.2 20%
1/8 0.125 12.5%
1/10 0.1 10%
1/100 0.01 1%

16. Answering money problems will
usually involve working with decimals.
Here are some things to remember...
www.teachingpacks.co.uk
Images: © ThinkStock
©
Remember...
Calculators might give an answerwith only one decimal place.
However, answers to money
questions will usually need to bewritten with two decimal places.
So... 3.9 = $3.90
3.9
Tens
(of dollars)
Dollars
Decimal
Point
Tens
(of cents)
Cents
$ 1 5 . 9 3
$1.00 = 100¢
$0.10 = 10¢
$0.01 = 1¢