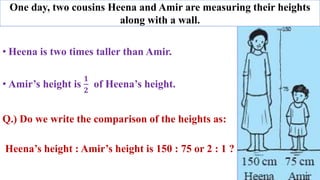
Two cousins, Heena and Amir, are measuring their heights against a wall. Heena is two times taller than Amir, and Amir's height is half of Heena's height. This information can be expressed as a ratio comparing their heights, such as Heena's height to Amir's height being 2:1 or 150:75. The document then discusses what a ratio is and provides examples of how to write and calculate ratios in different contexts.

1. Integrated B.Sc. - B.Ed.
Name : SANDHYA
School Of Education
Part 1

2. Identify the Image

3. Identify the Image
Height Chart on Wall

4. One day, two cousins Heena and Amir are measuring their heights
along with a wall.

5. •Heena is two times taller than Amir.
•Amir’s height is
𝟏
𝟐
of Heena’s height.
One day, two cousins Heena and Amir are measuring their heights
along with a wall.

6. • Heena is two times taller than Amir.
• Amir’s height is
𝟏
𝟐
of Heena’s height.
Q.) Do we write the comparison of the heights as:
Heena’s height : Amir’s height is 150 : 75 or 2 : 1 ?
One day, two cousins Heena and Amir are measuring their heights
along with a wall.

7. Ratio
The ratio is used to compare two quantities. These quantities must have the same units.
The ratio is represented by “:”, which is read as “to”.
• We can write it in the form of “fraction”.

8. Ratio

9. Ratio
In the given cases, we write the ratio of the heights as :
• Heena’s height : Amir’s height is
150 : 75 or 2 : 1
Remember that to compare two quantities, the units must be
the same. A ratio has no units.

10. List some examples from their day to-day life where they
observe ratios.
There are 6 pink chocolates to 3 blue chocolates.

11. List some examples from their day to-day life where they
observe ratios.
There are 3 cups of flour to 2 cups of milk.

12. Length and breadth of a rectangular field are 50 m and 15 m
respectively. Find the ratio of the length to the breadth of the field.

13. Length and breadth of a rectangular field are 50 m and 15 m
respectively. Find the ratio of the length to the breadth of the field.
• Length of the rectangular field = 50 m
• Breadth of the rectangular field = 15 m
• The ratio of the length to the breadth is 50
: 15
• The ratio can be written as = 10 : 3

14. Find the ratio of 3 km to 300 m.
First, convert both the distances to the same
unit.
So, 3 km = 3 × 1000 m = 3000 m
Thus, the required ratio,
3 km : 300 m is 3000 : 300 = 10 : 1

15. There are 45 persons working in a school. If the number of females is 25
and the remaining are males, find the ratio of:
(b) The number of males to number of females.

16. There are 45 persons working in a school. If the number of females is 25
and the remaining are males, find the ratio of:
(a) The number of females to number of males.
• Number of females = 25
• Total number of workers = 45
• Number of males = 45 – 25 = 20
• Therefore, the ratio of number of females
to the number of males = 25 : 20 = 5 : 4
• And the ratio of number of males to the
number of females = 20 : 25 = 4 : 5

17. There are 8 stationary items including are pens ,
are pencils and are erasers.
Find the ratio
I.) pencils to pens = 2 : 4
= 1: 2
2 2
4

18. There are 8 stationary items including 4 are pens ,2 are pencils and
2 are erasers.
Find the ratio
II.) erases to all stationary items = 2: 8
= 1: 4

19. A) 2:3
B) 3:2
C) 3:5
D) 5:3
• There are 5 pups, 2 are boys, and 3 are girls.The ratio
of girls to all pups is

20. RECAPITULATION:
• The ratio is used to compare two quantities. These quantities must have the same units.
• In the following figure, find ratios into the simplest form.
28 : 24
7: 6
35: 30
7: 6

21. RECAPITULATION:
• The ratio of 1.5 m to 10 cm is:
First, covert 1.5 cm = 1.5 × 100cm = 150 cm
Thus, the required ratio,
1.5 m : 10cm is 150 : 10 = 15 : 1
• Real life examples of Ratios :

22. HOMEWORK:
Q.1) Find the ratio of:
(a)5 to 50 paisa (b) 15 kg to 210 g
(b)9 m to 27 cm (d) 30 days to 36 hours
Q.2) Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis.
Find the ratio of (a) Number of students liking football to number of students liking tennis.
(b) Number of students liking cricket to total number of students.
Q.3) In a year, Seema earns 1,50,000 and saves 50,000. Find the ratio of
(a)Money that Seema earns to the money she saves.
(b) Money that she saves to the money she spends