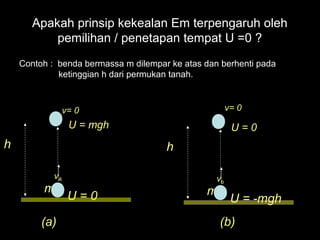
Dokumen tersebut membahas tentang usaha, tenaga, dan daya. Usaha adalah hasil kali vektor gaya dan perpindahan, sedangkan tenaga adalah kemampuan untuk melakukan usaha. Ada dua jenis tenaga yaitu tenaga potensial dan kinetik. Daya adalah laju perubahan tenaga dalam satuan waktu."

1. USAHA, TENAGA/Energi & DAYA
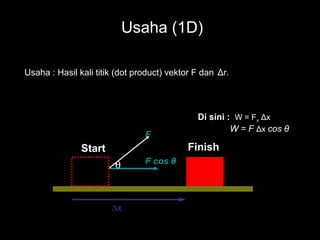
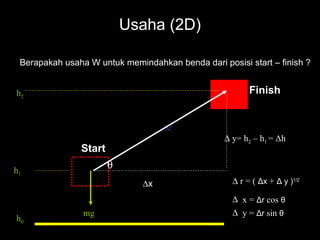
Usaha : Hasil kali titik (dot product) vektor F dan Δr.
Usaha merupakan besaran skalar.
Jika dilihat dari dimensinya, dimensi usaha = dimensi torka.
Dimensi usaha : [panjang][gaya] = [torka]
Usaha :
    torka:   
W = F • ∆r = ∆r • F τ = r ×F
Tetapi torka adalah besaran vektor, usaha
besaran skalar, jadi mereka tidak sama.

2. USAHA
Jika benda bergeser dari x1 menuju x2 dengan gaya yang bekerja pada
benda tersebut merupakan fungsi jarak F(x) maka usaha total yang
dilakukan oleh gaya F adalah :
N
Wtotal ≈ 1∆ + 2 ∆ + + N ∆N ≈
F x1 F x2 ... F x ∑∆i
Fi x
i=
1
untuk 1-D: Wtotal ≈ ∫ Fdx untuk 2D&3D: W ≈ Fdr
total ∫
F(x) Kurva fungsi F(x)
N
Wtotal ≈ ∑ Fi ∆xi
i =1
x1 x2 x

3. Usaha (1D)
• Gaya fungsi jarak F(x) Area = Fx ∆x
atau dW = F dx
Fx N
Wtotal ≈ F1∆x1 + F2 ∆x2 + ... + FN ∆xN ≈ ∑ Fi ∆xi
i =1
xf
W = ∫ F ( x) dx
∆x x xi
Start Finish
F F
θ = 0°
∆x

4. Usaha (1D)
Usaha : Hasil kali titik (dot product) vektor F dan Δr.
Di sini : W = Fx Δx
W = F Δx cos θ
F
Start Finish
θ F cos θ
∆x

5. contoh
Di sini, usaha W = F. r = Fx . r
Dimana : s2 = h2 + r2
Di sini, usaha W = F. h = Fy . h
Finish
F
s
h
r θ Start
mg

6. Usaha (2D)
Berapakah usaha W untuk memindahkan benda dari posisi start – finish ?
h2 Finish
∆r
∆ y= h2 – h1 = Δh
Start
h1
θ
∆x ∆ r = ( Δx + Δ y )1/2
∆ x = Δr cos θ
mg ∆ y = Δr sin θ
h0

7. Usaha 2D lanjutan
Ada 2 kemungkinan lintasan :
• Lintasan Δr .
• Lintasan Δx & Δy
Lintasan Δr : Wtotal = mg Δr cos (900 + θ)
= mg Δr (-sin θ) = - mg Δy = - mg Δh
Lintasan Δx & Δy : Wtotal = WΔx + Wδy
= mg Δx cos (900 ) + mg Δy cos (1800 )
= 0 + mg Δy (-1)
= - mg Δy = - mg Δh.
Kesimpulan : besarnya usaha yang dilakukan oleh gaya berat (gaya
gravitasi) tidak bergantung pada lintasan yang
ditempuh, hanya bergantung pada perbedaan tinggi

8. Gaya konservatif : gaya yang usahanya tidak bergantung
pada lintasan tetapi hanya bergantung pada letak awal &
akhir
F F
Δh
Δh
θ
(a) (b)
W(a) = W(b) = mg Δh

9. Satuan Usaha
• SI : meter newton = Nm = joule = J
• Cgs : cm dyne : erg
1 J = 1mN = (102 cm)(105 dyne)
= 107 cm dyne
Atau 1 J = 107 erg

10. Tenaga (Energi)
Tenaga = kapasitas/kemampuan melakukan
usaha.
Jenis2 energi :
- mekanis (berkenaan dg posisi, struktur internal,
gerak)
- Kimiawi
- Listrik
- Termal
- Nuklir

11. Energi Potensial
E. Potensial : berkaitan dg struktur internal, posisi.
Contoh : pegas yang ditekan berkaitan dg
struktur internal, dpt mlakukan usaha mmpunyai
tenaga potensial.
to
m
spring at an equilibrium position
∆x
t m
spring compressed

12. Energi Potensial (lanjutan)
Contoh : benda pada suatu ketinggian.
(terkait dg posisi) dpt mlakukan usaha,
mempunyai tenaga potensial gravitasi.
Beda tenaga potensial gravitasi dari suatu
benda antara titik A dg titik A’ samadengan
m UA’ negatif dari usaha yang dilakukan oleh gaya
gravitasi untuk memindahkan benda tersebut
dari A ke A’.
UA : berpotensi minimum/kecil
m UA UA’ : berpotensi besar
h=0

13. Energi Potensial (lanjutan)
ΔUA’A = UA’ – UA = - WAA’
WAA’ = usaha yg dilakukan oleh gaya gravitasi bila benda
berpindah dari A ke A’.
= - mgΔh
Sehingga :
ΔUA’A = UA’ – UA = mgΔh.
Perjanjian : kasus di atas berlaku karena permukaan bumi/tanah
dianggap memiliki U = 0. Dapat pula dikatakan
tenaga potensial suatu benda yg berada pada ktinggian h
dari permukaan bumi adalah :
Uh = mgh.
Uh hanya bergantung pd lokasi benda, tdk bergantung pd
jalan / lintasan yg digunakan utk membawa benda tsb
hingga berada di ktinggian h.
Jadi, gaya gravitasi gaya konservatif

14. Tenaga Gerak / energi Kinetik
Bila gaya konstan F bekerja pada suatu massa m sehingga benda
tersebut bergeser sejauh Δx pada arah gaya tsb maka timbul
percepatan a =F/m yg akan mengubah kecepatan benda dari v0
menjadi va. Berlaku :
va2 = v0 2 + 2a Δx
= v0 2 + 2(F/m) Δx
Atau
FΔx = ½ m va2 - ½ m v02
FΔx : usaha yg telah dilakukan oleh gaya F untuk menggeser
benda sejauh Δx .
½ m va2 - ½ m v02 : perubahan besaran ½ mv2

15. Tenaga Gerak / energi Kinetik (lanjutan)
Jadi besaran K = ½ mv2
Dinamakan tenaga kinetik atau tenaga gerak dari massa m.
Jadi, W = Δ K (teorema usaha-tenaga kinetik)
artinya : usaha yg telah dilakukan atas massa m sama
dengan besarnya perubahan tenaga kinetik massa
tsb.
Ada 2 keadaan istimewa :
1. Bila W > 0 ( F searah dg arah pergeseran Δ x) maka Δ K
> 0, artinya ada kenaikan tenaga kinetiknya (va > v0 ).
2. Bia W < 0 ( F berlawanan arah dg arah pergeseran Δ x)
maka Δ K < 0, artinya ada penurunan tenaga kinetiknya
(va < v0 ).

16. Prinsip kekekalan Tenaga
v A’
Benda massa m berpindah dari A
ke A’.
UA m UA’ , K A’ di A : tenaga potensial = UA
tenaga kinetik = KA
h A’ di A’ : tenaga potensial = UA’
vA tenaga kinetik = KA’
m
UA, KA Usaha yg dilakukan :
hA WA A’ = KA’ – KA = ΔK
U=0 (teorema usaha-tenaga kinetik)
Dari definisi tenaga potensial :
ΔU = UA’ – UA = - W A A’ = - ΔK
Sehingga, ΔK + ΔU =0 atau KA’ + UA’ = KA + UA

17. Prinsip kekekalan Tenaga(lanjutan)
Artinya :
(K+U)akhir = (K+U)awal
K+U : tenaga mekanis = Em
Ksimpulan :
untuk gaya-gaya konservatif berlaku
prinsip kekekalan tenaga mekanis
Em = K + U

18. Apakah prinsip kekealan Em terpengaruh oleh
pemilihan / penetapan tempat U =0 ?
Contoh : benda bermassa m dilempar ke atas dan berhenti pada
ketinggian h dari permukan tanah.
v= 0 v= 0
U = mgh U=0
h h
vA vb
m m
U=0 U = -mgh
(a) (b)

19. Kalau pemilihan U = 0 tidak mempengaruhi prinsip
kekekalan tenaga mekanis maka harus dapat dibuktikan
bahwa va = vb !
Menurut gambar (a) :
(K+U)awal = ½ mva2 ; (K+U)akhir = mgh
(K+U)akhir = (K+U)awal
½ mva2 = mgh
Va = 2 gh
Menurut gambar (b) :
(K+U)awal = ½ mvb2 - mgh ; (K+U)akhir = 0
(K+U)awal = (K+U)akhir
½ mvb2 - mgh = 0
Vb = 2 gh

20. Tinjauan secara umum
(K+U)awal = ½ mvc2 – mgh1
(K+U)akhir = 0 + mgh2
U = mgh2
(K+U)awal = (K+U)akhir
v= 0
½ mvc2 – mgh1 = mgh2
h2
U=0 Vc = 2 g (h1 + h2 )
h
Vc = 2 gh
h1
vc
m U = -mgh1
(c)

21. Daya
• Daya sesaat adalah dW
P=
dt
• Satuan Daya P = satuan tenaga/satuan waktu
Watt = joule / sekon
1 kWh = 1 kilowattjam = 103 watt (3600 sekon) = 3,6 x 106 Ws
= 3,6 x 106 J
Untuk gaya konstan W = F ∆x = F (v0 t + ½ at2)
Sehingga P = dW/dt = F (v0 + at)