Dokumen ini adalah ringkasan materi kalkulus kelas XII yang mencakup pengertian integral, baik tertentu maupun tak tertentu, serta penerapan dan rumus-rumus terkait. Terdapat juga rumus integral untuk fungsi trigonometri dan latihan soal untuk memahami konsep-konsep tersebut. Semua topik ditujukan untuk memberikan pemahaman mendalam tentang pengintegralan dalam matematika.

![RUMUS-RUMUS INTEGRAL FUNGSI TRIGONOMETRI
09. ∫ sec2 (ax + b) dx = 1/a tan (ax + b) + C
01. ∫ cos x dx = sin x + C
10. ∫ cosec2 (ax + b) dx = -1/a cot (ax + b) + C
02. ∫ sin x dx = -cos x + C
11. ∫ tan (ax + b)sec (ax + b) dx = 1/a sec (ax + b) + C
03. ∫ Sec2 x dx = tan x + C
12. ∫ cot (ax + b) cosec (ax + b ) dx = -1/a cosec (ax + b) +
04. ∫ cosec2 x dx = -cot x + C
C
05. ∫ tanx sec x dx = sec x + C 13. ∫ tan x dx = ln | sec x | + C
06. ∫ cot x . cosec x dx = -cosec x + C 14. ∫ cot x dx = ln | sin x | + C
07. ∫ cos (ax + b) dx = 1/a sin (ax + b) + C
15. ∫ sec x dx = ln | sec x + tan x | + C
08. ∫ sin (ax + b) dx = -1/a cos (ax + b) +
C 16. ∫ cosec x dx = ln | cosec x -cot x| + C
Rumus-rumus trigonometri yang diperlukan dalam pengintegralan
01. sin2 A + cos2A = 1 06. cos2A = 1 ( 1 + cos 2A )
2
02. tan2A + 1 = sec2 A 07. sin A cos B = 1 [ sin (A + B) + sin (A – B) ]
2
03. cot2A + 1 = cs c2 A 08. cos A sin B = 1 [ sin (A + B) – sin (A – B) ]
2
04. sin A cos A = 1 sin 2A 09. cos A cos B = 1 [ cos (A + B) + cos (A – B) ]
2 2
05. sin2A = 1 ( 1 – cos 2A ) 10. sin A sin B = – 1 [ cos (A + B) – cos (A – B) ]
2 2
LATIHAN SOAL
∫ (3X − 6X + 7) dx = .... 1
2
1. 2. ∫ 2x x
dx =
A. 6 x3 − 6x2 + 6x + C
1 2
B. x3 − 3x2 + 7x + C A. − +C D. +C
C. 3x3 − 6x2 + 7x + C x x
2x3 − 5x2 + 6x + C 2 1
D. B. − +C E. − +C
E. 1 x3 − 5x2 + 7x + C x 2 x
3
1
C. +C
x
3](https://image.slidesharecdn.com/kalkulusxii1-120322025135-phpapp02/85/Kalkulus-xii-1-3-320.jpg)

![17. Luas daerah bidang yang dibatasi oleh 25. Luas daerah yang y
kurva y = x2, sumbu x, garis x = 1 dan x = 3 dibatasi oleh parabola
adalah dan sumbu x, seperti
A. 46/3 D. 16/3 pada gambar, adalah
B. 36/3 E. 6/3 32. Ordinat puncak
C. 26/3 parabola adalah x
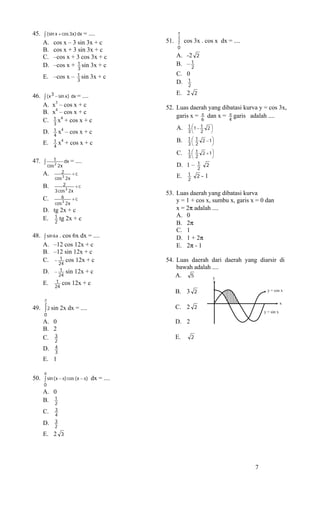
0 (4, 0)
A. 4
18. Luas bidang yang dibatasi oleh parabola B. 8
x = 8 + 2y - y2 sumbu y, garis y = -1 dan C. 12
y = 3 adalah D. 16
A. 42/3 D. 82/3 E. 18
B. 52/3 E. 92/3
C. 62/3 26. Daerah yang dibatasi oleh kurva : y2 = 10x,
y2 = 4x dan x = 4 diputar 360o mengelilingi
19. Luas daerah yang dibatasi parabola : sumbu x. Volume benda putar yang terjadi
y = x2 - 7x + 6, sumbu x dan garis-garis adalah
x = 2 dan x = 6 adalah
A. 80 π satuan D. 24 π satuan
A. 56/3 D. 26/3
B. 46/3 E. 16/3 B. 48 π satuan E. 18 π satuan
C. 36/3 C. 32 π satuan
20. Luas daerah yang dibatasi oleh kurva 27. Daerah yang dibatasi oleh kurva y = 4x - 2,
y = x3 - 6x2 + 8x dan sumbu x adalah sumbu X, x = 1 dan x = 3 diputar
A. 4 D. 7 mengelilingi sumbu X sejauh 360o. Volume
B. 5 E. 8 benda putar tersebut adalah
C. 6 A. 35 1/3 π D. 82 2/3 π
B. 40 2/3 π E. 83 1/3 π
21. Luas daerah yang dibatasi oleh kurva C. 45 1/3 π
y = 6x - x2 dan y = x2 - 2x pada interval
[1, 4] adalah 28. Daerah D terletak di kuadran pertama yang
A. 14 2/3 D. 18 dibatasi oleh parabola y = x2, parabola
B. 16 E. 24 y = 4x2 dan garis y = 4. Volume benda
C. 16 2/3 putar yang terjadi bila D diputar terhadap
sumbu y adalah ....
22. Luas daerah yang dibatasi oleh parabola: A. 3π D. 8π
y = 6x - x2 dan y = x2 - 2x adalah B. 4π E. 20π
A. 32/3 D. 72/3 C. 6π
B. 42/3 E. 82/3
C. 64/3 29. Daerah yang dibatasi oleh kurva y2 = x + 2,
y2 = 2x dan sumbu x diputar mengelilingi
23. Luas daerah antara kurva y = x2 + 4x + 7 sumbu x sejauh 360o, sehingga diperoleh
dan y = 13 - x2 adalah sebuah benda putar. Volume benda putar itu
A. 10 2/3 D. 32 2/3 adalah ....
B. 14 2/3 E. 39 1/3 A. 2π D. 5π
C. 21 1/3 B. 3π E. 6π
C. 4π
24. Perhatikan gambar di bawah ini ! x2 y2
Luas daerah yang diarsir adalah 30. Daerah yang dibatasi oleh elips + =1
a2 b2
A. 1/12 satuan luas dan subu x yang berada di kuadran pertama
17 diputar mengelilingi sumbu x satu putaran.
B. /12 satuan luas Volume benda putar yang terjadi adalah ....
9 A. 2/3 ab2π D. 4/3 a2 bπ
C. /4 satuan luas
B. 4/3 ab π
2
E. 4/3 a2 b2π
D. 8
/3 satuan luas C. 2/3 a2 bπ
37
E. /12 satuan luas
5](https://image.slidesharecdn.com/kalkulusxii1-120322025135-phpapp02/85/Kalkulus-xii-1-5-320.jpg)