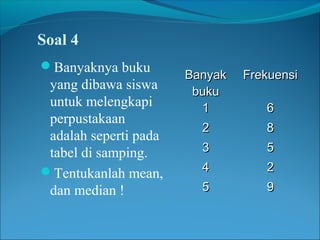
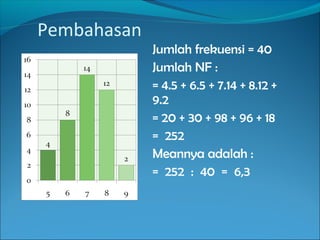
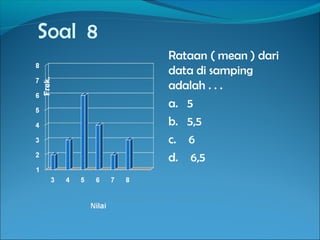
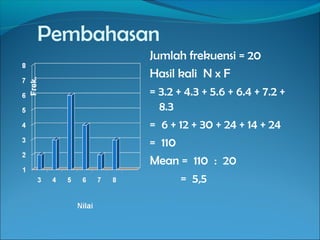
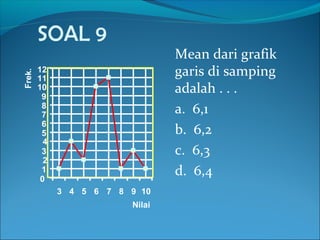
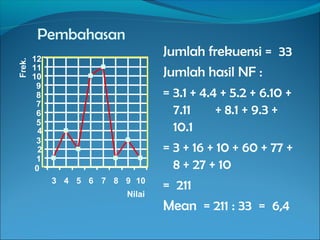
Dokumen ini menjelaskan tentang pemusatan data yang mencakup pengertian mean, median, dan modus serta rumus-rumus untuk menghitungnya. Terdapat contoh-contoh soal yang menunjukkan cara menentukan rata-rata, median, dan modus dari sekumpulan data. Informasi juga mencakup pembahasan penerapan rumus tersebut dalam berbagai situasi pendidikan.

2. MATERI
Pemusatan data terdiri dari :
Mean ( Nilai rata-rata )
Modus ( Nilai frekuensi tertinggi)
Median ( Nilai tengah dari data )
Jangkauan/rentangan suatu data

3. MEAN ( RATA-RATA)
Mean atau rata-rata hitung dari
sekumpulan data adalah jumlah
data-data itu dibagi banyaknya
data, dilambangkan dengan x

4. RUMUS MEAN
Pada umumnya untuk menentukan
rata-rata hitung dari n buah data x1,
x2, x3, …, xn adalah :
x1 + x2 + x 3 + … + x n
x =
n

5. Contoh 1
Dari sekelompok siswa Nilai Frekuensi
sebanyak 30 orang
5 1
memperoleh nilai
ulangan matematika 6 5
seperti tabel frekuensi 7 10
di samping. Tentukan
rata-rata hitungnya! 8 7
9 4
10 3

6. Pembahasan
5.1 + 6.5 + 7.10 + 8.7 + 9.4 + 10.3
x =
1 + 5 + 10 + 7 + 4 + 3
227
x =
30
x = 7,6

7. MEDIAN ( Me )
Median merupakan nilai tengah dari
sekumpulan data setelah data itu
diurutkan.
Bila banyaknya data ganjil, maka
median akan diperoleh tepat di
tengah-tengah kelompok.

8. MEDIAN ( Me )
Bila banyaknya data genap, maka
median akan diperoleh dari setengah
jumlah dua bilangan yang berada di
tengah setelah data diurutkan.

9. RUMUS MEDIAN
Jumlah n + 1
Me =
data ganjil 2
Jumlah n n+1
Me = ½ +
data genap 2 2

10. Contoh 1
Tentukanlah median dari data
berikut !
a. 12, 11, 15, 13, 14, 14, 10,
16, 13.
b. 60, 25, 50, 80, 75, 20, 80,
40, 70, 50, 25, 75.

11. Pembahasan :
a. Jumlah data 9 atau ganjil, maka
mediannya data tengah setelah
diurutkan.
10, 11, 12, 13, 13, 14, 14, 15, 16
Jadi, median dari kelompok data itu
adalah 13.

12. b. Jumlah data 12 atau genap, maka median
nya terletak pada data n/2 dan data n + 1/2 setelah
diurutkan.
n n+1
Me = ½ ,
2 2
20, 25, 25, 40, 50, 50, 60, 70, 75, 75, 80,80
Median data tersebut : ½ ( 50 + 60 ) = 55

13. MODUS
Modus dari sekumpulan data
mungkin ada satu, dua, atau lebih,
jika pada data tersebut jumlah data
yang sering muncul ada yang sama.

14. Contoh 1
Tentukanlah modus dari data berikut !
a. 6, 9, 9, 7, 8, 3, 4, 6, 5, 9, 8
b. 22, 26,25, 24, 23, 25, 27, 26, 28

15. Pembahasan :
a. Nilai yang frekuensinya paling banyak
adalah 9, yaitu muncul 3 kali.
Jadi, modusnya adalah 9.
b. Data yang paling sering muncul adalah 25
dan 26 masing-masing dua kali.
Jadi, modusnya adalah 25 dan 26.

17. Soal 1
Data 5 6 7 8 9
Frekuensi 4 8 14 12 2
Tentukanlah modus dari data dalam
tabel di atas !

18. Pembahasan
Modus dari data tabel adalah nilai yang
mempunyai frekuensi paling besar/
tertinggi atau data yang paling sering
muncul.
Nilai 7 dengan frekuensi 14.
Jadi, modusnya adalah 7,0

19. Soal 2
Data 5 6 7 8 9
Frekuensi 4 8 14 12 2
Tentukan mean atau nilai rata-rata
hitung dari data dalam tabel di atas !

20. Pembahasan
N F NxF Nilai mean (rataan) dari
5 4 20 data tersebut di atas
6 8 48 adalah :
7 14 98
Mean = ∑NxF : ∑F
8 12 96
9 2 18 = 280 : 40
∑ 40 280
= 7,0

21. Soal 3
Dari 12 mata pelajaran di kelas II pada
buku laporan seorang siswa mendapat
nilai sebagai berikut :
7 6 8 9 8 7 8 6 7 9 7 6
Tentukanlah mean, median, dan modus
dari nilai diatas!

22. Pembahasan
Data nilai :
7 6 8 9 8 7 8 6 7 9 7 6
Mean = ( 88 : 12 ) = 7,33
diurutkan :
6 6 6 7 7 7 7 8 8 8 9 9
Median = ½ ( dt. 6 + dt. 7 )
= ½( 7 + 7 ) = 7

23. Pembahasan
Data nilai :
7 6 8 9 8 7 8 6 7 9 7 6
diurutkan :
6 6 6 7 7 7 7 8 8 8 9 9
Modus data tersebut adalah 7,
karena nilai 7 frekuensinya = 4.

24. Soal 4
Banyaknya buku
Banyak Frekuensi
yang dibawa siswa buku
untuk melengkapi 1 6
perpustakaan
2 8
adalah seperti pada
tabel di samping. 3 5
Tentukanlah mean, 4 2
dan median ! 5 9

25. Pembahasan
Tentukan jumlah
N F N.F
frekuensi dan jumlah
hasil kali NF. 1 6 6
Mean = 90 : 30 = 3 2 8 16
Jadi mean adalah 3 3 5 15
Median adalah dt. 15 4 2 8
( 3 ) dan dt. 16 ( 3 ) 5 9 45
Jml 30 90
Median = ½ ( 3 + 3 ) = 3

26. Soal 5
Nilai rata-rata hasil ulangan
matematika dari 40 siswa adalah 6.
Jika anak ke-41 mendapat nilai 7,
berapa nilai rata-rata ke-41 siswa
itu?

27. Pembahasan
Rata-rata nilai 40 anak = 6
Nilai anak ke-41 = 7
Rata-rata nilai ke-41 anak :
Mean = ( 40 x 6 + 7 ) : 41
= 247 : 41
= 6,024
= 6,02

28. SOAL 6
Mean dari data
grafik batang di
samping adalah . . .
a. 6,0
b. 6,2
c. 6,3
d. 6,4
Nilai

29. Pembahasan
Jumlah frekuensi = 40
Jumlah NF :
= 4.5 + 6.5 + 7.14 + 8.12 +
9.2
= 20 + 30 + 98 + 96 + 18
= 252
Meannya adalah :
= 252 : 40 = 6,3

30. SOAL 7
Berdasarkan diagram di
samping, rata-rata
produksi gula dari tahun
1990 sampai dengan 1995
adalah . . .
a. 400 ton
b. 450 ton
c. 550 ton
d. 600 ton

31. Pembahasan
Jumlah produksi gula
pada 1990 s.d 1995 :
= 300 + 400 + 350 + 500 +
450 + 400
= 2400 ton
Rata-rata = 2400 : 6
= 400 ton
Rata-rata produksi
selama 6 tahun = 400 ton

32. Soal 8
Rataan ( mean ) dari
data di samping
Frek.
adalah . . .
a. 5
b. 5,5
c. 6
d. 6,5

33. Pembahasan
Jumlah frekuensi = 20
Hasil kali N x F
Frek.
= 3.2 + 4.3 + 5.6 + 6.4 + 7.2 +
8.3
= 6 + 12 + 30 + 24 + 14 + 24
= 110
Mean = 110 : 20
= 5,5

34. SOAL 9
Mean dari grafik
12 garis di samping
Frek.
11
10
9
adalah . . .
8
7
a. 6,1
6
5 b. 6,2
4
3 c. 6,3
2
1
0
d. 6,4
3 4 5 6 7 8 9 10
Nilai

35. Pembahasan
12
Jumlah frekuensi = 33
Frek.
11
10 Jumlah hasil NF :
9
8 = 3.1 + 4.4 + 5.2 + 6.10 +
7
6 7.11 + 8.1 + 9.3 +
5
4 10.1
3
2 = 3 + 16 + 10 + 60 + 77 +
1
0 8 + 27 + 10
3 4 5 6 7 8 9 10
= 211
Nilai
Mean = 211 : 33 = 6,4