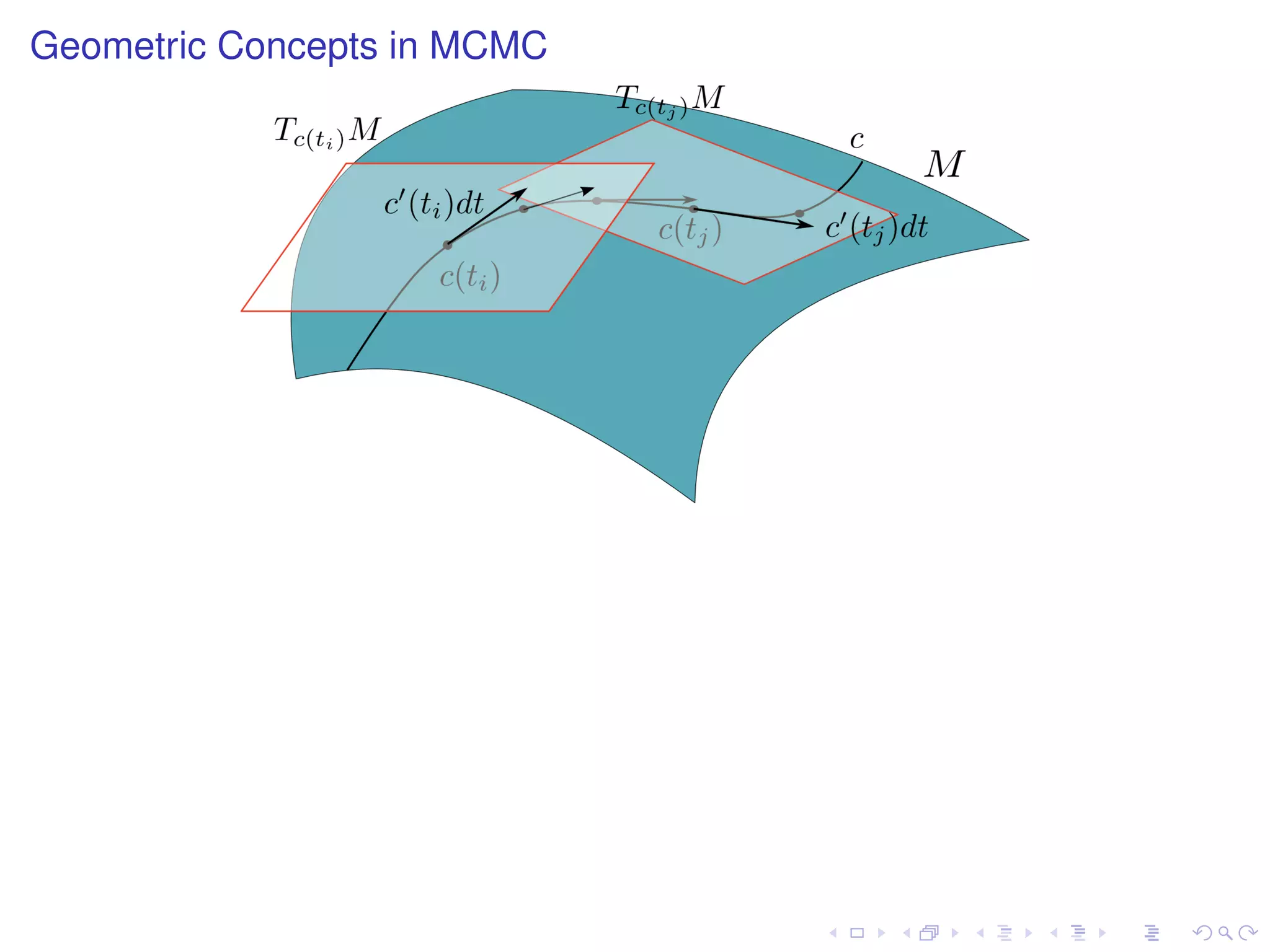
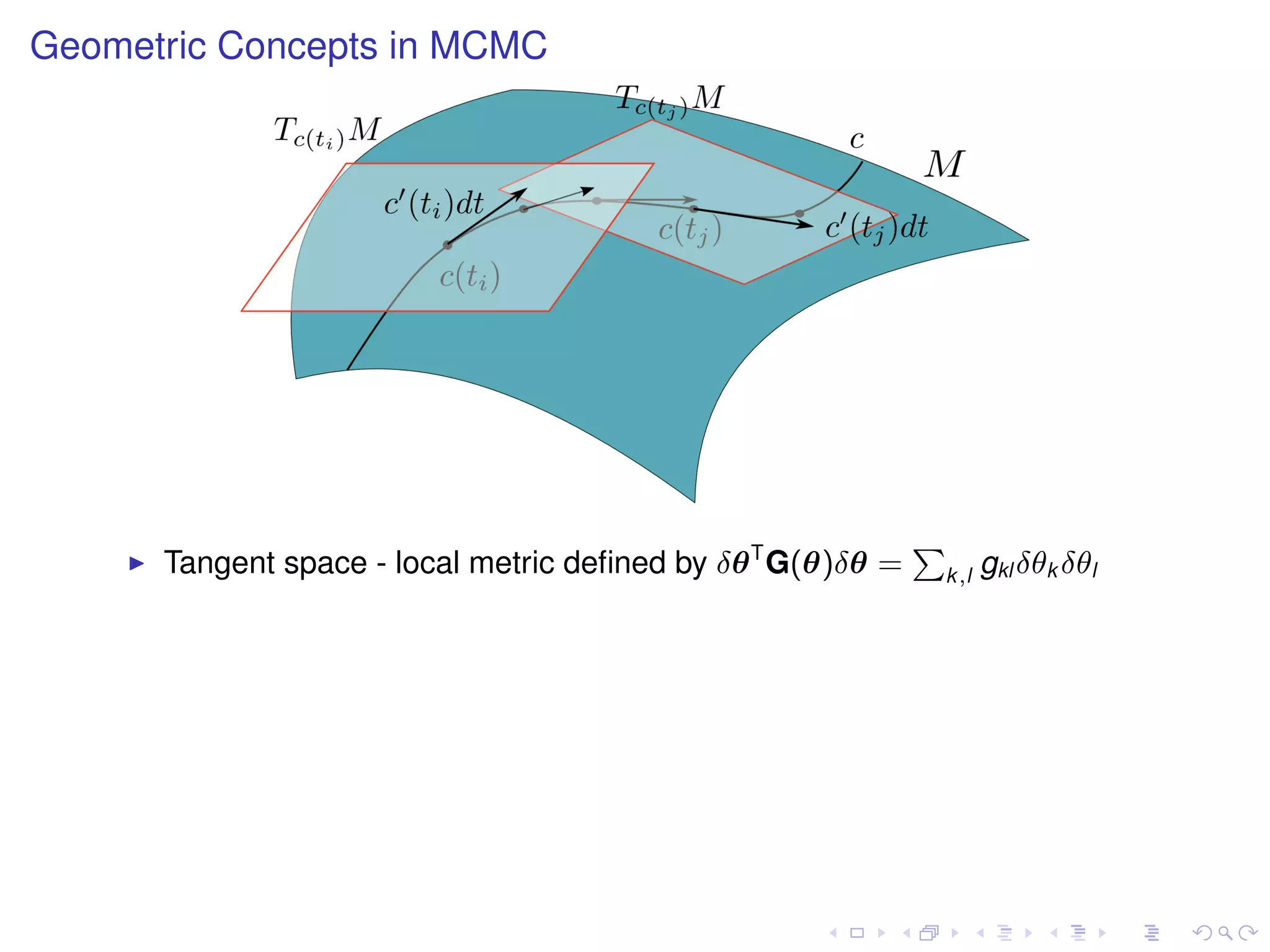
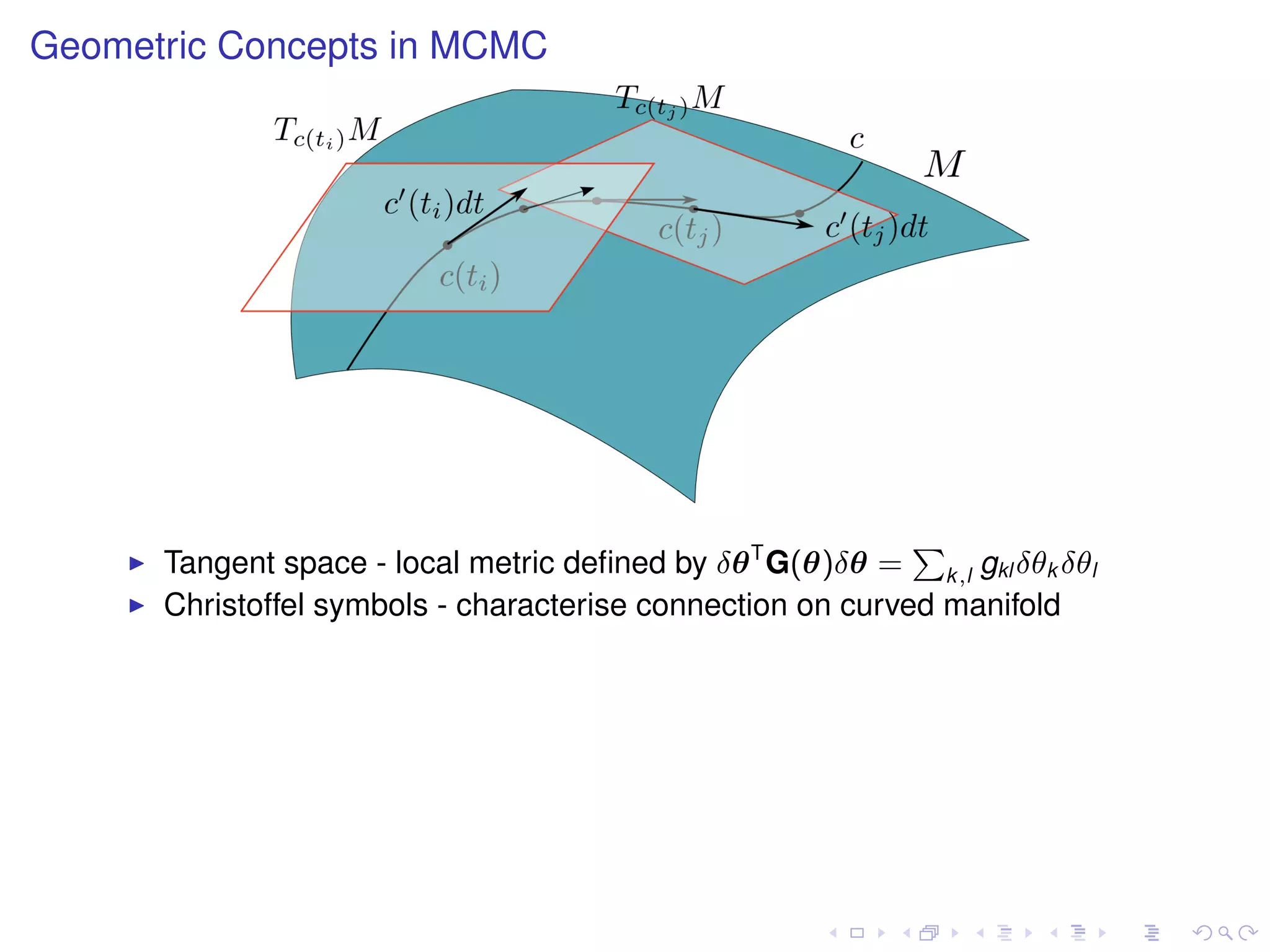
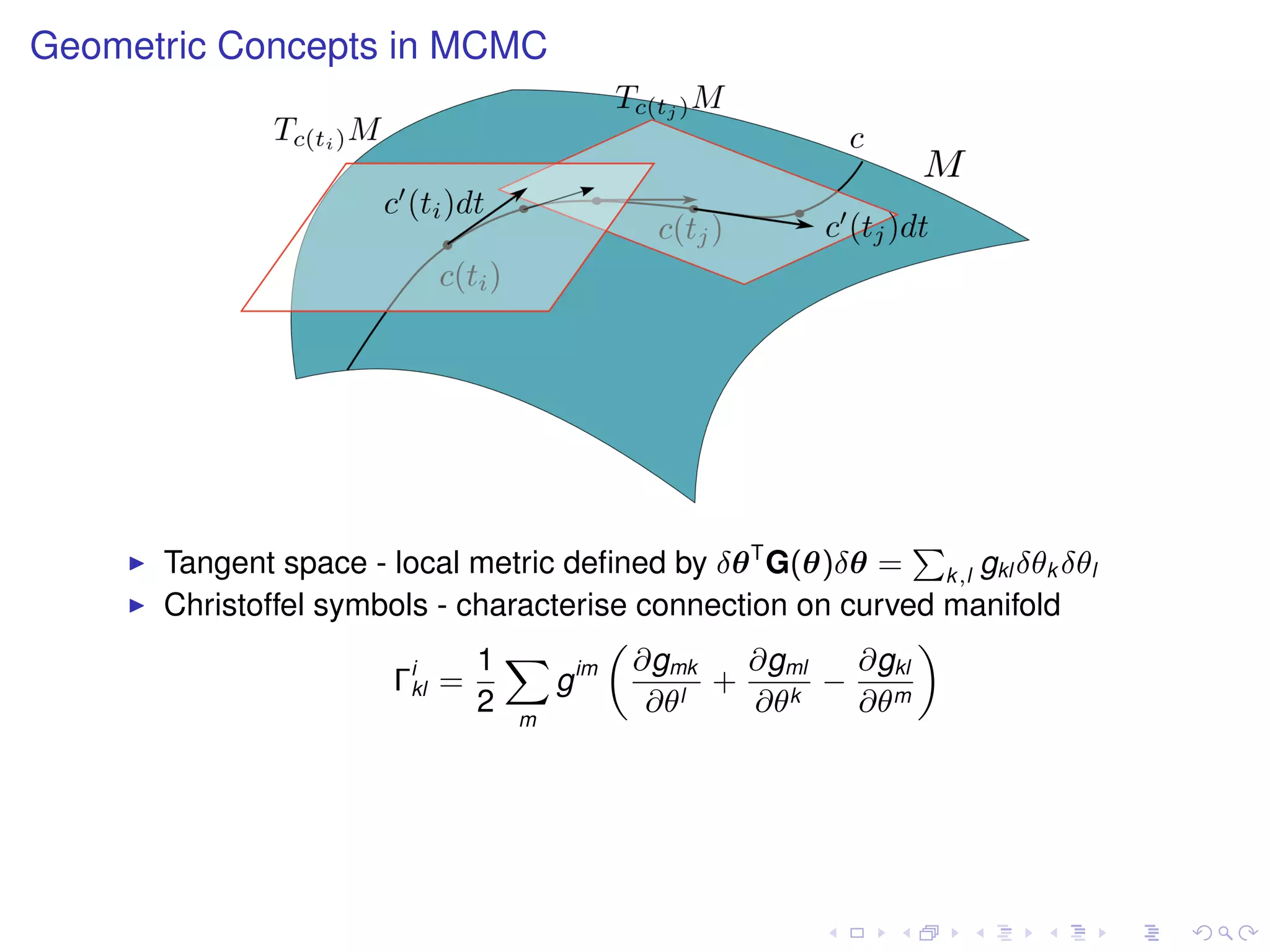
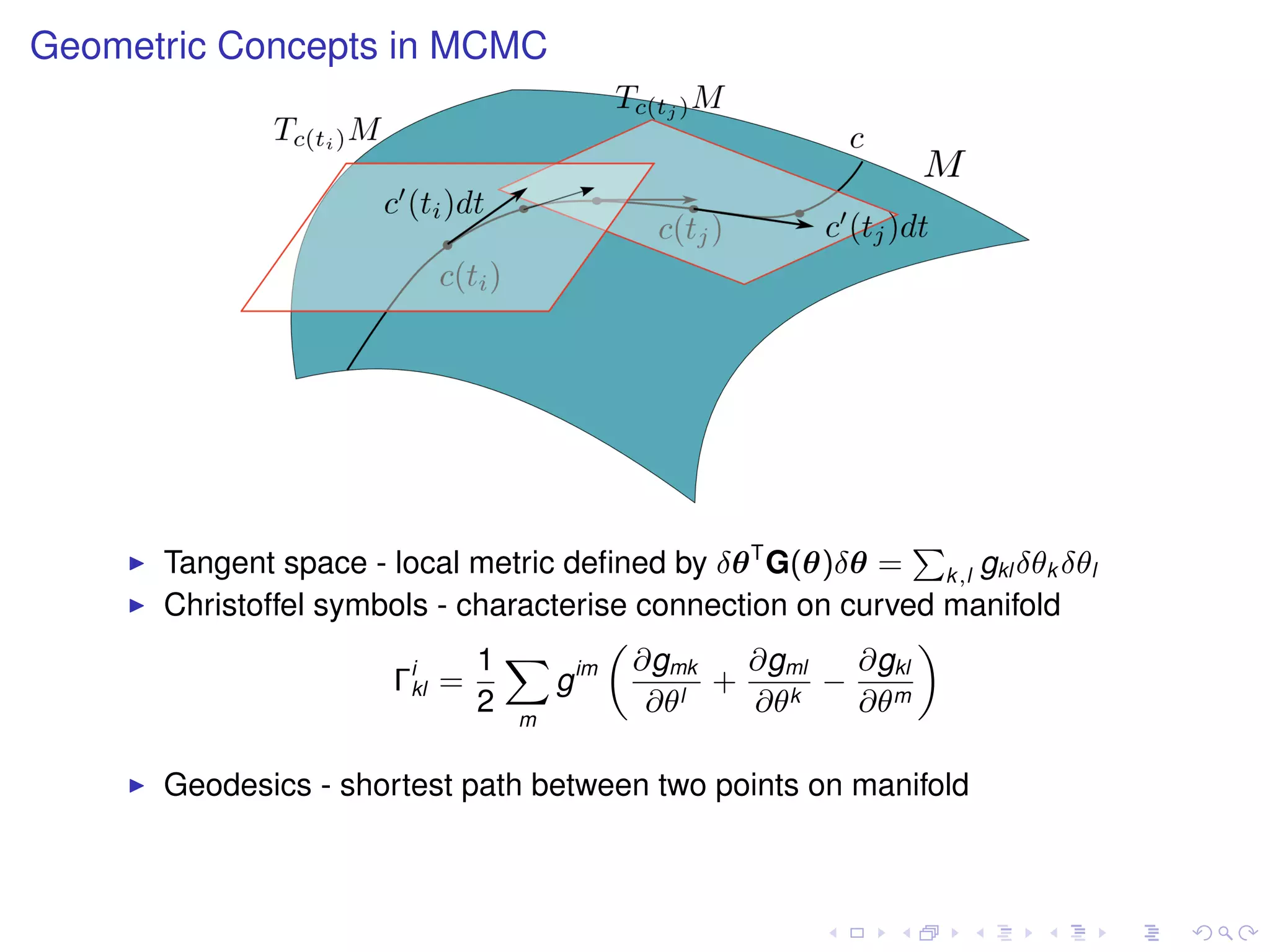
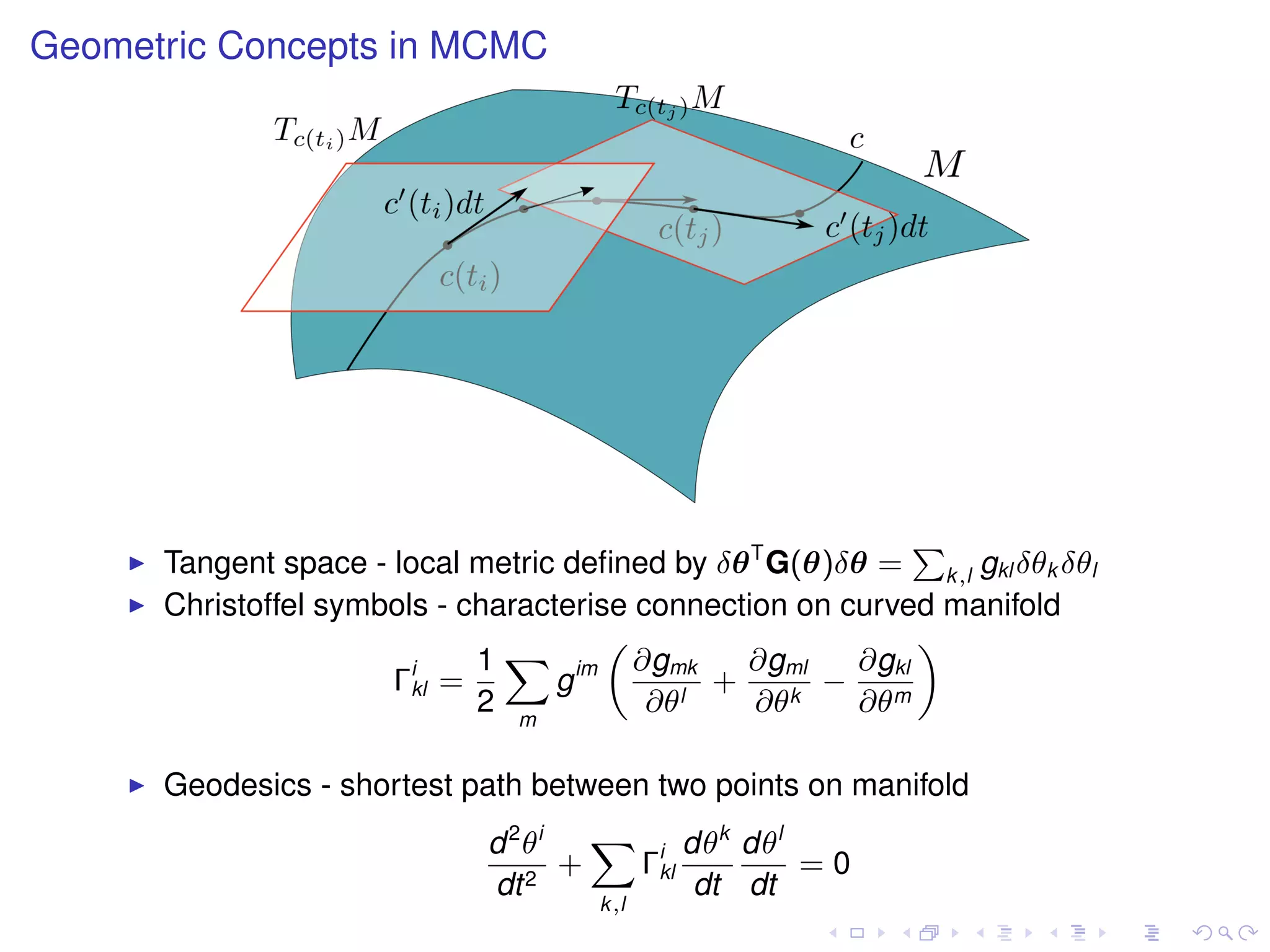
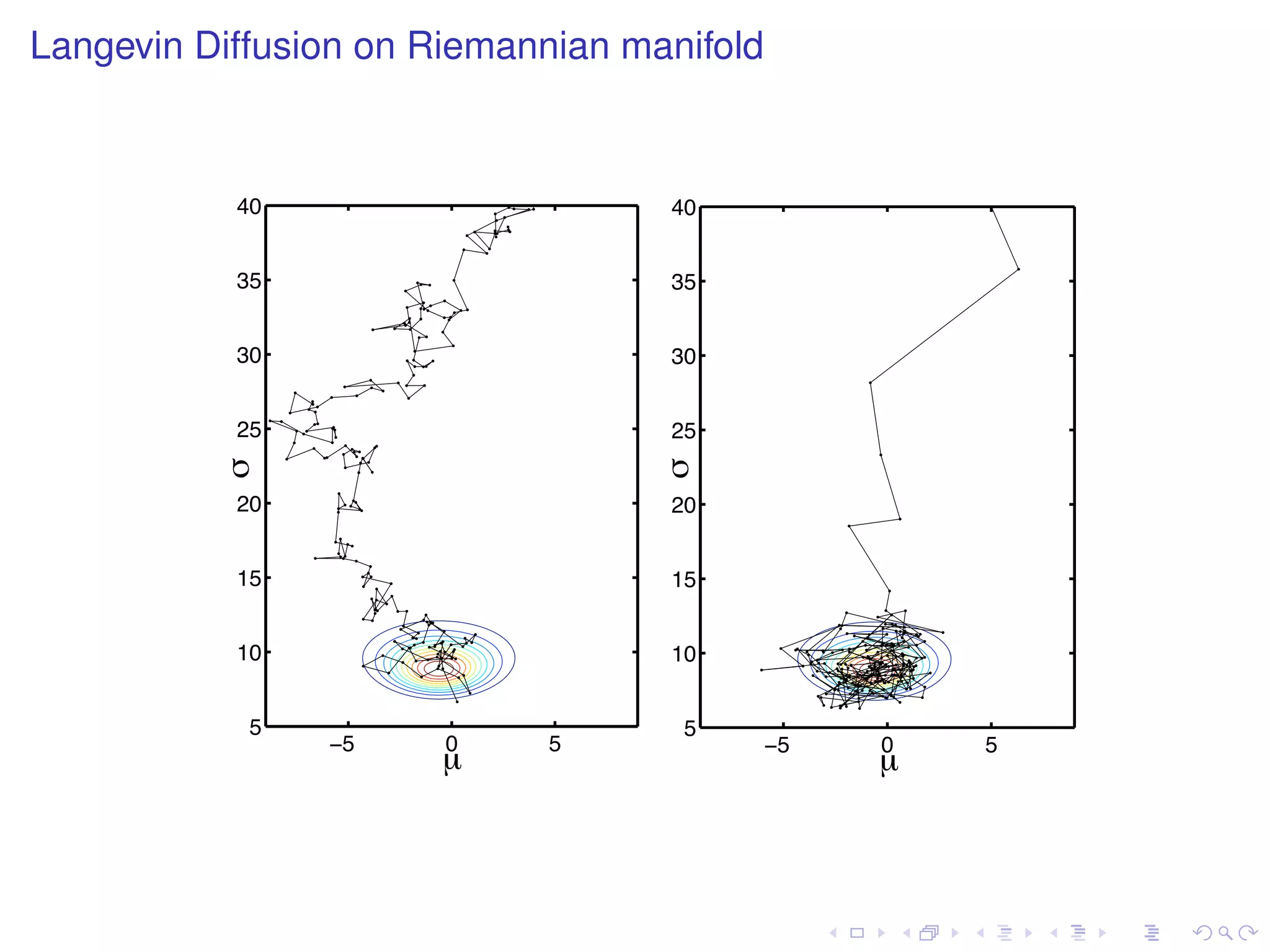
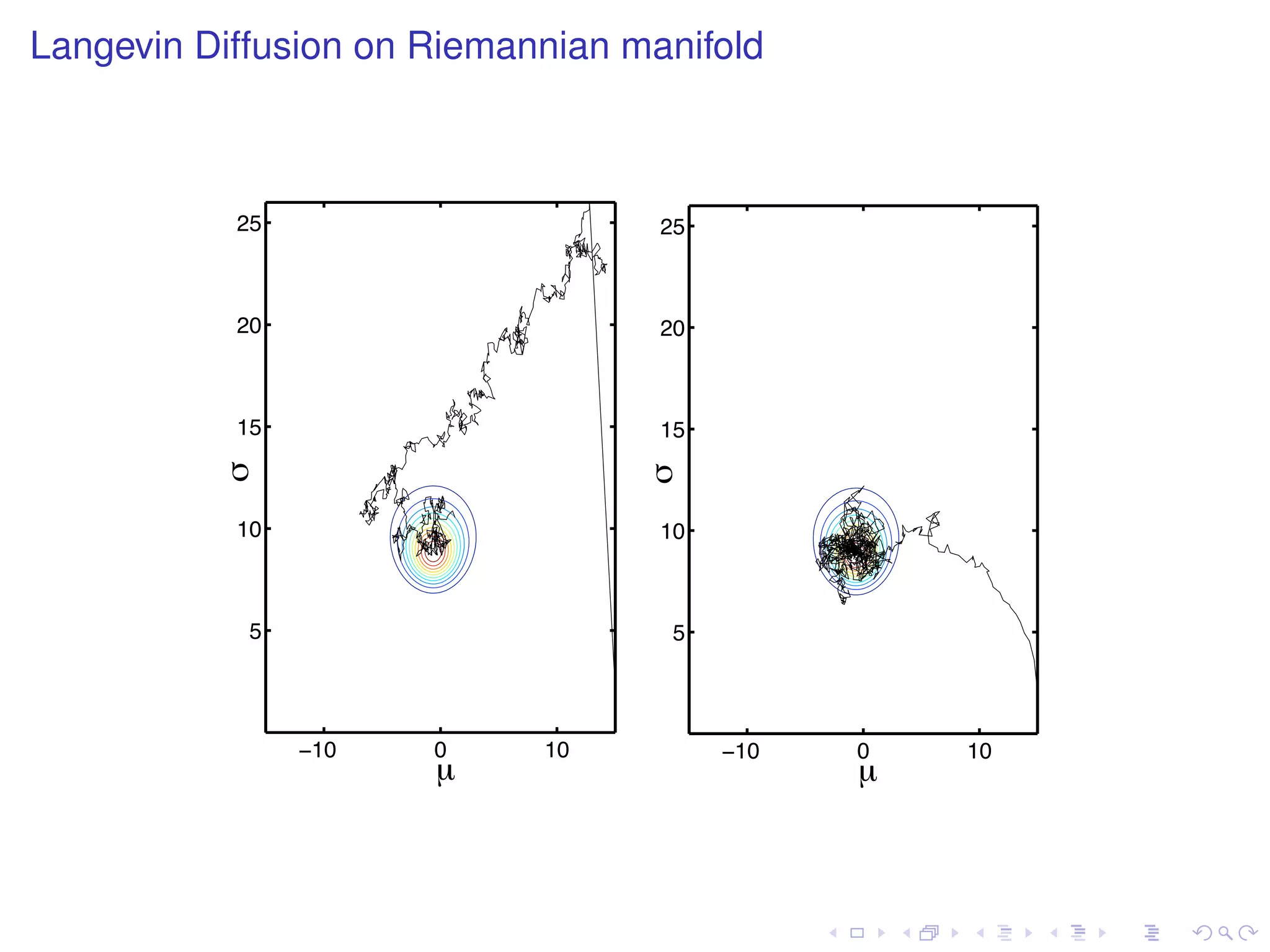
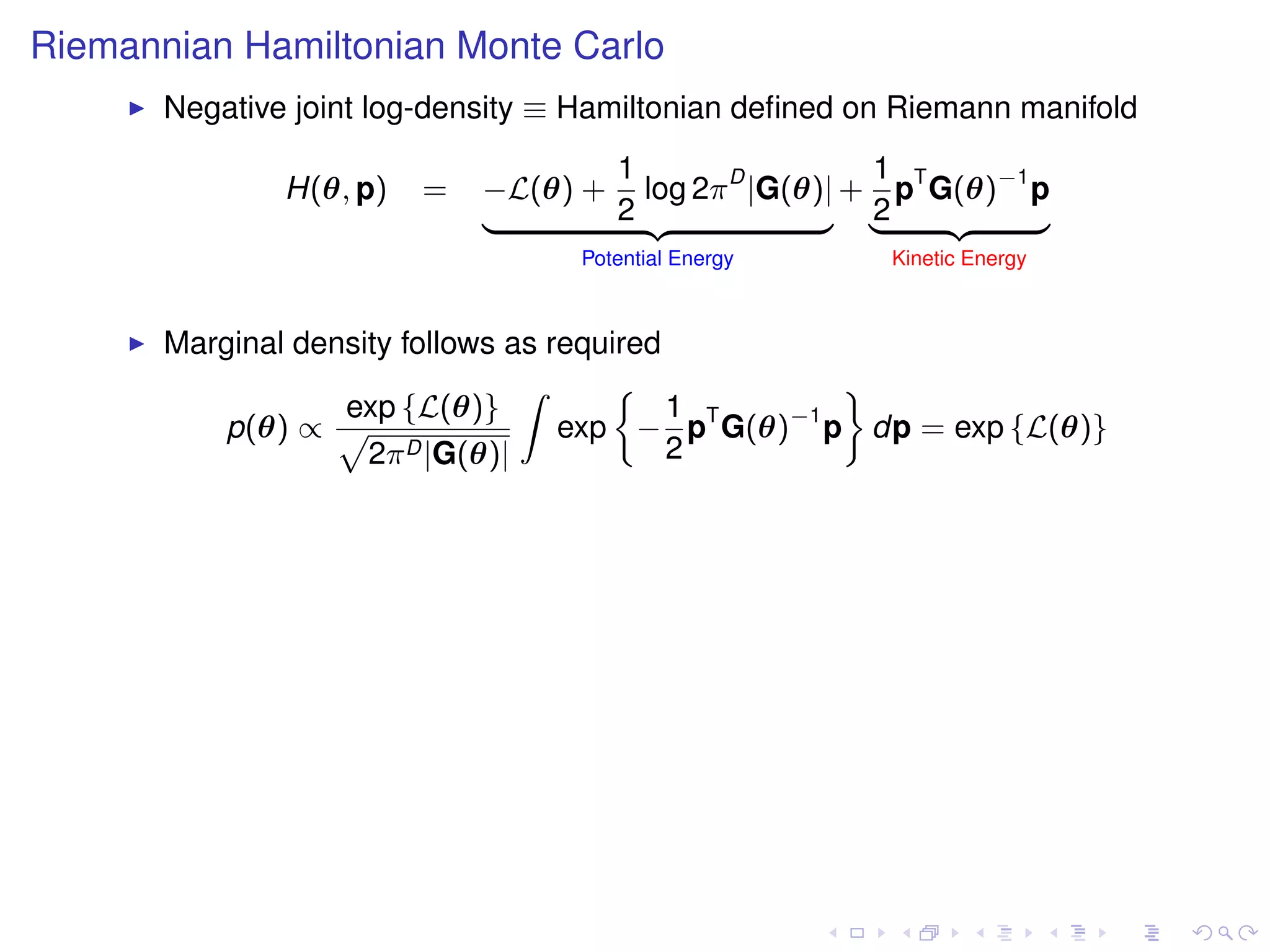
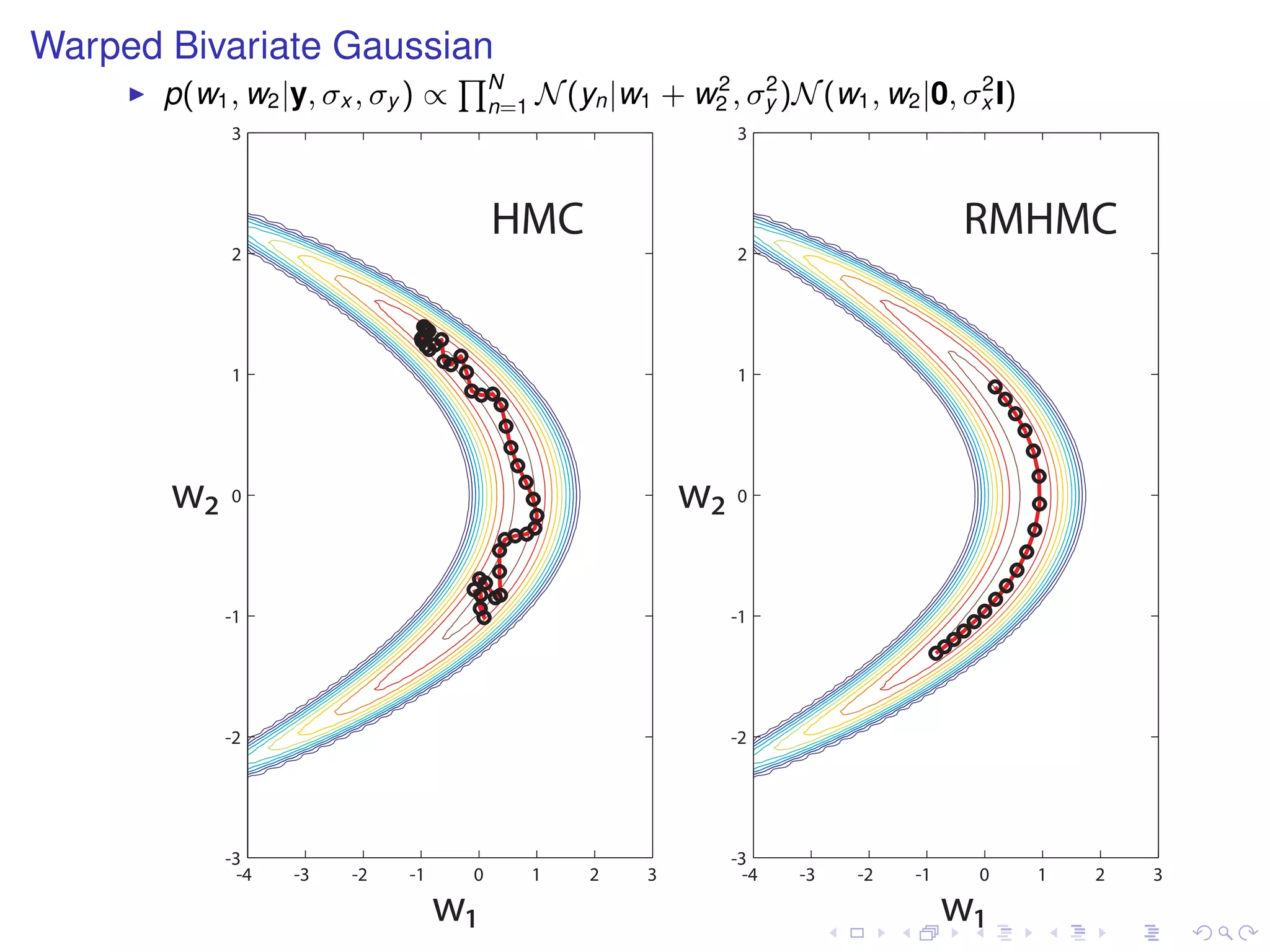
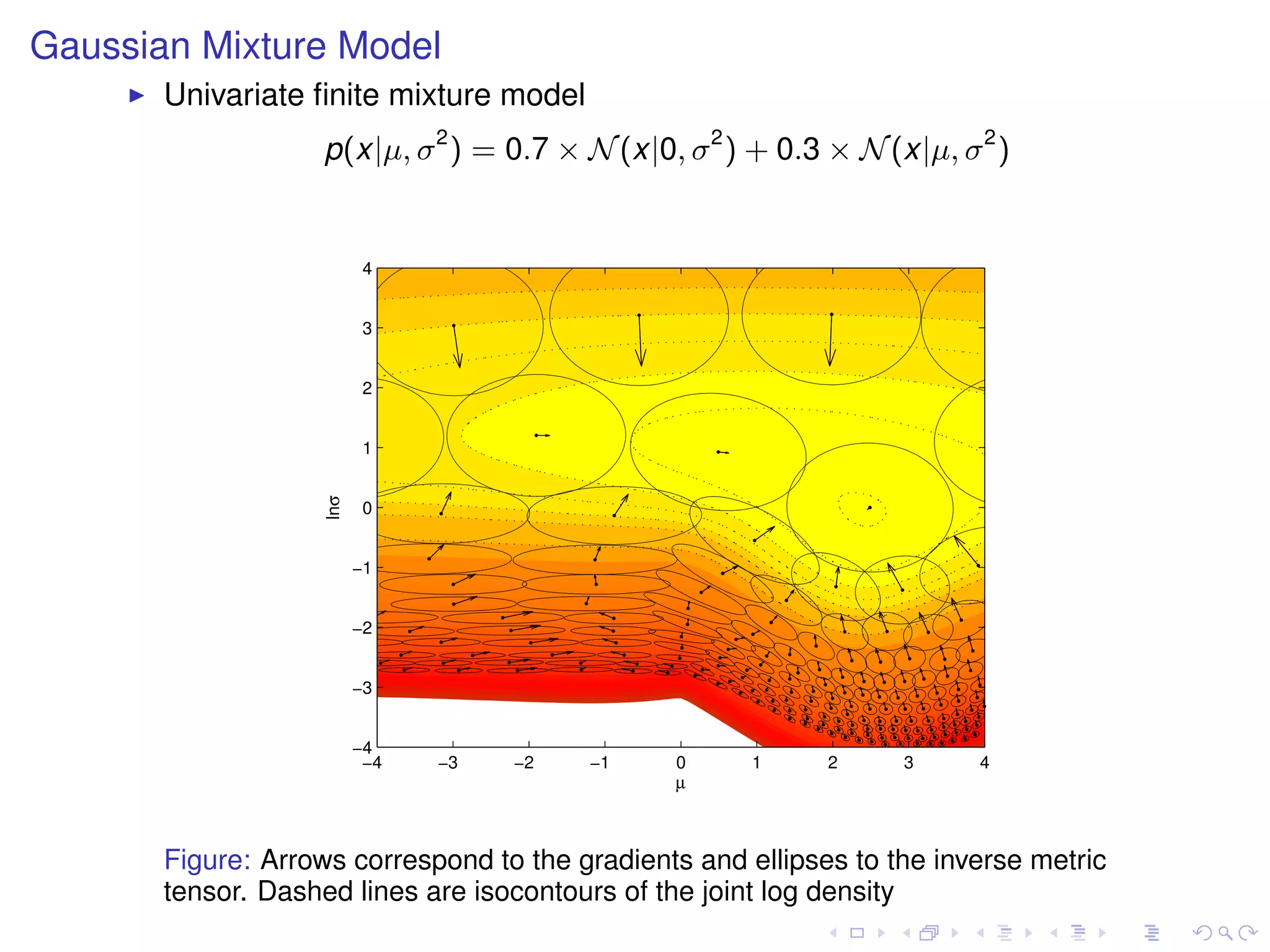
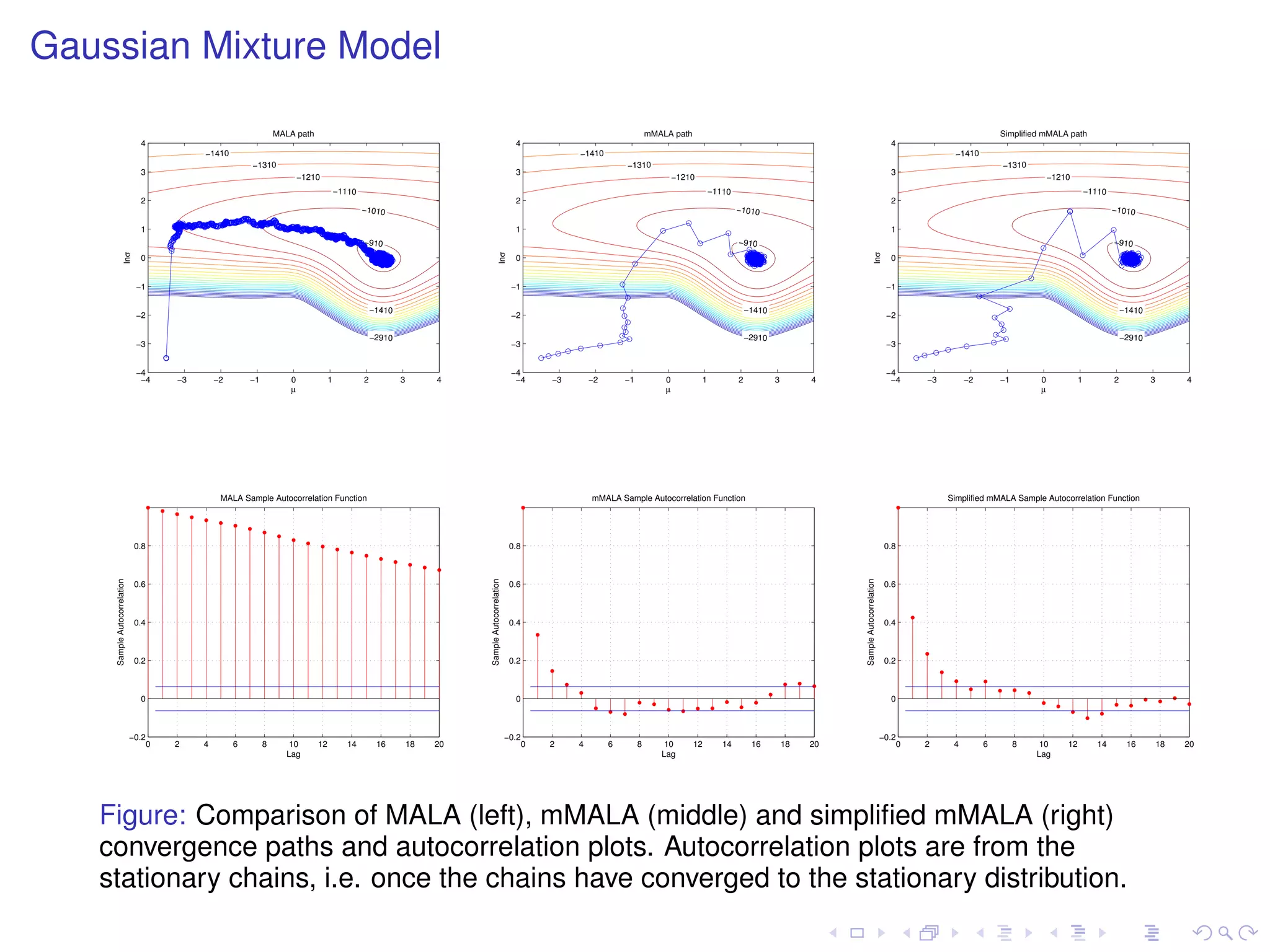
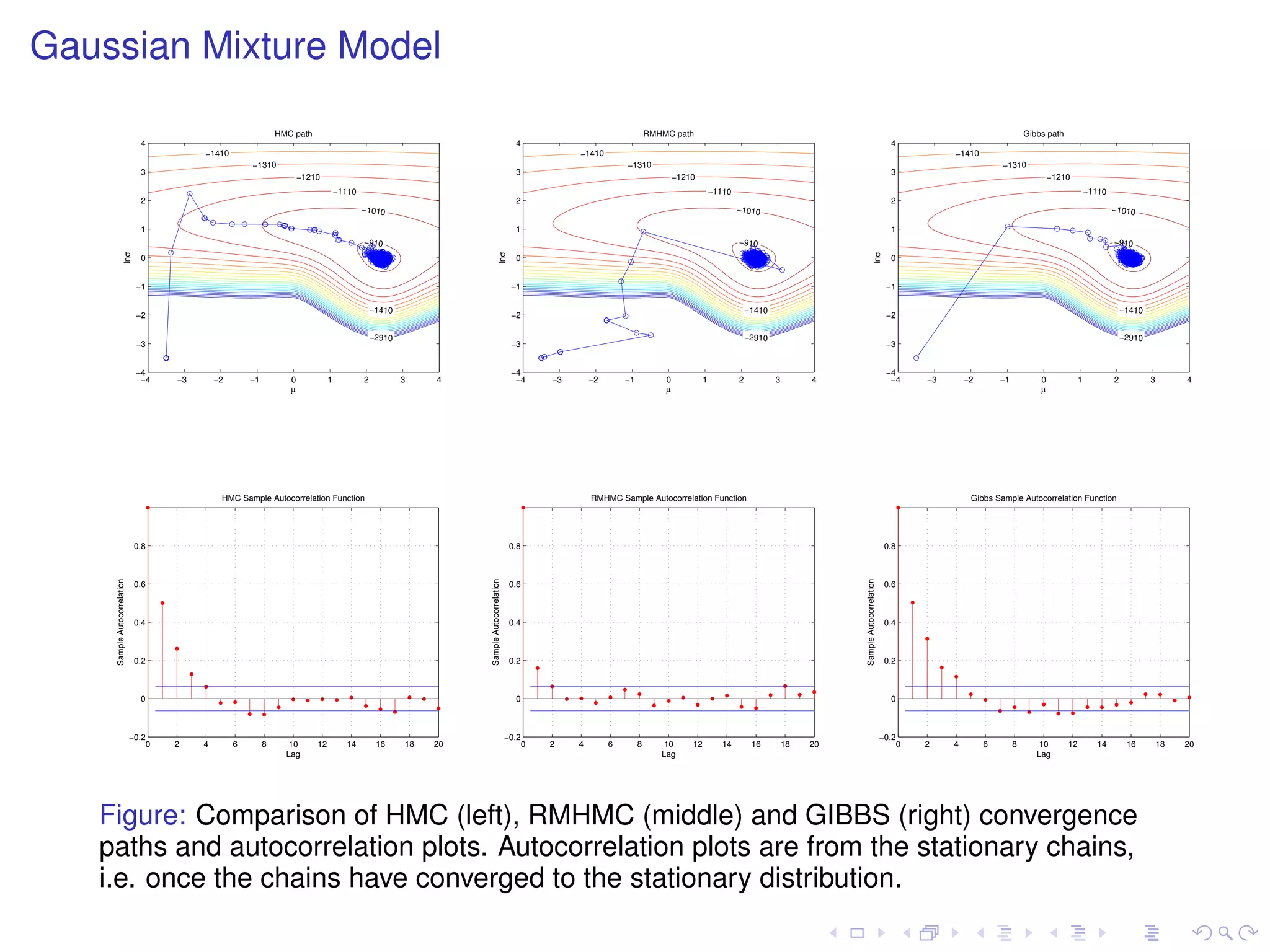
The document summarizes a talk given by Mark Girolami on manifold Monte Carlo methods. It discusses using stochastic diffusions and geometric concepts to improve MCMC methods. Specifically, it proposes using discretized Langevin and Hamiltonian diffusions across a Riemann manifold as an adaptive proposal mechanism. This is founded on deterministic geodesic flows on the manifold. Examples presented include a warped bivariate Gaussian, Gaussian mixture model, and log-Gaussian Cox process.

1. Manifold Monte Carlo Methods
Mark Girolami
Department of Statistical Science
University College London
Joint work with Ben Calderhead
Research Section Ordinary Meeting
The Royal Statistical Society
October 13, 2010

2. Riemann manifold Langevin and Hamiltonian Monte Carlo Methods

3. Riemann manifold Langevin and Hamiltonian Monte Carlo Methods

4. Riemann manifold Langevin and Hamiltonian Monte Carlo Methods
Riemann manifold Langevin and Hamiltonian Monte Carlo Methods
Girolami, M. & Calderhead, B., J.R.Statist. Soc. B (2011), 73, 2, 1 - 37.

5. Riemann manifold Langevin and Hamiltonian Monte Carlo Methods
Riemann manifold Langevin and Hamiltonian Monte Carlo Methods
Girolami, M. & Calderhead, B., J.R.Statist. Soc. B (2011), 73, 2, 1 - 37.
Advanced Monte Carlo methodology founded on geometric principles

6. Talk Outline
Motivation to improve MCMC capability for challenging problems

7. Talk Outline
Motivation to improve MCMC capability for challenging problems
Stochastic diffusion as adaptive proposal process

8. Talk Outline
Motivation to improve MCMC capability for challenging problems
Stochastic diffusion as adaptive proposal process
Exploring geometric concepts in MCMC methodology

9. Talk Outline
Motivation to improve MCMC capability for challenging problems
Stochastic diffusion as adaptive proposal process
Exploring geometric concepts in MCMC methodology
Diffusions across Riemann manifold as proposal mechanism

10. Talk Outline
Motivation to improve MCMC capability for challenging problems
Stochastic diffusion as adaptive proposal process
Exploring geometric concepts in MCMC methodology
Diffusions across Riemann manifold as proposal mechanism
Deterministic geodesic flows on manifold form basis of MCMC methods

11. Talk Outline
Motivation to improve MCMC capability for challenging problems
Stochastic diffusion as adaptive proposal process
Exploring geometric concepts in MCMC methodology
Diffusions across Riemann manifold as proposal mechanism
Deterministic geodesic flows on manifold form basis of MCMC methods
Illustrative Examples:-
Warped Bivariate Gaussian

12. Talk Outline
Motivation to improve MCMC capability for challenging problems
Stochastic diffusion as adaptive proposal process
Exploring geometric concepts in MCMC methodology
Diffusions across Riemann manifold as proposal mechanism
Deterministic geodesic flows on manifold form basis of MCMC methods
Illustrative Examples:-
Warped Bivariate Gaussian
Gaussian mixture model

13. Talk Outline
Motivation to improve MCMC capability for challenging problems
Stochastic diffusion as adaptive proposal process
Exploring geometric concepts in MCMC methodology
Diffusions across Riemann manifold as proposal mechanism
Deterministic geodesic flows on manifold form basis of MCMC methods
Illustrative Examples:-
Warped Bivariate Gaussian
Gaussian mixture model
Log-Gaussian Cox process

14. Talk Outline
Motivation to improve MCMC capability for challenging problems
Stochastic diffusion as adaptive proposal process
Exploring geometric concepts in MCMC methodology
Diffusions across Riemann manifold as proposal mechanism
Deterministic geodesic flows on manifold form basis of MCMC methods
Illustrative Examples:-
Warped Bivariate Gaussian
Gaussian mixture model
Log-Gaussian Cox process
Conclusions

15. Motivation Simulation Based Inference
Monte Carlo method employs samples from p(θ) to obtain estimate
Z
1 X 1
φ(θ)p(θ)dθ = φ(θ n ) + O(N − 2 )
N n

16. Motivation Simulation Based Inference
Monte Carlo method employs samples from p(θ) to obtain estimate
Z
1 X 1
φ(θ)p(θ)dθ = φ(θ n ) + O(N − 2 )
N n
Draw θ n from ergodic Markov process with stationary distribution p(θ)

17. Motivation Simulation Based Inference
Monte Carlo method employs samples from p(θ) to obtain estimate
Z
1 X 1
φ(θ)p(θ)dθ = φ(θ n ) + O(N − 2 )
N n
Draw θ n from ergodic Markov process with stationary distribution p(θ)
Construct process in two parts

18. Motivation Simulation Based Inference
Monte Carlo method employs samples from p(θ) to obtain estimate
Z
1 X 1
φ(θ)p(θ)dθ = φ(θ n ) + O(N − 2 )
N n
Draw θ n from ergodic Markov process with stationary distribution p(θ)
Construct process in two parts
Propose a move θ → θ with probability pp (θ |θ)

19. Motivation Simulation Based Inference
Monte Carlo method employs samples from p(θ) to obtain estimate
Z
1 X 1
φ(θ)p(θ)dθ = φ(θ n ) + O(N − 2 )
N n
Draw θ n from ergodic Markov process with stationary distribution p(θ)
Construct process in two parts
Propose a move θ → θ with probability pp (θ |θ)
accept or reject proposal with probability
» –
p(θ )pp (θ|θ )
pa (θ |θ) = min 1,
p(θ)pp (θ |θ)

20. Motivation Simulation Based Inference
Monte Carlo method employs samples from p(θ) to obtain estimate
Z
1 X 1
φ(θ)p(θ)dθ = φ(θ n ) + O(N − 2 )
N n
Draw θ n from ergodic Markov process with stationary distribution p(θ)
Construct process in two parts
Propose a move θ → θ with probability pp (θ |θ)
accept or reject proposal with probability
» –
p(θ )pp (θ|θ )
pa (θ |θ) = min 1,
p(θ)pp (θ |θ)
Efficiency dependent on pp (θ |θ) defining proposal mechanism

21. Motivation Simulation Based Inference
Monte Carlo method employs samples from p(θ) to obtain estimate
Z
1 X 1
φ(θ)p(θ)dθ = φ(θ n ) + O(N − 2 )
N n
Draw θ n from ergodic Markov process with stationary distribution p(θ)
Construct process in two parts
Propose a move θ → θ with probability pp (θ |θ)
accept or reject proposal with probability
» –
p(θ )pp (θ|θ )
pa (θ |θ) = min 1,
p(θ)pp (θ |θ)
Efficiency dependent on pp (θ |θ) defining proposal mechanism
Success of MCMC reliant upon appropriate proposal design

22. Adaptive Proposal Distributions - Exploit Discretised Diffusion

23. Adaptive Proposal Distributions - Exploit Discretised Diffusion
For θ ∈ RD with density p(θ), L(θ) ≡ log p(θ), define Langevin diffusion
1
dθ(t) = θ L(θ(t))dt + db(t)
2

24. Adaptive Proposal Distributions - Exploit Discretised Diffusion
For θ ∈ RD with density p(θ), L(θ) ≡ log p(θ), define Langevin diffusion
1
dθ(t) = θ L(θ(t))dt + db(t)
2
First order Euler-Maruyama discrete integration of diffusion
2
θ(τ + ) = θ(τ ) + θ L(θ(τ )) + z(τ )
2

25. Adaptive Proposal Distributions - Exploit Discretised Diffusion
For θ ∈ RD with density p(θ), L(θ) ≡ log p(θ), define Langevin diffusion
1
dθ(t) = θ L(θ(t))dt + db(t)
2
First order Euler-Maruyama discrete integration of diffusion
2
θ(τ + ) = θ(τ ) + θ L(θ(τ )) + z(τ )
2
Proposal 2
2
pp (θ |θ) = N (θ |µ(θ, ), I) with µ(θ, ) = θ + θ L(θ)
2

26. Adaptive Proposal Distributions - Exploit Discretised Diffusion
For θ ∈ RD with density p(θ), L(θ) ≡ log p(θ), define Langevin diffusion
1
dθ(t) = θ L(θ(t))dt + db(t)
2
First order Euler-Maruyama discrete integration of diffusion
2
θ(τ + ) = θ(τ ) + θ L(θ(τ )) + z(τ )
2
Proposal 2
2
pp (θ |θ) = N (θ |µ(θ, ), I) with µ(θ, ) = θ + θ L(θ)
2
Acceptance probability to correct for bias
» –
p(θ )pp (θ|θ )
pa (θ |θ) = min 1,
p(θ)pp (θ |θ)

27. Adaptive Proposal Distributions - Exploit Discretised Diffusion
For θ ∈ RD with density p(θ), L(θ) ≡ log p(θ), define Langevin diffusion
1
dθ(t) = θ L(θ(t))dt + db(t)
2
First order Euler-Maruyama discrete integration of diffusion
2
θ(τ + ) = θ(τ ) + θ L(θ(τ )) + z(τ )
2
Proposal 2
2
pp (θ |θ) = N (θ |µ(θ, ), I) with µ(θ, ) = θ + θ L(θ)
2
Acceptance probability to correct for bias
» –
p(θ )pp (θ|θ )
pa (θ |θ) = min 1,
p(θ)pp (θ |θ)
Isotropic diffusion inefficient, employ pre-conditioning
√
θ = θ + 2 M θ L(θ)/2 + Mz

28. Adaptive Proposal Distributions - Exploit Discretised Diffusion
For θ ∈ RD with density p(θ), L(θ) ≡ log p(θ), define Langevin diffusion
1
dθ(t) = θ L(θ(t))dt + db(t)
2
First order Euler-Maruyama discrete integration of diffusion
2
θ(τ + ) = θ(τ ) + θ L(θ(τ )) + z(τ )
2
Proposal 2
2
pp (θ |θ) = N (θ |µ(θ, ), I) with µ(θ, ) = θ + θ L(θ)
2
Acceptance probability to correct for bias
» –
p(θ )pp (θ|θ )
pa (θ |θ) = min 1,
p(θ)pp (θ |θ)
Isotropic diffusion inefficient, employ pre-conditioning
√
θ = θ + 2 M θ L(θ)/2 + Mz
How to set M systematically? Tuning in transient & stationary phases

29. Geometric Concepts in MCMC

30. Geometric Concepts in MCMC
Rao, 1945; Jeffreys, 1948, to first order
Z
p(y; θ + δθ)
p(y; θ + δθ) log dθ ≈ δθ T G(θ)δθ
p(y; θ)

31. Geometric Concepts in MCMC
Rao, 1945; Jeffreys, 1948, to first order
Z
p(y; θ + δθ)
p(y; θ + δθ) log dθ ≈ δθ T G(θ)δθ
p(y; θ)
where ( )
T
θ p(y; θ) θ p(y; θ)
G(θ) = Ey|θ
p(y; θ) p(y; θ)

32. Geometric Concepts in MCMC
Rao, 1945; Jeffreys, 1948, to first order
Z
p(y; θ + δθ)
p(y; θ + δθ) log dθ ≈ δθ T G(θ)δθ
p(y; θ)
where ( )
T
θ p(y; θ) θ p(y; θ)
G(θ) = Ey|θ
p(y; θ) p(y; θ)
Fisher Information G(θ) is p.d. metric defining a Riemann manifold

33. Geometric Concepts in MCMC
Rao, 1945; Jeffreys, 1948, to first order
Z
p(y; θ + δθ)
p(y; θ + δθ) log dθ ≈ δθ T G(θ)δθ
p(y; θ)
where ( )
T
θ p(y; θ) θ p(y; θ)
G(θ) = Ey|θ
p(y; θ) p(y; θ)
Fisher Information G(θ) is p.d. metric defining a Riemann manifold
Non-Euclidean geometry for probabilities - distances, metrics, invariants,
curvature, geodesics

34. Geometric Concepts in MCMC
Rao, 1945; Jeffreys, 1948, to first order
Z
p(y; θ + δθ)
p(y; θ + δθ) log dθ ≈ δθ T G(θ)δθ
p(y; θ)
where ( )
T
θ p(y; θ) θ p(y; θ)
G(θ) = Ey|θ
p(y; θ) p(y; θ)
Fisher Information G(θ) is p.d. metric defining a Riemann manifold
Non-Euclidean geometry for probabilities - distances, metrics, invariants,
curvature, geodesics
Asymptotic statistical analysis. Amari, 1981, 85, 90; Murray & Rice,
1993; Critchley et al, 1993; Kass, 1989; Efron, 1975; Dawid, 1975;
Lauritsen, 1989

35. Geometric Concepts in MCMC
Rao, 1945; Jeffreys, 1948, to first order
Z
p(y; θ + δθ)
p(y; θ + δθ) log dθ ≈ δθ T G(θ)δθ
p(y; θ)
where ( )
T
θ p(y; θ) θ p(y; θ)
G(θ) = Ey|θ
p(y; θ) p(y; θ)
Fisher Information G(θ) is p.d. metric defining a Riemann manifold
Non-Euclidean geometry for probabilities - distances, metrics, invariants,
curvature, geodesics
Asymptotic statistical analysis. Amari, 1981, 85, 90; Murray & Rice,
1993; Critchley et al, 1993; Kass, 1989; Efron, 1975; Dawid, 1975;
Lauritsen, 1989
Statistical shape analysis Kent et al, 1996; Dryden & Mardia, 1998

36. Geometric Concepts in MCMC
Rao, 1945; Jeffreys, 1948, to first order
Z
p(y; θ + δθ)
p(y; θ + δθ) log dθ ≈ δθ T G(θ)δθ
p(y; θ)
where ( )
T
θ p(y; θ) θ p(y; θ)
G(θ) = Ey|θ
p(y; θ) p(y; θ)
Fisher Information G(θ) is p.d. metric defining a Riemann manifold
Non-Euclidean geometry for probabilities - distances, metrics, invariants,
curvature, geodesics
Asymptotic statistical analysis. Amari, 1981, 85, 90; Murray & Rice,
1993; Critchley et al, 1993; Kass, 1989; Efron, 1975; Dawid, 1975;
Lauritsen, 1989
Statistical shape analysis Kent et al, 1996; Dryden & Mardia, 1998
Can geometric structure be employed in MCMC methodology?

37. Geometric Concepts in MCMC

38. Geometric Concepts in MCMC
Tangent space - local metric defined by δθ T G(θ)δθ =
P
k ,l gkl δθk δθl

39. Geometric Concepts in MCMC
Tangent space - local metric defined by δθ T G(θ)δθ = k ,l gkl δθk δθl
P
Christoffel symbols - characterise connection on curved manifold

40. Geometric Concepts in MCMC
Tangent space - local metric defined by δθ T G(θ)δθ = k ,l gkl δθk δθl
P
Christoffel symbols - characterise connection on curved manifold
„ «
1 X im ∂gmk ∂gml ∂gkl
Γikl = g + − m
2 m ∂θl ∂θk ∂θ

41. Geometric Concepts in MCMC
Tangent space - local metric defined by δθ T G(θ)δθ = k ,l gkl δθk δθl
P
Christoffel symbols - characterise connection on curved manifold
„ «
1 X im ∂gmk ∂gml ∂gkl
Γikl = g + − m
2 m ∂θl ∂θk ∂θ
Geodesics - shortest path between two points on manifold

42. Geometric Concepts in MCMC
Tangent space - local metric defined by δθ T G(θ)δθ = k ,l gkl δθk δθl
P
Christoffel symbols - characterise connection on curved manifold
„ «
1 X im ∂gmk ∂gml ∂gkl
Γikl = g + − m
2 m ∂θl ∂θk ∂θ
Geodesics - shortest path between two points on manifold
d 2 θi X i dθk dθl
+ Γkl =0
dt 2 dt dt
k,l

43. Illustration of Geometric Concepts
Consider Normal density p(x|µ, σ) = Nx (µ, σ)

44. Illustration of Geometric Concepts
Consider Normal density p(x|µ, σ) = Nx (µ, σ)
Local inner product on tangent space defined by metric tensor, i.e.
δθ T G(θ)δθ, where θ = (µ, σ)T

45. Illustration of Geometric Concepts
Consider Normal density p(x|µ, σ) = Nx (µ, σ)
Local inner product on tangent space defined by metric tensor, i.e.
δθ T G(θ)δθ, where θ = (µ, σ)T
Metric is Fisher Information
σ −2
» –
0
G(µ, σ) =
0 2σ −2

46. Illustration of Geometric Concepts
Consider Normal density p(x|µ, σ) = Nx (µ, σ)
Local inner product on tangent space defined by metric tensor, i.e.
δθ T G(θ)δθ, where θ = (µ, σ)T
Metric is Fisher Information
σ −2
» –
0
G(µ, σ) =
0 2σ −2
Inner-product σ −2 (δµ2 + 2δσ 2 ) so densities N (0, 1) & N (1, 1) further
apart than the densities N (0, 2) & N (1, 2) - distance non-Euclidean

47. Illustration of Geometric Concepts
Consider Normal density p(x|µ, σ) = Nx (µ, σ)
Local inner product on tangent space defined by metric tensor, i.e.
δθ T G(θ)δθ, where θ = (µ, σ)T
Metric is Fisher Information
σ −2
» –
0
G(µ, σ) =
0 2σ −2
Inner-product σ −2 (δµ2 + 2δσ 2 ) so densities N (0, 1) & N (1, 1) further
apart than the densities N (0, 2) & N (1, 2) - distance non-Euclidean
Metric tensor for univariate Normal defines a Hyperbolic Space

48. M.C. Escher, Heaven and Hell, 1960

49. Langevin Diffusion on Riemannian manifold
Discretised Langevin diffusion on manifold defines proposal mechanism
2 “ ” D
X “p ”
θd = θd + G −1 (θ) θ L(θ) − 2
G(θ)−1 Γd +
ij ij G−1 (θ)z
2 d d
i,j

50. Langevin Diffusion on Riemannian manifold
Discretised Langevin diffusion on manifold defines proposal mechanism
2 “ ” D
X “p ”
θd = θd + G −1 (θ) θ L(θ) − 2
G(θ)−1 Γd +
ij ij G−1 (θ)z
2 d d
i,j
Manifold with constant curvature then proposal mechanism reduces to
2
G −1 (θ)
p
θ =θ+ θ L(θ) + G−1 (θ)z
2

51. Langevin Diffusion on Riemannian manifold
Discretised Langevin diffusion on manifold defines proposal mechanism
2 “ ” D
X “p ”
θd = θd + G −1 (θ) θ L(θ) − 2
G(θ)−1 Γd +
ij ij G−1 (θ)z
2 d d
i,j
Manifold with constant curvature then proposal mechanism reduces to
2
G −1 (θ) θ L(θ) +
p
θ =θ+ G−1 (θ)z
2
MALA proposal with preconditioning
2 √
θ =θ+ M θ L(θ) + Mz
2

52. Langevin Diffusion on Riemannian manifold
Discretised Langevin diffusion on manifold defines proposal mechanism
2 “ ” D
X “p ”
θd = θd + G −1 (θ) θ L(θ) − 2
G(θ)−1 Γd +
ij ij G−1 (θ)z
2 d d
i,j
Manifold with constant curvature then proposal mechanism reduces to
2
G −1 (θ) θ L(θ) +
p
θ =θ+ G−1 (θ)z
2
MALA proposal with preconditioning
2 √
θ =θ+ M θ L(θ) + Mz
2
Proposal and acceptance probability
pp (θ |θ) = N (θ |µ(θ, ), 2 G(θ))
» –
p(θ )pp (θ|θ )
pa (θ |θ) = min 1,
p(θ)pp (θ |θ)

53. Langevin Diffusion on Riemannian manifold
Discretised Langevin diffusion on manifold defines proposal mechanism
2 “ ” D
X “p ”
θd = θd + G −1 (θ) θ L(θ) − 2
G(θ)−1 Γd +
ij ij G−1 (θ)z
2 d d
i,j
Manifold with constant curvature then proposal mechanism reduces to
2
G −1 (θ) θ L(θ) +
p
θ =θ+ G−1 (θ)z
2
MALA proposal with preconditioning
2 √
θ =θ+ M θ L(θ) + Mz
2
Proposal and acceptance probability
pp (θ |θ) = N (θ |µ(θ, ), 2 G(θ))
» –
p(θ )pp (θ|θ )
pa (θ |θ) = min 1,
p(θ)pp (θ |θ)
Proposal mechanism diffuses approximately along the manifold

54. Langevin Diffusion on Riemannian manifold
40 40
35 35
30 30
25 25
!
!
20 20
15 15
10 10
5 5
−5 0 5 −5 0 5
µ µ

55. Langevin Diffusion on Riemannian manifold
25 25
20 20
15 15
!
!
10 10
5 5
−10 0 10 −10 0 10
µ µ

56. Geodesic flow as proposal mechanism
Desirable that proposals follow direct path on manifold - geodesics

57. Geodesic flow as proposal mechanism
Desirable that proposals follow direct path on manifold - geodesics
Define geodesic flow on manifold by solving
d 2 θi X i dθk dθl
+ Γkl =0
dt 2 dt dt
k,l

58. Geodesic flow as proposal mechanism
Desirable that proposals follow direct path on manifold - geodesics
Define geodesic flow on manifold by solving
d 2 θi X i dθk dθl
+ Γkl =0
dt 2 dt dt
k,l
How can this be exploited in the design of a transition operator?

59. Geodesic flow as proposal mechanism
Desirable that proposals follow direct path on manifold - geodesics
Define geodesic flow on manifold by solving
d 2 θi X i dθk dθl
+ Γkl =0
dt 2 dt dt
k,l
How can this be exploited in the design of a transition operator?
Need slight detour

60. Geodesic flow as proposal mechanism
Desirable that proposals follow direct path on manifold - geodesics
Define geodesic flow on manifold by solving
d 2 θi X i dθk dθl
+ Γkl =0
dt 2 dt dt
k,l
How can this be exploited in the design of a transition operator?
Need slight detour - first define log-density under model as L(θ)

61. Geodesic flow as proposal mechanism
Desirable that proposals follow direct path on manifold - geodesics
Define geodesic flow on manifold by solving
d 2 θi X i dθk dθl
+ Γkl =0
dt 2 dt dt
k,l
How can this be exploited in the design of a transition operator?
Need slight detour - first define log-density under model as L(θ)
Introduce auxiliary variable p ∼ N (0, G(θ))

62. Geodesic flow as proposal mechanism
Desirable that proposals follow direct path on manifold - geodesics
Define geodesic flow on manifold by solving
d 2 θi X i dθk dθl
+ Γkl =0
dt 2 dt dt
k,l
How can this be exploited in the design of a transition operator?
Need slight detour - first define log-density under model as L(θ)
Introduce auxiliary variable p ∼ N (0, G(θ))
Negative joint log density is
1 1
H(θ, p) = −L(θ) + log 2π D |G(θ)| + pT G(θ)−1 p
2 2

63. Riemannian Hamiltonian Monte Carlo
Negative joint log-density ≡ Hamiltonian defined on Riemann manifold
1 1
H(θ, p) = −L(θ) + log 2π D |G(θ)| + pT G(θ)−1 p
| 2 {z } |2 {z }
Potential Energy Kinetic Energy

64. Riemannian Hamiltonian Monte Carlo
Negative joint log-density ≡ Hamiltonian defined on Riemann manifold
1 1
H(θ, p) = −L(θ) + log 2π D |G(θ)| + pT G(θ)−1 p
| 2 {z } |2 {z }
Potential Energy Kinetic Energy
Marginal density follows as required
Z  ff
exp {L(θ)} 1
p(θ) ∝ p exp − pT G(θ)−1 p dp = exp {L(θ)}
2π D |G(θ)| 2

65. Riemannian Hamiltonian Monte Carlo
Negative joint log-density ≡ Hamiltonian defined on Riemann manifold
1 1
H(θ, p) = −L(θ) + log 2π D |G(θ)| + pT G(θ)−1 p
| 2 {z } |2 {z }
Potential Energy Kinetic Energy
Marginal density follows as required
Z  ff
exp {L(θ)} 1
p(θ) ∝ p exp − pT G(θ)−1 p dp = exp {L(θ)}
2π D |G(θ)| 2
Obtain samples from marginal p(θ) using Gibbs sampler for p(θ, p)
pn+1 |θ n ∼ N (0, G(θ n ))
n+1 n+1
θ |p ∼ p(θ n+1 |pn+1 )

66. Riemannian Hamiltonian Monte Carlo
Negative joint log-density ≡ Hamiltonian defined on Riemann manifold
1 1
H(θ, p) = −L(θ) + log 2π D |G(θ)| + pT G(θ)−1 p
| 2 {z } |2 {z }
Potential Energy Kinetic Energy
Marginal density follows as required
Z  ff
exp {L(θ)} 1
p(θ) ∝ p exp − pT G(θ)−1 p dp = exp {L(θ)}
2π D |G(θ)| 2
Obtain samples from marginal p(θ) using Gibbs sampler for p(θ, p)
pn+1 |θ n ∼ N (0, G(θ n ))
n+1 n+1
θ |p ∼ p(θ n+1 |pn+1 )
Employ Hamiltonian dynamics to propose samples for p(θ n+1 |pn+1 ),
Duane et al, 1987; Neal, 2010.

67. Riemannian Hamiltonian Monte Carlo
Negative joint log-density ≡ Hamiltonian defined on Riemann manifold
1 1
H(θ, p) = −L(θ) + log 2π D |G(θ)| + pT G(θ)−1 p
| 2 {z } |2 {z }
Potential Energy Kinetic Energy
Marginal density follows as required
Z  ff
exp {L(θ)} 1
p(θ) ∝ p exp − pT G(θ)−1 p dp = exp {L(θ)}
2π D |G(θ)| 2
Obtain samples from marginal p(θ) using Gibbs sampler for p(θ, p)
pn+1 |θ n ∼ N (0, G(θ n ))
n+1 n+1
θ |p ∼ p(θ n+1 |pn+1 )
Employ Hamiltonian dynamics to propose samples for p(θ n+1 |pn+1 ),
Duane et al, 1987; Neal, 2010.
dθ ∂ dp ∂
= H(θ, p) = − H(θ, p)
dt ∂p dt ∂θ

68. Riemannian Manifold Hamiltonian Monte Carlo
˜ ˜
Consider the Hamiltonian H(θ, p) = 1 pT G(θ)−1 p
2

69. Riemannian Manifold Hamiltonian Monte Carlo
˜ ˜
Consider the Hamiltonian H(θ, p) = 1 pT G(θ)−1 p
2
Hamiltonians with only a quadratic kinetic energy term exactly describe
geodesic flow on the coordinate space θ with metric G ˜

70. Riemannian Manifold Hamiltonian Monte Carlo
˜ ˜
Consider the Hamiltonian H(θ, p) = 1 pT G(θ)−1 p
2
Hamiltonians with only a quadratic kinetic energy term exactly describe
geodesic flow on the coordinate space θ with metric G ˜
However our Hamiltonian is H(θ, p) = V (θ) + 1 pT G(θ)−1 p
2

71. Riemannian Manifold Hamiltonian Monte Carlo
˜ ˜
Consider the Hamiltonian H(θ, p) = 1 pT G(θ)−1 p
2
Hamiltonians with only a quadratic kinetic energy term exactly describe
geodesic flow on the coordinate space θ with metric G ˜
However our Hamiltonian is H(θ, p) = V (θ) + 1 pT G(θ)−1 p
2
˜
If we define G(θ) = G(θ) × (h − V (θ)), where h is a constant H(θ, p)

72. Riemannian Manifold Hamiltonian Monte Carlo
˜ ˜
Consider the Hamiltonian H(θ, p) = 1 pT G(θ)−1 p
2
Hamiltonians with only a quadratic kinetic energy term exactly describe
geodesic flow on the coordinate space θ with metric G ˜
However our Hamiltonian is H(θ, p) = V (θ) + 1 pT G(θ)−1 p
2
˜
If we define G(θ) = G(θ) × (h − V (θ)), where h is a constant H(θ, p)
Then the Maupertuis principle tells us that the Hamiltonian flow for
˜
H(θ, p) and H(θ, p) are equivalent along energy level h

73. Riemannian Manifold Hamiltonian Monte Carlo
˜ ˜
Consider the Hamiltonian H(θ, p) = 1 pT G(θ)−1 p
2
Hamiltonians with only a quadratic kinetic energy term exactly describe
geodesic flow on the coordinate space θ with metric G ˜
However our Hamiltonian is H(θ, p) = V (θ) + 1 pT G(θ)−1 p
2
˜
If we define G(θ) = G(θ) × (h − V (θ)), where h is a constant H(θ, p)
Then the Maupertuis principle tells us that the Hamiltonian flow for
˜
H(θ, p) and H(θ, p) are equivalent along energy level h
The solution of
dθ ∂ dp ∂
= H(θ, p) = − H(θ, p)
dt ∂p dt ∂θ

74. Riemannian Manifold Hamiltonian Monte Carlo
˜ ˜
Consider the Hamiltonian H(θ, p) = 1 pT G(θ)−1 p
2
Hamiltonians with only a quadratic kinetic energy term exactly describe
geodesic flow on the coordinate space θ with metric G ˜
However our Hamiltonian is H(θ, p) = V (θ) + 1 pT G(θ)−1 p
2
˜
If we define G(θ) = G(θ) × (h − V (θ)), where h is a constant H(θ, p)
Then the Maupertuis principle tells us that the Hamiltonian flow for
˜
H(θ, p) and H(θ, p) are equivalent along energy level h
The solution of
dθ ∂ dp ∂
= H(θ, p) = − H(θ, p)
dt ∂p dt ∂θ
is therefore equivalent to the solution of
d 2 θi X i dθk dθl
˜
+ Γkl =0
dt 2 dt dt
k,l

75. Riemannian Manifold Hamiltonian Monte Carlo
˜ ˜
Consider the Hamiltonian H(θ, p) = 1 pT G(θ)−1 p
2
Hamiltonians with only a quadratic kinetic energy term exactly describe
geodesic flow on the coordinate space θ with metric G ˜
However our Hamiltonian is H(θ, p) = V (θ) + 1 pT G(θ)−1 p
2
˜
If we define G(θ) = G(θ) × (h − V (θ)), where h is a constant H(θ, p)
Then the Maupertuis principle tells us that the Hamiltonian flow for
˜
H(θ, p) and H(θ, p) are equivalent along energy level h
The solution of
dθ ∂ dp ∂
= H(θ, p) = − H(θ, p)
dt ∂p dt ∂θ
is therefore equivalent to the solution of
d 2 θi X i dθk dθl
˜
+ Γkl =0
dt 2 dt dt
k,l
RMHMC proposals are along the manifold geodesics

76. Warped Bivariate Gaussian
QN 2 2 2
p(w1 , w2 |y, σx , σy ) ∝ n=1 N (yn |w1 + w2 , σy )N (w1 , w2 |0, σx I)

77. Warped Bivariate Gaussian
QN 2 2 2
p(w1 , w2 |y, σx , σy ) ∝ n=1 N (yn |w1 + w2 , σy )N (w1 , w2 |0, σx I)
3 3
HMC RMHMC
2 2
1 1
w 0 w 0
-1 -1
-2 -2
-3 -3
-4 -3 -2 -1 0 1 2 3 -4 -3 -2 -1 0 1 2 3
w w

78. Gaussian Mixture Model
Univariate finite mixture model
K
X 2
p(xi |θ) = πk N (xi |µk , σk )
k=1

79. Gaussian Mixture Model
Univariate finite mixture model
K
X 2
p(xi |θ) = πk N (xi |µk , σk )
k=1
FI based metric tensor non-analytic - employ empirical FI

80. Gaussian Mixture Model
Univariate finite mixture model
K
X 2
p(xi |θ) = πk N (xi |µk , σk )
k=1
FI based metric tensor non-analytic - employ empirical FI
1 T 1
G(θ) = S S − 2 ssT
¯¯ −−→
−− cov ( θ L(θ)) = I(θ)
N N N→∞
!
∂S T ∂ sT
„ «
∂G(θ) 1 ∂S 1 ¯
∂s T ¯
= S + ST − ¯ ¯
s +s
∂θd N ∂θd ∂θd N2 ∂θd ∂θd
∂ log p(xi |θ) PN
with score matrix S with elements Si,d = ∂θd
¯
and s = i=1 ST
i,·

81. Gaussian Mixture Model
Univariate finite mixture model
p(x|µ, σ 2 ) = 0.7 × N (x|0, σ 2 ) + 0.3 × N (x|µ, σ 2 )

82. Gaussian Mixture Model
Univariate finite mixture model
p(x|µ, σ 2 ) = 0.7 × N (x|0, σ 2 ) + 0.3 × N (x|µ, σ 2 )
4
3
2
1
lnσ
0
−1
−2
−3
−4
−4 −3 −2 −1 0 1 2 3 4
µ
Figure: Arrows correspond to the gradients and ellipses to the inverse metric
tensor. Dashed lines are isocontours of the joint log density

83. Gaussian Mixture Model
MALA path mMALA path Simplified mMALA path
4 4 4
−1410 −1410 −1410
−1310 −1310 −1310
3 3 3
−1210 −1210 −1210
−1110 −1110 −1110
2 2 2
−1010 −1010 −1010
1 1 1
−910 −910 −910
lnσ
lnσ
lnσ
0 0 0
−1 −1 −1
−1410 −1410 −1410
−2 −2 −2
−2910 −2910 −2910
−3 −3 −3
−4 −4 −4
−4 −3 −2 −1 0 1 2 3 4 −4 −3 −2 −1 0 1 2 3 4 −4 −3 −2 −1 0 1 2 3 4
µ µ µ
MALA Sample Autocorrelation Function mMALA Sample Autocorrelation Function Simplified mMALA Sample Autocorrelation Function
0.8 0.8 0.8
Sample Autocorrelation
Sample Autocorrelation
Sample Autocorrelation
0.6 0.6 0.6
0.4 0.4 0.4
0.2 0.2 0.2
0 0 0
−0.2 −0.2 −0.2
0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16 18 20
Lag Lag Lag
Figure: Comparison of MALA (left), mMALA (middle) and simplified mMALA (right)
convergence paths and autocorrelation plots. Autocorrelation plots are from the
stationary chains, i.e. once the chains have converged to the stationary distribution.

84. Gaussian Mixture Model
HMC path RMHMC path Gibbs path
4 4 4
−1410 −1410 −1410
−1310 −1310 −1310
3 3 3
−1210 −1210 −1210
−1110 −1110 −1110
2 2 2
−1010 −1010 −1010
1 1 1
−910 −910 −910
lnσ
lnσ
lnσ
0 0 0
−1 −1 −1
−1410 −1410 −1410
−2 −2 −2
−2910 −2910 −2910
−3 −3 −3
−4 −4 −4
−4 −3 −2 −1 0 1 2 3 4 −4 −3 −2 −1 0 1 2 3 4 −4 −3 −2 −1 0 1 2 3 4
µ µ µ
HMC Sample Autocorrelation Function RMHMC Sample Autocorrelation Function Gibbs Sample Autocorrelation Function
0.8 0.8 0.8
Sample Autocorrelation
Sample Autocorrelation
Sample Autocorrelation
0.6 0.6 0.6
0.4 0.4 0.4
0.2 0.2 0.2
0 0 0
−0.2 −0.2 −0.2
0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16 18 20
Lag Lag Lag
Figure: Comparison of HMC (left), RMHMC (middle) and GIBBS (right) convergence
paths and autocorrelation plots. Autocorrelation plots are from the stationary chains,
i.e. once the chains have converged to the stationary distribution.

85. Log-Gaussian Cox Point Process with Latent Field
The joint density for Poisson counts and latent Gaussian field
Y64
p(y, x|µ, σ, β) ∝ exp{yi,j xi,j −m exp(xi,j )} exp(−(x−µ1)T Σ−1 (x−µ1)/2)
θ
i,j

86. Log-Gaussian Cox Point Process with Latent Field
The joint density for Poisson counts and latent Gaussian field
Y64
p(y, x|µ, σ, β) ∝ exp{yi,j xi,j −m exp(xi,j )} exp(−(x−µ1)T Σ−1 (x−µ1)/2)
θ
i,j
Metric tensors
„ «
1 ∂Σθ −1 ∂Σθ
G(θ)i,j = trace Σ−1
θ Σθ
2 ∂θi ∂θj
G(x) = Λ + Σ−1
θ
where Λ is diagonal with elements m exp(µ + (Σθ )i,i )

87. Log-Gaussian Cox Point Process with Latent Field
The joint density for Poisson counts and latent Gaussian field
Y64
p(y, x|µ, σ, β) ∝ exp{yi,j xi,j −m exp(xi,j )} exp(−(x−µ1)T Σ−1 (x−µ1)/2)
θ
i,j
Metric tensors
„ «
1 ∂Σθ −1 ∂Σθ
G(θ)i,j = trace Σ−1
θ Σθ
2 ∂θi ∂θj
G(x) = Λ + Σ−1
θ
where Λ is diagonal with elements m exp(µ + (Σθ )i,i )
Latent field metric tensor defining flat manifold is 4096 × 4096, O(N 3 )
obtained from parameter conditional

88. Log-Gaussian Cox Point Process with Latent Field
The joint density for Poisson counts and latent Gaussian field
Y64
p(y, x|µ, σ, β) ∝ exp{yi,j xi,j −m exp(xi,j )} exp(−(x−µ1)T Σ−1 (x−µ1)/2)
θ
i,j
Metric tensors
„ «
1 ∂Σθ −1 ∂Σθ
G(θ)i,j = trace Σ−1
θ Σθ
2 ∂θi ∂θj
G(x) = Λ + Σ−1
θ
where Λ is diagonal with elements m exp(µ + (Σθ )i,i )
Latent field metric tensor defining flat manifold is 4096 × 4096, O(N 3 )
obtained from parameter conditional
MALA requires transformation of latent field to sample - with separate
tuning in transient and stationary phases of Markov chain
Manifold methods requires no pilot tuning or additional transformations

89. RMHMC for Log-Gaussian Cox Point Processes
Table: Sampling the latent variables of a Log-Gaussian Cox Process - Comparison of
sampling methods
Method Time ESS (Min, Med, Max) s/Min ESS Rel. Speed
MALA (Transient) 31,577 (3, 8, 50) 10,605 ×1
MALA (Stationary) 31,118 (4, 16, 80) 7836 ×1.35
mMALA 634 (26, 84, 174) 24.1 ×440
RMHMC 2936 (1951, 4545, 5000) 1.5 ×7070

90. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods

91. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA

92. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC

93. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models

94. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology

95. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology
Ongoing development

96. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology
Ongoing development
Potential bottleneck at metric tensor and Christoffel symbols

97. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology
Ongoing development
Potential bottleneck at metric tensor and Christoffel symbols
Theoretical analysis of convergence

98. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology
Ongoing development
Potential bottleneck at metric tensor and Christoffel symbols
Theoretical analysis of convergence
Investigate alternative manifold structures

99. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology
Ongoing development
Potential bottleneck at metric tensor and Christoffel symbols
Theoretical analysis of convergence
Investigate alternative manifold structures
Design and effect of metric

100. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology
Ongoing development
Potential bottleneck at metric tensor and Christoffel symbols
Theoretical analysis of convergence
Investigate alternative manifold structures
Design and effect of metric
Optimality of Hamiltonian flows as local geodesics

101. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology
Ongoing development
Potential bottleneck at metric tensor and Christoffel symbols
Theoretical analysis of convergence
Investigate alternative manifold structures
Design and effect of metric
Optimality of Hamiltonian flows as local geodesics
Alternative transition kernels

102. Conclusion and Discussion
Geometry of statistical models harnessed in Monte Carlo methods
Diffusions that respect structure and curvature of space - Manifold MALA
Geodesic flows on model manifold - RMHMC - generalisation of HMC
Assessed on correlated & high-dimensional latent variable models
Promising capability of methodology
Ongoing development
Potential bottleneck at metric tensor and Christoffel symbols
Theoretical analysis of convergence
Investigate alternative manifold structures
Design and effect of metric
Optimality of Hamiltonian flows as local geodesics
Alternative transition kernels
No silver bullet or cure all - new powerful methodology for MC toolkit

103. Funding Acknowledgment
Girolami funded by EPSRC Advanced Research Fellowship and BBSRC
project grant
Calderhead supported by Microsoft Research PhD Scholarship