The document discusses advancements in robotics and deep learning, particularly highlighting the transition from traditional feature extraction methods to deep supervised learning for object detection and reinforcement learning for robotic control. It covers significant models like the Deep Q-Network (DQN) and various optimization strategies including policy gradients, with practical applications in locomotion tasks. Additionally, it addresses challenges in training robots for complex dynamics and visuo-motor skills, while exploring future frontiers in robotics and AI.

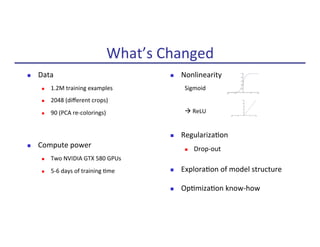
![n State-of-the-art object detec9on un9l 2012:
n Deep Supervised Learning (Krizhevsky, Sutskever, Hinton 2012; also LeCun, Bengio, Ng, Darrell, …):
n ~1.2 million training images from ImageNet [Deng, Dong, Socher, Li, Li, Fei-Fei, 2009]
Object Detec9on in Computer Vision
Input
Image
Hand-engineered
features (SIFT,
HOG, DAISY, …)
Support
Vector
Machine
(SVM)
“cat”
“dog”
“car”
…
Input
Image
8-layer neural network with 60 million
parameters to learn
“cat”
“dog”
“car”
…](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-2-320.jpg)


![n State-of-the-art object detec9on un9l 2012:
n Deep Supervised Learning (Krizhevsky, Sutskever, Hinton 2012; also LeCun, Bengio, Ng, Darrell, …):
n ~1.2 million training images from ImageNet [Deng, Dong, Socher, Li, Li, Fei-Fei, 2009]
Object Detec9on in Computer Vision
Input
Image
Hand-engineered
features (SIFT,
HOG, DAISY, …)
Support
Vector
Machine
(SVM)
“cat”
“dog”
“car”
…
Input
Image
8-layer neural network with 60 million
parameters to learn
“cat”
“dog”
“car”
…](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-11-320.jpg)
![Reinforcement Learning
n Goal:
max
✓
E[
HX
t=0
R(st)|⇡✓]
probability of taking ac9on a in state s
Robot +
Environment
⇡✓(a|s)](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-13-320.jpg)

![[Source: Mnih et al., Nature 2015 (DeepMind) ]
Deep Q-Network (DQN): From Pixels to Joys9ck Commands
32 8x8 filters with stride 4 + ReLU
64 4x4 filters with stride 2 + ReLU
64 3x3 filters with stride 1 + ReLU
fully connected 512 units + ReLU
fully connected output units, one per ac9on](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-15-320.jpg)
![[ Source: Mnih et al., Nature 2015 (DeepMind) ]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-16-320.jpg)

![How About Con9nuous Control, e.g., Locomo9on?
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
[18] Michail G Lagoudakis and Ronald Parr. Reinforcement learning as classification: Leveraging modern
classifiers. In ICML, volume 3, pages 424–431, 2003.
[19] Dimitri P Bertsekas. Dynamic programming and optimal control, volume 1. Athena Scientific Belmont,
MA, 3rd edition, 2005.
[20] Andrew Y Ng and Michael Jordan. Pegasus: A policy search method for large mdps and pomdps. In
Proceedings of the Sixteenth conference on Uncertainty in artificial intelligence, pages 406–415. Morgan
Kaufmann Publishers Inc., 2000.
[21] Jan Peters and Stefan Schaal. Natural actor-critic. Neurocomputing, 71(7):1180–1190, 2008.
[22] Emanuel Todorov, Tom Erez, and Yuval Tassa. Mujoco: A physics engine for model-based control. In
Intelligent Robots and Systems (IROS), 2012 IEEE/RSJ International Conference on, pages 5026–5033.
IEEE, 2012.
[23] Jan Peters and Stefan Schaal. Reinforcement learning by reward-weighted regression for operational
space control. In Proceedings of the 24th international conference on Machine learning, pages 745–750.
ACM, 2007.
[24] Andrew G Barto, Richard S Sutton, and Charles W Anderson. Neuronlike adaptive elements that can solve
difficult learning control problems. Systems, Man and Cybernetics, IEEE Transactions on, (5):834–846,
1983.
[25] David Asher Levin, Yuval Peres, and Elizabeth Lee Wilmer. Markov chains and mixing times. American
Mathematical Society, 2009.
[26] Stephen J Wright and Jorge Nocedal. Numerical optimization, volume 2. Springer New York, 1999.
[27] Razvan Pascanu and Yoshua Bengio. Revisiting natural gradient for deep networks. arXiv preprint
arXiv:1301.3584, 2013.
[28] James Bergstra et al. Theano: a CPU and GPU math expression compiler.
A Approximating policies with neural networks
Jointanglesandkinematics
Control
Standard
deviations
Fully
connected
layer
30 units
Input
layer
Mean
parameters
Sampling
Figure 4: Neural network architecture for the locomotion domain: Two fully connected hidden lay-
ers transform the input to the mean µ of a Normal distribution from which the controls are sampled.
To represent the stochastic policy ⇡✓, we use a neural network with weights ✓. The network maps the
observations to a set of parameters indexing the probability distribution that is then used to sample
the controls for the rollouts. We now describe the architecture used in the respective domains in
more detail.
13
Neural network architecture:
Input: joint angles and veloci9es
Output: joint torques
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
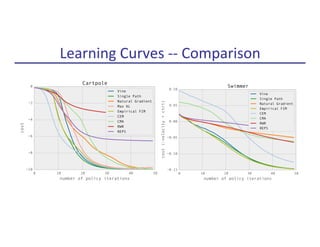
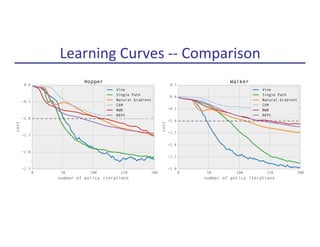
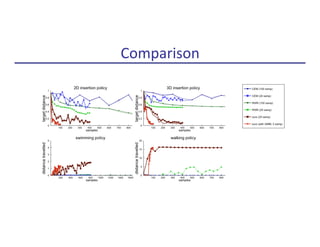
Figure 1: Robot models used for locomotion experiments, instantiated in MuJoCo physics simulator.
The three models on the left are constrained to two dimensions and are called the swimmer, hopper,
and walker—these models were used for the main experimental comparisons.
two other approaches: reward-weighted regression (RWR) [23]4
and the cross entropy method. All
of the methods were used to optimize the same neural-network parameterization of the policy.5
A
detailed listing of parameters used in the experiment is provided in Appendix E. We include the
classic cart-pole balancing task in additional to the more challenging locomotion domains, based on
the formulation from Barto et al. [24].
Learning curves of the policy optimization methods are shown in Figure 2. Our vine algorithm was
able to solve all of the tasks, learning a stable and naturalistic gait for the 2D hopper and walker.
The single path algorithm exhibits the best looking learning curves (the most reliably monotonic
improvement of total expected cost), but it did not yield a locomotion controller for the 2D walker;
instead, it yielded a controller that stood up but did not bother to move.
The cross-entropy method was not able to solve any of the tasks other than cart-pole, presumably
because it does not perform well for optimization problems with more than a couple dozen parame-
ters. Reward-weighted regression also performed reasonably well on the tasks, which is consistent
with the fact that it is performing gradient-based optimization of the policy, thus it can be expected
to scale with the number of parameters.6
We have also obtained promising preliminary results optimizing control policies for a 3D humanoid
model, which has 51 state dimensions and 19 actuators, using the single path algorithm. While the
initial policy falls over immediately, after several hundred iterations of policy iteration, we obtain a
policy that make substantial forward progress and survives for more than ten seconds before falling
over. Learning curves are shown in Figure 2.
Robot models in physics simulator
(MuJoCo, from Emo Todorov)](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-18-320.jpg)

![n Oqen simpler to represent good policies than good value func9ons
n True objec9ve of expected cost is op9mized (vs. a surrogate like Bellman error)
n Exis9ng work: (natural) policy gradients
n Challenges: good, large step direc9ons
Policy Op9miza9on
max
✓
E[
HX
t=0
R(st)|⇡✓]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-20-320.jpg)
![n Trust Region:
n Sampled evalua9on of gradient
n Gradient only locally a good approxima9on
n Change in policy changes state-ac9on visita9on frequencies
Trust Region Policy Op9miza9on
max
✓
E[
HX
t=0
R(st)|⇡✓]
[Schulman, Levine, Moritz, Jordan, Abbeel, 2015]
max
✓
ˆg>
✓
s.t. KL(P(⌧; ✓)||P(⌧; ✓ + ✓)) "](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-21-320.jpg)
![[Schulman, Levine, A.]
Experiments in Locomo9on](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-22-320.jpg)
![n Deep Q-Network (DQN) [Mnih et al, 2013/2015]
n Dagger with Monte Carlo Tree Search [Xiao-Xiao et al, 2014]
n Trust Region Policy Op9miza9on [Schulman, Levine, Moritz, Jordan, Abbeel, 2015]
Atari Games
Pong Enduro Beamrider Q*bert](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-25-320.jpg)
![n Generalized Advantage Es9ma9on
n Exponen9al interpola9on between actor-cri9c and Monte Carlo es9mates
n Trust region approach to (high-dimensional) value func9on es9ma9on
Generalized Advantage Es9ma9on (GAE)
max
✓
E[
HX
t=0
R(st)|⇡✓]
[Schulman, Moritz, Levine, Jordan, Abbeel, 2015]
Objec9ve:
Gradient:
single sample es9mate of advantage
E[
HX
t=0
r✓ log ⇡✓(at|st)
HX
k=t
R(sk) V (st)
!
]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-26-320.jpg)
![Learning Locomo9on
[Schulman, Moritz, Levine, Jordan, Abbeel, 2015]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-27-320.jpg)


![[Levine & Abbeel, NIPS 2014]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-32-320.jpg)



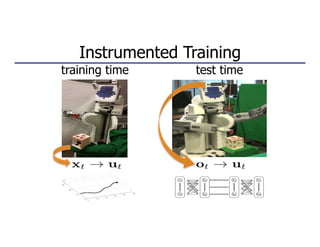
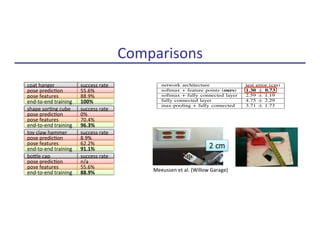
![Architecture (92,000 parameters)
[Levine*, Finn*, Darrell, Abbeel, 2015, TR at: rll.berkeley.edu/deeplearningrobo9cs]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-38-320.jpg)


![Learned Skills
[Levine*, Finn*, Darrell, Abbeel, 2015, TR at: rll.berkeley.edu/deeplearningrobo9cs]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-41-320.jpg)

![Visuomotor Learning Directly in Visual Space ?
Provide image that defines goal
Train controller in visual feature space
[Finn, Tan, Duan, Darrell, Levine, Abbeel, 2015]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-44-320.jpg)
![Visuomotor Learning Directly in Visual Space
1. Set target end-effector pose
2. Train exploratory non-vision controller
3. Learning visual features with collected images
4. Provide image that defines goal features
5. Train final controller in visual feature space
[Finn, Tan, Duan, Darrell, Levine, Abbeel, 2015]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-45-320.jpg)
![Visuomotor Learning Directly in Visual Space
[Finn, Tan, Duan, Darrell, Levine, Abbeel, 2015]](https://image.slidesharecdn.com/makingrobotslearn-170825150605/85/Making-Robots-Learn-46-320.jpg)