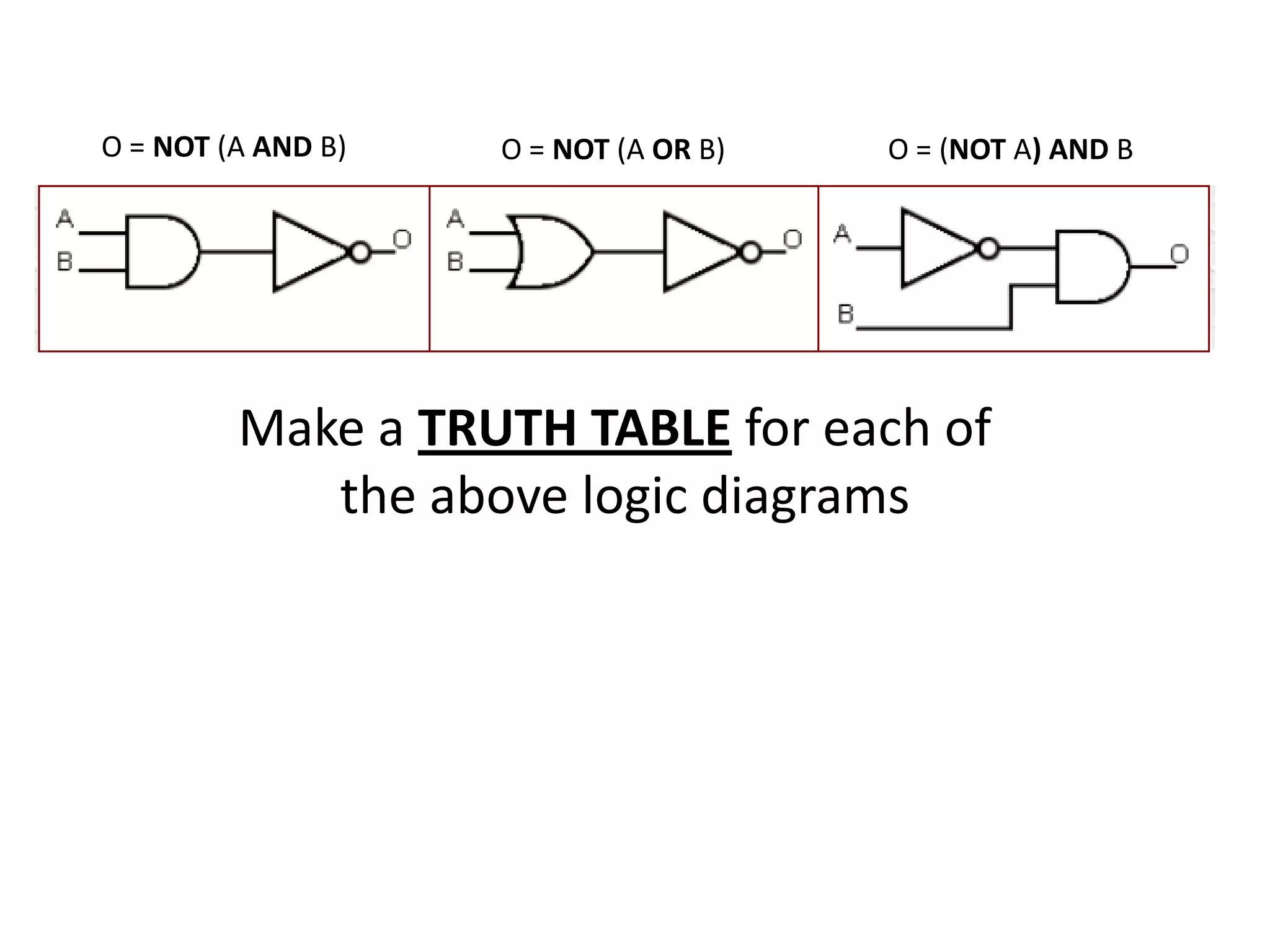
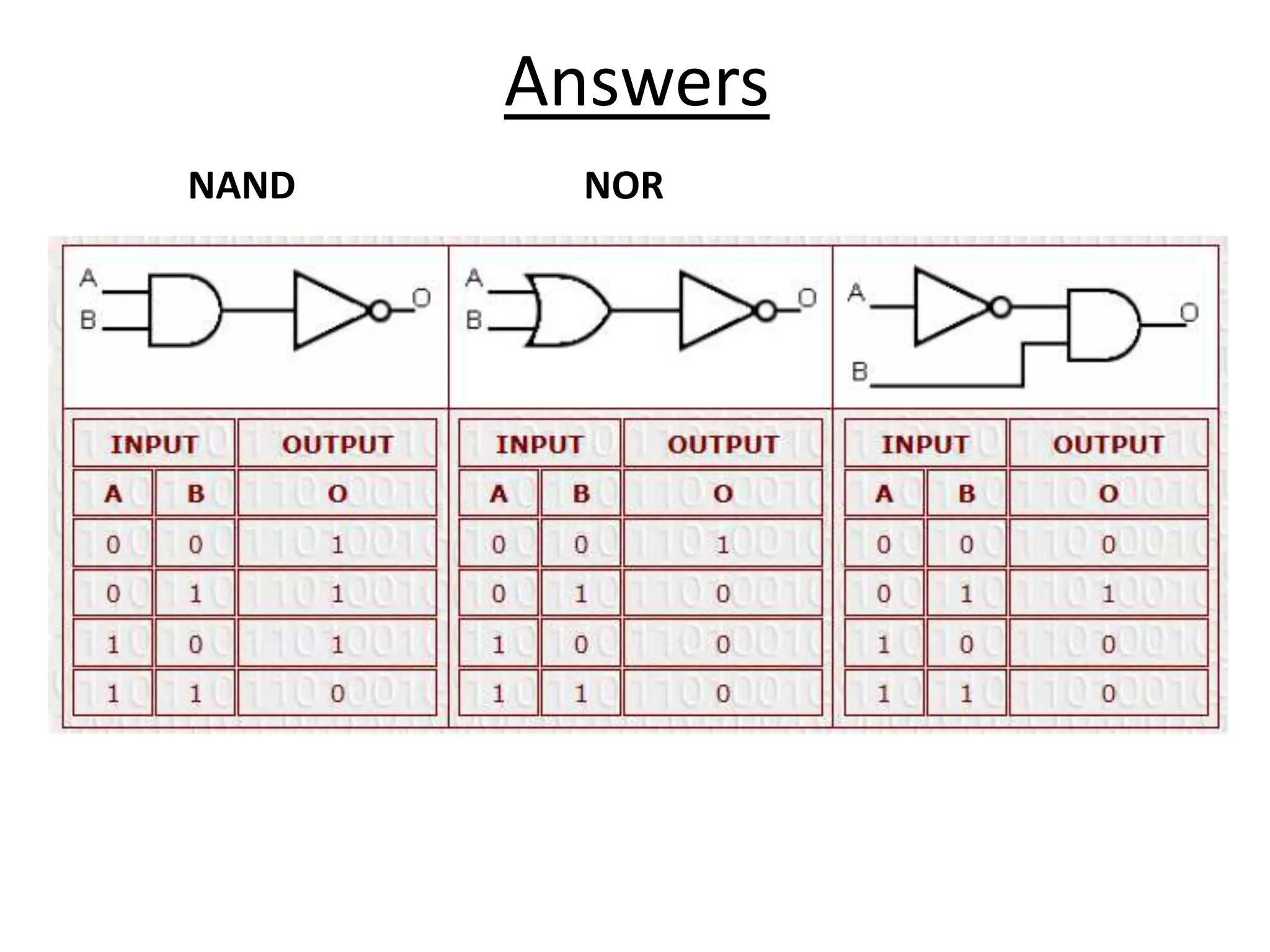
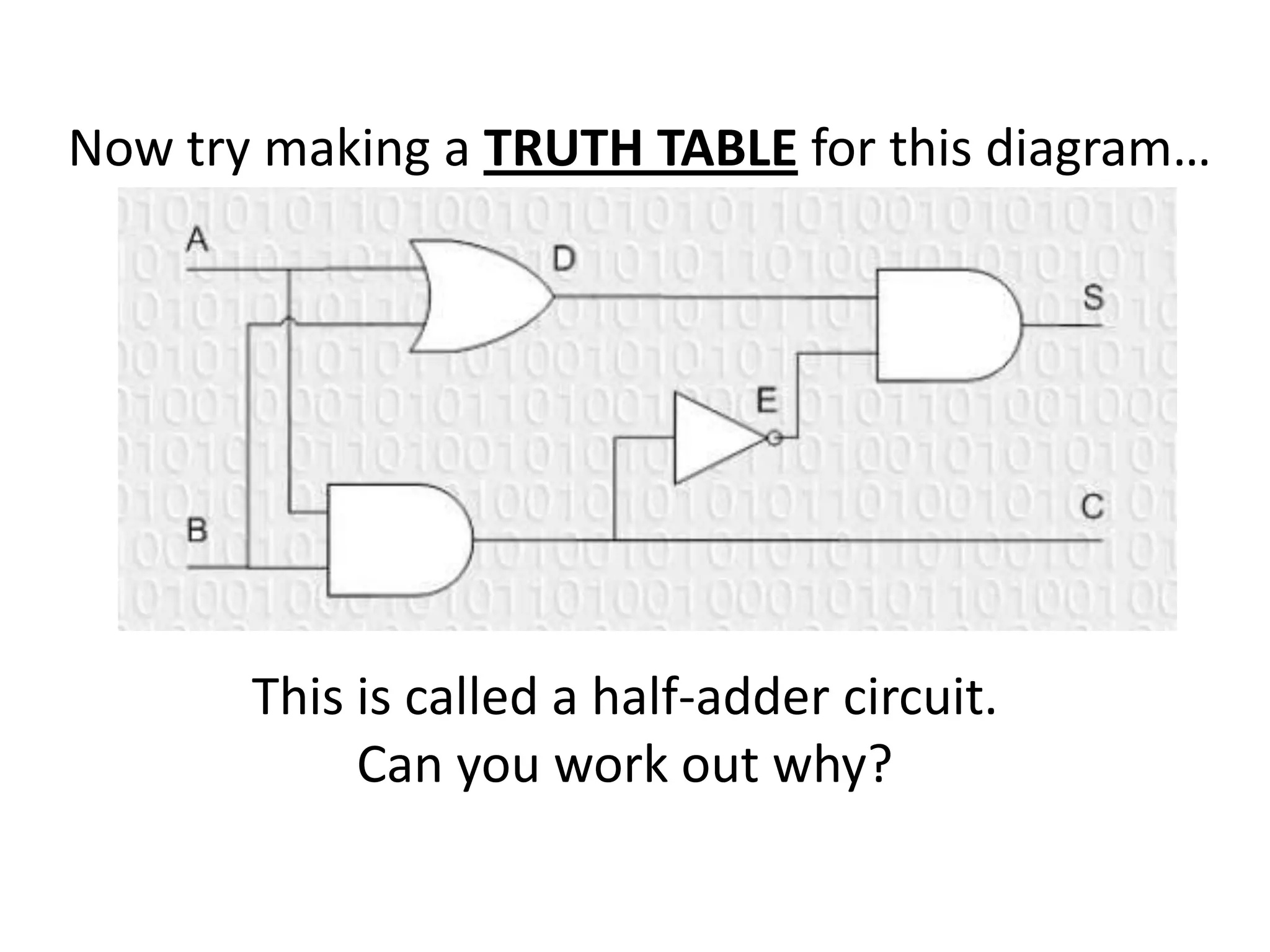
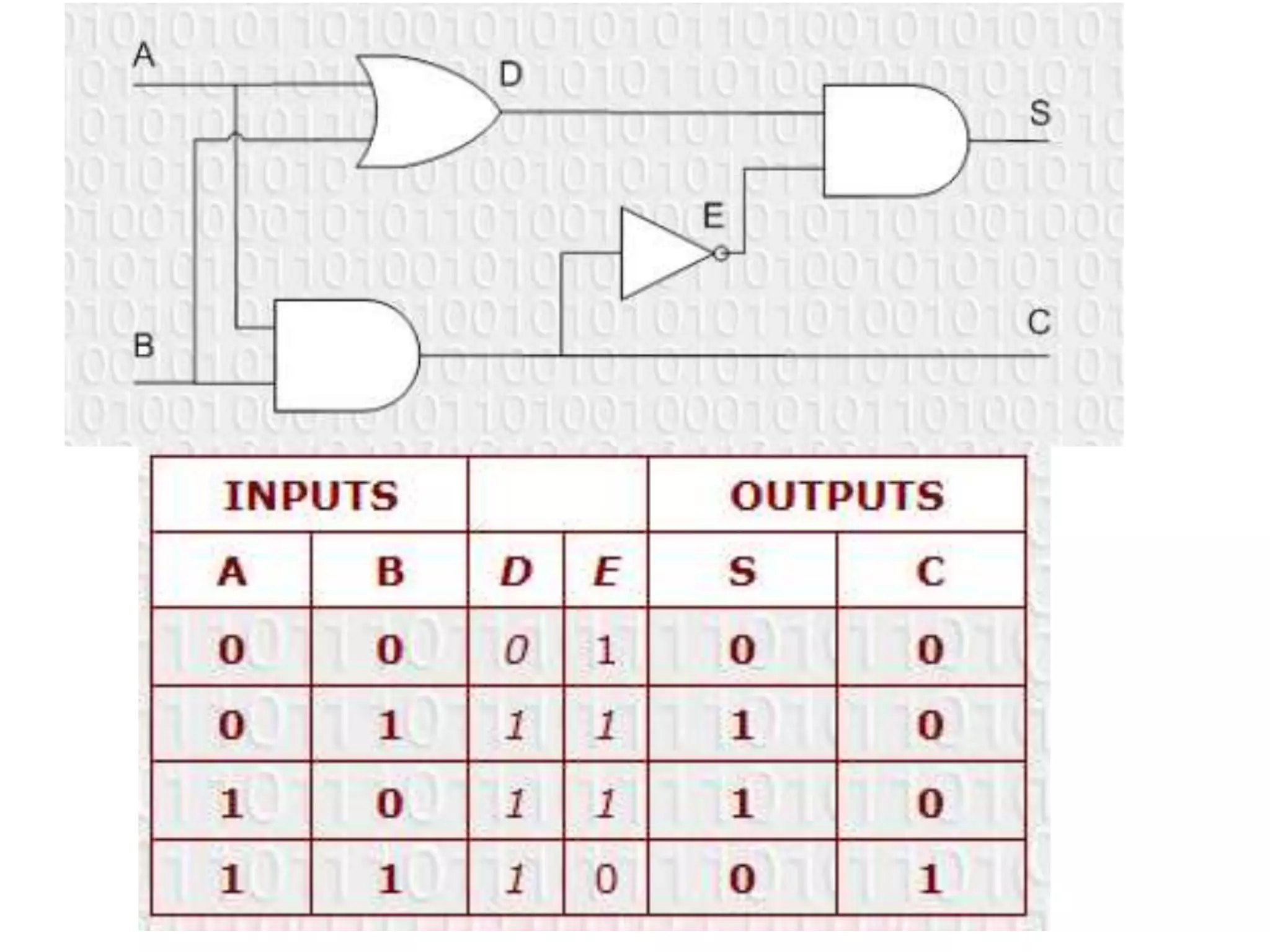
The document discusses logic diagrams and truth tables. It explains that to produce a truth table, you need to determine the outputs for every possible combination of inputs. The number of combinations is 2 to the power of the number of inputs. It then asks the reader to make a truth table for a half-adder circuit, which is designed to add two binary numbers and output a sum and carry value based on logic statements.

1. O = NOT (A AND B) O = NOT (A OR B) O = (NOT A) AND B
Make a TRUTH TABLE for each of
the above logic diagrams

2. Answers
NAND NOR

3. More about logic tables
• To produce a truth table from a logic diagram you need to
work out the outputs for every possible combination of
inputs.
– If a logic diagram has only 2 inputs then there will only be 4 input
combinations (00, 01, 10 and 11).
– If there are 3 inputs then there will be 8 possible combinations.
– 4 inputs would give 16 combinations.
• Therefore n inputs gives 2n outputs

4. Now try making a TRUTH TABLE for this diagram…
This is called a half-adder circuit.
Can you work out why?

5. Half-adder Circuit
• Are designed to add 2 binary numbers with a
carry (C) if the sum (S) is greater than 1.
• So this can be expressed as a logic statement:
S = (A OR B) AND (NOT (A AND B))
C = (A AND B)