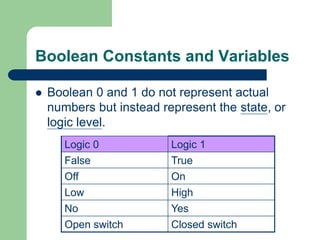
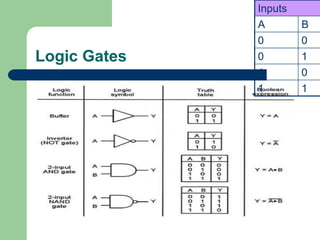
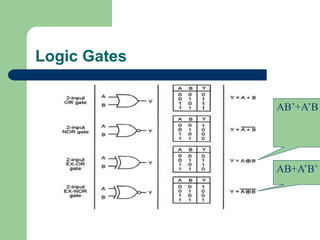
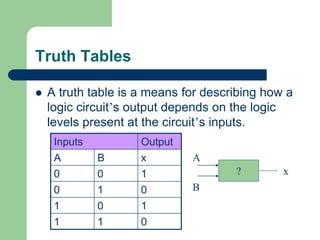
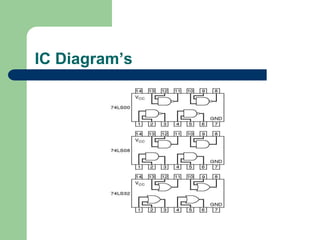
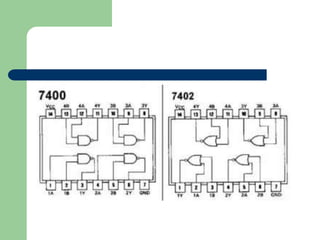
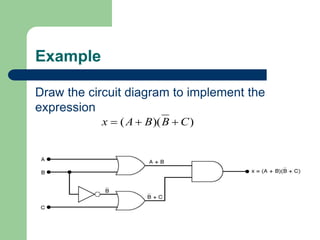
This document discusses digital logic gates and Boolean algebra. It defines the objectives as performing basic logic operations, describing AND, NAND, OR and NOR gates using truth tables, writing Boolean expressions, and implementing logic circuits. It explains Boolean constants and variables, the three basic logic operations (OR, AND, NOT), logic gates and their truth tables, gate IC numbers, and gives examples of implementing Boolean expressions as logic circuits.

1. Digital Systems
Logic Gates and Boolean Algebra

2. Objectives
 Perform the three basic logic operations.
 Describe the operation of and construct the truth tables
for the AND, NAND, OR, and NOR gates, and the NOT
(INVERTER) circuit.
 Write the Boolean expression for the logic gates and
combinations of logic gates.
 Implement logic circuits using basic AND, OR, and
NOT gates.

3. Objectives
 Use either of the universal gates (NAND or NOR) to
implement a circuit represented by a Boolean
expression.
 Explain the advantages of constructing a logic-circuit
diagram using the alternate gate symbols versus the
standard logic-gate symbols.
 Describe the concept of active-LOW and active-HIGH
logic symbols.

4. Boolean Constants and Variables
 Boolean 0 and 1 do not represent actual
numbers but instead represent the state, or
logic level.
Logic 0 Logic 1
False True
Off On
Low High
No Yes
Open switch Closed switch

5. Three Basic Logic Operations
 OR
 AND
 NOT

6. Logic Gates
Inputs
A B
0 0
0 1
1 0
1 1

7. Logic Gates
AB’+A’B
AB+A’B’

8.  IN CASE OF NOT GATE OUTPUT IS NOT AS
INPUT.
 IN CASE OF AND GATE, OUTPUT WILL BE
ONE IF A AND B, ARE ONE
 IN THE CASE OF OR GATE, OUTPUT WILL
BE ONE IF A OR B IS ONE.

9. Truth Tables
 A truth table is a means for describing how a
logic circuit’s output depends on the logic
levels present at the circuit’s inputs.
Inputs Output
A B x
0 0 1
0 1 0
1 0 1
1 1 0
?
A
B
x

10. Logic Gates and there IC numbers
 AND – IC 7408
 OR – IC 7432
 NOT – IC 7404
 NOR – IC7402
 NAND – IC 7400
 XOR – IC 7486

11. IC Diagram’s

13. Poll Questions
Q1. What is the IC number of NAND gate?
a) 7408
b) 7402
c) 7400
d) 7404

14. Poll Question
Q2. If both the inputs of OR gate are high then
what will be the output?
a) 0
b) 1
c) Both a and b
d) None of these

15. Poll Question
Q3. The logic gate that will have HIGH or "1" at its output
when any one of its inputs is HIGH
a) NOR gate
b) AND gate
c) OR gate
d) NOT operation

16. Implement the following:
(a) AB+A’C+BC = AB+A’C

17. Example
Draw the circuit diagram to implement the
expression
)
)(
( C
B
B
A
x 

