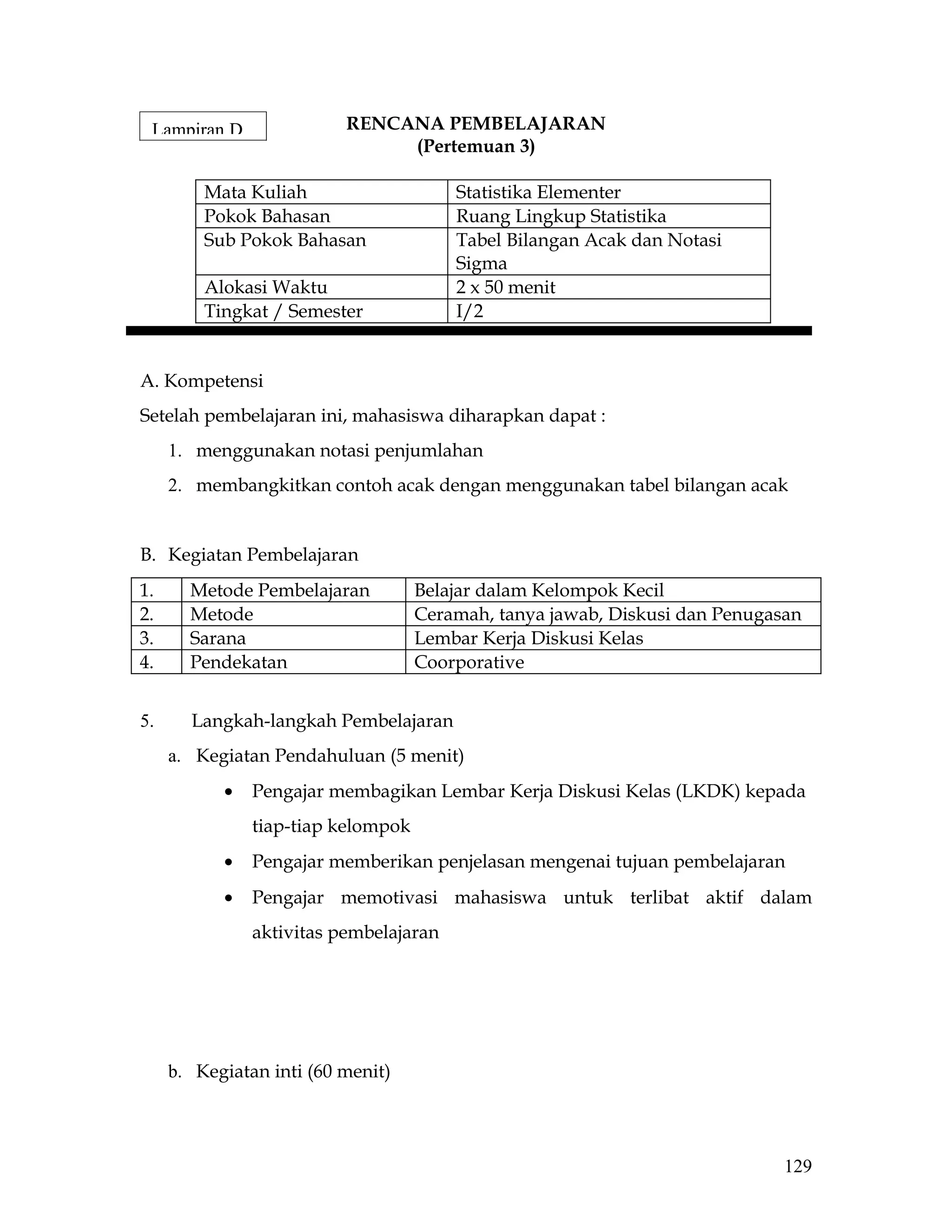
Dokumen ini adalah rencana pembelajaran pertemuan ketiga mata kuliah statistika elementer yang mencakup topik tabel bilangan acak dan notasi sigma. Mahasiswa diharapkan dapat menggunakan notasi penjumlahan dan membangkitkan contoh acak melalui diskusi kelompok dan bimbingan pengajar. Rencana juga termasuk kegiatan penutup dengan latihan soal individu dan kelompok untuk menguji pemahaman siswa.

1. Lampiran D RENCANA PEMBELAJARAN
(Pertemuan 3)
Mata Kuliah Statistika Elementer
Pokok Bahasan Ruang Lingkup Statistika
Sub Pokok Bahasan Tabel Bilangan Acak dan Notasi
Sigma
Alokasi Waktu 2 x 50 menit
Tingkat / Semester I/2
A. Kompetensi
Setelah pembelajaran ini, mahasiswa diharapkan dapat :
1. menggunakan notasi penjumlahan
2. membangkitkan contoh acak dengan menggunakan tabel bilangan acak
B. Kegiatan Pembelajaran
1. Metode Pembelajaran Belajar dalam Kelompok Kecil
2. Metode Ceramah, tanya jawab, Diskusi dan Penugasan
3. Sarana Lembar Kerja Diskusi Kelas
4. Pendekatan Coorporative
5. Langkah-langkah Pembelajaran
a. Kegiatan Pendahuluan (5 menit)
• Pengajar membagikan Lembar Kerja Diskusi Kelas (LKDK) kepada
tiap-tiap kelompok
• Pengajar memberikan penjelasan mengenai tujuan pembelajaran
• Pengajar memotivasi mahasiswa untuk terlibat aktif dalam
aktivitas pembelajaran
b. Kegiatan inti (60 menit)
129

2. Putaran Pertama
• Pengajar mempersilakan masing-masing kelompok untuk mengisi
LKDK bagian A. Selama diskusi berlangsung, pengajar memantau
jalannya diskusi semua kelompok dengan berkeliling dan
memberikan pengarahan kepada kelompok yang mengalami
kesulitan.
• Pengajar meminta beberapa orang mahasiswa sebagai wakil
kelompoknya untuk menyampaikan hasil diskusi kelompoknya.
Mahasiswa dari kelompok lain memberikan tanggapannya
mengenai hasil kelompok tersebut (sharing ideas). Dari hasil diskusi
kelas tersebut, pengajar memberikan bimbingan mengenai
penggunaan notasi penjumlahan.
Putaran Kedua
• Pengajar mempersilakan masing-masing kelompok untuk mengisi
LKDK bagian B. Selama diskusi kelas berlangsung, pengajar
memantau diskusi kelompok tersebut dengan berkeliling. Pengajar
juga mengarahkan kelompok-kelompok yang mengalami kesulitan.
• Pengajar meminta beberapa orang mahasiswa untuk
menyampaikan hasil kerjanya. Mahasiswa dari kelompok lain
memberikan tanggapannya. Dari hasil diskusi kelas tersebut,
pengajar memberikan bimbingan memperoleh hasil yang benar
untuk LKDK bagian B tersebut
c. Kegiatan Penutup ( 10 menit)
130

3. • Pengajar menyampaikan kesimpulan mengenai notasi
penjumlahan dan penggunaan tabel acak.
• Pengajar memberikan soal latihan untuk dikerjakan secara
individual, yaitu soal pada LKDK bagian C nomor 1 dan 3.
• Pengajar memberikan soal latihan 1untuk dikerjakan secara
berkelompok, yaitu soal pada LKDK bagian C nomor 2 dan 4.
131

4. LEMBAR KERJA
DISKUSI KELAS
(LKDK)
A. Tabel bilangan Acak
1. Sebutkan beberapa cara untuk membangkitkan bilangan acak.
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
2. Diskusikan membangkitkan data cara menggunakan tabel acak untuk
membangkitkan data jika :
a. N = 1000, n = 50
b. N = 500, n = 50
c. N = 300, n = 50
B. Notasi Penjumlahan
1. Uraikan :
n
a. ∑x
i =1
i = ....................................................................................................................
n
b. ∑ x = ......................................................................................................................
i =1
n
c. ∑ i = ......................................................................................................................
i =1
n
d. ∑ 3x
i =1
i = ..................................................................................................................
132

5. n
e. ∑ (x
i =1
2
i − 3 xi ) = ........................................................................................................
n
f. ∑x y
i =1
i i = .................................................................................................................
n m
g. ∑∑ x y
i =1 j =1
i i = .............................................................................................................
2. Diketahui x1 = 3, x2 = 5, x3 = 6, y1 = 2, y2 = 8 dan y3 = 2. Tentukan :
2
a. ∑x
i =1
i = ....................................................................................................................
4
b. ∑ 3 = ......................................................................................................................
i =1
3
c. ∑ 3x
i =1
i = ..................................................................................................................
3
d. ∑ (x
i=2
2
i − 3 x i ) = ........................................................................................................
3
e. ∑x y
i =1
i i = .................................................................................................................
3 3
f. ∑∑ x y
i =1 j =1
i i = .............................................................................................................
C. Soal-soal Latihan
1. (Tugas individu) Bagian SDM sebuah perusahaan akan melakukan penelitian
mengenai opini karyawannya mengenai kebijakan-kebijakan manajemen
perusahaan. Bila perusahaan tersebut memiliki 650 karyawan (dilabelkan
dengan karyawan 1 sampai karyawan 650) dan dalam penelitian tersebut,
bagian SDM hanya ingin mengambil 20 karyawan sebagai sampel. Bila
dalam pemilihan, peneliti SDM menggunakan tabel acak dan memulai
pengacakan dari baris 25 kolom 31 (ke arah bawah), tentukan karyawan
yang terpilih.
133

6. 2. (Tugas kelompok) Seorang mahasiswa tingkat akhir Jurusan Matematika akan
mengadakan penelitian mengenai rata-rata pengeluaran mingguan
mahasiswa Jurusan Matematika. Dari 300 orang mahasiswa, ia akan
mengambil contoh acak sebanyak 50 orang.
a. Tentukan populasi, contoh, parameter dan statistik pada penelitian
tersebut.
b. Dengan memberikan nomor 1 sampai 300 pada semua mahasiswa,
mahasiswa mana saja yang terpilih bila pada Tabel Bilangan Acak
bila ia memulai pengacakan pada baris 25 kolom 31 ke arah bawah
3. (Tugas individu) Buktikan bahwa :
n n n n
a. ∑ ( xi + yi + zi ) =∑ xi +∑ yi +∑ zi
i =1 i =1 i =1 i =1
n n
b. ∑ ( cxi ) = c∑ xi
i =1 i =1
dengan c adalah konstanta
n
c. Bila c adalah konstanta, maka ∑ c = nc
i =1
4. (Tugas kelompok) Buktikan bahwa :
∑∑ ( x + y ij + z ij ) = ∑∑ xij + ∑∑ y ij + ∑∑ z ij
m n m n m n m n
a. ij
i =1 j =1 i =1 j =1 i =1 j =1 i =1 j =1
b. ∑∑ ( cx ) = c ∑∑ x
m n m n
ij ij
i =1 j =1 i =1 j =1
m n
c. ∑∑ c = mnc
i =1 j =1
m n
 m  n 
d. ∑∑
i =1 j =1
xi y j =  ∑ xi  ∑ y j 

 i =1  j =1 

134