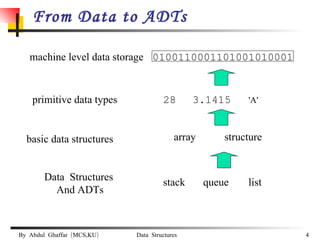
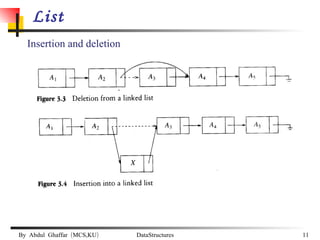
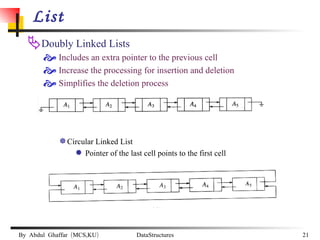
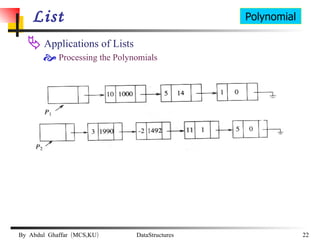
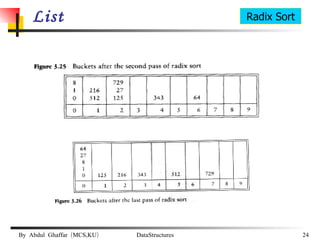
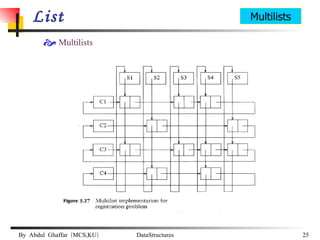
The document discusses data structures and abstract data types (ADTs). It provides examples of common ADTs like lists, trees, stacks, and graphs. It specifically focuses on lists, describing two common implementations of lists as arrays and linked lists. It discusses the advantages and disadvantages of each implementation and provides examples of common list operations like insertion, deletion, and searching.

1. Data Structures and Algorithm Analysis By Abdul Ghaffar (MCS, KU)

2. Reference Books Data Structures and Algorithm Analysis in C By Mark Allen Weiss Published by Addison Wesley Data Structures (Schaum’s Outline Series) By Seymour Lipschutz Published by Mc Graw Hill

3. Abstract Data Types (ADT) Definition: An Abstract Data Type is a mathematical abstraction of an organization of data and a set of operations to implement on the ADT. Basic Idea: Implement the operation once and use them anywhere in the program to perform the operation any number of times. There is no rule telling which operation must be supported for each ADT. This is a design Decision. Examples: Data Types Integer, Real, Bool, Character ADTs Lists, Trees, Stacks, Sets, Graphs

4. From Data to ADTs machine level data storage primitive data types basic data structures Data Structures And ADTs 0100110001101001010001 28 3.1415 'A' stack queue list array structure

5. L I S T S Based on Chapter 3 Of Reference Book #1

6. List The List Model The form of the List is as Al, A2, A3, AN The size of this list is N. An empty list is a special list of size 0 . For any list except the empty list, w say the t Ai+1 follows (or succeeds) Ai (i < N) and that Ai-1 precedes Ai (i > 1). The first element of the list is Al, and the last element is AN. The predecessor of Al or the successor of AN will not be defined. The position of element Ai in a list is i. Set of operations printList MakeEmpty Find ‘ returns the position of e firs-t occurrence of a key Insert and Delete ‘ insert and delete some key from some position FindKth ‘ which returns the element in some position

7. List Example: If the list is 34, 12, 52, 16, 12 then Find(52) might return 3 Insert(X, 3) might make the list into 34, 12, 52, X, 16, 12 (if we insert after the position given) Delete(52) might turn that list into 34, 12, X, 16, 12. Notes: What is appropriate for a function is entirely up to the programmer We could also add operations such as Next and Pmvious , which would take a position as argument and return the position of the successor and predecessor, respectively.

8. List Implementations As an Array Limitations Size of the list must be known in advance May cause wastage of the memory space Deletion and insertion are difficult Advantages Implementation is easy Searching and Traversing is easy

9. List As Linked list Definition: The linked list consists of a series of structures, which are not necessarily adjacent in memory. Each structure contains the element and a pointer to a structure containing its successor. NULL

10. List Advantages Less memory is required List can be dynamic, so there no need to know the size in advance Insertion and deletion are easy Disadvantages Implementation is comparably difficult Requires more processing

11. List Insertion and deletion

12. List Programming Details Some Problems No way to insert at, and delete the elements from the front For deletion keep record for the previous element of the deleted item Solutions Use Header or dummy node Build a routine FindPrevious

13. Example:- Declarations: List ADT

14. Example:- Declarations: List ADT

15. Example:- Function to test if The List is empty Function to test last position List ADT

16. Example:- Find routine List ADT

17. Example:- Deletion Routine for a item X List ADT

18. Example:- Find Previous Routine List ADT

19. Example:- Insertion Routine List ADT

20. Example:- Delete List routine List ADT

21. List Doubly Linked Lists Includes an extra pointer to the previous cell Increase the processing for insertion and deletion Simplifies the deletion process Circular Linked List Pointer of the last cell points to the first cell

22. List Applications of Lists Processing the Polynomials Polynomial

23. List Applications of Lists Radix Sort (Example) : Initial data -> 64, 8, 216, 512, 27, 729, 0, 1, 343, 125 Radix Sort

24. List Radix Sort

25. List Multilists Multilists