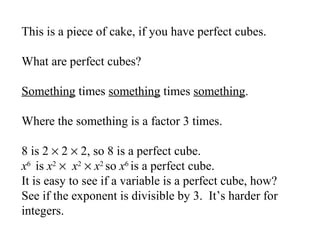This document discusses factoring the sum and difference of two cubes. It explains that the sum or difference of two cubes can be factored into a binomial times a trinomial, with the first term of the trinomial being the cube root of the first term, the second term being the product of the cube roots, and the third term being the cube root of the second term. It provides an example of factoring 27x3 - 125 to show the process.

1. Factoring the Sum & Difference
of Two Cubes
p.368-371

2. This is a piece of cake, if you have perfect cubes.
What are perfect cubes?

3. This is a piece of cake, if you have perfect cubes.
What are perfect cubes?
Something times something times something.
Where the something is a factor 3 times.
8 is 2 × 2 × 2, so 8 is a perfect cube.
x6 is x2 × x2 × x2 so x6 is a perfect cube.
It is easy to see if a variable is a perfect cube, how?

4. This is a piece of cake, if you have perfect cubes.
What are perfect cubes?
Something times something times something.
Where the something is a factor 3 times.
8 is 2 × 2 × 2, so 8 is a perfect cube.
x6 is x2 × x2 × x2 so x6 is a perfect cube.
It is easy to see if a variable is a perfect cube, how?
See if the exponent is divisible by 3. It’s harder for
integers.

5. The sum or difference of two cubes will factor into a
binomial × trinomial.
(
a + b = ( a + b ) a − ab + b
3
3
2
2
)
same sign
always +
always opposite
(
a − b = ( a − b ) a + ab + b
3
3
same sign
always opposite
2
2
)
always +

6. Now we know how to get the signs, let’s work on
what goes inside.
Square this term to get this term.
(
a + b = ( a + b ) a − ab + b
3
3
2
2
)
Cube root of 1st term
Cube root of 2nd term
Product of cube root of 1st term
and cube root of 2nd term.

7. Try one.
27 x −125 =
3
Make a binomial and a trinomial
with the correct signs.

8. Try one.
27 x −125 =
3
(
−
Cube root of 1st term
)(
+
+
)
Cube root of 2nd term

9. Try one.
27 x −125 = ( 3x − 5)(
3
+
+
)
Square this term to get this term.

10. Try one.
27 x −125 = ( 3x − 5) ( 9 x 2 +
3
+
)
Multiply 3x an 5 to get this term.

11. Try one.
27 x −125 = ( 3x − 5) ( 9 x + 15 x +
3
2
Square this term to get this term.
)

12. Try one.
(
27 x −125 = ( 3 x − 5) 9 x + 15 x + 25
3
2
)
You did it!
Don’t forget the first rule of factoring is to look
for the greatest common factor.