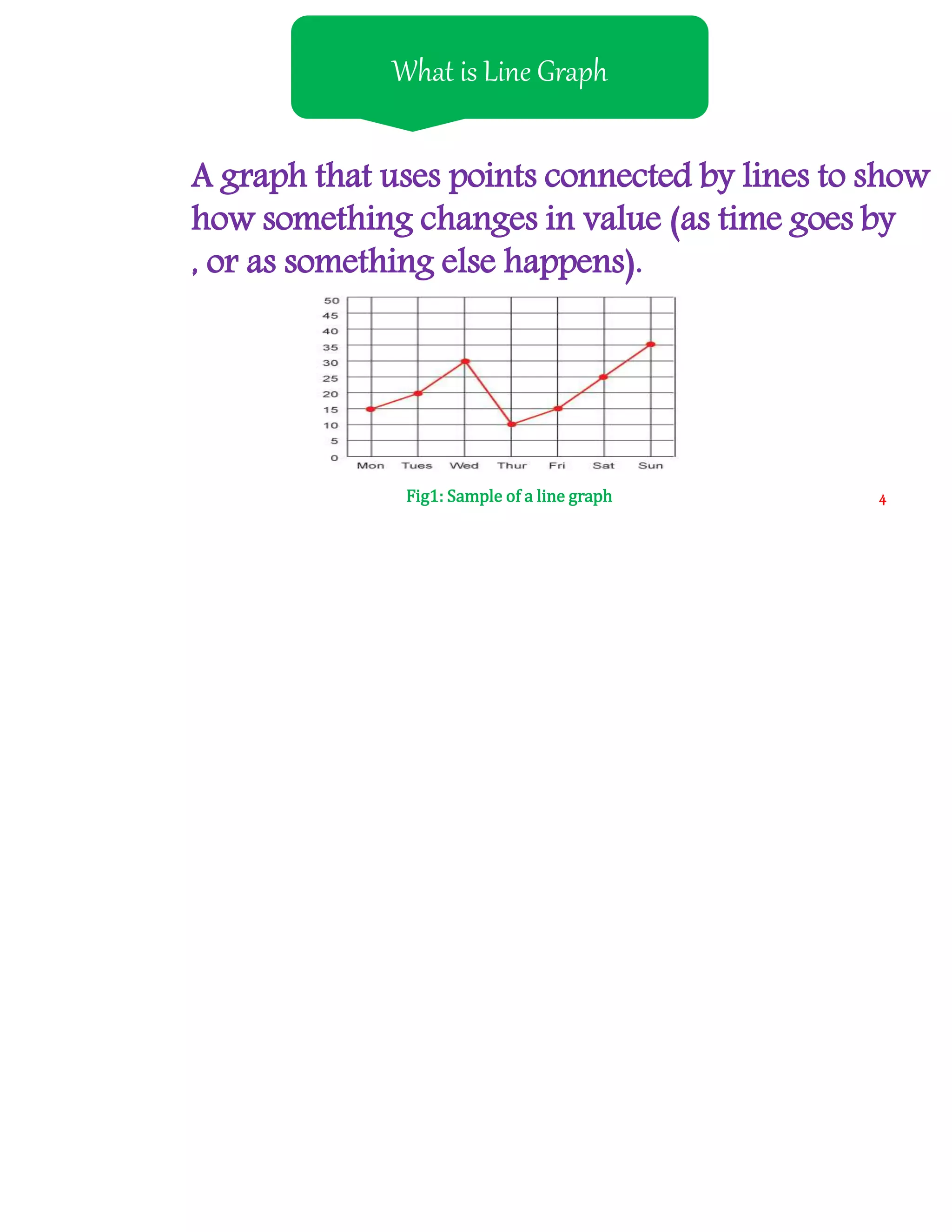
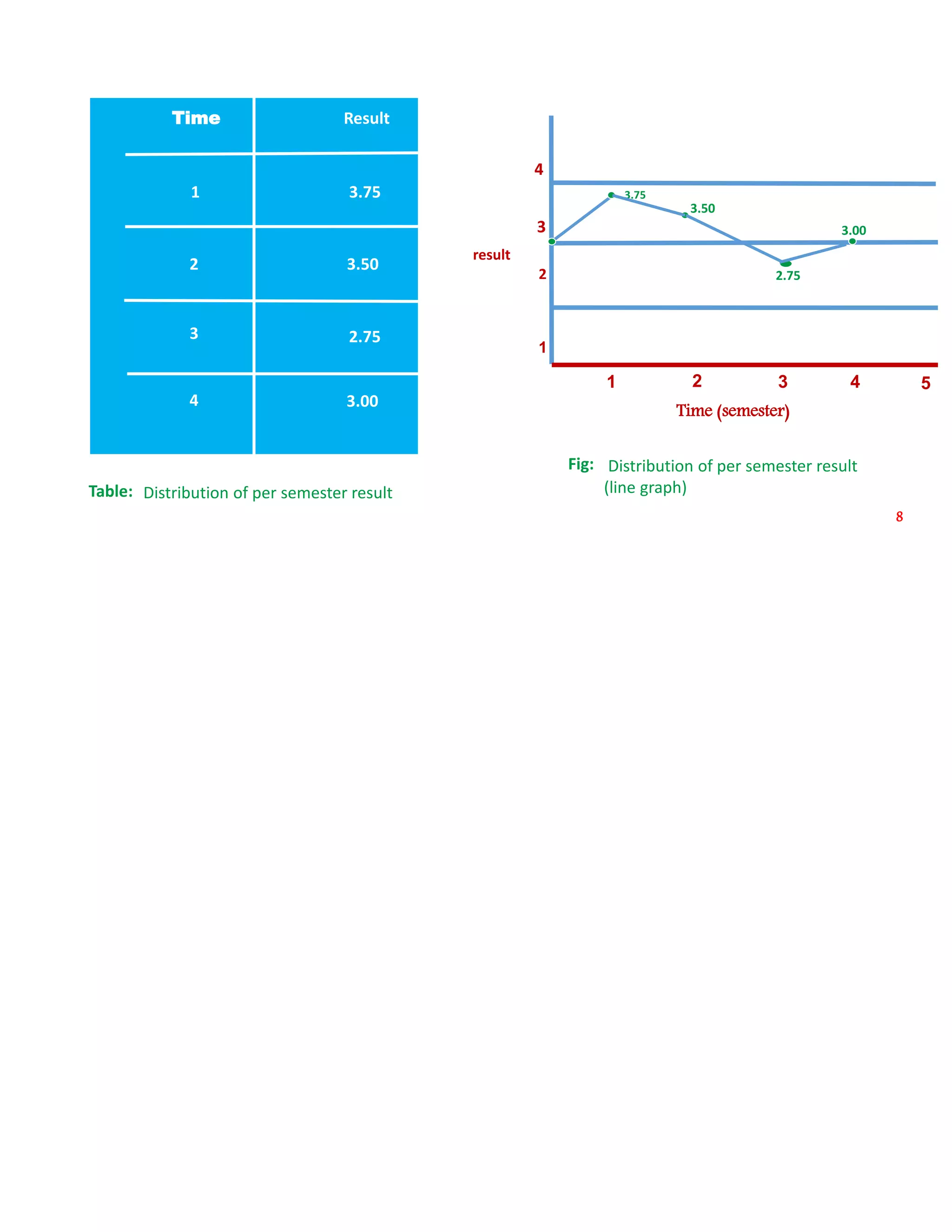
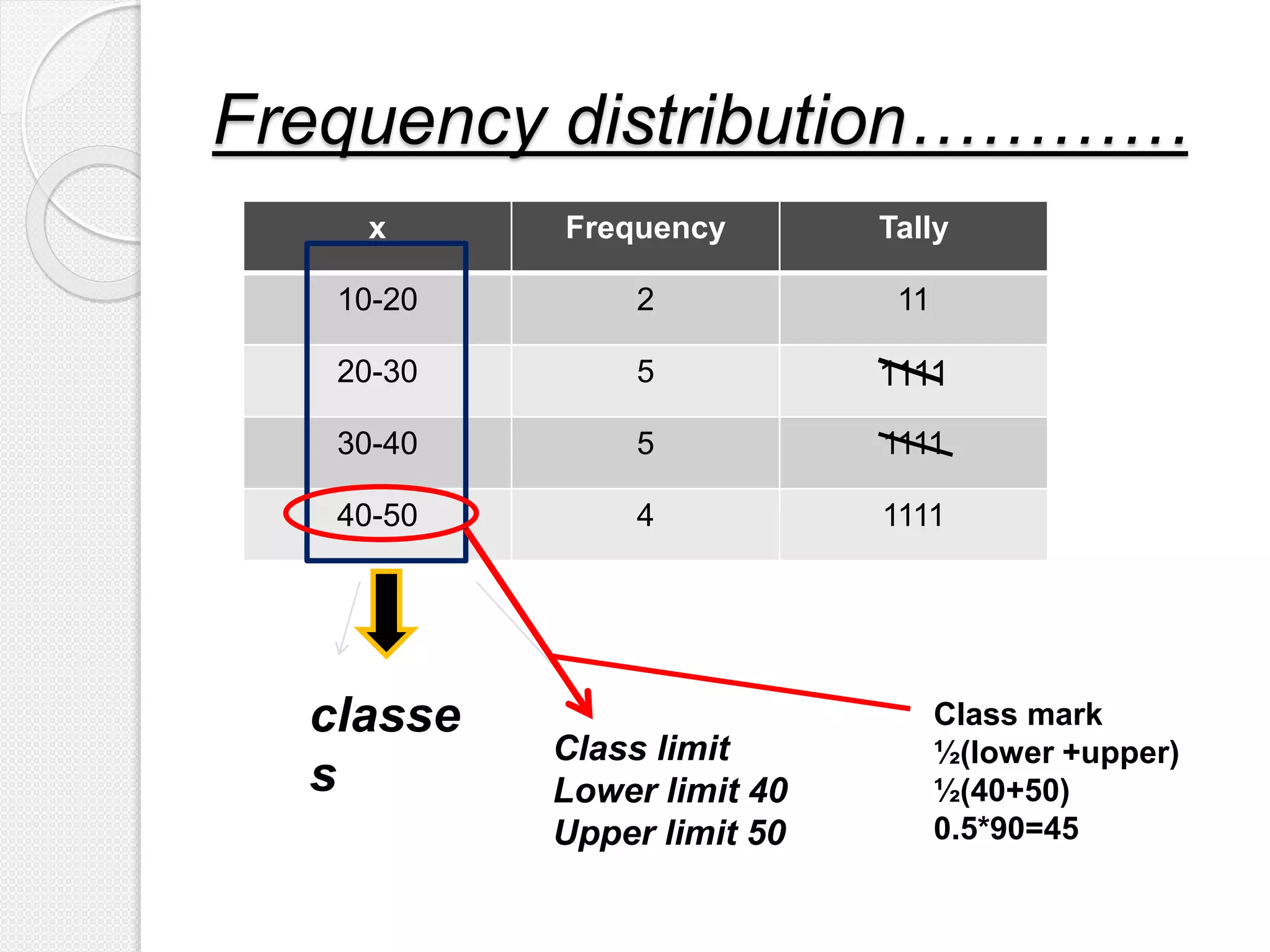
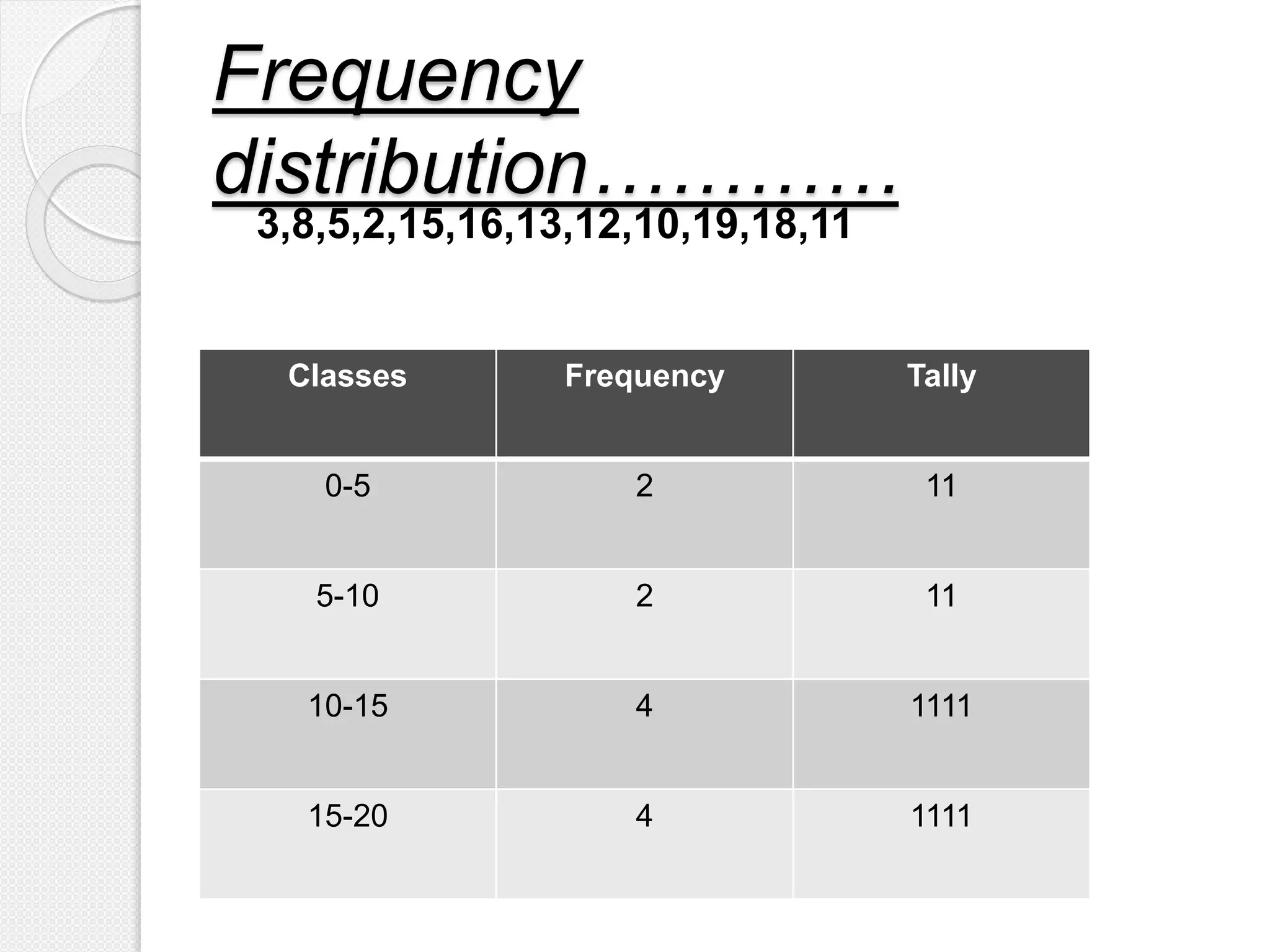
The document discusses line graphs and frequency distributions. 1) A line graph uses points connected by lines to show how a value changes over time or as another variable changes. Line graphs are used to track qualitative data and compare changes over time for multiple groups. 2) A frequency distribution organizes data into classes and counts the frequency of observations in each class. It can group or ungroup data. The distribution includes the class, frequency, and tally marks.

1. Line Graph

2. What is Line Graph
A graph that uses points connected by lines to show
how something changes in value (as time goes by
, or as something else happens).
Fig1: Sample of a line graph 4

3. Line graphs are used for “qualitative data”. Line graphs are
used to track changes over short and long periods of time.
When smaller changes exist, line graphs are better to use.
Line graphs can also be used to compare changes over the
same period of time for more than one group.
What is a line graph used for
5

4. • Qualitative data is information about qualities;
information that can't actually be measured.
• Example:
 Hair Color
 Softness Of Skin
 Gender
About Qualitative Data
6

5. Line Graph
Draw a line for your x axis and your y axis.
Add axis labels and an axis scale.
Mark your data points.
Draw a line through the data points.
Add a chart title.
7

6. 1
2
3
4
1 2 3 4 5
Time (semester)
result
3.75
3.50
2.75
3.00
Time Result
1
2
3
4
3.75
3.50
2.75
3.00
Fig:
Table:
8
Distribution of per semester result
(line graph)Distribution of per semester result

7. Scatter Diagram:
The simplest method of investigating the relationship
between two variables is to plot a scatter diagram
Let there will be two series ‘x’ (Independent Variable) and
‘y’ (Dependent Variable) to be represented graphically.
Take the items in ‘x’ series along the axis of ‘x’ and the
corresponding items in ‘y’ series along the y-axis. The
diagram so formed will be a dotted one and scattered,
showing some relationship, such a diagram is called a
scattered.

8. Scatter diagram can be used to find that there is any
correlation between the variable, whether the correlation
is linear or non- linear and whether it is positive or
negative.
Interpretation of correlation is done in the following ways.

9. Linear Correlation:-
If all the points on the scatter diagram tend to lie near a line,
the correlation is said to be linear.

10. Curvi Linear Correlation:-
If all the points on the scatter diagram tend to lie near
a smooth curve (not a straight line) the correlation is
said to be curvilinear.

11. Positive Linear Correlation:-
If all the points tend to lie near an upward sloping line ,
the linear correlation is said to be positive correlation.

12. Negative Linear Correlation:-
If all the points tend to lie on a downward sloping line,
the linear correlation is said to be negative correlation.

13. Perfect Positive Correlation:-
If all the points tend to lie on an upward sloping line
the correlation is perfectly positive correlation.

14. Perfect Negative Correlation:-
If all the points tend to lie on a downward sloping line the
correlation is perfectly negative correlation.

15. Null Correlation:-
If the points on a scatter diagram do not show a definite
movement then there is no correlation between the variables.

16. Frequency
Distribution
Grouped & Ungrouped
NOUFALNAHEEM KK
MTTM

17. Frequency
distribution…………
 Is a statistical method for summarizing
the data’s.
It orderly arranging data's, after
collecting.
when the data are grouped into
classes of appropriate size indicating
the number of observations in each
class we get a frequency distribution.

18. Frequency
distribution…………
 A statistical data consist of a list of
numbers related to a research, among
those numbers , few may be repeated
twice and more than twice.
 The repeating numbers in a data set is
termed as ‘frequency’; that
frequencies are listed in a table is
known as ‘frequency
distribution/table’.

19. Frequency
distribution…………
 Objectives
 1-To estimate the frequencies of the
population .
 2-To facilitate the analysis of data.
 3-To facilitate computation of various
statistical measures.

20. Frequency distribution…………
 Components ……
 1-class
 Groups according to size of data.
 2-class limit
 The smallest and largest possible
measurements in each classes.
 *lower limit
 *upper limit

21. Frequency distribution…………
 3-class mark
 Also known as middle value.
 ½(lower limit + upper limit)
 4-Class interval
 Upper limit - lower limit
5-class boundaries

22. Frequency
distribution…………
 6-Class frequency
 The number observations falling in
each class.
 7-Tally mark
 Strokes against each frequency
observed.

23. Frequency distribution…………
x Frequency Tally
10-20 2 11
20-30 5 1111
30-40 5 1111
40-50 4 1111
classe
s
Class limit
Lower limit 40
Upper limit 50
Class mark
½(lower +upper)
½(40+50)
0.5*90=45

24. Frequency distribution…………
 Grouped frequency distribution.
 based on classes, forming frequency
distribution table.
 Example:
 From the following data construct a
grouped frequency distribution.
 3,8,5,2,15,16,13,12,10,19,18,11

25. Frequency
distribution…………
Classes Frequency Tally
0-5 2 11
5-10 2 11
10-15 4 1111
15-20 4 1111
3,8,5,2,15,16,13,12,10,19,18,11

26. Frequency distribution…………
 Ungrouped frequency distribution
 These data’s not arranged in
group, the are individual series. it
arranging in ascending order.
 Example:
 From the following ,make a ungrouped
frequency distribution.
 11,12,5,3,11,13,17,13,5,5,11,5

27. Frequency distribution…………
 11,12,5,3,11,13,17,13,5,5,11,5
X Frequency Tally
3 1 1
5 4 1111
11 3 111
12 1 1
13 2 11
17 1 1

28. NOUFALNAHEEM KK
MTTM