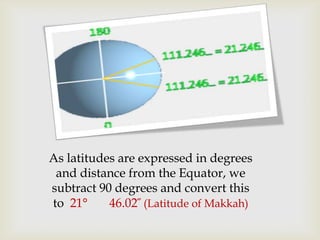
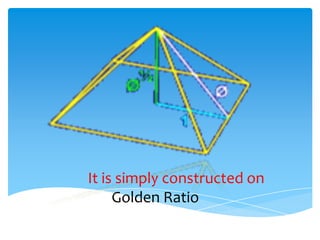
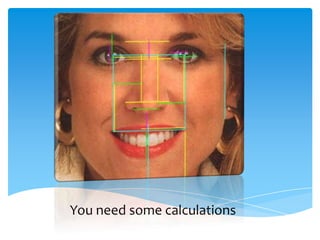
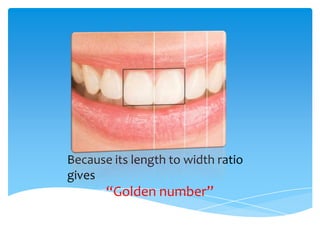
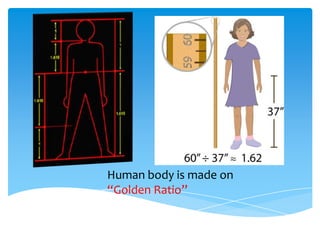
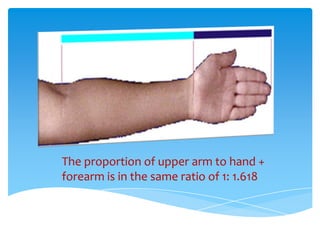
The document explores the Fibonacci sequence and its relation to the golden ratio, highlighting how this mathematical concept appears in nature and art. It discusses examples such as flower spirals, DNA structure, and historical architecture, including the Great Pyramid and the Taj Mahal, that utilize the golden ratio. Additionally, it touches on the aesthetic significance of the golden ratio in human beauty and design.