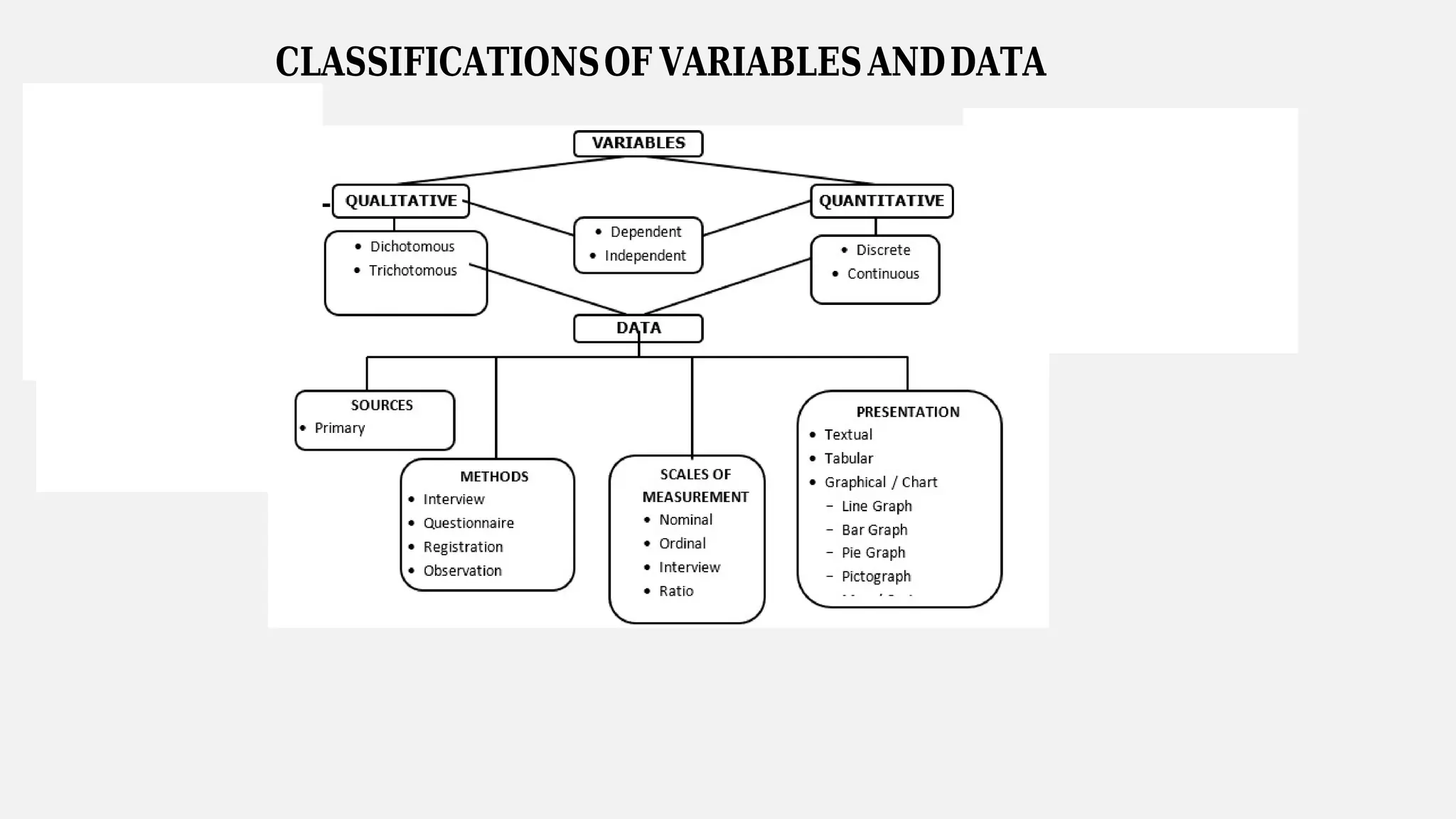
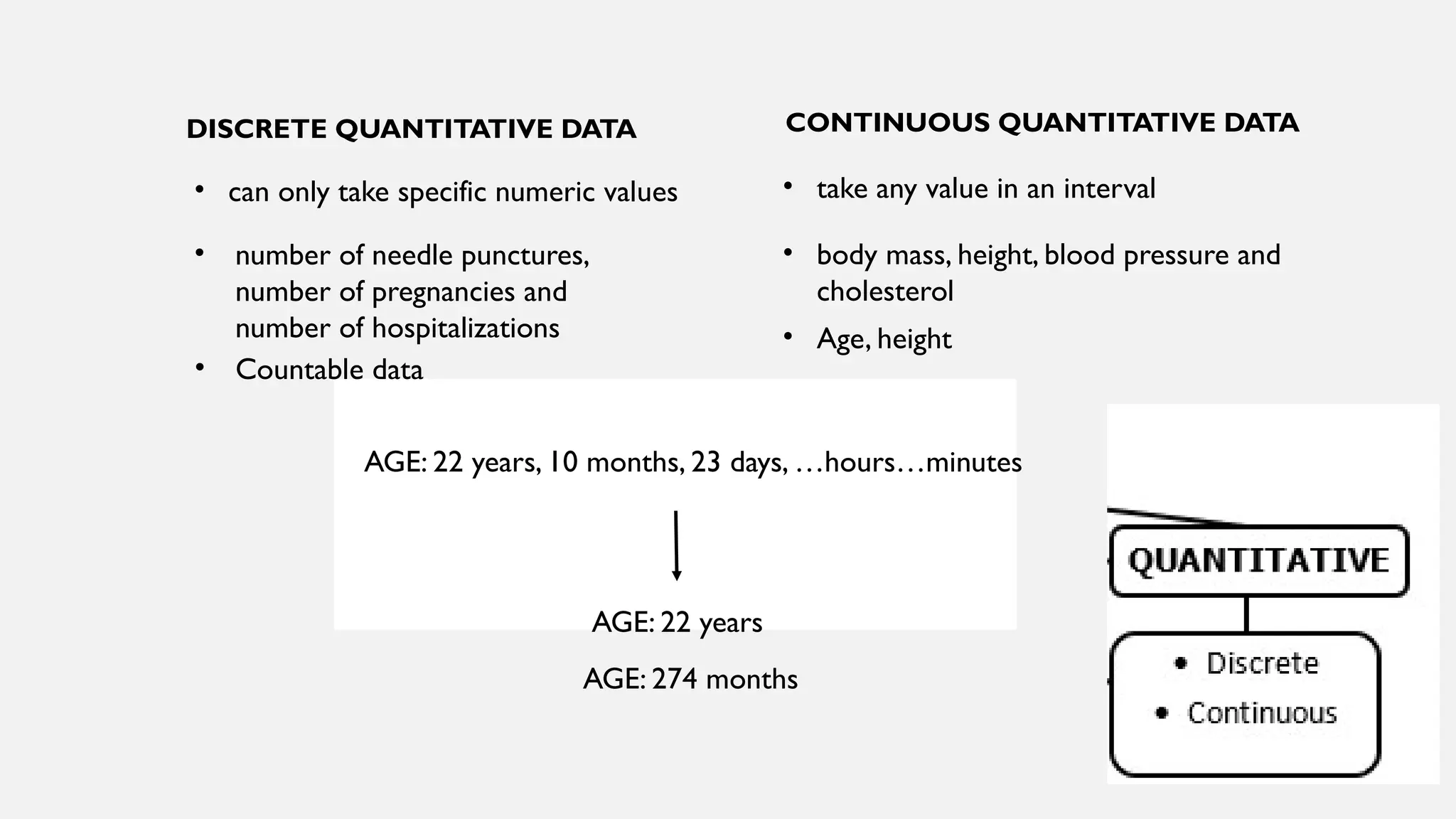
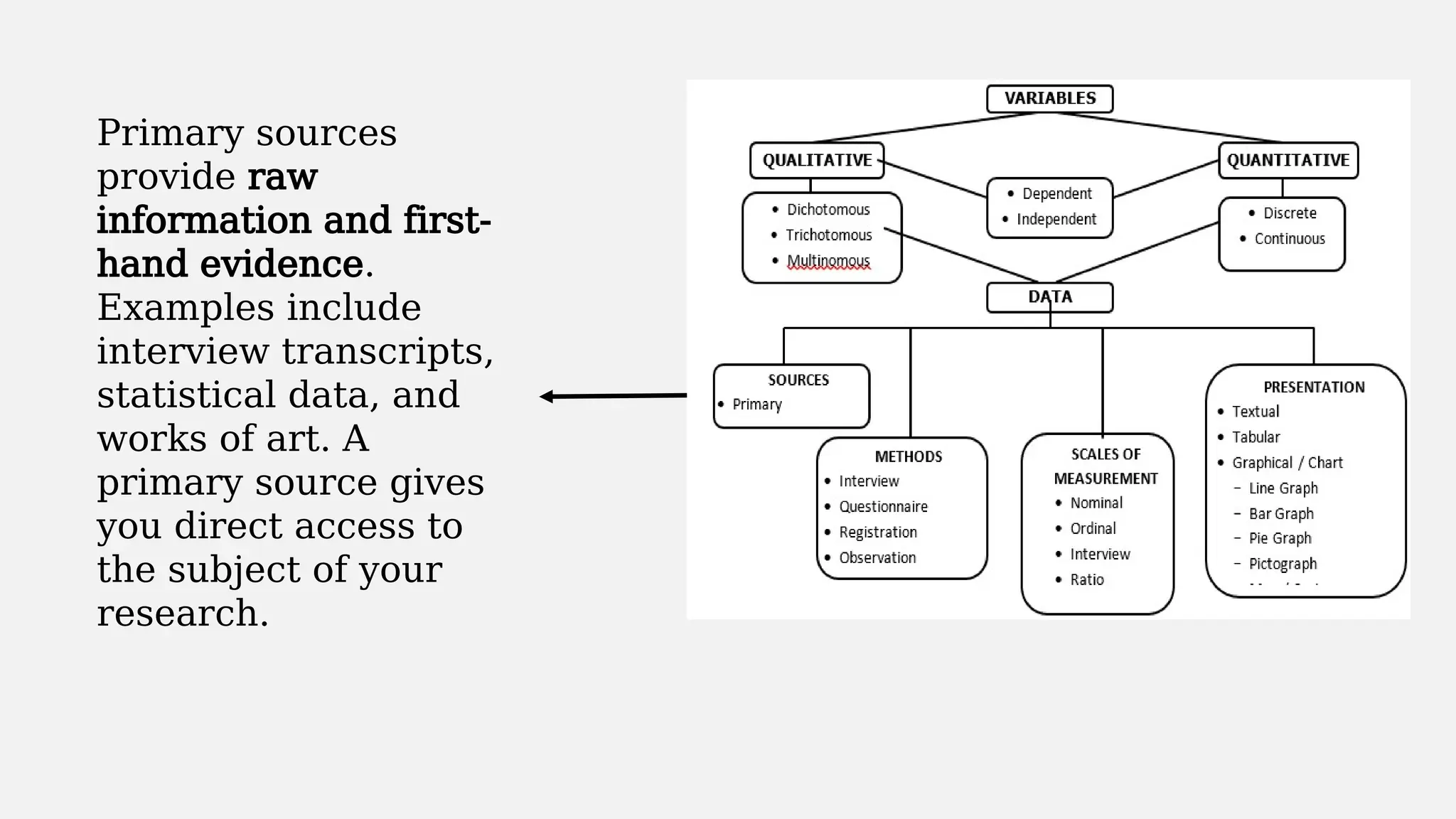
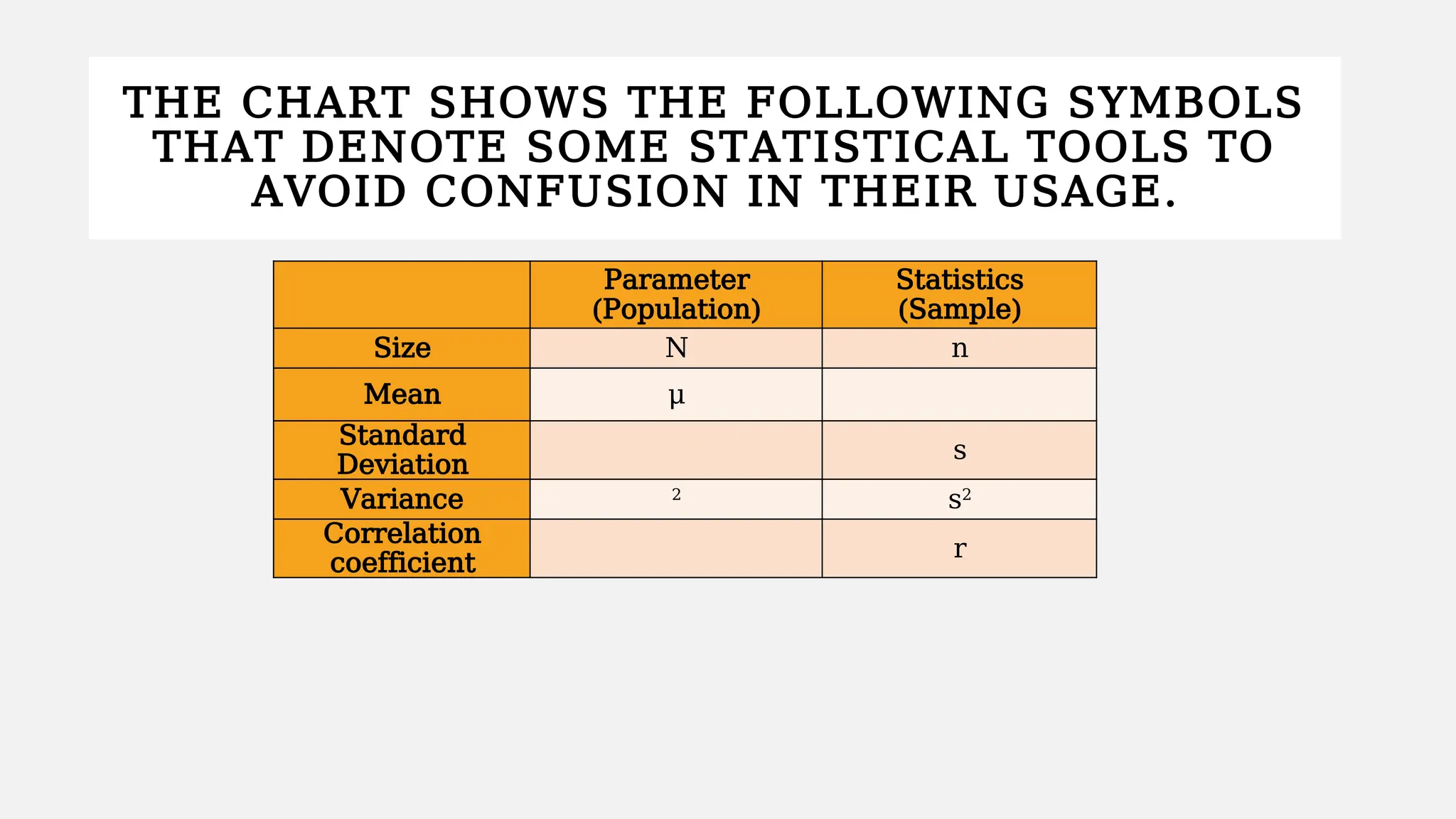
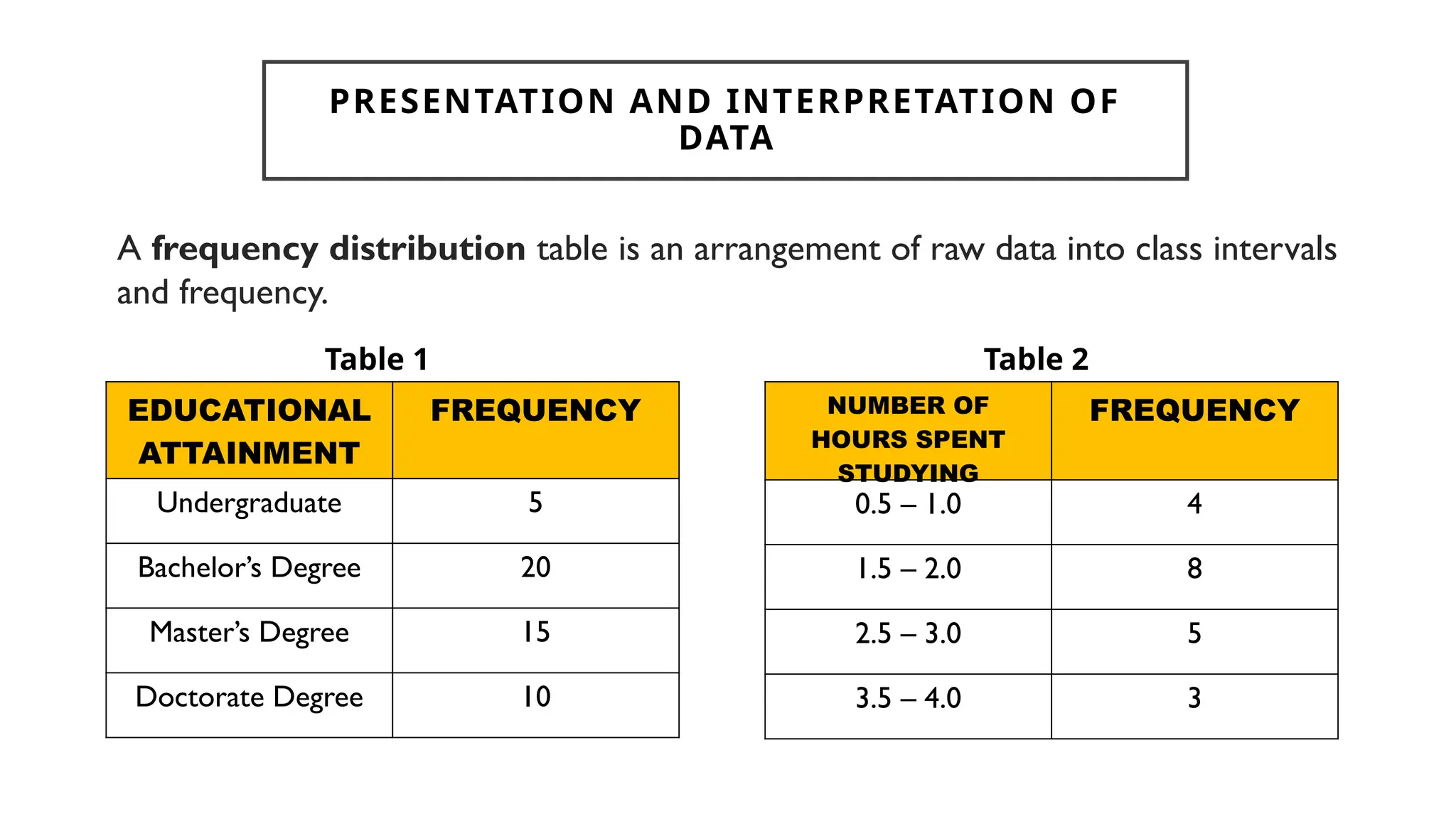
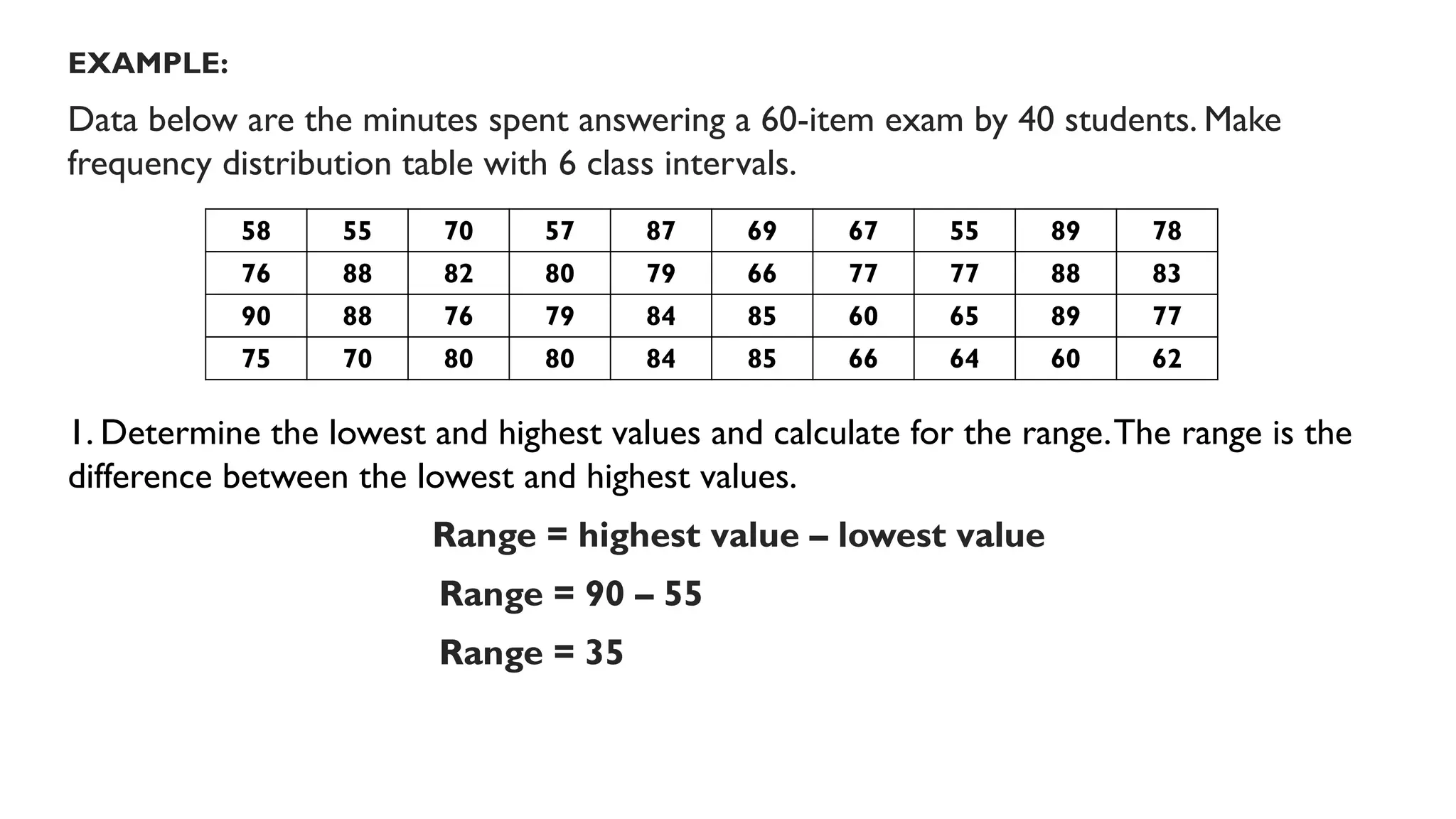
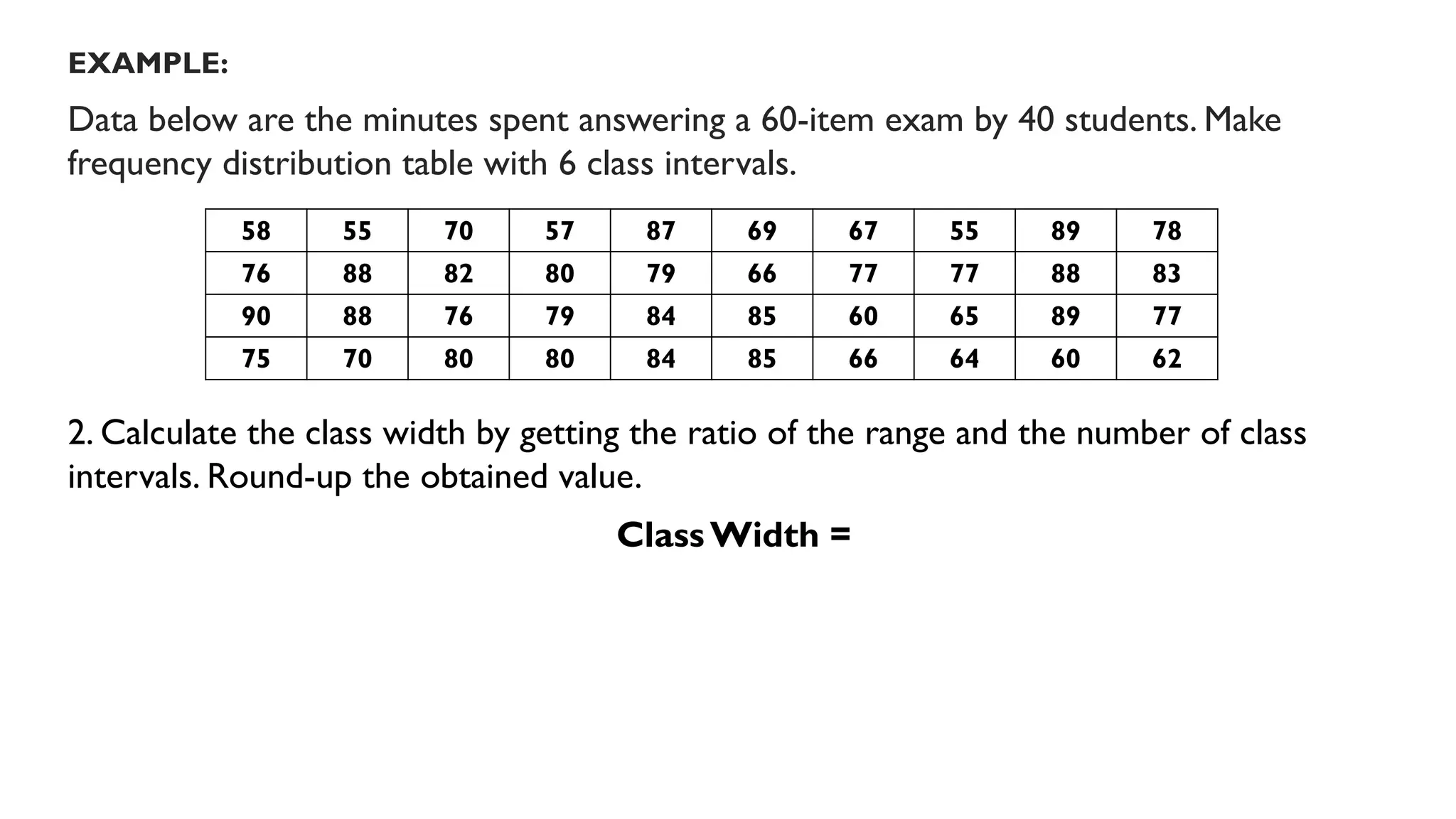
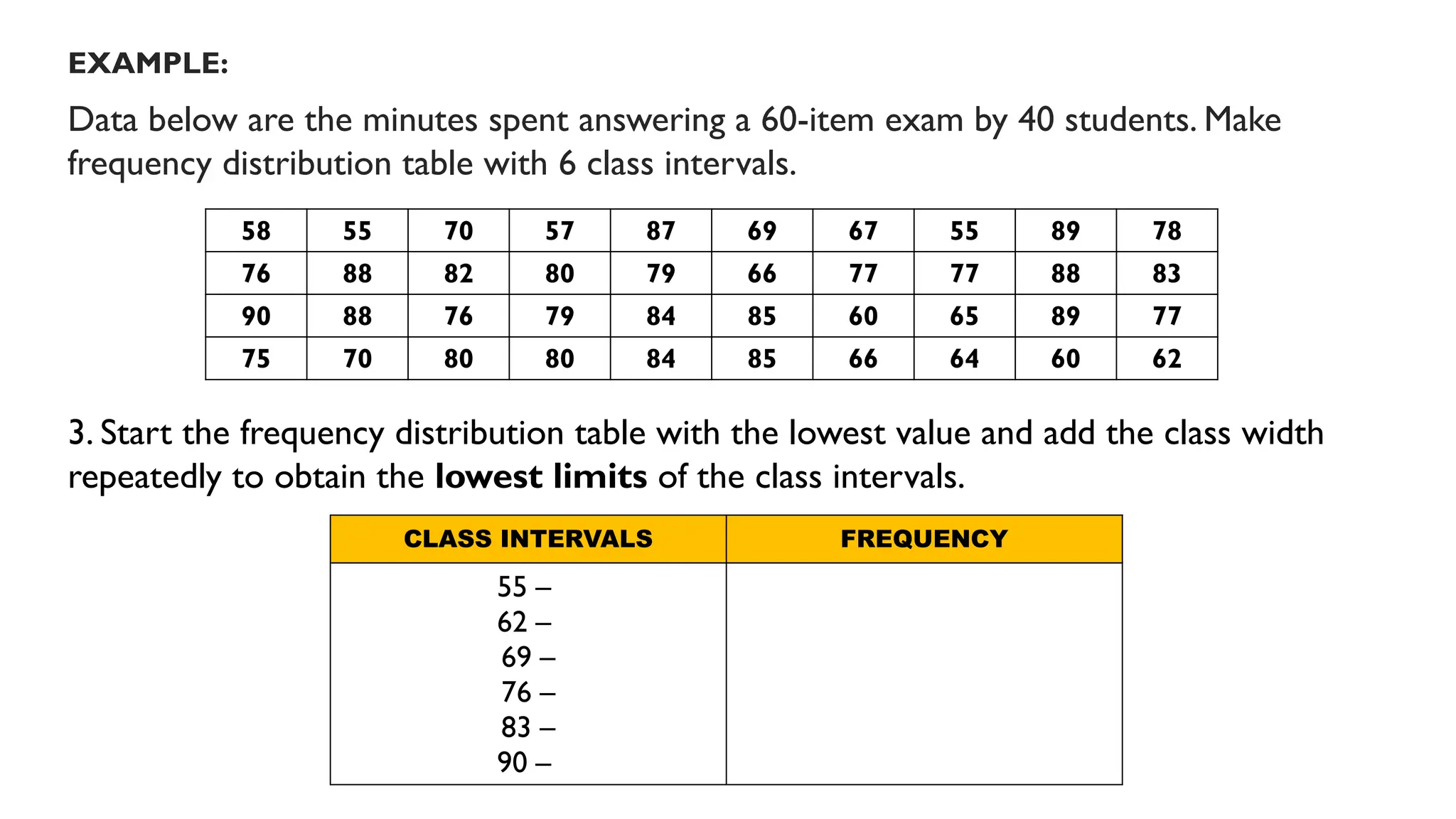
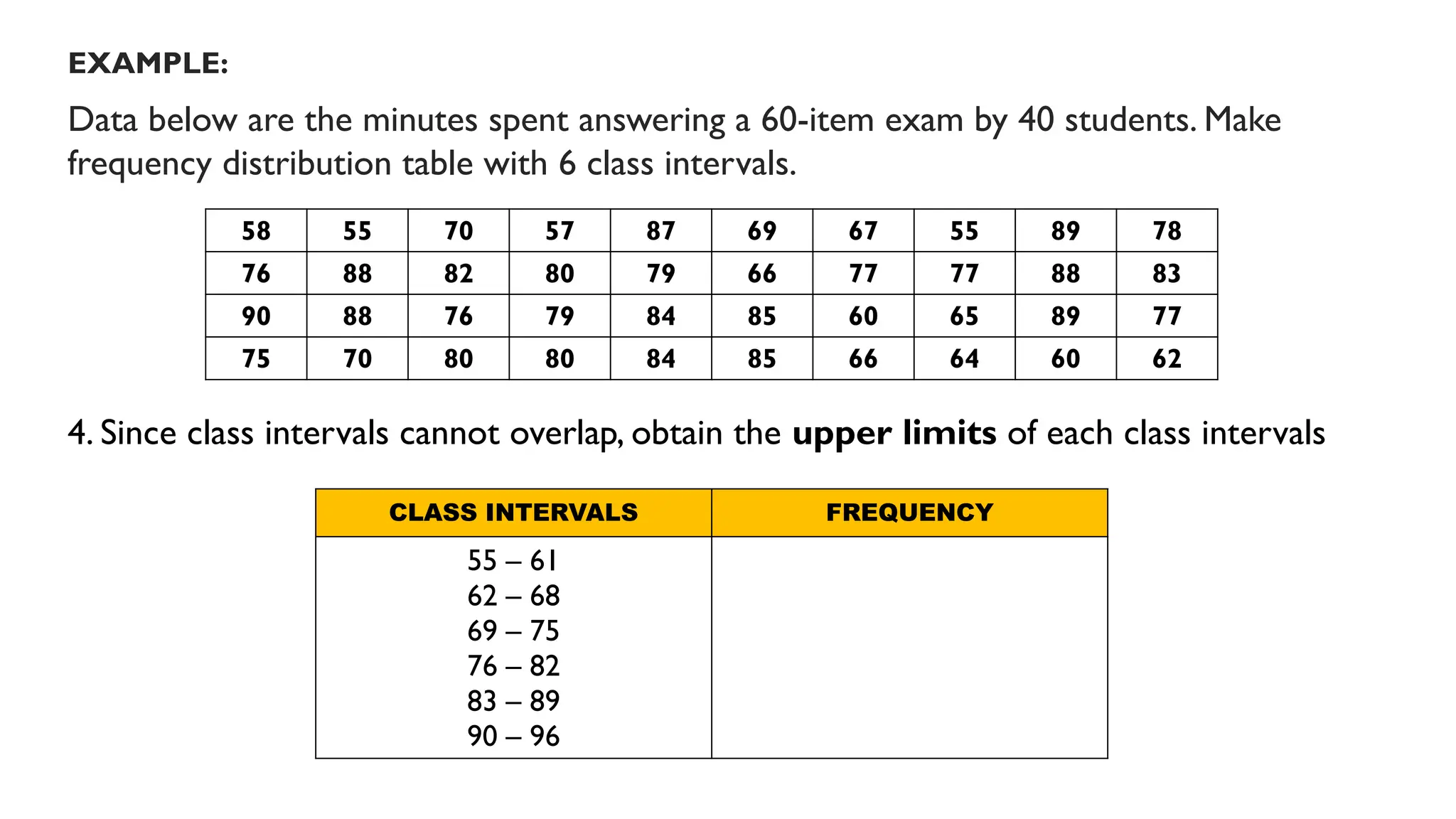
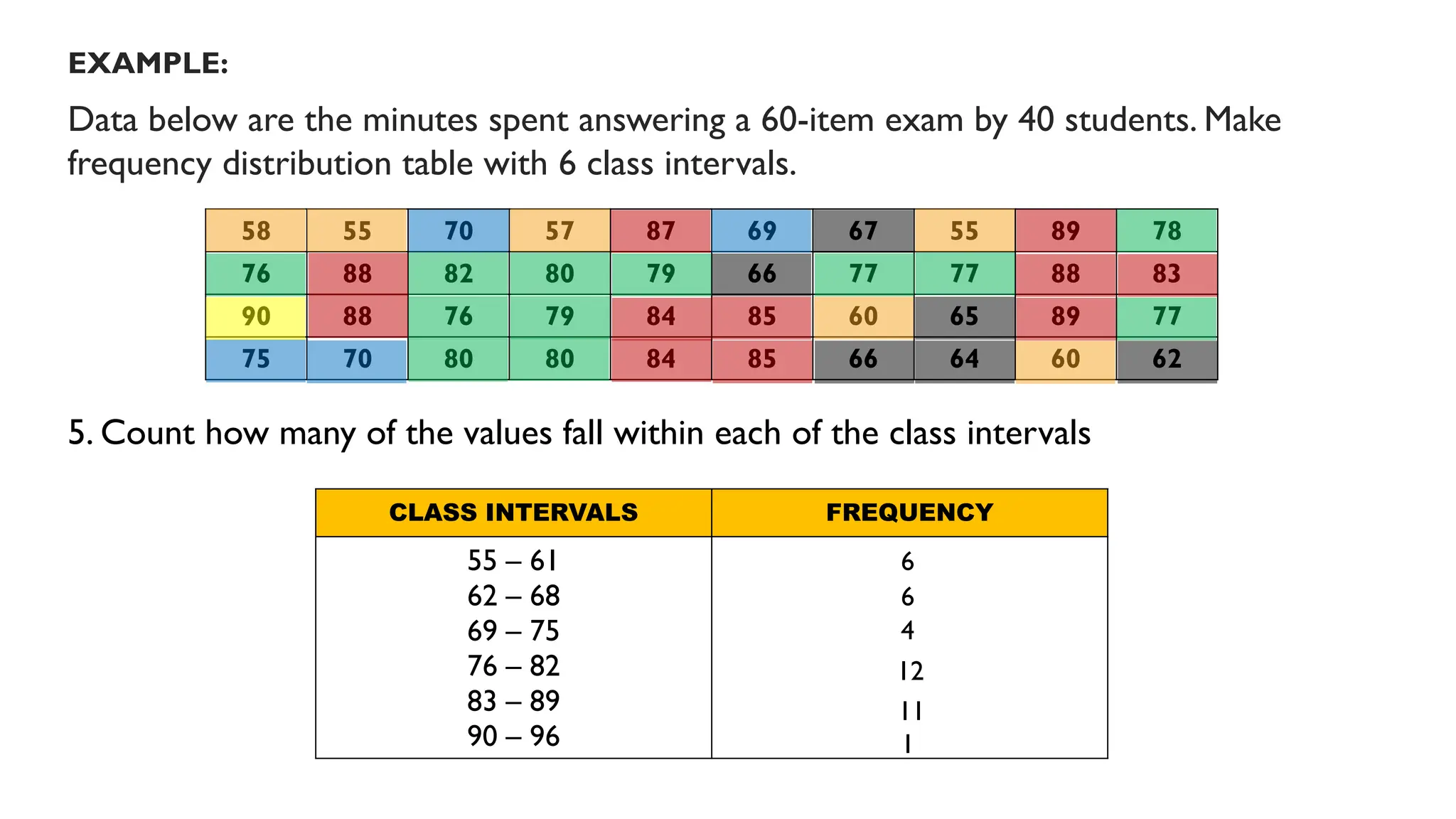
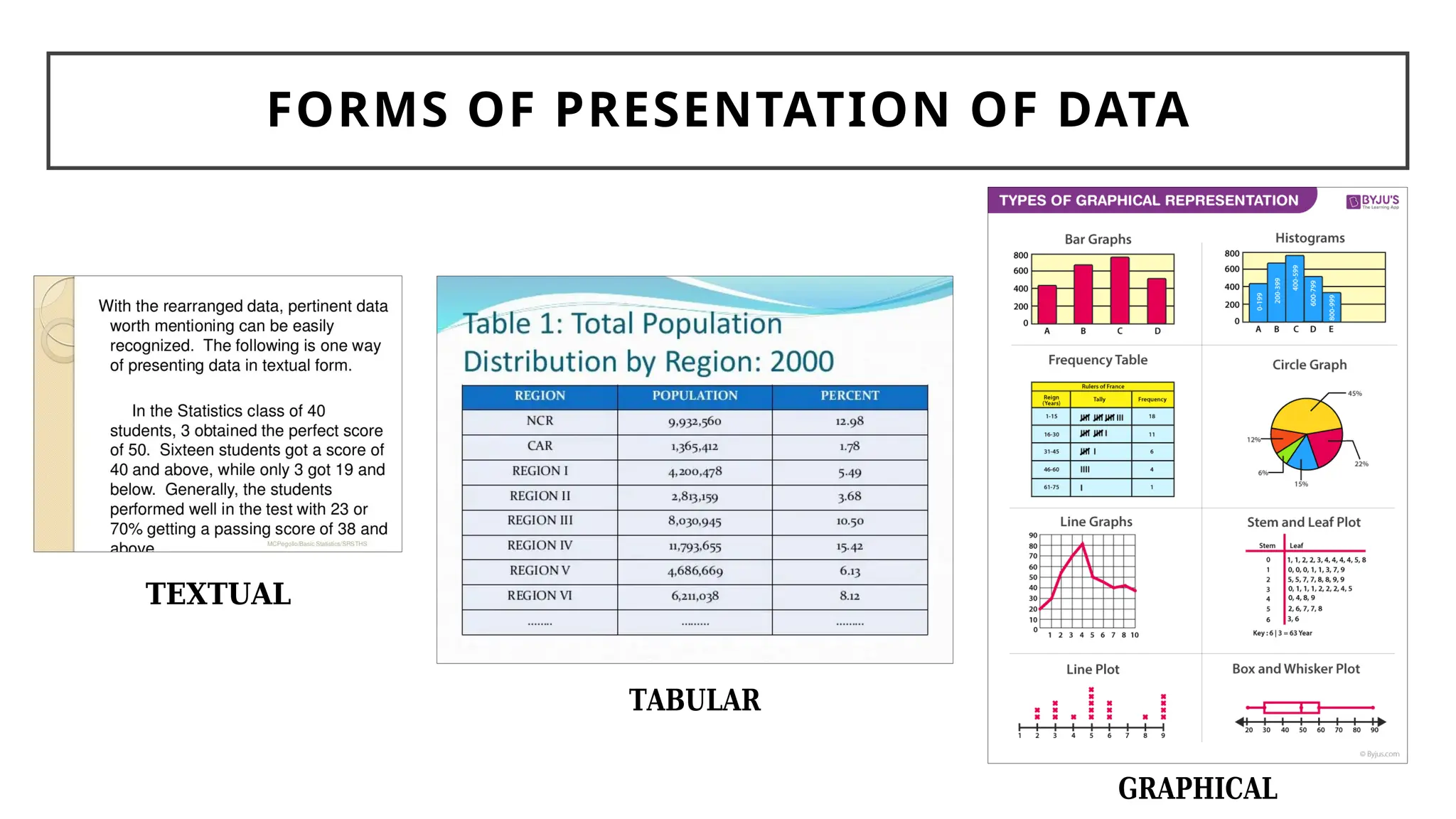
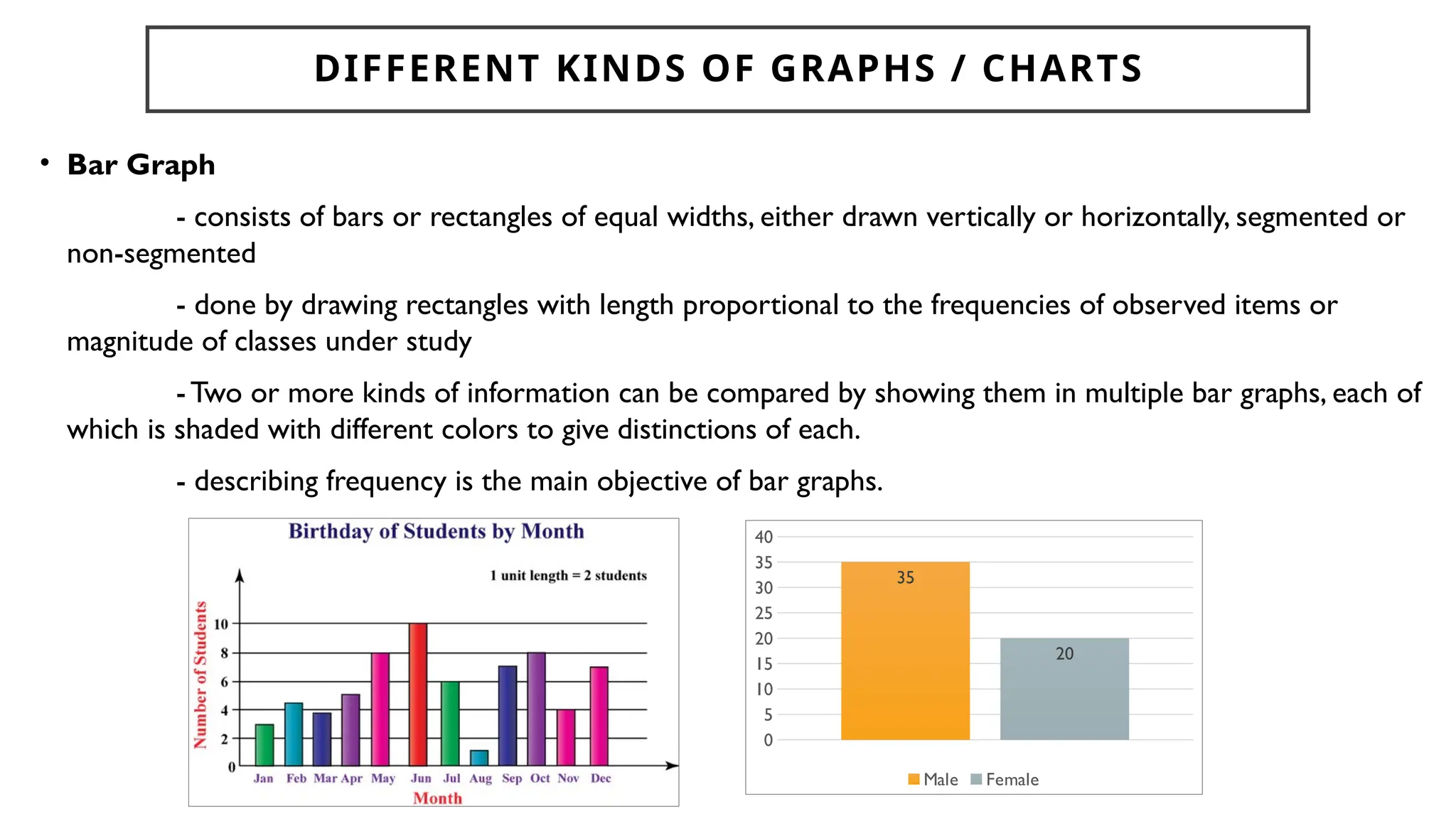
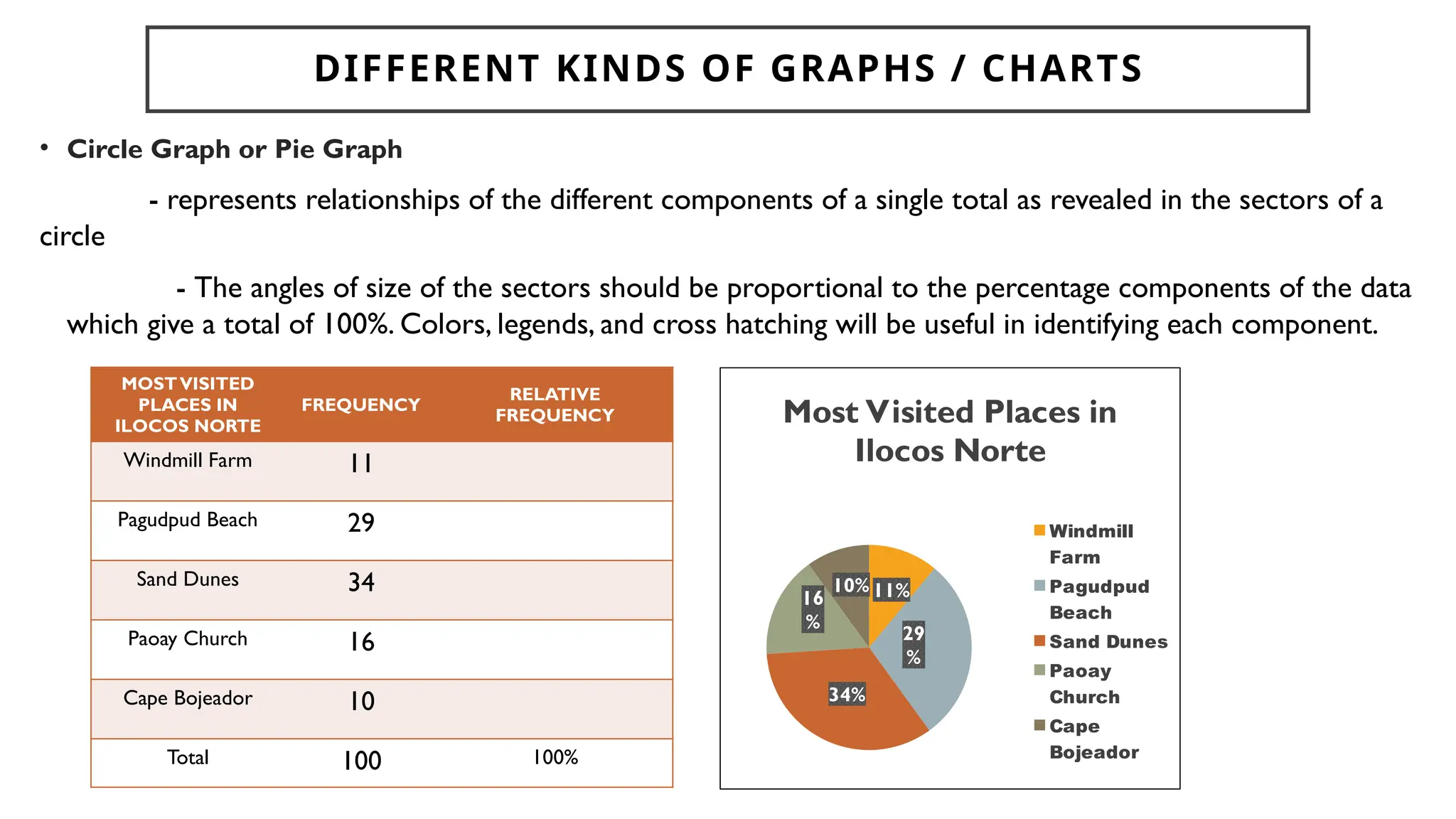
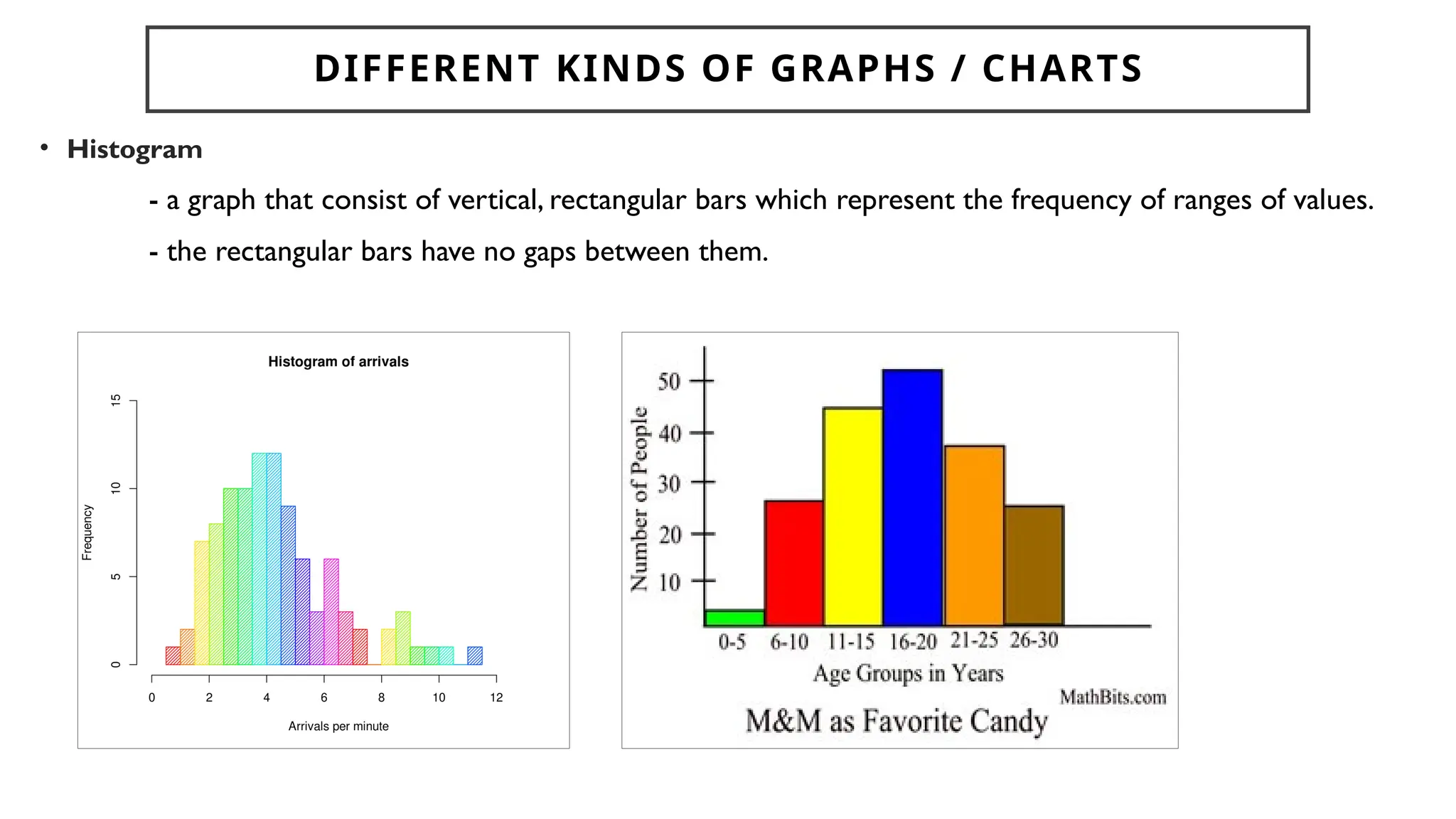
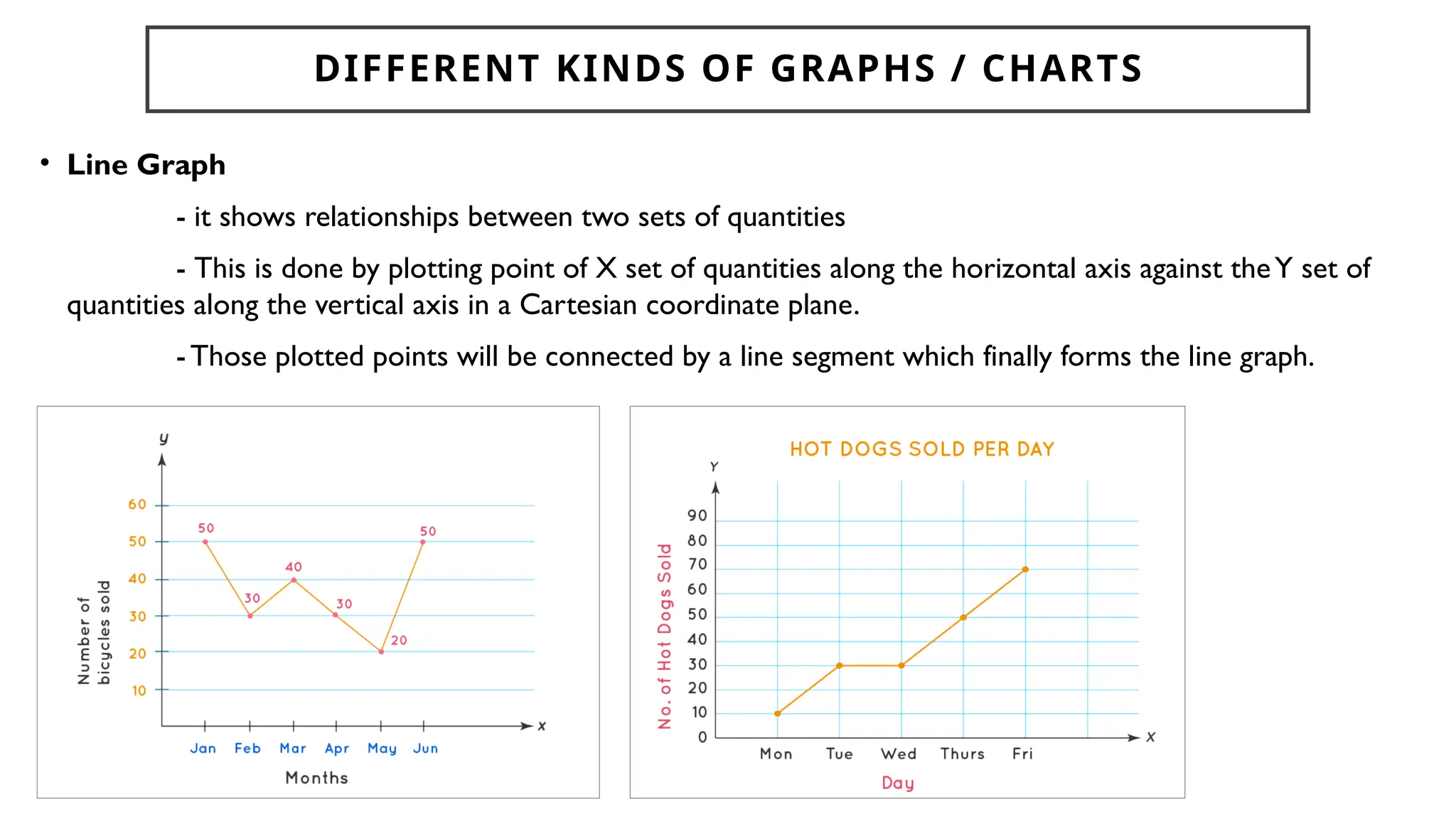
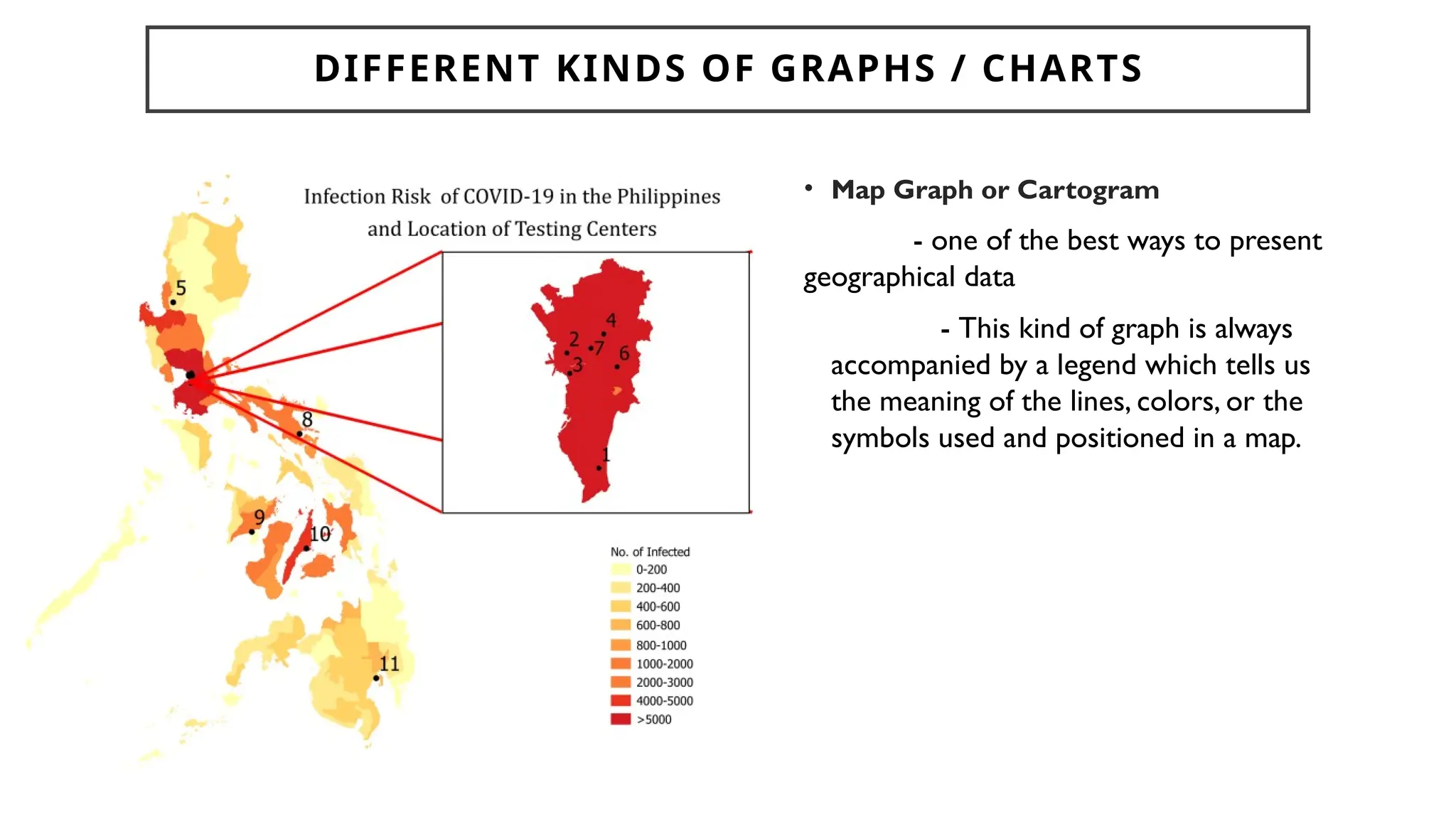
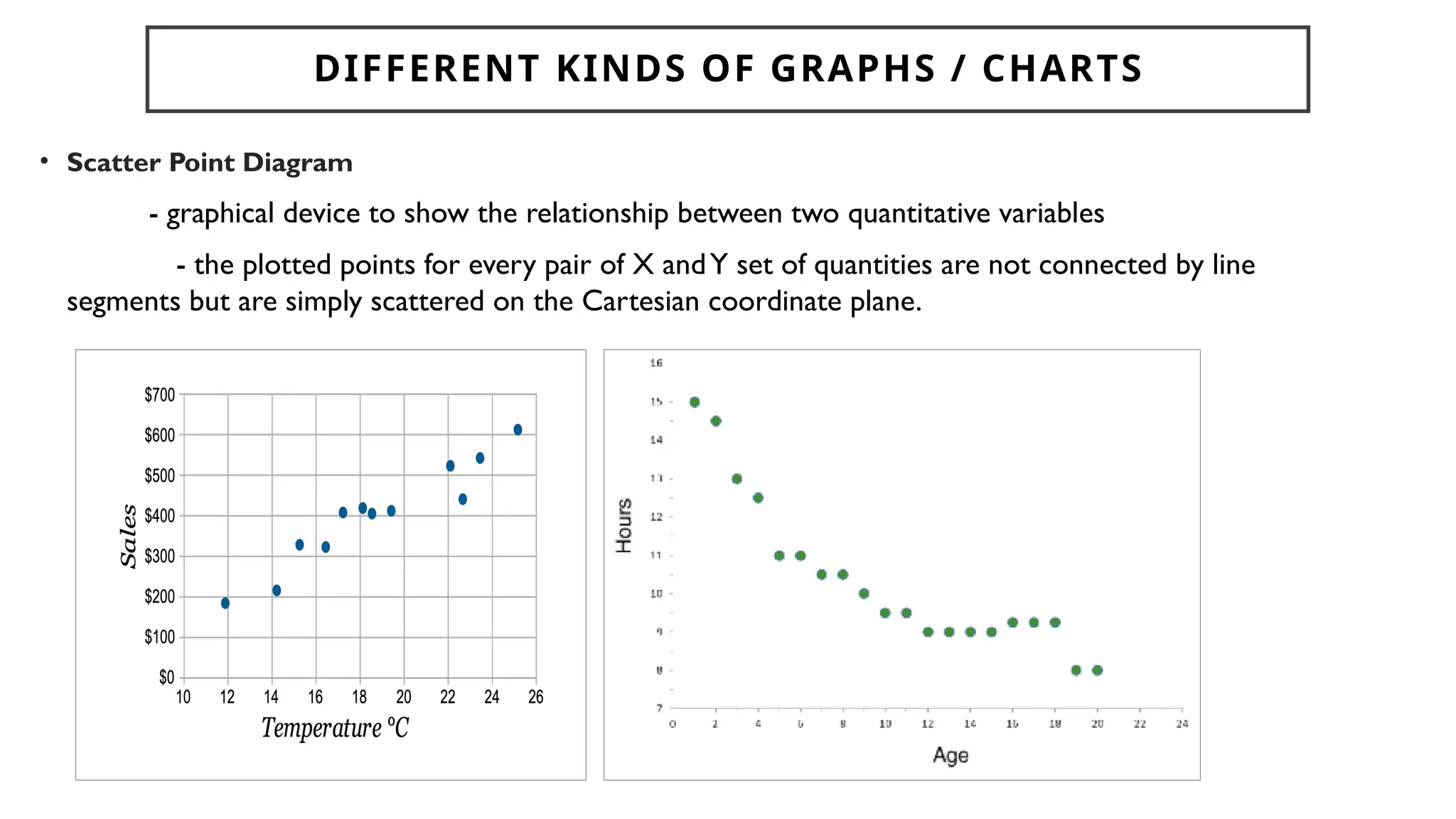
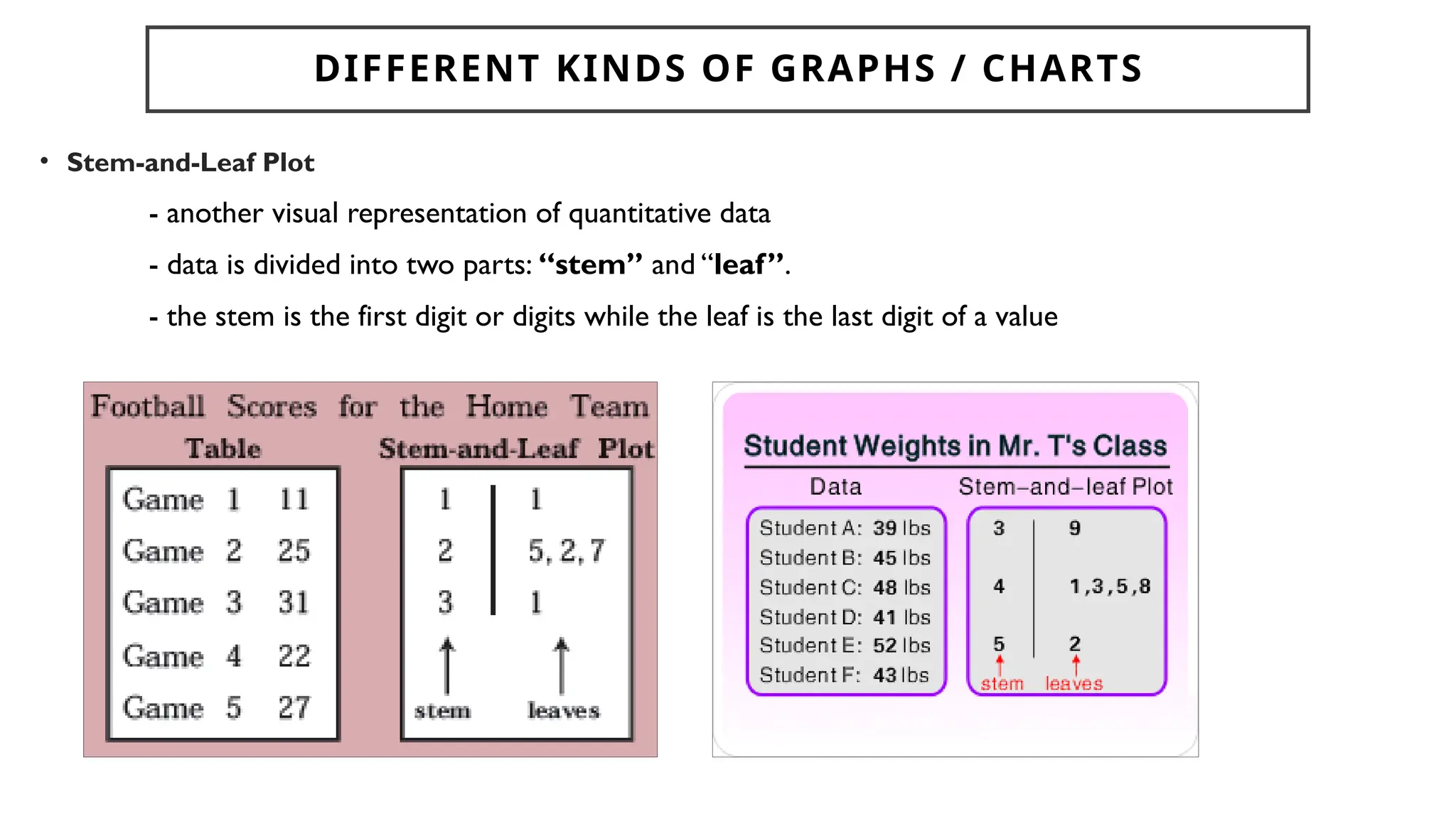
Chapter 4 discusses data formulation and presentation, covering the classification, organization, and interpretation of data, and introduces methods for data collection. It explains the types of variables, the distinction between population and sample, and outlines both random and non-random sampling techniques. Additionally, various forms of data presentation, including textual, tabular, and graphical methods, are highlighted, detailing how to effectively convey statistical information.


![Reference: Learn with Mayora. (2022, January 21). Data collection and presentation | Statistics [Video].YouTube. https://www.youtube.com/watch?v=6N2OA34zNEw](https://image.slidesharecdn.com/week3and4-formulationandpresentationofdata-250209031023-156b97a7/75/WEEK-3-and-4-Formulation-and-Presentation-of-Data-pptx-3-2048.jpg)