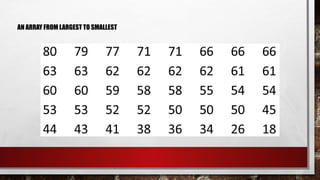
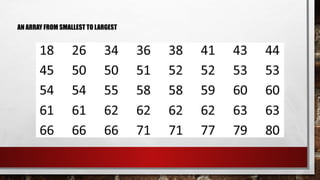
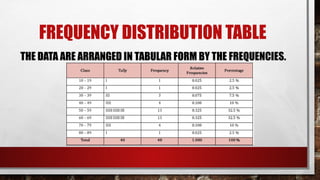
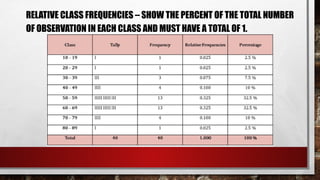
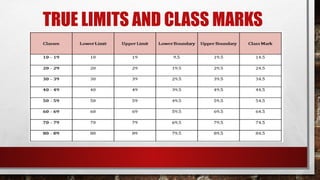
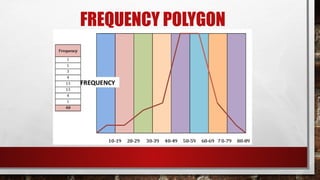
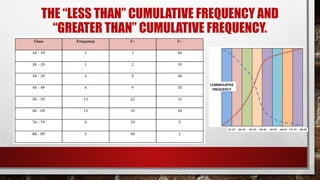
The document discusses the organization of raw data into frequency distribution tables, which group numerical observations into intervals with corresponding counts. It outlines the steps and rules for creating these tables, including class intervals, frequencies, and methods to avoid overlap and ensure equal ranges. Additionally, it introduces concepts such as relative frequency, true limits, class marks, and frequency polygons for visual representation of data.

1. FREQUENCY
DISTRIBUTION TABLE

2. RAW DATA
DATA COLLECTED IN AN INVESTIGATION AND THEY ARE NOT
ORGANIZED SYSTEMATICALLY

3. METHODS OF ORGANIZING THE RAW DATA
ARRAY – ORDERING THE OBSERVATIONS FROM SMALLEST TO
THE LARGEST OR VICE VERSA. IT HAS ADVANTAGES BECAUSE THE
LOW AND HIGH VALUES CAN BE READILY PERCEIVED. THE
PROCESS IS TEDIOUS ESPECIALLY IF THE RAW DATA ARE
NUMEROUS.

4. EXAMPLE : A NATIONWIDE TRAVEL AGENCY OFFERS SPECIAL RATES FOR
PACKAGE TOURS DURING SUMMER. TO ECONOMIZE SPENDING FOR THE
ADVERTISEMENT ONLY CERTAIN AGE GROUP OF PEOPLE WILL BE SENT
BROCHURES FOR ATTRACTION. THE AGENCY GETS TO PREVIOUS PASSENGER
CUSTOMERS FROM ITS FILES AND GROUPS THEM ACCORDING TO AGES.
ONLY THOSE AGE GROUPS WITH LEAST PEOPLE ARE SENT BROCHURES.

5. THE FOLLOWING ARE THE AGES OF THE PREVIOUS CUSTOMERS:

6. AN ARRAY FROM LARGEST TO SMALLEST

7. AN ARRAY FROM SMALLEST TO LARGEST

8. FREQUENCY DISTRIBUTION TABLE
•IT IS THE GROUPING OF ALL THE (NUMERICAL) OBSERVATION INTO INTERVALS
OR CLASSES TOGETHER WITH A COUNT OF THE NUMBER OF OBSERVATIONS
THAT FALL IN EACH INTERVAL OR CLASS.
•IT IS AN ORDERLY ARRANGEMENT OF DATA CLASSIFIED ACCORDING TO THE
SIZE OF THE OBSERVATION.
•WE CONSTRUCT FREQUENCY DISTRIBUTION TABLE (FDT) IF THERE ARE
ATLEAST 30 DATA OBSERVATION OR RAW SCORES.

9. FREQUENCY - THE NUMBER OF TIMES A VALUE APPEARS IN
THE LISTING OR COLLECTED DATA.
RELATIVE FREQUENCY - ANY OBSERVATION IS OBTAINED BY
DIVIDING THE ACTUAL FREQUENCY OF THE OBSERVATION BY
THE TOTAL FREQUENCY.

10. FREQUENCY DISTRIBUTION TABLE
THE DATA ARE ARRANGED IN TABULAR FORM BY THE FREQUENCIES.

11. STEPS IN THE CONTRUCTION OF FREQUENCY
DISTRIBUTION TABLE
1. DECIDING ON THE SET OF GROUPINGS CALLED CLASSES,
2.SORTING OR TALLYING THE DATA INTO CLASSES AND
3.COUNTING THE NUMBER OF TALLIES IN EACH CLASS CALLED
CLASS FREQUENCIES

12. RULES IN CONSTRUCTING FDT
1. WE SELDOM USE FEWER THAN 5 OR MORE THAN 15 CLASSES.
2. THE CLASSES COVER EQUAL RANGES OF VALUES AND MAKE RANGES
MULTIPLES OF NUMBERS THAT ARE EASY TO WORK WITH. OPEN CLASSES
SHOULD BE AVOIDED SUCH AS CLASSES OF “LESS THAN” OR “MORE THAN”.
3. CLASSES SHOULD NOT OVERLAP
4. IN THE FINAL PRESENTATION OF THE TABLE, TALLY IS USUALLY OMITTED.

13. •CLASS INTERVAL REFERS TO THE NUMERICAL WIDTH OF ANY
CLASS IN A PARTICULAR DISTRIBUTION. IT IS DEFINED AS THE
DIFFERENCE BETWEEN THE UPPER-CLASS LIMIT AND THE LOWER
CLASS LIMIT. CLASS INTERVAL = UPPER-CLASS LIMIT – LOWER
CLASS LIMIT.
•THE CLASS SIZE IS THE DIFFERENCE BETWEEN THE LOWER AND
UPPER CLASS-LIMITS.

14. THE VALUE OF IS CALLED STURGE’S RULE, WHERE K IS THE
NUMBER OF CLASSES, AND N IS THE SAMPLE SIZE TO GET
THE DESIRED CLASS SIZE.
ANOTHER WAY IS BY USING RULE, WHERE N IS THE SAMPLE
SIZE. THEREFORE,

15. FREUD AND SIMON SUGGESTED THE FORMULA IN DECIDING THE
CLASS INTERVAL.
A CONVENIENT VALUE TO START THE FIRST CLASS IS THE SMALLEST VALUE OF THE ARRAY OF NUMBERS.

16. RELATIVE CLASS FREQUENCIES – SHOW THE PERCENT OF THE TOTAL NUMBER
OF OBSERVATION IN EACH CLASS AND MUST HAVE A TOTAL OF 1.

17. TRUE LIMITS AND CLASS MARKS
•A POINT THAT REPRESENTS THE HALFWAY POINT BETWEEN SUCCESSIVE
CLASSES IS CALLED A TRUE LIMIT OR CLASS BOUNDARY. IT IS OBTAINED BY
ADDING THE UPPER LIMIT OF ONE CLASS AND THE LOWER LIMIT OF THE NEXT
CLASS THEN DIVING BY 2.
•A POINT THAT REPRESENTS THE HALFWAY BETWEEN THE LOWER LIMIT AND
THE UPPER LIMIT IS CALLED THE CLASS MARK. IT IS OBTAINED BY ADDING THE
LOWER LIMIT AND UPPER LIMIT OF THE SAME CLASS AND THEN DIVIDING BY 2.

18. TRUE LIMITS AND CLASS MARKS

19. FREQUENCY POLYGON

20. OGIVE
•A LINE GRAPH REPRESENTING THE UPPER CLASS BOUNDARIES
ALONG THE HORIZONTAL AXIS AND THE CORRESPONDING
CUMULATIVE FREQUENCIES ALONG THE VERTICAL AXIS. IT IS
ALSO CALLED “LESS THAN” CUMULATIVE FREQUENCY POLYGON;
OTHERWISE IT IS THE “GREATER THAN” CUMULATIVE FREQUENCY
POLYGON.

21. THE “LESS THAN” CUMULATIVE FREQUENCY AND
“GREATER THAN” CUMULATIVE FREQUENCY.