Fundamental Theorem Calculus Notes

Section 5.4
The Fundamental Theorem of Calculus

V63.0121.006/016, Calculus I

New York University

April 22, 2010

Announcements

April 29: Movie Day
April 30: Quiz 5 on §§5.1–5.4
Monday, May 10, 12:00noon Final Exam

. . . . . . .

Announcements

April 29: Movie Day
April 30: Quiz 5 on
§§5.1–5.4
Monday, May 10,
12:00noon Final Exam

. . . . . .

V63.0121.006/016, Calculus I (NYU) Section 5.4 The Fundamental Theorem April 22, 2010 2 / 34

Resurrection policies

Current distribution of grade: 40% final, 25% midterm, 15%
quizzes, 10% written HW, 10% WebAssign
Remember we drop the lowest quiz, lowest written HW, and
5 lowest WebAssign-ments
If your final exam score beats your midterm score, we will
re-weight it by 50% and make the midterm 15%

. . . . . .


Objectives

State and explain the
Fundemental Theorems of
Calculus
Use the first fundamental
theorem of calculus to find
derivatives of functions
defined as integrals.
Compute the average
value of an integrable
function over a closed
interval.

. . . . . .


Outline

Recall: The Evaluation Theorem a/k/a 2FTC

The First Fundamental Theorem of Calculus
The Area Function
Statement and proof of 1FTC
Biographies

Differentiation of functions defined by integrals
“Contrived” examples
Erf
Other applications

. . . . . .


The definite integral as a limit

Definition
If f is a function defined on [a, b], the definite integral of f from a to b
is the number ∫ b ∑n
f(x) dx = lim f(ci ) ∆x
a ∆x→0
i=1

. . . . . .


Theorem (The Second Fundamental Theorem of Calculus)
Suppose f is integrable on [a, b] and f = F′ for another function F, then
∫ b
f(x) dx = F(b) − F(a).
a

. . . . . .


The Integral as Total Change

Another way to state this theorem is:
∫ b
F′ (x) dx = F(b) − F(a),
a

or the integral of a derivative along an interval is the total change
between the sides of that interval. This has many ramifications:

. . . . . .



∫ b
F′ (x) dx = F(b) − F(a),
a


Theorem
If v(t) represents the velocity of a particle moving rectilinearly, then
∫ t1
v(t) dt = s(t1 ) − s(t0 ).
t0

. . . . . .



∫ b
F′ (x) dx = F(b) − F(a),
a


Theorem
If MC(x) represents the marginal cost of making x units of a product,
then ∫ x
C(x) = C(0) + MC(q) dq.
0

. . . . . .



∫ b
F′ (x) dx = F(b) − F(a),
a


Theorem
If ρ(x) represents the density of a thin rod at a distance of x from its
end, then the mass of the rod up to x is
∫ x
m(x) = ρ(s) ds.
0
. . . . . .


My first table of integrals
.

∫ ∫ ∫
[f(x) + g(x)] dx = f(x) dx + g(x) dx
∫ ∫ ∫
xn+1
xn dx = + C (n ̸= −1) cf(x) dx = c f(x) dx
n+1 ∫
∫
1
ex dx = ex + C dx = ln |x| + C
x
∫ ∫
ax
sin x dx = − cos x + C ax dx = +C
ln a
∫ ∫
cos x dx = sin x + C csc2 x dx = − cot x + C
∫ ∫
2
sec x dx = tan x + C csc x cot x dx = − csc x + C
∫ ∫
1
sec x tan x dx = sec x + C √ dx = arcsin x + C
∫ 1 − x2
1
dx = arctan x + C
1 + x2
. . . . . . .


Outline


The Area Function
Biographies

Erf
Other applications

. . . . . .


An area function
∫ x
Let f(t) = t3 and define g(x) = f(t) dt. Can we evaluate the integral
0
in g(x)?

.
0
. x
.

. . . . . .


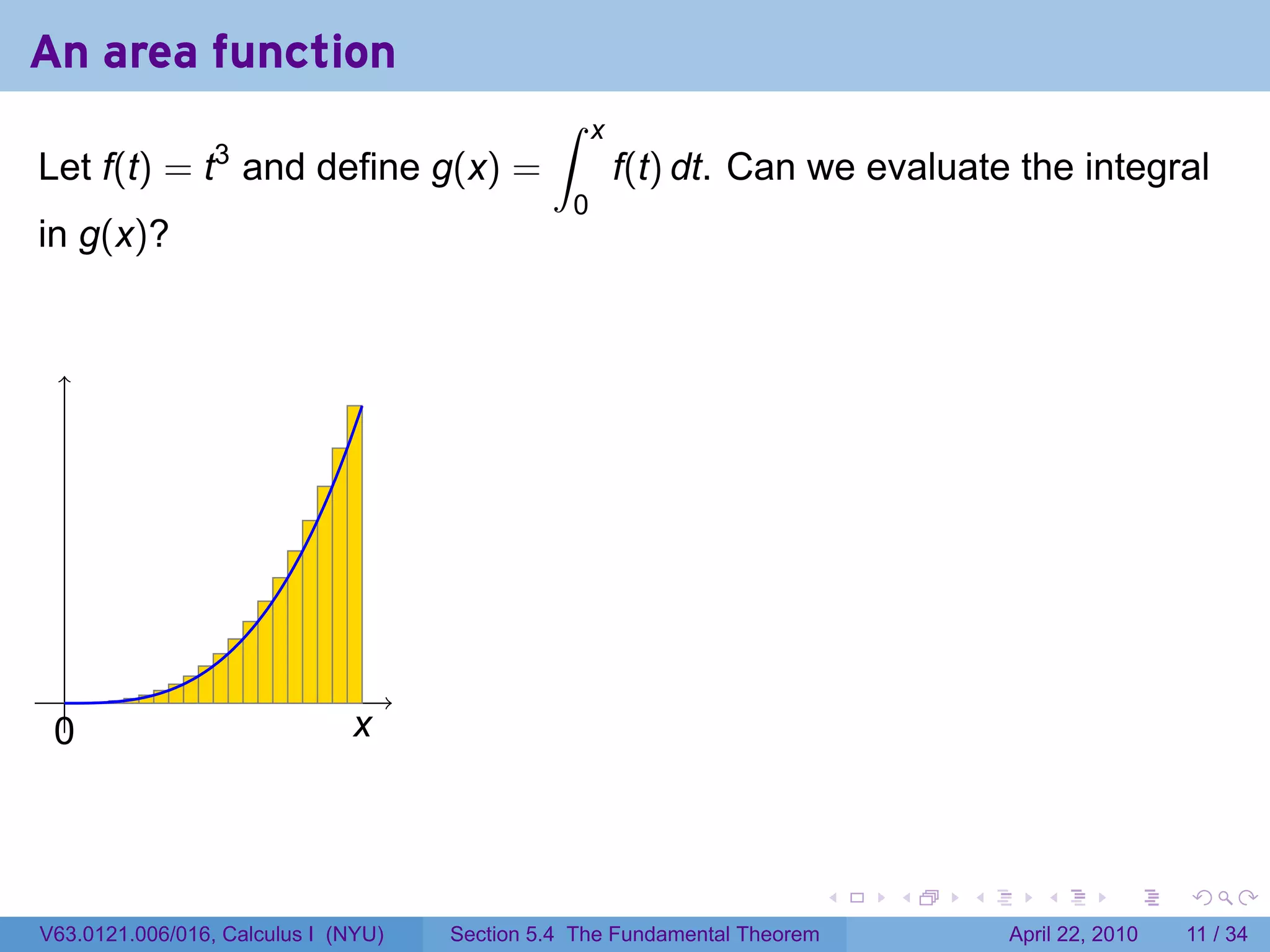
An area function
∫ x
Let f(t) = t3 and define g(x) = f(t) dt. Can we evaluate the integral
0
in g(x)?
Dividing the interval [0, x] into n pieces
x ix
gives ∆t = and ti = 0 + i∆t = . So
n n
x x3 x (2x)3 x (nx)3
Rn = · 3+ · + ··· + ·
n n n n3 n n3
x4 ( )
= 4 13 + 23 + 33 + · · · + n3
n
x4 [ ]2
= 4 1 n(n + 1)
. n 2
0
. x
.
x4 n2 (n + 1)2 x4
= →
4n4 4
as n → ∞.
. . . . . .


An area function, continued

So
x4
g(x) = .
4

. . . . . .


An area function, continued

So
x4
g(x) = .
4
This means that
g′ (x) = x3 .

. . . . . .


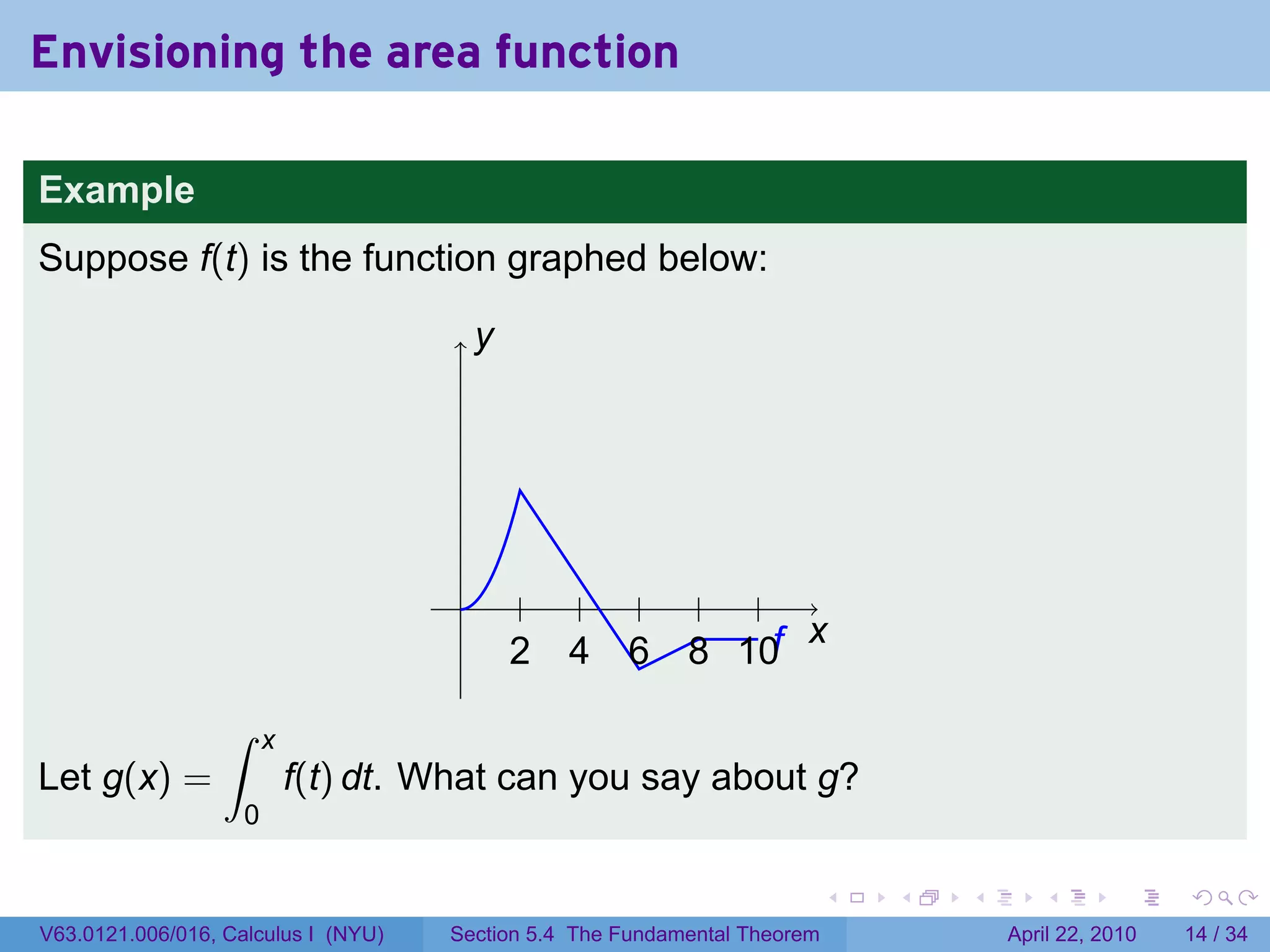
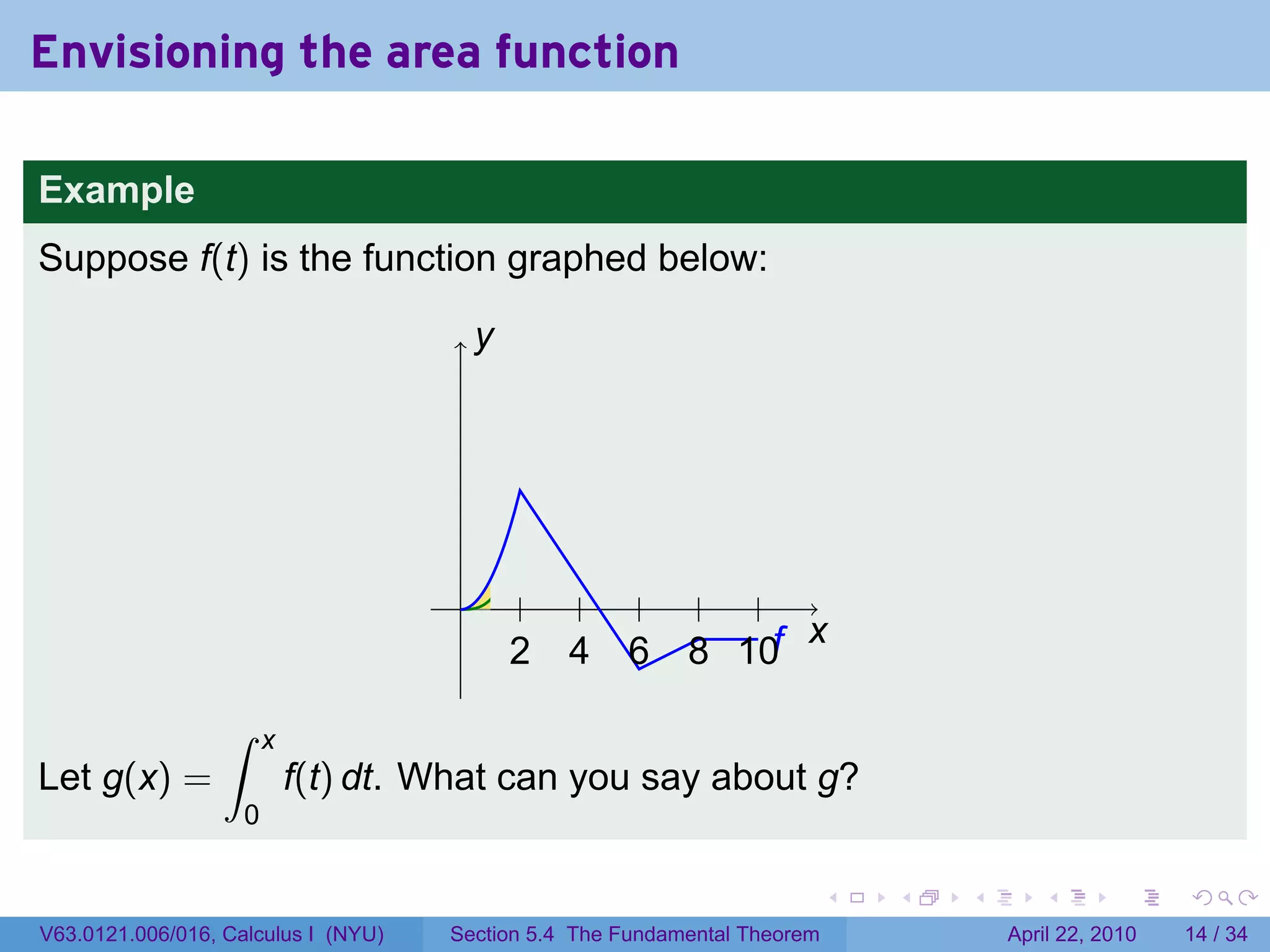
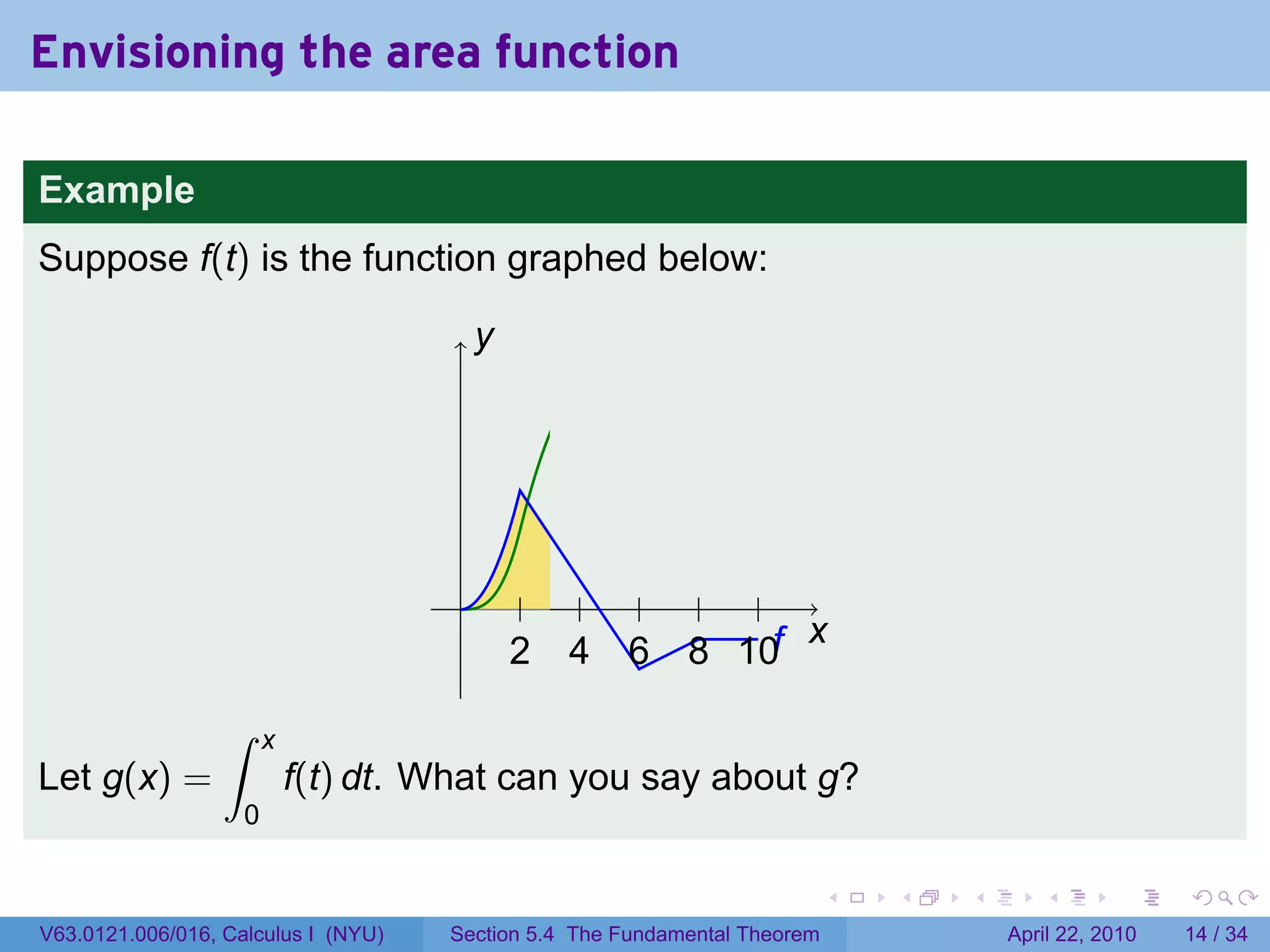
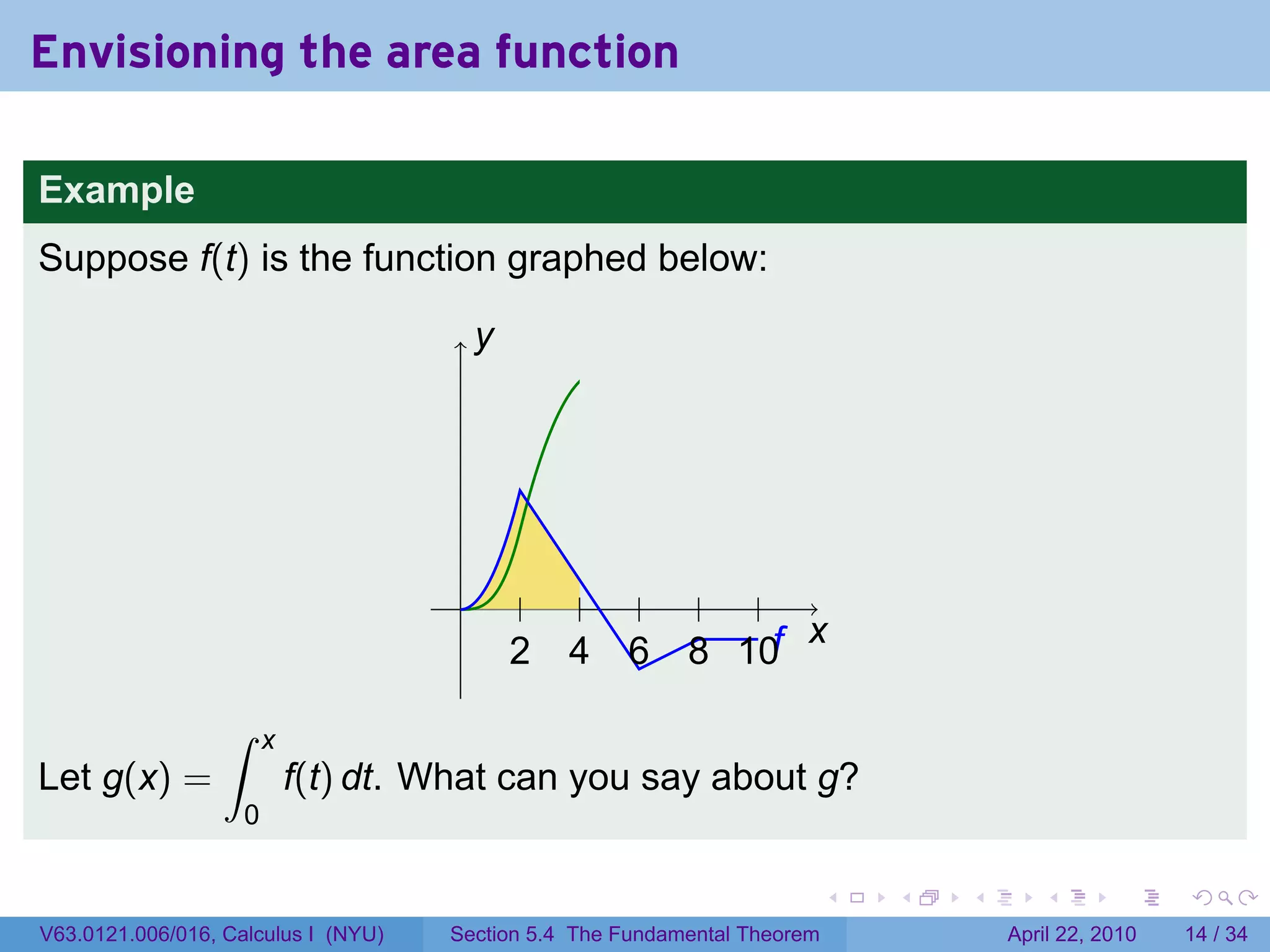
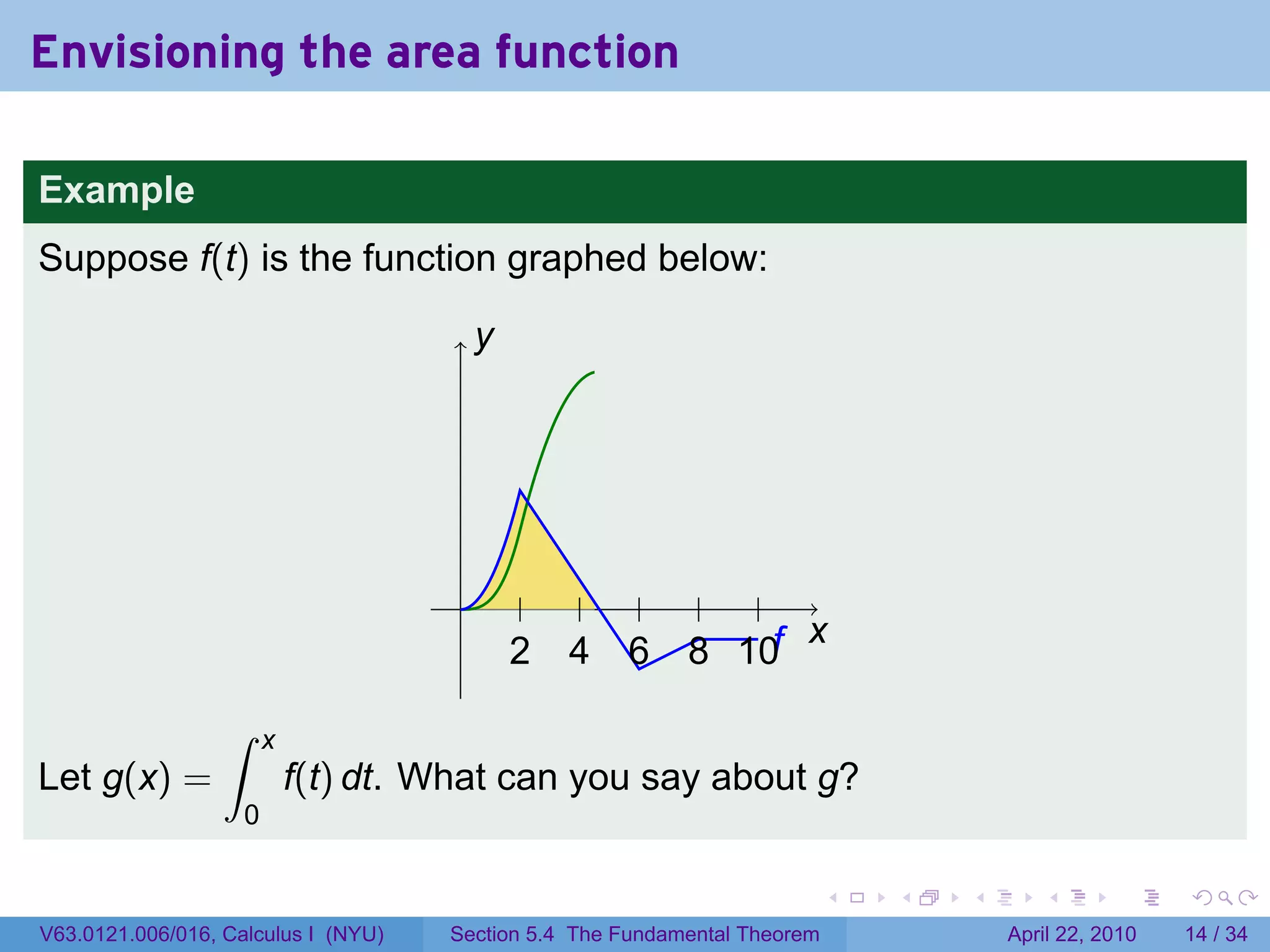
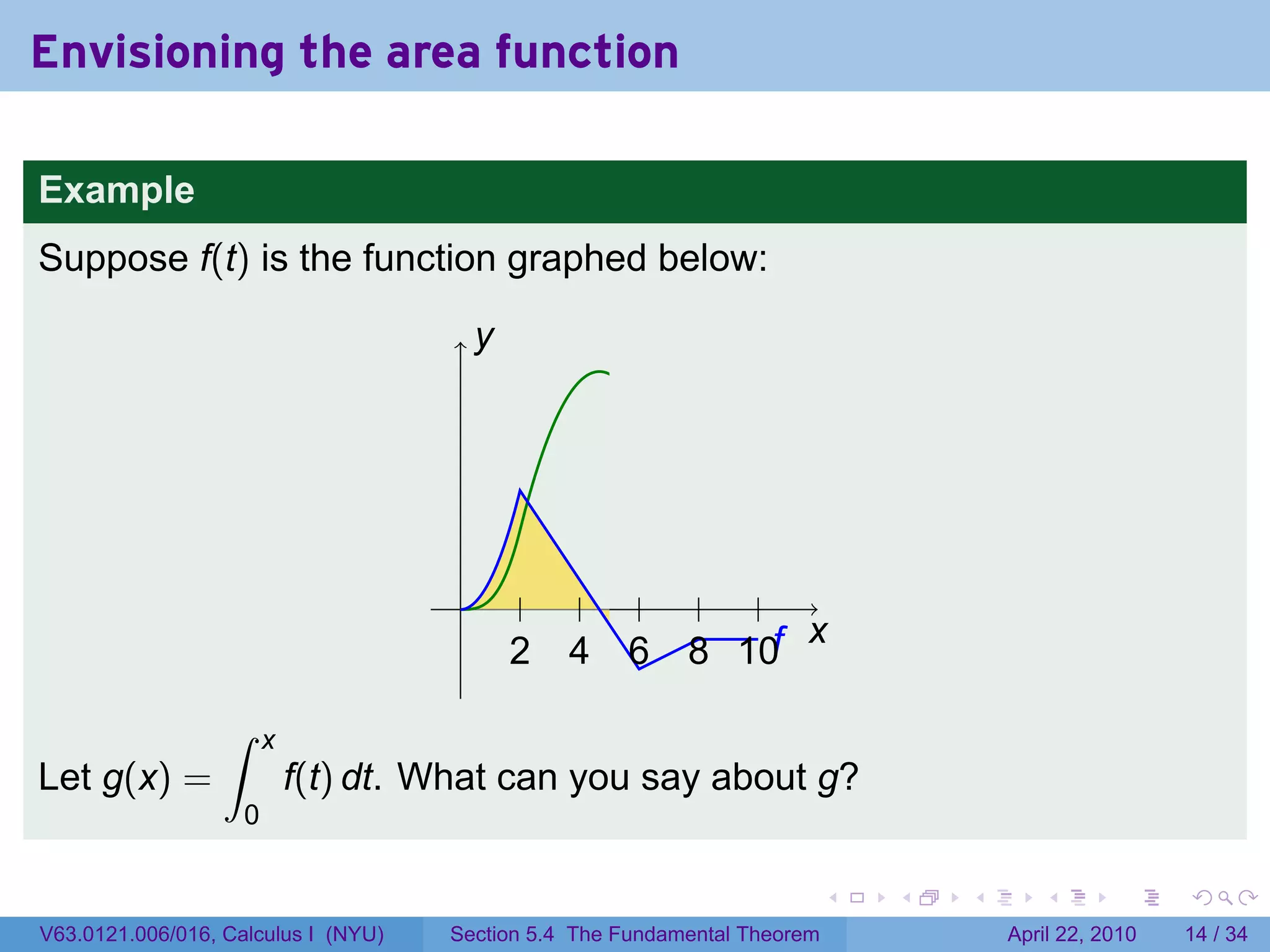
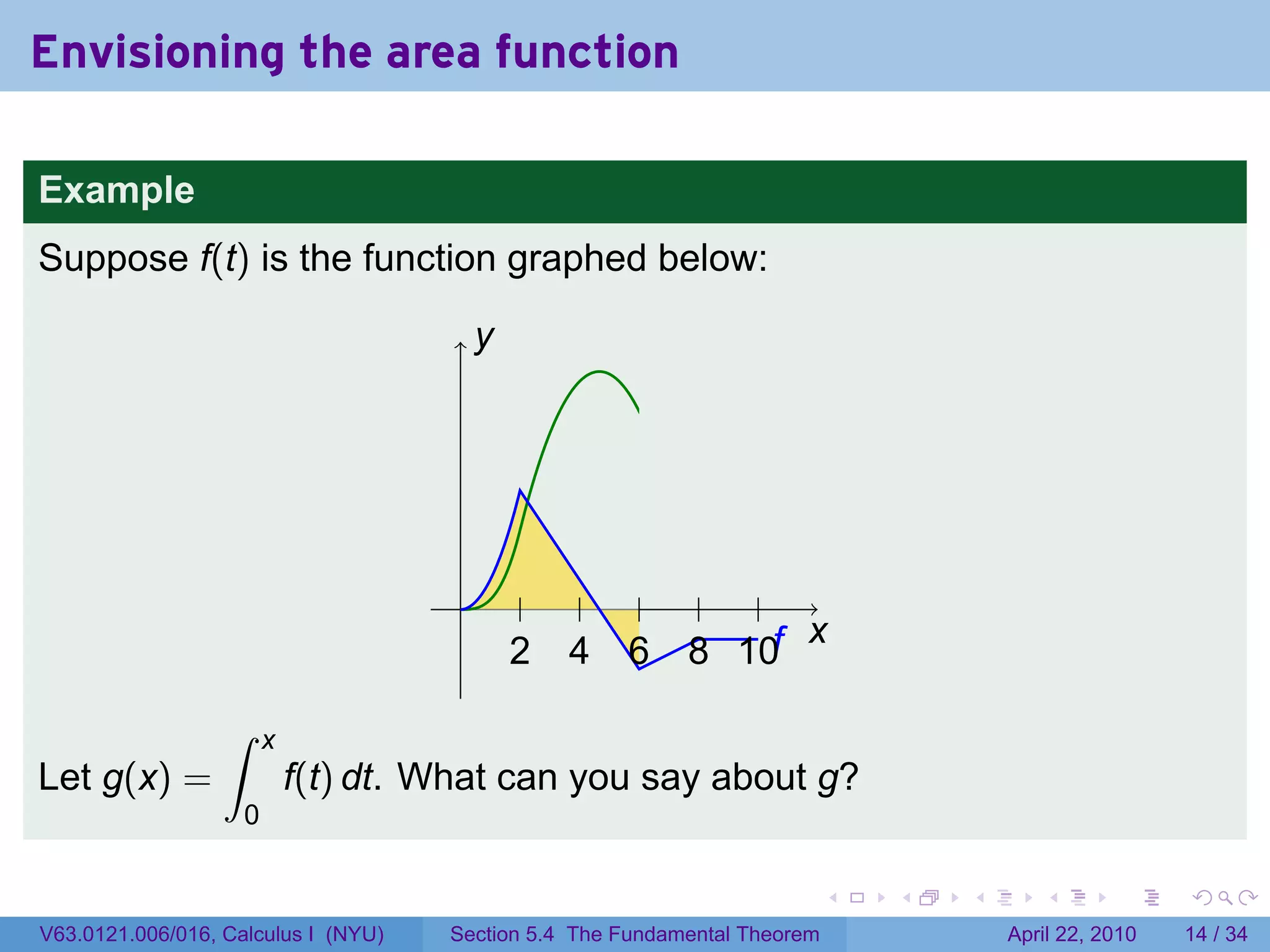
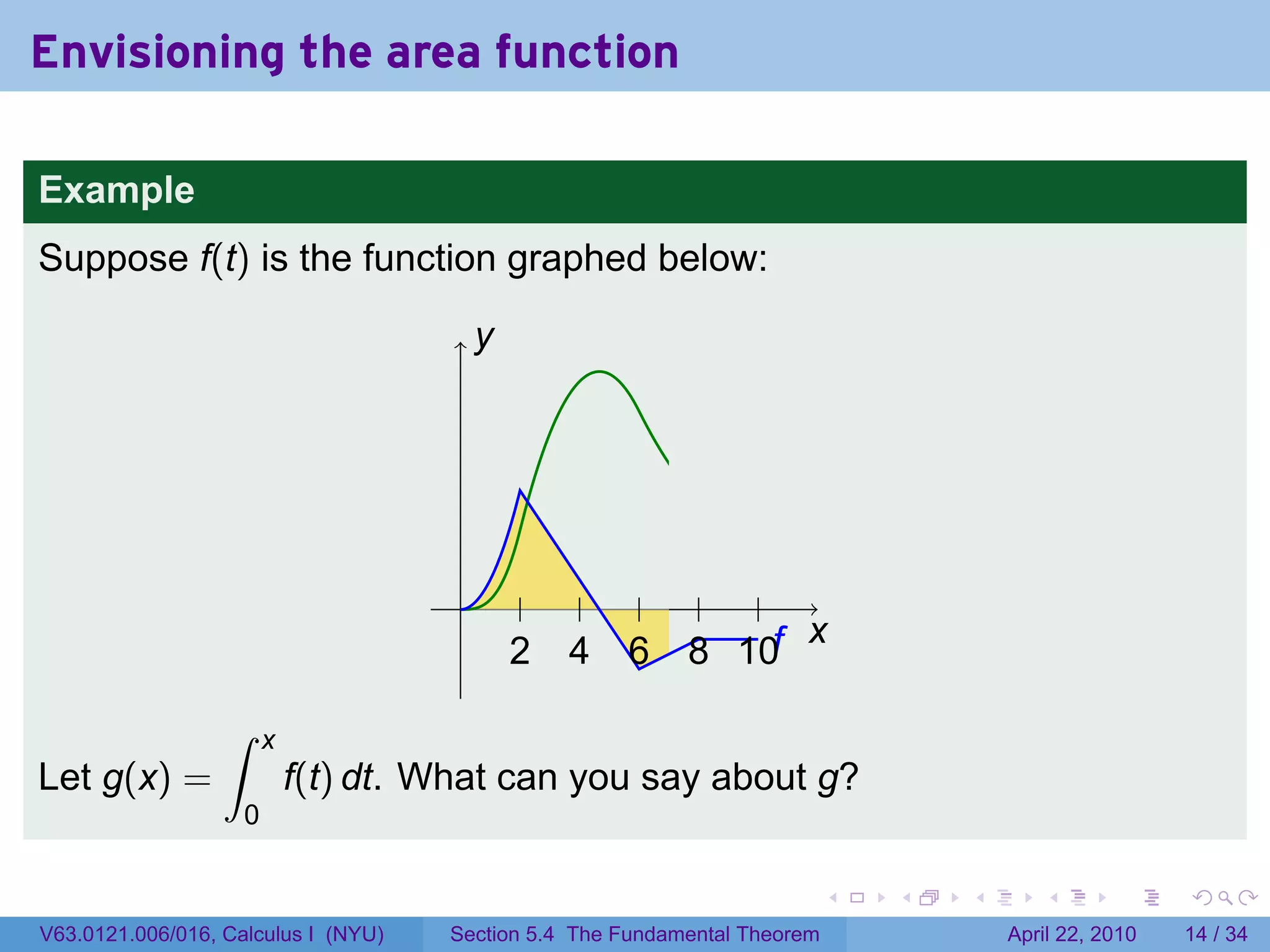
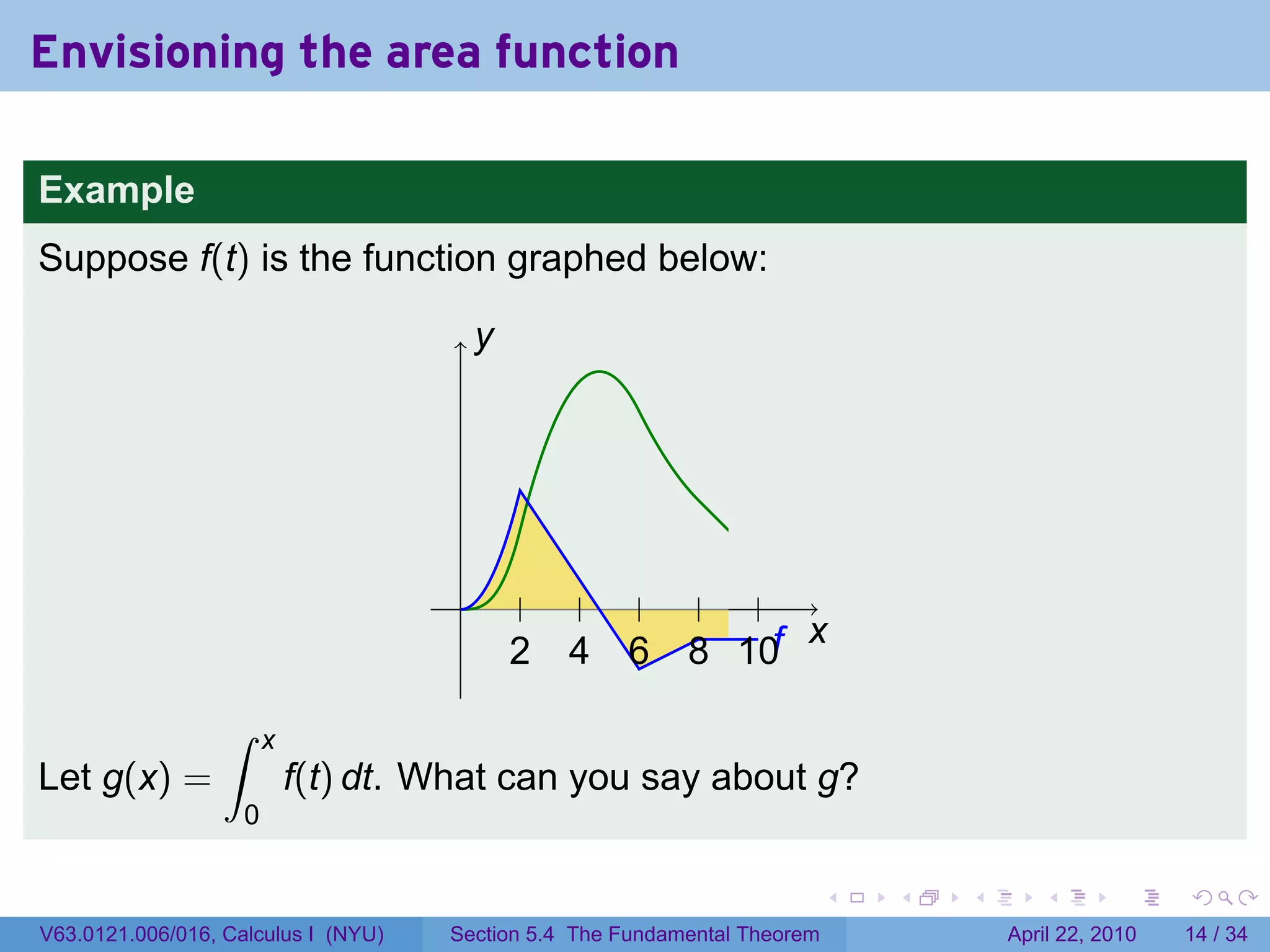
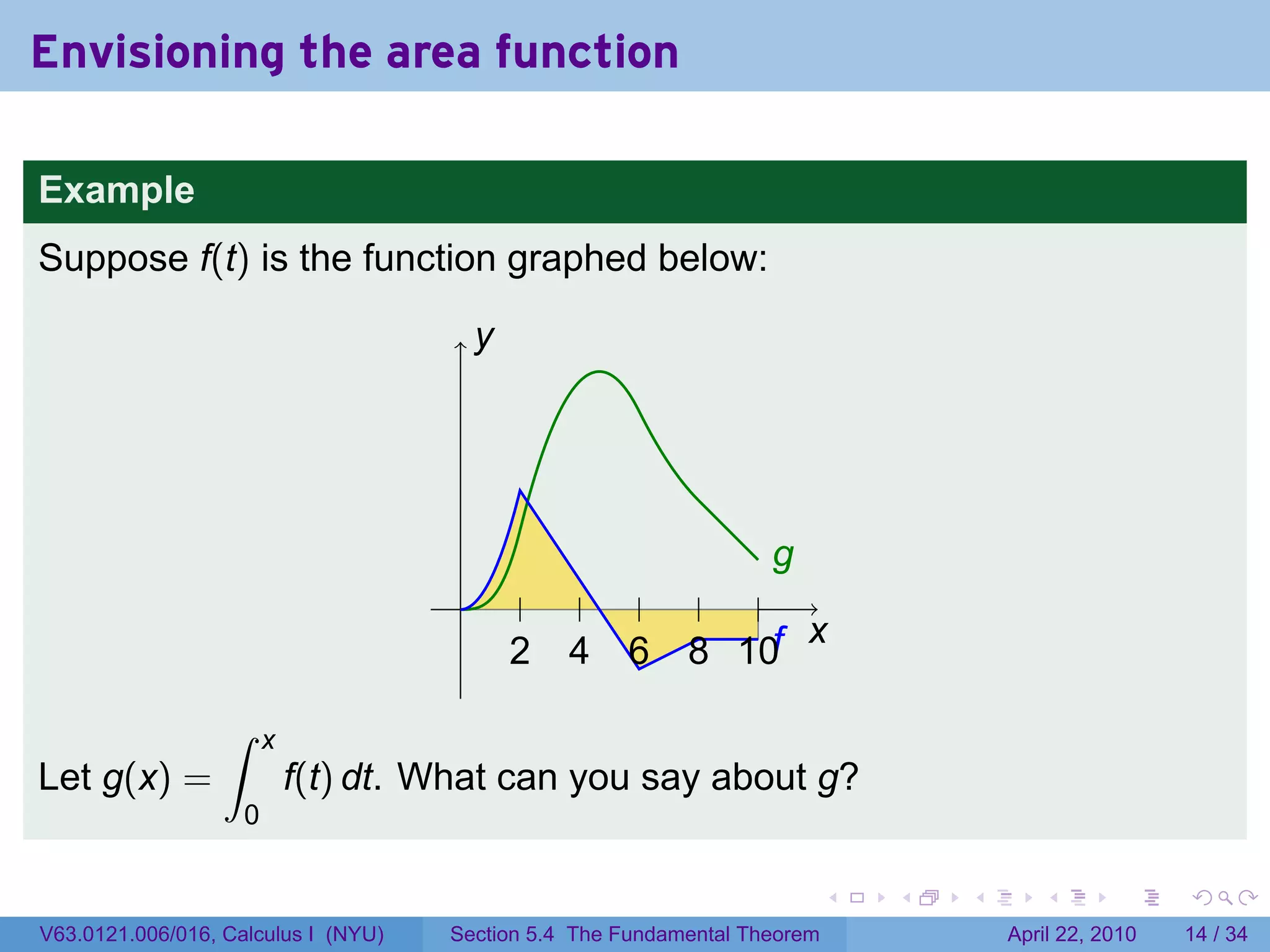
The area function

Let f be a function which is integrable (i.e., continuous or with finitely
many jump discontinuities) on [a, b]. Define
∫ x
g(x) = f(t) dt.
a

The variable is x; t is a “dummy” variable that’s integrated over.
Picture changing x and taking more of less of the region under the
curve.
Question: What does f tell you about g?

. . . . . .


Envisioning the area function

Example
Suppose f(t) is the function graphed below:
..
y

.

. . . . . . .
. x
.
2
. 4
. 6
.. 8 1f
. . 0.
∫ x
Let g(x) = f(t) dt. What can you say about g?
0

. . . . . .


Envisioning the area function

Example
Suppose f(t) is the function graphed below:
..
y

.
g
.
. . . . . . .
. x
.
2
. 4
. 6
.. 8 1f
. . 0.
∫ x
Let g(x) = f(t) dt. What can you say about g?
0

. . . . . .


features of g from f

..
y
Interval sign monotonicity monotonicity concavity
. of f of g of f of g
g
.
. . . . . . . [0, 2] + ↗ ↗ ⌣
. ..fx
. . .. . . 0
2 4 6 81 [2, 4.5] + ↗ ↘ ⌢
[4.5, 6] − ↘ ↘ ⌢
[6, 8] − ↘ ↗ ⌣
[8, 10] − ↘ → none

. . . . . .


features of g from f

..
y
Interval sign monotonicity monotonicity concavity
. of f of g of f of g
g
.
. . . . . . . [0, 2] + ↗ ↗ ⌣
. ..fx
. . .. . . 0
2 4 6 81 [2, 4.5] + ↗ ↘ ⌢
[4.5, 6] − ↘ ↘ ⌢
[6, 8] − ↘ ↗ ⌣
[8, 10] − ↘ → none

We see that g is behaving a lot like an antiderivative of f.

. . . . . .


Theorem (The First Fundamental Theorem of Calculus)
Let f be an integrable function on [a, b] and define
∫ x
g(x) = f(t) dt.
a

If f is continuous at x in (a, b), then g is differentiable at x and

g′ (x) = f(x).

. . . . . .


Proving the Fundamental Theorem

Proof.
Let h > 0 be given so that x + h < b. We have

g(x + h) − g(x)
=
h

. . . . . .



Proof.
∫
g(x + h) − g(x) 1 x+h
= f(t) dt.
h h x

. . . . . .



Proof.
∫
g(x + h) − g(x) 1 x+h
= f(t) dt.
h h x

Let Mh be the maximum value of f on [x, x + h], and let mh the minimum
value of f on [x, x + h]. From §5.2 we have
∫ x+h
f(t) dt
x

So
g(x + h) − g(x)
mh ≤ ≤ Mh .
h

. . . . . .



Proof.
∫
g(x + h) − g(x) 1 x+h
= f(t) dt.
h h x

∫ x+h
f(t) dt ≤ Mh · h
x

So
g(x + h) − g(x)
mh ≤ ≤ Mh .
h
As h → 0, both mh and Mh tend to f(x).
. . . . . .



Proof.
∫
g(x + h) − g(x) 1 x+h
= f(t) dt.
h h x

∫ x+h
mh · h ≤ f(t) dt ≤ Mh · h
x

So
g(x + h) − g(x)
mh ≤ ≤ Mh .
h
As h → 0, both mh and Mh tend to f(x).
. . . . . .


Meet the Mathematician: James Gregory

Scottish, 1638-1675
Astronomer and Geometer
Conceived transcendental
numbers and found
evidence that π was
transcendental
Proved a geometric
version of 1FTC as a
lemma but didn’t take it
further

. . . . . .


Meet the Mathematician: Isaac Barrow

English, 1630-1677
Professor of Greek,
theology, and mathematics
at Cambridge
Had a famous student

. . . . . .


Meet the Mathematician: Isaac Newton

English, 1643–1727
Professor at Cambridge
(England)
Philosophiae Naturalis
Principia Mathematica
published 1687

. . . . . .


Meet the Mathematician: Gottfried Leibniz

German, 1646–1716
Eminent philosopher as
well as mathematician
Contemporarily disgraced
by the calculus priority
dispute

. . . . . .


Differentiation and Integration as reverse processes
Putting together 1FTC and 2FTC, we get a beautiful relationship
between the two fundamental concepts in calculus.
Theorem (The Fundamental Theorem(s) of Calculus)

I. If f is a continuous function, then
∫ x
d
f(t) dt = f(x)
dx a

So the derivative of the integral is the original function.
II. If f is a differentiable function, then
∫ b
f′ (x) dx = f(b) − f(a).
a

So the integral of the derivative of is (an evaluation of) the original
function.
. . . . . .


Outline


The Area Function
Biographies

Erf
Other applications

. . . . . .


Differentiation of area functions
Example
∫ 3x
Let h(x) = t3 dt. What is h′ (x)?
0

. . . . . .


Example
∫ 3x
0

Solution (Using 2FTC)
3x
t4 1
h(x) = = (3x)4 = 1
4 · 81x4 , so h′ (x) = 81x3 .
4 4
0

. . . . . .


Example
∫ 3x
0

3x
t4 1
h(x) = = (3x)4 = 1
4 · 81x4 , so h′ (x) = 81x3 .
4 4
0

∫ u
We can think of h as the composition g k, where g(u) = ◦ t3 dt and
0
k(x) = 3x.

. . . . . .


Example
∫ 3x
0

3x
t4 1
h(x) = = (3x)4 = 1
4 · 81x4 , so h′ (x) = 81x3 .
4 4
0

∫ u
We can think of h as the composition g k, where g(u) = ◦ t3 dt and
0
k(x) = 3x. Then h′ (x) = g′ (u) · k′ (x), or

h′ (x) = g′ (k(x)) · k′ (x) = (k(x))3 · 3 = (3x)3 · 3 = 81x3 .
. . . . . .


Differentiation of area functions, in general

by 1FTC
∫ k(x)
d
f(t) dt = f(k(x))k′ (x)
dx a
by reversing the order of integration:
∫ b ∫ h(x)
d d
f(t) dt = − f(t) dt = −f(h(x))h′ (x)
dx h(x) dx b

by combining the two above:
∫ (∫ ∫ )
k(x) k(x) 0
d d
f(t) dt = f(t) dt + f(t) dt
dx h(x) dx 0 h(x)

= f(k(x))k′ (x) − f(h(x))h′ (x)

. . . . . .


Example
∫ sin2 x
Let h(x) = (17t2 + 4t − 4) dt. What is h′ (x)?
0

. . . . . .


Example
∫ sin2 x
0

Solution
We have
∫ sin2 x
d
(17t2 + 4t − 4) dt
dx 0
( ) d
= 17(sin2 x)2 + 4(sin2 x) − 4 · sin2 x
( ) dx
= 17 sin4 x + 4 sin2 x − 4 · 2 sin x cos x

. . . . . .


Example
∫ sin2 x
3

. . . . . .


Example
∫ sin2 x
3

Solution
We have
∫ sin2 x
d
(17t2 + 4t − 4) dt
dx 0
( ) d
= 17(sin2 x)2 + 4(sin2 x) − 4 · sin2 x
( ) dx
= 17 sin4 x + 4 sin2 x − 4 · 2 sin x cos x

. . . . . .


Question
Why is
∫ sin2 x ∫ sin2 x
d d
(17t2 + 4t − 4) dt = (17t2 + 4t − 4) dt?
dx 0 dx 3

Or, why doesn’t the lower limit appear in the derivative?

. . . . . .


Question
Why is
∫ sin2 x ∫ sin2 x
d d
(17t2 + 4t − 4) dt = (17t2 + 4t − 4) dt?
dx 0 dx 3

Or, why doesn’t the lower limit appear in the derivative?

Answer
Because
∫ sin2 x ∫ 3 ∫ sin2 x
2
(17t + 4t − 4) dt = 2
(17t + 4t − 4) dt + (17t2 + 4t − 4) dt
0 0 3

So the two functions differ by a constant.

. . . . . .


Example
∫ ex
Find the derivative of F(x) = sin4 t dt.
x3

. . . . . .


Example
∫ ex
x3

Solution
∫ ex
d
sin4 t dt = sin4 (ex ) · ex − sin4 (x3 ) · 3x2
dx x3

. . . . . .


Example
∫ ex
x3

Solution
∫ ex
d
sin4 t dt = sin4 (ex ) · ex − sin4 (x3 ) · 3x2
dx x3

Notice here it’s much easier than finding an antiderivative for sin4 .

. . . . . .


Why use 1FTC?

Question
Why would we use 1FTC to find the derivative of an integral? It seems
like confusion for its own sake.

. . . . . .


Why use 1FTC?

Question

Answer

Some functions are difficult or impossible to integrate in
elementary terms.

. . . . . .


Why use 1FTC?

Question

Answer

Some functions are difficult or impossible to integrate in
elementary terms.
Some functions are naturally defined in terms of other integrals.

. . . . . .


Erf
Here’s a function with a funny name but an important role:
∫ x
2
e−t dt.
2
erf(x) = √
π 0

. . . . . .


Erf
∫ x
2
e−t dt.
2
erf(x) = √
π 0
It turns out erf is the shape of the bell curve.

. . . . . .


Erf
∫ x
2
e−t dt.
2
erf(x) = √
π 0
It turns out erf is the shape of the bell curve. We can’t find erf(x),
explicitly, but we do know its derivative: erf′ (x) =

. . . . . .


Erf
∫ x
2
e−t dt.
2
erf(x) = √
π 0
2
explicitly, but we do know its derivative: erf′ (x) = √ e−x .
2

π

. . . . . .


Erf
∫ x
2
e−t dt.
2
erf(x) = √
π 0
2
2

π
Example
d
Find erf(x2 ).
dx

. . . . . .


Erf
∫ x
2
e−t dt.
2
erf(x) = √
π 0
2
2

π
Example
d
Find erf(x2 ).
dx

Solution
By the chain rule we have

d d 2 4
erf(x2 ) = erf′ (x2 ) x2 = √ e−(x ) 2x = √ xe−x .
2 2 4

dx dx π π
. . . . . .


Other functions defined by integrals

The future value of an asset:
∫ ∞
FV(t) = π(τ )e−rτ dτ
t

where π(τ ) is the profitability at time τ and r is the discount rate.
The consumer surplus of a good:
∫ q∗
∗
CS(q ) = (f(q) − p∗ ) dq
0

where f(q) is the demand function and p∗ and q∗ the equilibrium
price and quantity.

. . . . . .


Surplus by picture

c
. onsumer surplus
p
. rice (p)

s
. upply

.∗ .
p . . quilibrium
e

d
. emand f(q)
. .
.∗
q q
. uantity (q)

. . . . . .


Summary

Functions defined as integrals can be differentiated using the first
FTC: ∫ x
d
f(t) dt = f(x)
dx a
The two FTCs link the two major processes in calculus:
differentiation and integration
∫
F′ (x) dx = F(x) + C

Follow the calculus wars on twitter: #calcwars

. . . . . .


Fundamental Theorem Calculus Notes

Recommended

Recommended

More Related Content

What's hot

What's hot (18)

Similar to Fundamental Theorem Calculus Notes

Similar to Fundamental Theorem Calculus Notes (20)

More from Matthew Leingang

More from Matthew Leingang (20)

Fundamental Theorem Calculus Notes