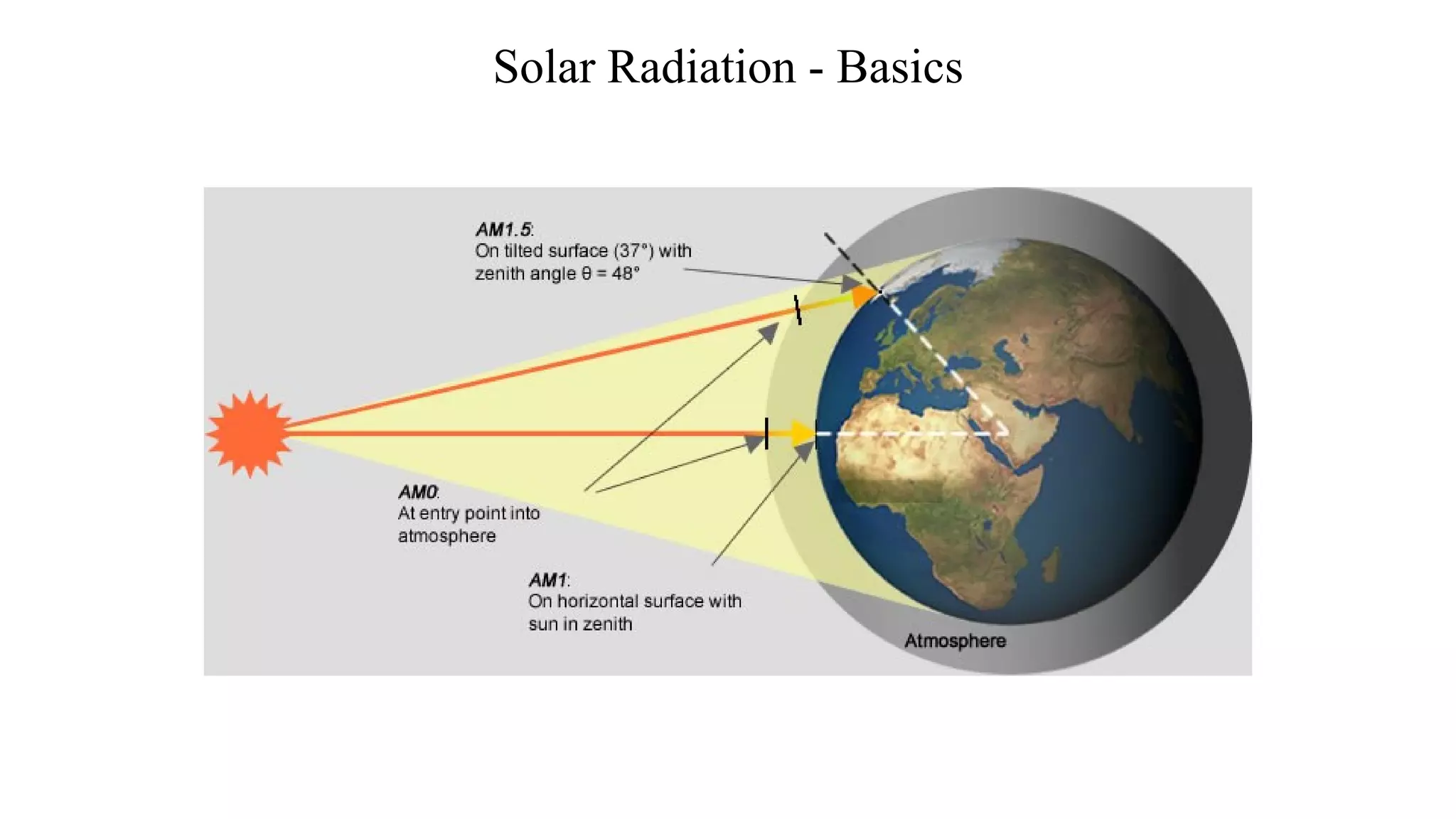
This document discusses solar energy basics including solar radiation, solar resource assessment, and solar geometry. Some key points: - Solar radiation received on Earth consists of direct beam and diffuse radiation after passing through the atmosphere. The amount of each component depends on factors like air mass and atmospheric conditions. - Solar geometry concepts like zenith angle, declination, and hour angle are used to determine the direction of incoming solar radiation and calculate quantities like duration of sunshine. - Equations are provided to calculate the angle of incidence of direct radiation on tilted surfaces, as well as the total solar radiation received, accounting for direct beam, diffuse sky, and ground-reflected components.

1. Solar Energy – Basics,
Solar Thermal Energy
and Power Generation

2. Solar Radiation - Basics
• Solar energy is essentially electromagnetic radiation emitted by the
photosphere of the Sun at a temperature of about 5800 K.
• Diameter of the sun = 1.392 x 106 km
• Average sun‐earth distance = 1.5 x 108 km
• Angle subtended by solar disc on earth
• = 32 minutes

3. Solar Radiation - Basics

4. Some Issues Regarding Solar Resource on Earth
• Electromagnetic radiation from a distantly located hot surface
(photosphere) radiating (almost) like a black body at a temperature of
5762 K ±50 K (effective black body temperature)
Spectral distribution of radiation emitted by the photosphere
Fraction of incident solar energy in Ultra Violet, Visible and Infra Red
wavelength ranges

5. Solar Radiation - Basics

6. Wein’s Displacement Law
• The wavelength ( λmax) corresponding to maximum intensity of
blackbody radiation
λmaxT = 2897.8 μmK
λmax is higher at lower temperature ,or
For bodies operating at higher temperatures the wavelength
corresponding to maximum intensity would be small

7. Solar Constant
• Energy from the sun (integrated overall wave lengths) per unit time,
received on a unit area of surface perpendicular to the direction of
propagation of the radiation, at the earth’s mean distance from the sun,
outside the earth’s surface.
GSC = 1367 W/m2

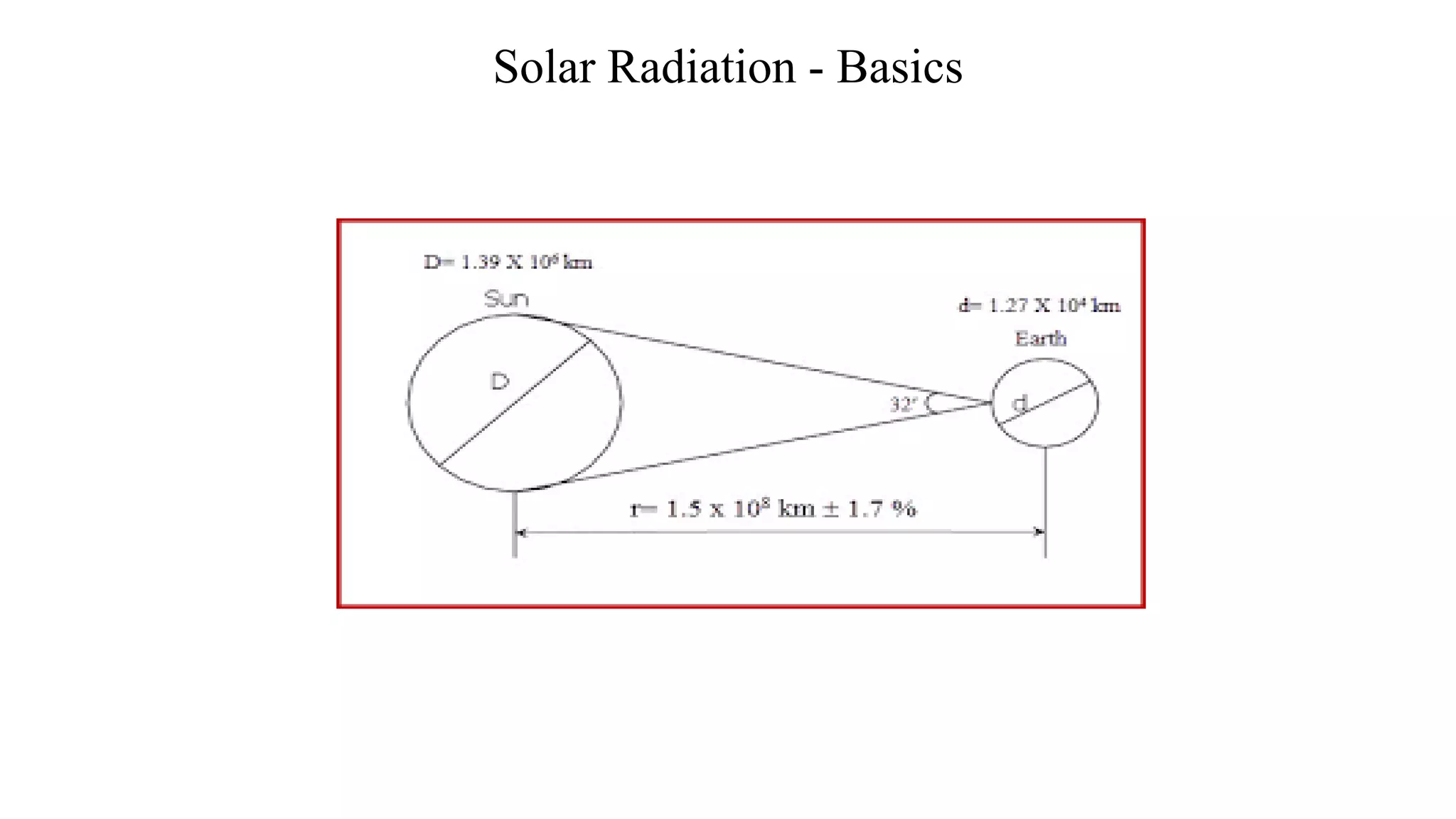
8. Extra‐terrestrial Solar Radiation
• Solar radiation just outside the earth’s atmosphere
• Change in the value of extra‐terrestrial solar radiation just outside the
earth’s atmosphere due to change in earth‐sun distance
• Extraterrestrial Solar Radiation: Solar Constant
GON = GSC [ 1+ 0.033 cos (360 n/ 365)]

9. Variation of Extra-terrestrial Solar Radiation
• Variation in the radiation emitted by the Sun itself (± 1.5%)
• Variation of the Earth-Sun distance arising from Earth’s slightly elliptic
path (± 3.0%)

10. Terrestrial Solar Radiation
• Solar radiation available on the surface of earth (after passage through
its atmosphere)
• Earth’s atmosphere has gases (nitrogen, oxygen, carbon dioxide, ozone,
water vapour, dust and other particulate matter…)
• As solar radiation passes through the earth’s atmosphere
(i) ABSORPTION and (ii) SCATTERING take place

11. Terrestrial Solar Radiation
• Absorption (due to ozone, carbon dioxide, water vapour etc.) reduces
the intensity of solar radiation and also changes its spectral distribution
• Scattering of solar radiation (due to its interaction with dust particles,
molecules etc.) changes the direction of solar radiation.

12. Atmospheric Attenuation of Solar radiation
If it is assumed that the attenuation is proportional to the local intensity in the medium
and also to the distance traversed, then
‐dI α I (intensity of beam radiation at the point)
α dx(incremental distance traversed through the medium)
Or dI= ‐K I dx (where the constant of proportionality, K, is the EXTINCTION
COEFFICIENT for the air /atmosphere )
Thus dI/I = ‐K dx
Upon integration log I = ‐K x + C
Using the condition that at x = 0, I = I(0), C = log I(0)
log I –log I(0) = ‐K x which gives I = I(0) exp (‐K x)
kx
-
0
kx
-
0
e
I
I
or
e
I
I



13. Variation of Extra-terrestrial Solar Radiation

14. Solar Resource: Terrestrial Radiation
Thus a surface on earth may receive two types of solar radiation:
(a) Direct (or Beam) component of solar radiation that reached directly as
a beam to the surface without getting scattered (no change in the
direction)
(b) Diffuse component of solar radiation that reaches the surface after
scattering and as a consequence a change in the direction (change in
direction due to scattering is random)

15. Solar Resource: Terrestrial Radiation
Total solar radiation = Direct + Diffuse components of solar radiation
• Optically sensitive surfaces and collection of diffuse component of solar
radiation
Mirrors and Lenses
Diffuse fraction in total solar radiation and feasibility of
using mirrors and lenses for solar energy collection

16. Air Mass
If L0 is the vertical thickness of atmosphere, thickness (L’) of the
atmosphere through which beam radiation passes when the sun is at
zenith angle θz
L’ = L sec (θz)
Air mass (AM) is defined as the ratio of the optical thickness of the
atmosphere through which the beam radiation passes to the optical
thickness if the sun were at zenith
Thus, AM = L’/L = sec(θz)

17. Solar Radiation - Basics

18. Air Mass
• Thus Air Mass (Ratio) is the dimensionless path length of beam solar
radiation through the atmosphere
Air Mass Symbol Comments
0 AM 0 Extra-terrestrial solar radiation
1 AM 1 Sun is overhead (at Zenith)
2 AM 2 Zenith angle is 60°

19. Solar Resource: Terrestrial Radiation
• Diffuse component of solar radiation in the incident solar radiation is
expected to be more if
(a) the radiation has to travel longer distance through the earth’s
atmosphere
(b) the atmosphere has clouds (dark), the air has lot of dust and other
particulates
• The solar radiation travels minimum thickness of the earth’s atmosphere
when the sun is overhead. In the mornings and afternoons it has to travel
longer distance through the atmosphere

20. Solar Resource: Terrestrial Radiation
• It is possible to exactly calculate the direction of incidence of beam
(direct) component of solar radiation (with the knowledge of the sun
earth geometry)
It is possible to orient a surface towards the direction of incidence
of the beam solar radiation to maximize its collection

21. Solar Resource: Terrestrial Radiation
• Since the diffuse component of solar radiation may be contributed from
any direction of the sky, it is not possible to specify any particular
direction of its incidence
Optical elements (such as mirrors and lenses) that follow laws of
reflection and/or refraction will not be efficient in collecting
diffuse component of solar radiation
Unsuitability of solar concentrators at places with higher fraction of
diffuse component of solar radiation

22. Solar Radiation Geometry
• Latitude (φ) – angle between the earth’s equatorial plane and a line
from the centre of the earth to the site/ location
• Declination (δ) – angular displacement of the Sun from the plane of
earth’s equator
• Hour angle (ω) – angle through which the earth must turn to bring
meridian of the observer directly in line with Sun’s rays

23. B1.3 Nature of the solar resource
Solar geometry
Beam
radiation
f
d

24. d = Declination
n = day number
(number of
days since 1st
January)
Solar Radiation Geometry
284
23.45sin 360
365
n
d

 
  
 

26. Variation of Declination angle

27. Variation of Declination angle

28. Variation of Hour Angle

29. Solar Time
• It is measured with respect to solar noon.
• Solar noon is the time when the sun crosses the observer’s meridian–i.e.
local longitude
• The difference between two consecutive solar noons defines a solar
day.
• Because of precession of the earth’s axis and orbital and rotational
variations, a solar day is not always of twenty four hours duration
Difficulty in using a clock according to solar time

30. Solar Noon and Solar Time
• As the earth moves on its axis there is time when the sun is located just
above the longitude (meridian) of the location
• This time is called SOLAR NOON at that location and the Hour Angle
(ω) is determined with respect to Solar Noon.
• The Solar Noon could be different from the Standard Noon as indicated
by the clocks as the standard times of a time zone are based on the Solar
Noon at a specific location.
Need to correct the standard time as defined by a clock for the difference
in the longitudes of the location of interest and the location for which the
standard time is set

31. Solar Noon and Solar Time
Two corrections are required to convert standard time to solar time:
• Longitude Correction: for the difference between the local (observer’s)
longitude and the Standard longitude (for the time zone) –this correction
can be positive or negative
• Equation of Time: for perturbation in the rate of rotation of earth, thus
affecting the length of Solar Day
• If the location is on the EAST of Standard longitude, the sun has
already passed through the local longitude by the time solar noon occurs
• If the location is on the WEST of Standard longitude, the sun would
reach the local longitude some time after the solar noon

32. Solar Noon and Solar Time

33. Solar Noon and Solar Time
Solar Time = Standard time ± 4 (Standard time longitude – longitude of
location) + E
(Negative for eastern hemisphere and Positive for western hemisphere)

34. Solar Noon and Solar Time
Example : Determine Solar time at New Delhi and Guwahati on July 1 at
2:30 pm
(Equation of time correction on July 1 is (-) 3.5 min
New Delhi
Solar time = 1430 hrs – 4 (82.5 – 77.1) – 3.5 = 1430 – 21.6 – 3.5 = 1405 hrs
Guwahati
Solar time = 1430 hrs – 4 (82.5 – 91.73) – 3.5 = 1430 + 36.92 – 3.5 = 1503 hrs

35. Derived Angles
z
s
s
N
South E
W
Zenith

36. Solar geometry: Sun angles
z = Zenith angle – the angle between the vertical (zenith) and
the line of the sun
αs = Solar attitude angle – the angle between the horizontal and
the line to the sun
γs = Solar azimuth angle – the angle of the projection of beam
radiation on the horizontal plane (with zero due south, east
negative and west positive)

37. Solar geometry: Collector angles
z

s
s


N
South
E
W
Zenith

38. Solar geometry: Collector angles
 = Slope – the angle between the plane of the collector and the
horizontal
g = Surface azimuth angle – the deviation of the projection on a
horizontal plane of the normal to the collector from the local
meridian (with zero due south, east negative and west positive)
 = Angle of incidence – the angle between the beam radiation on
the collector and the normal

39. Solar geometry: Sun angles

40. Angle of Incidence of Direct (Beam) Radiation
The equation relating the angle of incidence (θ) of direct (beam) radiation on
a flat surface (the angle between direct radiation on a surface and
normal to the surface) is as follows:
cosθ= sin δ sin φ cosβ–sin δ cosφ sin β cosγ
+ cosδ cosφ cosβ cosω + cosδsinγsinβsin ω
+ cosδ sinφ sin β cosγ cosω
θz : Zenith Angle (angle between zenith and beam solar radiation)
α: Altitude Angle of the Sun
Thus θz = 90 ‐α

41. Angle of Incidence on a Horizontal Surface
For a horizontal surface β= 0 and γ= 0. The angle of incidence of
direct solar radiation on a horizontal surface is the same as the
Zenith Angle (θz). Thus
cos θz = sin δ sin φ (1) – sin δ cos φ (0) (1) + cosδ cos φ (1) cos ω +
cosδ (0) (0) sin ω + cosδ sin φ (0) (1) cos ω
cos θz = cosδ cos φ cos ω+ sin δ sin φ

42. Angle of Incidence (θT) on a South Facing Tilted Flat Surface
cos θ= sin δ sin φcos β – sin δ cos φ sin β cos γ + cosδ cos φ cos β cos ω +
cosδ sinγ sinβ sin ω + cosδ sin φ sin β cos γ cos ω
For a south facing tilted flat surface γ=0, and thus
cos θT= sin δ sin φ cos β – sin δ cos φ sin β (1) + cosδ cos φ cos β cos ω+
cosδ (0) sinβ sin ω + cosδ sin φ sin β (1) cos ω
cos θT= sin δ{sin φcos β–cos φsin β} + cosδcos ω{cos φ cos β+ sin φsin β}
cos θT = sin δsin (φ–β) + cos (φ–β) cosδ cos ω
For comparison, angle of incidence on a horizontal surface is
cos θz = sin δ sin φ+ cos δ cos φ cos ω

43. Sunset Hour Angle and Duration of Sunshine
On a horizontal surface sun rise or sun set occurs when
θz = 90°or α= 0
If the sunset hour angle is ωs, then
Cos 90 = sin δ sin φ+ cosδ cosφ cosωs
0 = sin δ sin φ+ cosδ cosφ cosωs
cosωs= (‐) sin δ sin φ/ cosδ cosφ
= (‐) tan φ tan δ
ωs = cos‐1{(‐) tan φtan δ}
Number of daylight hours (one hour time duration is equivalent to an hour angle of
15°and number of hours from solar noon to sunset are the same as the number of
hours from sunrise to solar noon )
Duration of sunshine = (2/15) cos‐1{(‐) tan φ tan δ}

44. Sunset Hour Angle and Duration of Sunshine
Example : Determine duration of sunshine at New Delhi on Jan 1 and July 1
Angle of declination on Jan 1, δ = (-) 23.01°
Angle of declination on July 1, δ = 23.12°
Jan 1
Duration of sunshine = (2/15) cos‐1{(‐) tan φ tan δ}
Duration of sunshine = (2/15) cos‐1{(‐) tan 28.70° tan (-23.01°)}
Duration of sunshine = 10.2 hours
July 1
Duration of sunshine = (2/15) cos‐1{(‐) tan φ tan δ}
Duration of sunshine = (2/15) cos‐1{(‐) tan 28.70° tan (23.12°)}
Duration of sunshine = 13.79 hours

45. Irradiance on a horizontal surface
, cos
b b n z
G G 

,
b n
G
b
G
Gb = Beam Irradiance normal to the earth’s surface (W/m2)
Gb,n = Beam Irradiance (W/m2)
qz = Zenith angle

46. , ,
,
,
cos cos
cos cos
b t b n
b t
b b n z z
G G
R
G G
 
 
  
,
b n
G
,
b t
G
b
G
,
b n
G
B5.5 System design
Tilt: Beam radiation

47. Total Solar Radiation on (South Facing)Tilted Surfaces
Solar radiation on a tilted surface consists of
(a) Direct (beam) solar radiation
(b) Diffuse solar radiation from sky
(c) Solar radiation diffusely reflected from the ground/surface in front
of the collector

48. Total Solar Radiation on (South Facing)Tilted Surfaces
• Direct (beam) solar radiation
If Ib and Id respectively represent the beam (direct) and diffuse solar
radiation incident on a horizontal surface, the direct (beam) solar
radiation on a flat surface tilted at an angle β with the horizontal would
be equal to
= (Ib / cos θz) (cos θT) = (Ib) (Rb)

49. Total Solar Radiation on (South Facing)Tilted Surfaces
• Diffuse Radiation on a Tilted Surface
If it is assumed that the sky is a uniform source of diffuse radiation (i.e.
isotropic distribution of solar radiation) a surface tilted at slope βfrom the
horizontal has a view factor to the sky given by (1 + cos β)/2
Thus diffuse radiation on a tilted surface = Id{(1 + cos β)/2}
If β= 0 (i.e. horizontal surface) the view factor has a value of unity.
If β= 90°(i.e. vertical surface) the view factor has a value of (1/2) as a
vertical surface sees only half of the sky.

50. Total Solar Radiation on (South Facing)Tilted Surfaces
• Diffusely Reflected Solar Radiation from Ground Facing the Collector
A surface tilted with a slope β with the horizontal has a view factor of the
ground of (1 ‐cosβ)/2
If β = 0 (horizontal surface) the view factor is zero as a horizontal surface does
not view any ground.
If β= 90°, the view factor is ½
If the surroundings of the collector have a reflectance of ρg for total (Ib + Id)
solar radiation, the reflected radiation from the surroundings on the surface of
the collector is = (Ib + Id) ρg (1 ‐cosβ)/2
The value of ρg is assumed 0.2 for normal ground and 0.7 for snow covered
surfaces

51. Total Solar Radiation on (South Facing)Tilted Surfaces
The hourly value of total solar radiation (IT)on a tilted surface can be
estimated from:
IT= ( Ib ) (cos θT / cos θz) + Id{(1 + cosβ)/2} + ((Ib + Id) ρg (1 ‐ cosβ)/2
With
cos θT = sin δ sin (φ–β) + cos (φ–β) cosδ cos ω
cos θz = sin δ sin φ + cos δ cos φ cos ω
Since solar process calculations are often undertaken on an hourly basis,
the values of cos θT and cos θz are determined for the midpoints of the
hours before or after solar noon

52. Calculation of Rb
Example : Calculate Rb for a surface at latitude 40°N tilted by 30°towards south
from the horizontal for the hour 9 to 10 on February 16
Solution: φ= 40°N , β= 30°, n = 31 + 16 = 47
δ= 23.45 sin {(284 + 47)(360)/(365)} = (‐) 13°
ω= (‐)(15)(2.5) = 37.5°
Rb= (cos θT / cos θz)
Rb= {sin δ sin (φ–β) + cos(φ–β) cosδ cosω}/{sin δ sin φ+ cosδ cosφ cosω}
Rb= {sin (‐13) sin (40 –30) + cos(40 –30) cos(‐13) cos(‐37.5)}/ {sin (‐13) sin (40)+
cos(‐13) cos(40) cos(‐13)}
Rb= 1.61 (Thus the tilted surface will receive 1.61 times more direct (beam) solar
radiation as compared to horizontal surface)

53. Measurement of Solar Radiation
Pyrheliometer:
An instrument using a collimated detector for measuring solar radiation from the
sun and from a small portion of the sky around the sun (i.e. beam radiation) at
normal incidence
A pyrheliometer has a restricted view (about 5°) and is, therefore, often used to
measure the direct or beam solar radiation by pointing it towards the sun

54. Measurement of Solar Radiation
Pyranometer:
An instrument for measuring total hemispherical solar (beam + diffuse) radiation,
usually on a horizontal surface
A pyranometer has a hemispherical view of the surroundings and therefore is used to
measure total, direct and diffuse radiation on a surface
If shaded from the beam radiation by a shading ring/band or disc, a pyranometer
measures diffuse radiation from the sky

55. Pyranometers
• A pyranometer consists of a flat sensor/ detector with an un-obstructed
hemispherical view which allows it to convert and correlate the total radiation
incident on the sensor to a measurable signal
• Solar radiation detectors are of four basic types:
(a)Thermo‐mechanical
(b) Calorimetric
(c) Thermoelectric
(d) Photo‐voltaic

56. Pyranometers: Thermoelectric Detectors
• It uses a thermopile which consists of a series of thermo‐couple junctions
• The thermopile generates a voltage proportional to the temperature difference
between the hot and cold junctions, which, in turn, is proportional to the
incident solar radiation
• The pyranometer using thermal detectors for measurements can exhibit serious
errors at tilts angles from the horizontal due to free convection
• These errors are minimized by enclosing the detector in double hemispherical
high transmission glass domes
• The second dome minimizes the error due to infrared radiative exchange
between the sensor and the sky

57. Pyranometers: Thermoelectric Detectors
• A desiccator is usually provided to eliminate the effect due to condensation on
the sensor or the dome
• For measurement of diffuse radiation, the position of the shade ring is adjusted
periodically as the declination changes
• Since the shade ring obstructs some diffuse radiation from the pyranometer,
correction factors must be applied

58. Pyranometers: Photovoltaic Detectors
• These normally use silicon solar cells measuring the short circuit current
• Such detectors have the advantage of being simple in construction
• Since heat transfer is not a consideration, photovoltaic detectors do not require
clear domes or other convection suppression devices
• Photovoltaic detectors are also insensitive to the tilt as the output is not affected
by natural convection

59. Pyranometers: Photovoltaic Detectors
• One of the principal problems with photovoltaic detectors is their spectral
sensitivity/selectivity (Radiation with wavelengths greater than the band gap of the
photovoltaic detector can not be measured)
• Silicon has a band gap of 1.07 eV corresponding to a wavelength of 1.1 μm. A
significant portion of the infra‐red portion of the solar radiation has wavelength
greater than 1.1 μm (Thus, photovoltaic (silicon solar cell based) detectors are
insensitive to any changes in infra red part of solar radiation)

61. Solar Energy Utilization

62. Important Characteristics of Solar Radiation
• Low flux density
Large solar collection area
Large material requirement
High energy cost
Large space requirement
• Intermittent availability (storage, auxiliary energy supply or both)
• Radiation received from apparently moving surface
• Radiation received after passage from the atmosphere

63. Solar Thermal Technology

64. Solar Thermal Technology
• Solar radiation is converted to heat on the absorber leading to an increase in the
temperature of the absorber
• Heat collected by the absorber can be extracted from the absorber often using a
heat transfer fluid
• Heat losses occur from the absorber to the surroundings as long as it is
operating at higher temperatures than that of surroundings

65. Solar Energy Utilization
• Absorption of incident solar radiation (by an absorber)
• Minimization of thermal losses from the absorber
• Extraction of heat (from the absorber)
• Utilization of the extracted heat (for the specific end use)

66. Solar Thermal Technology: Important Issues
• How to maximize the amount of solar radiation available to the collector
(beam/ direct, diffuse, ground reflected)?
• What happens when solar radiation is incident on a surface?
• How to maximize the fraction of incident solar radiation absorbed by the
absorber surface? (How to determine the fraction of energy absorbed?)
• How to minimize heat losses from the solar collector (absorber) to the
surroundings?

67. Solar Thermal Technology: Important Issues
• How to maximize heat extraction from the solar collector?
• What decides the delivery temperature of the heat transfer fluid used for heat
extraction?
• How to obtain higher delivery temperatures of heat transfer fluids?

68. Solar Thermal Technology: Important Issues

69. Solar Thermal Technology
The temperature of the absorber surface becomes higher than that of its
surroundings upon absorption of solar radiation
Heat losses from the absorber to the surroundings by
(a) conduction
(b) convection and
(c) radiation

70. Modes of Heat Losses
Conduction:
Rate of heat loss (conduction) per unit absorber area
= (k/Δx) (Tabs–Ta)
Convection:
Rate of heat loss per unit absorber area
= (convective heat transfer coefficient)(Tabs–Ta)

71. Modes of Heat Losses

72. Approaches to Reduce Thermal Losses from the Absorber
Conduction: Put suitable thickness of good quality insulation on the un‐exposed
portion(s) of the absorber
Convection: Reduce wind speed over the absorber, preferably avoid contact of air
with the absorber surface
Radiation: Decrease emittance of the absorber surface (without compromising with
the Absorptance of the absorber for incident solar radiation)

99. Solar Photo-Voltaic Technology
• No moving parts (inherently reliable)
• Often use Silicon (2nd most redundant material on earth)
• Semiconductor industry is well developed
• Solar cells have high power to weight ratio
• No noise pollution
• No environmental emissions during operation
• Significant volume and learning effect observed

100. Solar Photo-Voltaic Technology - Components
• Photo-voltaic generator
• Mechanical support
• Tracking system
• Batteries
• Power conditioning, control and monitoring unit
• Back-up (auxiliary supply)

101. Issues with Solar Photo-Voltaic Technology
• Reflection of solar radiation (use of anti-reflection coating)
• Non-utilization of certain portion of solar spectrum (almost 23%)
• Excess energy of photons is dissipated as heat
• Losses due to recombination of electrons and holes
• Shading (self losses)

102. Types of materials used in solar cells
• Crystalline Silicon (single and multi-crystalline)
• Amorphous silicon
• Gallium arsenide
• Cadmium telluride
• Copper Indium diselimide

103. Applications
• Grid connected electricity generation
• Solar home systems
• Lanterns, micro-grid, street lighting
• Water pumping
• Refrigeration
• Transmission system powering