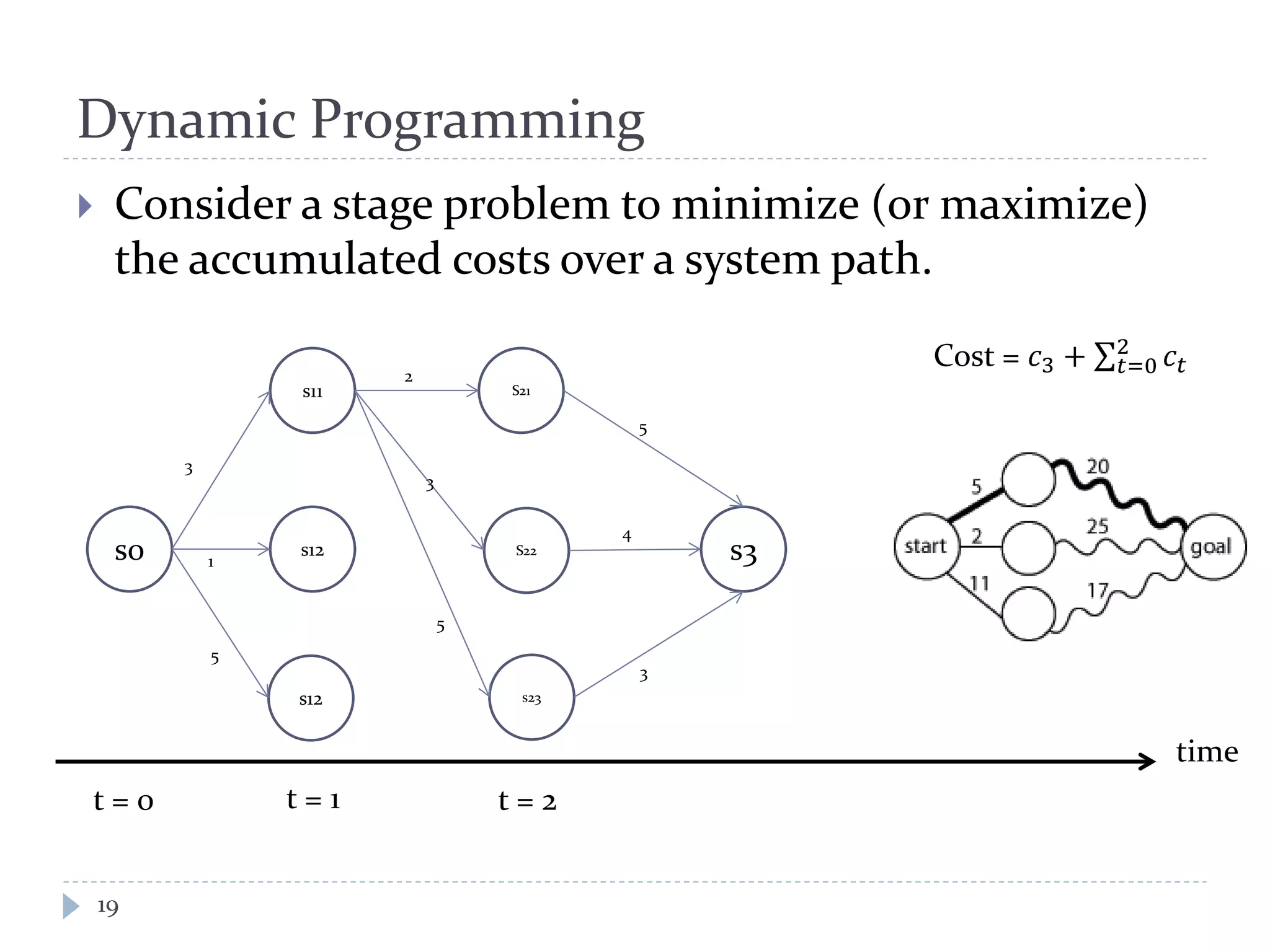
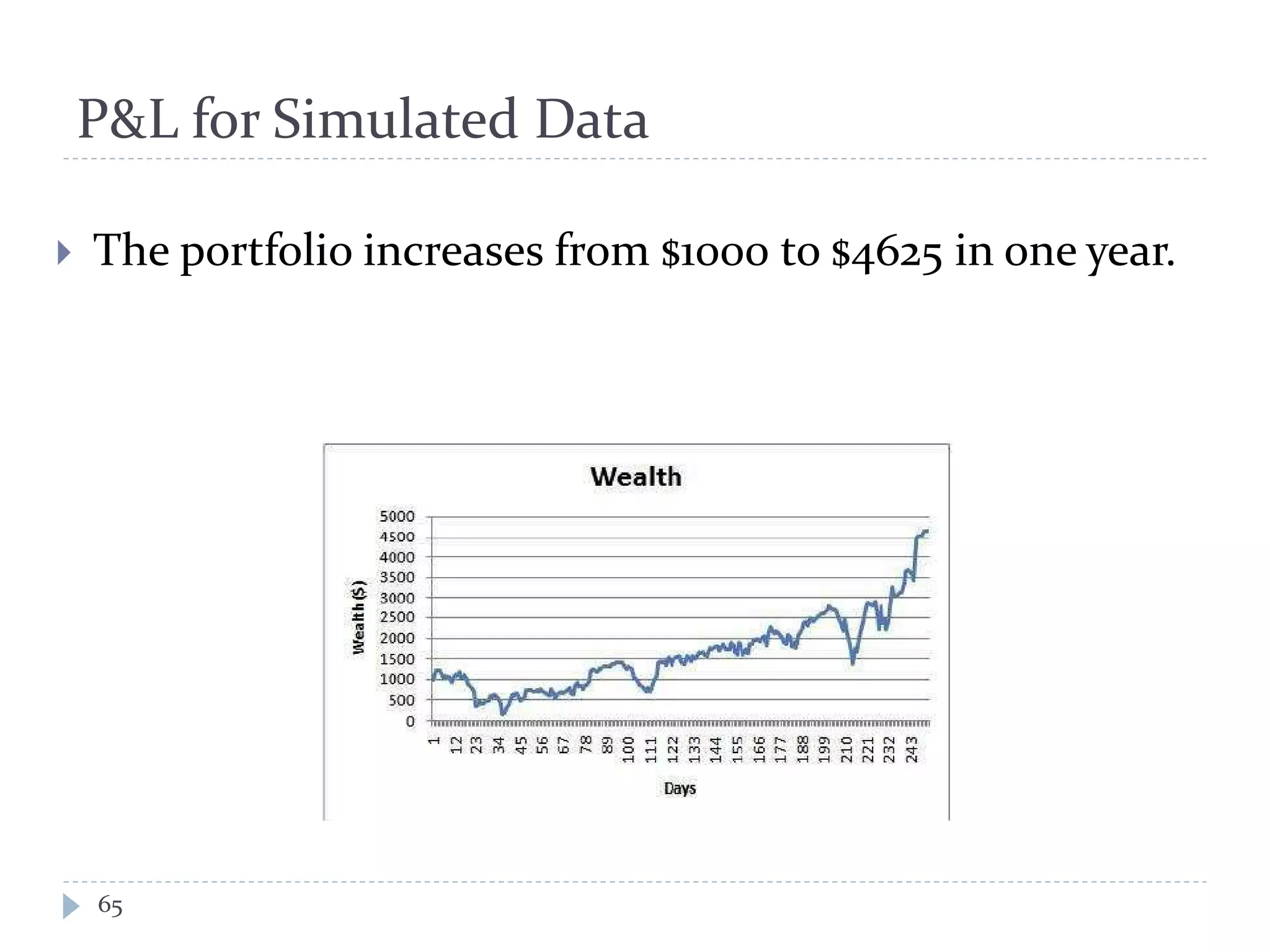
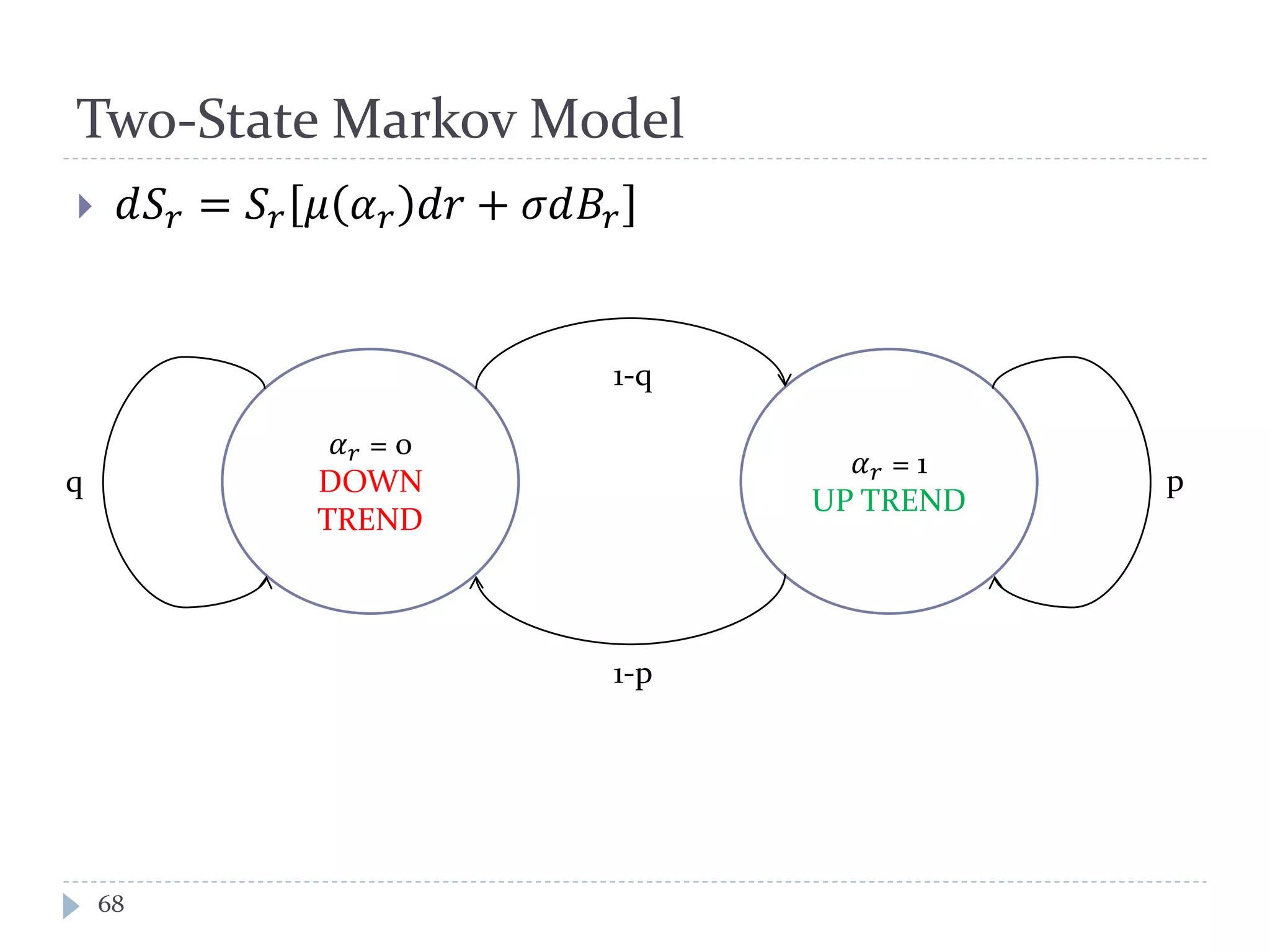
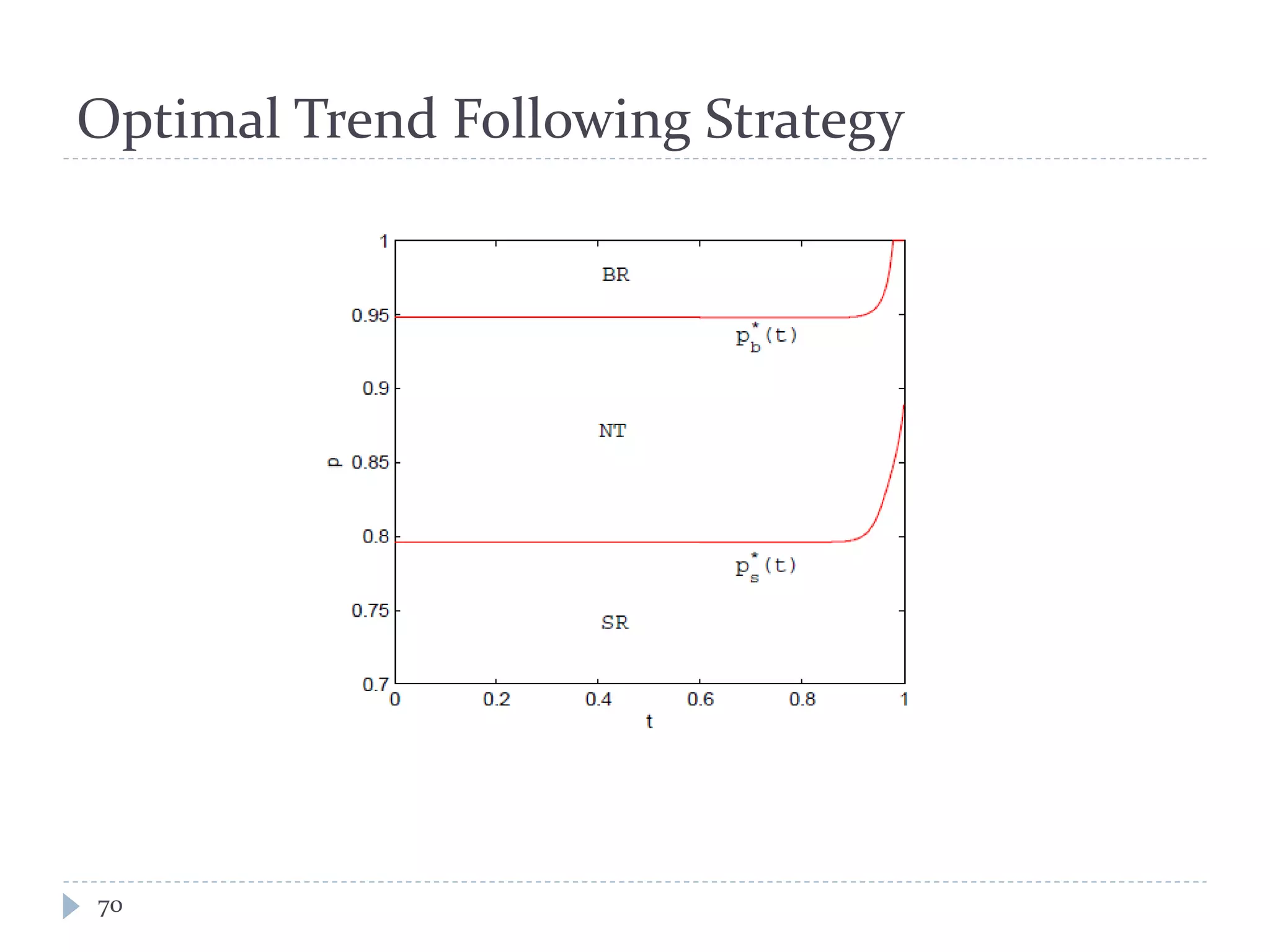
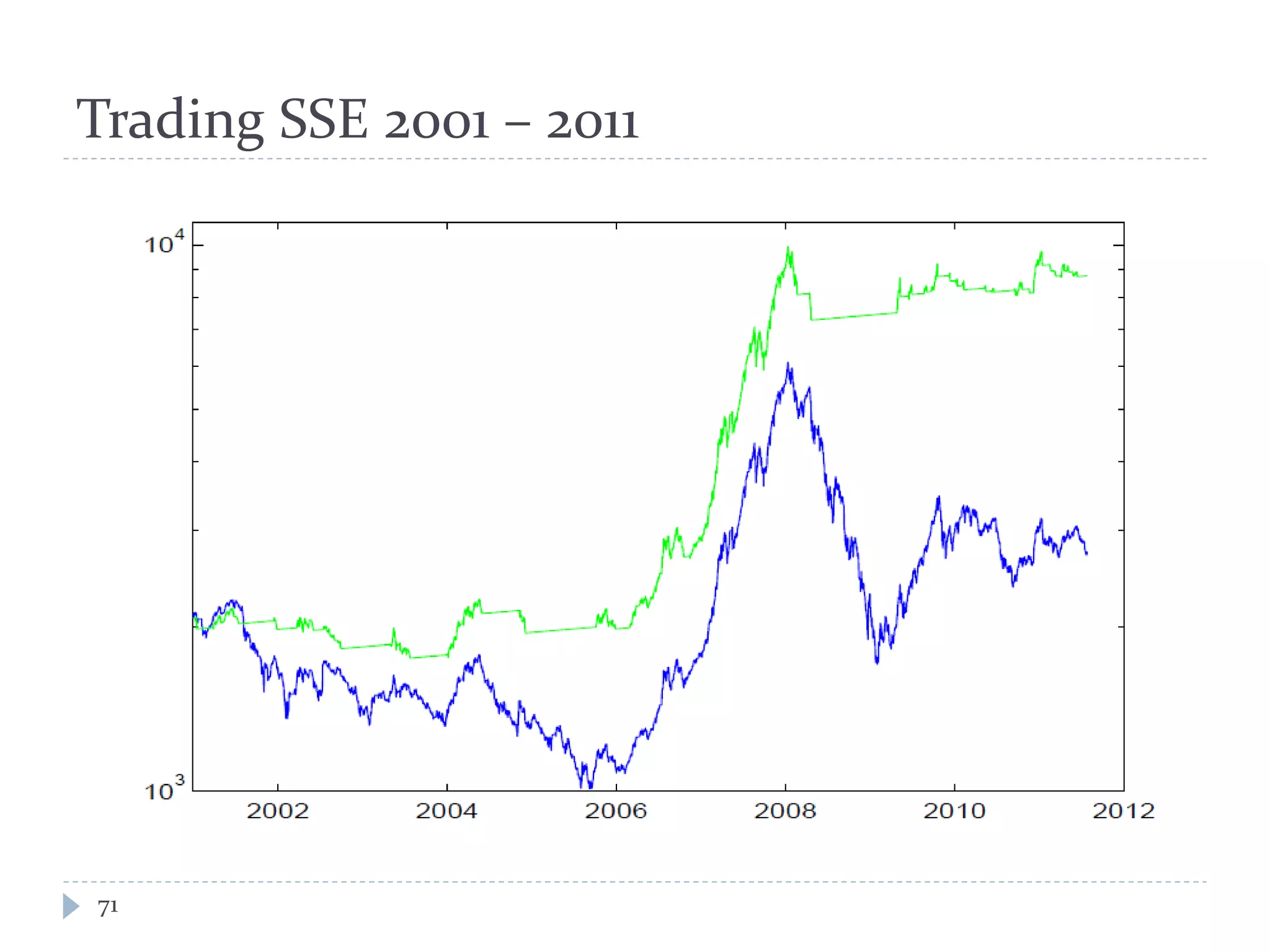
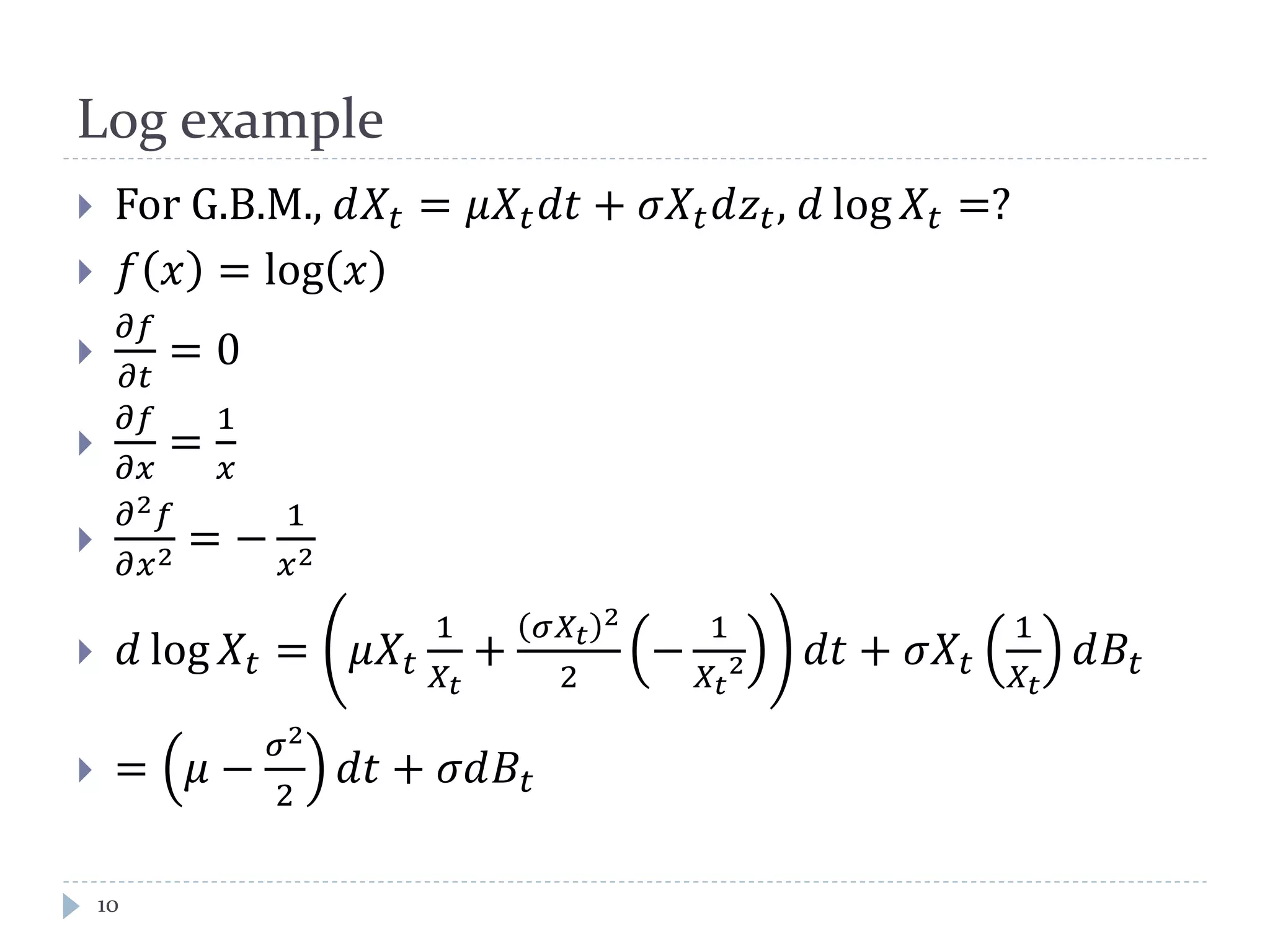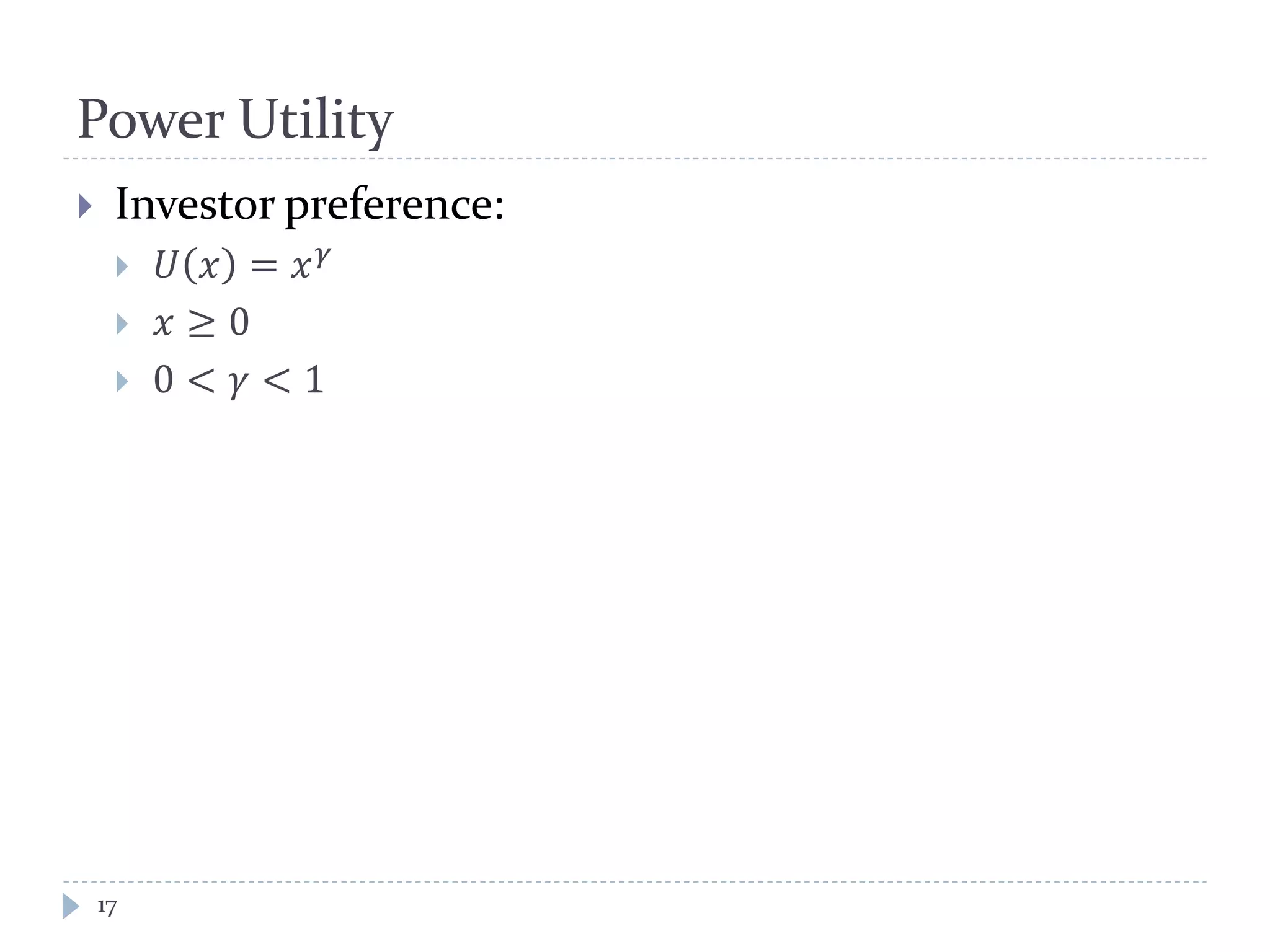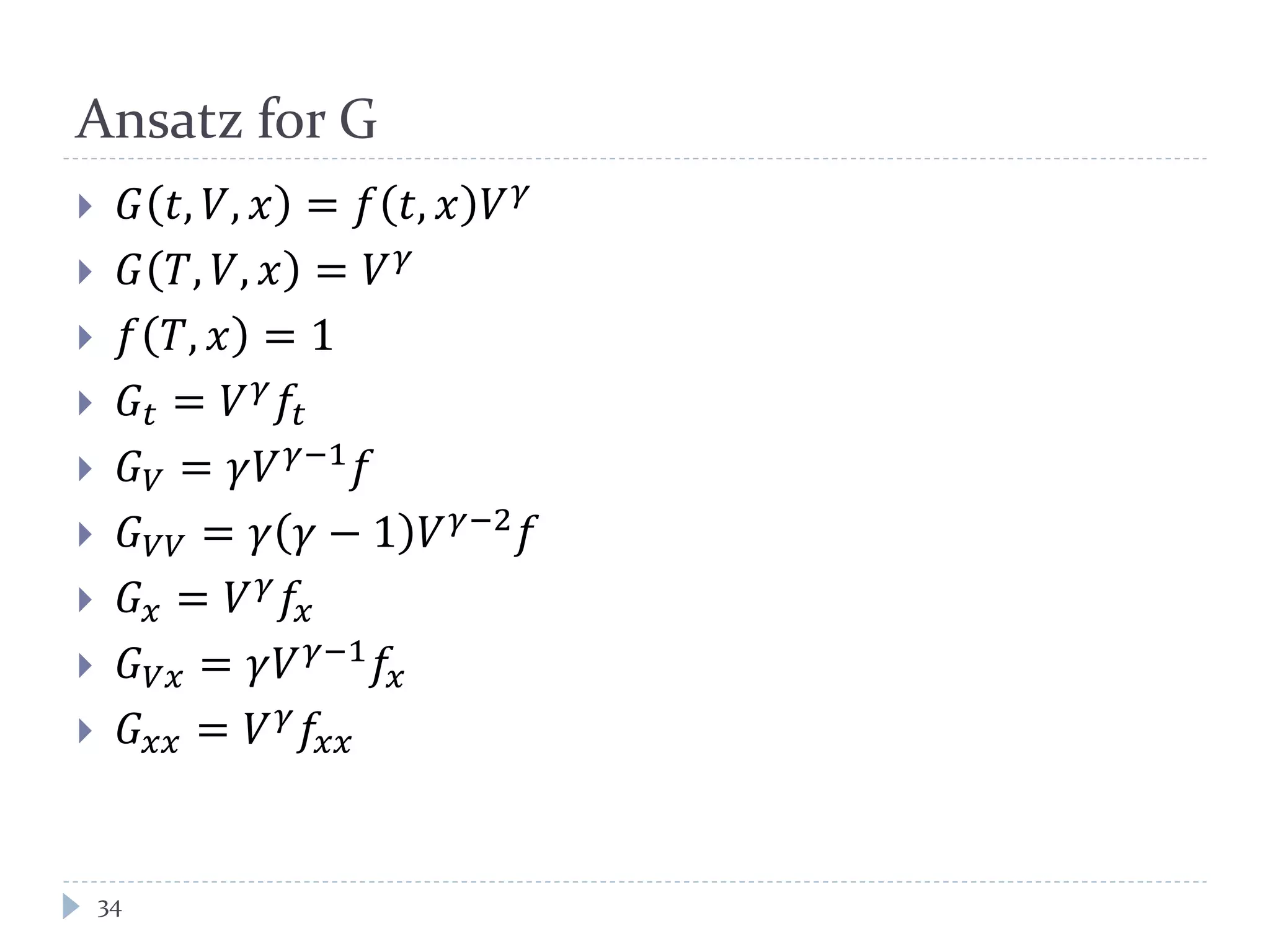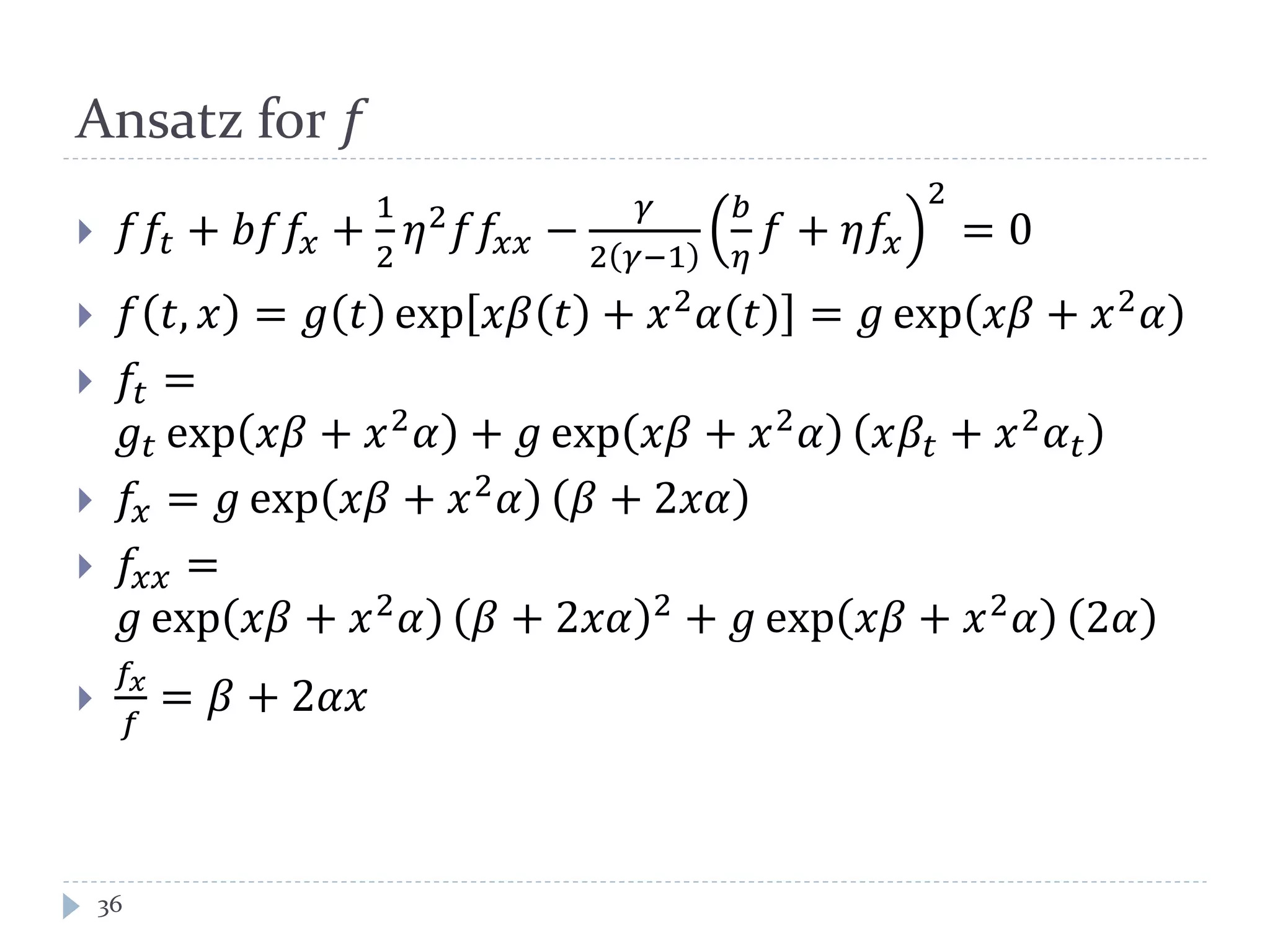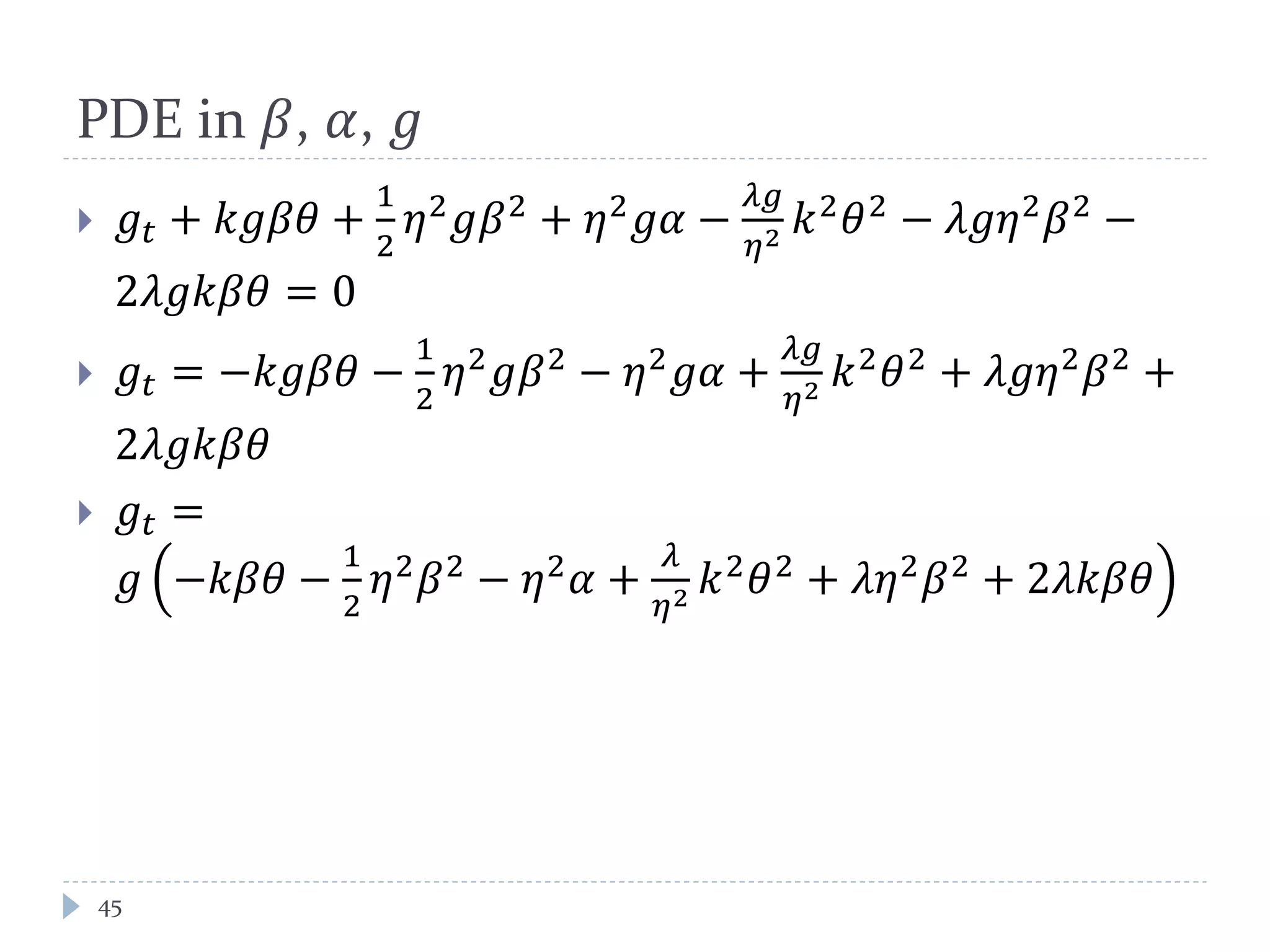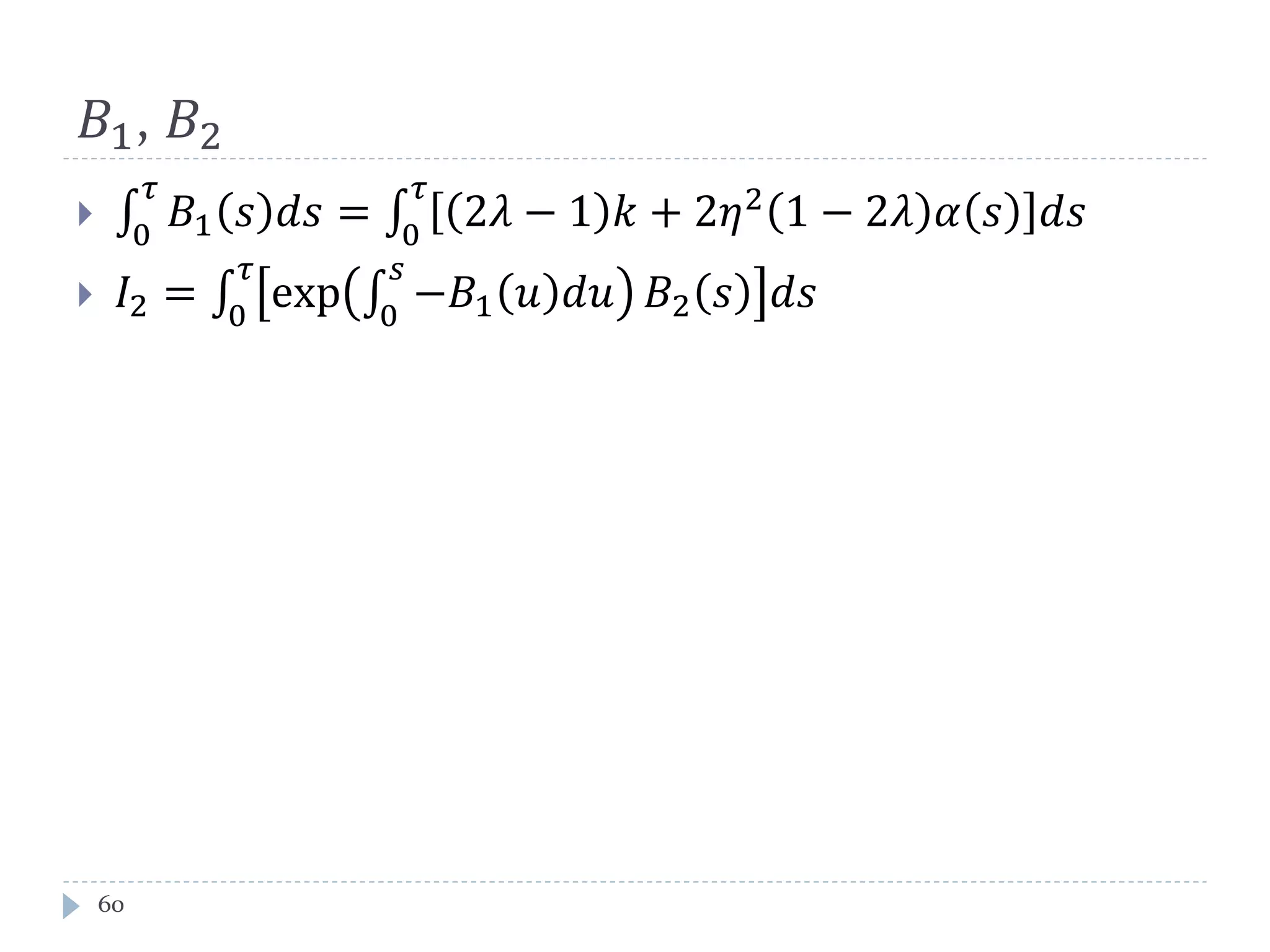This document discusses optimal trading strategies using stochastic control. It provides background on the speaker, Haksun Li, and references related work on optimal pairs trading and trend following rules. It then describes modeling the difference between two asset returns as a mean-reverting Ornstein-Uhlenbeck process. It formulates the optimal trading problem using dynamic programming and stochastic control to maximize expected utility of the trading portfolio value over time.

1. Optimal Trading Strategies
Stochastic Control
Haksun Li
haksun.li@numericalmethod.com
www.numericalmethod.com

2. Speaker Profile
 Dr. Haksun Li
 CEO, Numerical Method Inc.
 (Ex-)Adjunct Professors, Industry Fellow, Advisor,
Consultant with the National University of Singapore,
Nanyang Technological University, Fudan University,
the Hong Kong University of Science and Technology.
 Quantitative Trader/Analyst, BNPP, UBS
 PhD, Computer Sci, University of Michigan Ann Arbor
 M.S., Financial Mathematics, University of Chicago
 B.S., Mathematics, University of Chicago
2

3. References
 Optimal Pairs Trading: A Stochastic Control
Approach. Mudchanatongsuk, S., Primbs, J.A., Wong,
W. Dept. of Manage. Sci. & Eng., Stanford Univ.,
Stanford, CA. 2008.
 Optimal Trend Following Trading Rules. Dai, M.,
Zhang, Q., Zhu Q. J. 2011
3

4. Mean Reversion Trading
4

5. Stochastic Control
 We model the difference between the log-returns of
two assets as an Ornstein-Uhlenbeck process.
 We compute the optimal position to take as a function
of the deviation from the equilibrium.
 This is done by solving the corresponding the
Hamilton-Jacobi-Bellman equation.
5

6. Formulation
 Assume a risk free asset 𝑀𝑡, which satisfies
 𝑑𝑀𝑡 = 𝑟𝑀𝑡 𝑑𝑑
 Assume two assets,𝐴 𝑡 and 𝐵𝑡.
 Assume 𝐵𝑡follows a geometric Brownian motion.
 𝑑𝐵𝑡 = 𝜇𝐵𝑡 𝑑𝑑 + 𝜎𝐵𝑡 𝑑𝑧𝑡
 𝑥 𝑡is the spread between the two assets.
 𝑥𝑡 = log 𝐴 𝑡 − log 𝐵𝑡
6

7. Ornstein-Uhlenbeck Process
 We assume the spread, the basket that we want to
trade, follows a mean-reverting process.
 𝑑𝑥𝑡 = 𝑘 𝜃 − 𝑥𝑡 𝑑𝑑 + 𝜂𝜂𝜔 𝑡
 𝜃 is the long term equilibrium to which the spread
reverts.
 𝑘 is the rate of reversion. It must be positive to ensure
stability around the equilibrium value.
7

8. Instantaneous Correlation
 Let 𝜌 denote the instantaneous correlation coefficient
between 𝑧 and 𝜔.
 𝐸 𝑑𝜔 𝑡 𝑑𝑧𝑡 = 𝜌𝜌𝜌
8

9. Univariate Ito’s Lemma
9
 Assume
 𝑑𝑋𝑡 = 𝜇 𝑡 𝑑𝑑 + 𝜎𝑡 𝑑𝐵𝑡
 𝑓 𝑡, 𝑋𝑡 is twice differentiable of two real variables
 We have
 𝑑𝑑 𝑡, 𝑋𝑡 =
𝜕𝜕
𝜕𝜕
+ 𝜇 𝑡
𝜕𝜕
𝜕𝜕
+
𝜎𝑡
2
2
𝜕2 𝑓
𝜕𝑥2 𝑑𝑑 + 𝜎𝑡
𝜕𝜕
𝜕𝜕
𝑑𝐵𝑡

10. Log example
 For G.B.M., 𝑑𝑋𝑡 = 𝜇𝑋𝑡 𝑑𝑑 + 𝜎𝑋𝑡 𝑑𝑧𝑡, 𝑑 log 𝑋𝑡 =?
 𝑓 𝑥 = log 𝑥

𝜕𝑓
𝜕𝑡
= 0

𝜕𝑓
𝜕𝑥
=
1
𝑥

𝜕2 𝑓
𝜕𝑥2 = −
1
𝑥2
 𝑑 log 𝑋𝑡 = 𝜇𝑋𝑡
1
𝑋𝑡
+
𝜎𝑋𝑡
2
2
−
1
𝑋𝑡
2 𝑑𝑑 + 𝜎𝑋𝑡
1
𝑋𝑡
𝑑𝐵𝑡
 = 𝜇 −
𝜎2
2
𝑑𝑑 + 𝜎𝑑𝐵𝑡
10

11. Multivariate Ito’s Lemma
11
 Assume
 𝑋𝑡 = 𝑋1𝑡, 𝑋2𝑡, ⋯ , 𝑋 𝑛𝑛 is a vector Ito process
 𝑓 𝑥1𝑡, 𝑥2𝑡, ⋯ , 𝑥 𝑛𝑛 is twice differentiable
 We have
 𝑑𝑑 𝑋1𝑡, 𝑋2𝑡, ⋯ , 𝑋 𝑛𝑛
 = ∑
𝜕
𝜕𝑥 𝑖
𝑛
𝑖=1 𝑓 𝑋1𝑡, 𝑋2𝑡, ⋯ , 𝑋 𝑛𝑛 𝑑𝑋𝑖 𝑡
 +
1
2
∑ ∑
𝜕2
𝜕𝑥 𝑖 𝜕𝑥 𝑗
𝑛
𝑗=1
𝑛
𝑖=1 𝑓 𝑋1𝑡, 𝑋2𝑡, ⋯ , 𝑋 𝑛𝑛 𝑑 𝑋𝑖, 𝑋𝑗 𝑡

12. Multivariate Example
 log 𝐴 𝑡 = 𝑥 𝑡 + log 𝐵𝑡
 𝐴 𝑡 = exp 𝑥 𝑡 + log 𝐵𝑡

𝜕𝐴 𝑡
𝜕𝑥 𝑡
= exp 𝑥 𝑡 + log 𝐵𝑡 = 𝐴 𝑡

𝜕𝐴 𝑡
𝜕𝐵𝑡
= exp 𝑥 𝑡 + log 𝐵𝑡
1
𝐵𝑡
=
𝐴 𝑡
𝐵𝑡

𝜕2 𝐴 𝑡
𝜕𝑥 𝑡
2 =
𝜕𝐴 𝑡
𝜕𝑥 𝑡
= 𝐴 𝑡

𝜕2 𝐴 𝑡
𝜕𝐵𝑡
2 =
𝜕
𝜕𝐵𝑡
𝐴 𝑡
𝐵𝑡
= 0

𝜕2 𝐴 𝑡
𝜕𝐵𝑡 𝜕𝑥 𝑡
=
𝜕
𝜕𝐵𝑡
𝜕𝐴 𝑡
𝜕𝑥 𝑡
=
𝜕𝐴 𝑡
𝜕𝐵𝑡
=
𝐴 𝑡
𝐵𝑡
12

13. What is the Dynamic of Asset At?
 𝜕𝐴 𝑡 =
𝜕𝐴 𝑡
𝜕𝜕
𝑑𝑥 𝑡 +
𝜕𝐴 𝑡
𝜕𝐵𝑡
𝑑𝐵𝑡 +
1
2
𝜕2 𝐴 𝑡
𝜕𝑥2 𝑑𝑥 𝑡
2 +
𝜕2 𝐴 𝑡
𝜕𝐵𝑡 𝜕𝑥
𝑑𝑥 𝑡 𝑑𝐵𝑡
 = 𝐴 𝑡 𝑑𝑥 𝑡 +
𝐴 𝑡
𝐵𝑡
𝑑𝐵𝑡 +
1
2
𝐴 𝑡 𝑑𝑥 𝑡
2 +
𝐴 𝑡
𝐵𝑡
𝑑𝑥 𝑡 𝑑𝐵𝑡
 = 𝐴 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + 𝜂𝜂𝜔 𝑡 +
𝐴 𝑡
𝐵𝑡
𝜇𝐵𝑡 𝑑𝑑 + 𝜎𝐵𝑡 𝑑𝑧𝑡 +
1
2
𝐴 𝑡 𝜂2 𝑑𝑑 +
𝐴 𝑡
𝐵𝑡
𝜌𝜂𝜂𝐵𝑡 𝑑𝑑
13

14. Dynamic of Asset At
 𝜕𝐴 𝑡 = 𝐴 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + 𝜂𝜂𝜔 𝑡 + 𝐴 𝑡 𝜇𝑑𝑑 + 𝜎𝑑𝑧𝑡 +
1
2
𝐴 𝑡 𝜂2
𝑑𝑑 + 𝐴 𝑡 𝜌𝜂𝜂𝑑𝑑
 = 𝐴 𝑡 𝑘 𝜃 − 𝑥 𝑡 + 𝜇 +
1
2
𝜂2
+ 𝜌𝜌𝜌 𝑑𝑑 + 𝐴 𝑡 𝜂𝜂𝜔 𝑡 +
𝐴 𝑡 𝜎𝑑𝑧𝑡
 = 𝐴 𝑡 𝜇 + 𝑘 𝜃 − 𝑥 𝑡 +
1
2
𝜂2
+ 𝜌𝜌𝜌 𝑑𝑑 + 𝜎𝑑𝑧𝑡 + 𝜂𝜂𝜔 𝑡
14

15. Notations
 𝑉𝑡: the value of a self-financing pairs trading portfolio
 ℎ 𝑡:the portfolio weight for stock A
 ℎ 𝑡
� = −ℎ 𝑡:the portfolio weight for stock B
15

16. Self-Financing Portfolio Dynamic

𝑑𝑉𝑡
𝑉𝑡
= ℎ 𝑡
𝑑𝐴 𝑡
𝐴 𝑡
+ ℎ 𝑡
� 𝑑𝐵𝑡
𝐵𝑡
+
𝑑𝑀𝑡
𝑀𝑡
 =
ℎ 𝑡 𝜇 + 𝑘 𝜃 − 𝑥 𝑡 +
1
2
𝜂2
+ 𝜌𝜌𝜌 𝑑𝑑 + 𝜎𝑑𝑧𝑡 + 𝜂𝜂𝜔 𝑡 −
ℎ 𝑡 𝜇𝑑𝑑 + 𝜎𝑑𝑧𝑡 + 𝑟𝑟𝑟
 = ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 +
1
2
𝜂2 + 𝜌𝜌𝜌 𝑑𝑑 + 𝜂𝜂𝜔 𝑡 + 𝑟𝑟𝑟
 = ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 +
1
2
𝜂2
+ 𝜌𝜌𝜌 + 𝑟 𝑑𝑑 + ℎ 𝑡 𝜂𝜂𝜔 𝑡
16

17. Power Utility
 Investor preference:
 𝑈 𝑥 = 𝑥 𝛾
 𝑥 ≥ 0
 0 < 𝛾 < 1
17

18. Problem Formulation
 max
ℎ 𝑡
𝐸 𝑉𝑇
𝛾
, s.t.,
 𝑉 0 = 𝑣0, x 0 = 𝑥0
 𝑑𝑥𝑡 = 𝑘 𝜃 − 𝑥𝑡 𝑑𝑑 + 𝜂𝜂𝜔 𝑡
 𝑑𝑉𝑡 = ℎ 𝑡 𝑑𝑥 𝑡 = ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + ℎ 𝑡 𝜂𝜂𝜔 𝑡
 Note that we simplify GBM to BM of 𝑉𝑡, and remove
some constants.
18

19. Dynamic Programming
19
 Consider a stage problem to minimize (or maximize)
the accumulated costs over a system path.
s0
s11
s12
time
t = 0 t = 1
S21
S22
s23
t = 2
3
2
3
5
Cost = 𝑐3 + ∑ 𝑐𝑡
2
𝑡=0
s3
s12
5
4
3
1
5

20. Dynamic Programming Formulation
 State change: 𝑥 𝑘+1 = 𝑓𝑘 𝑥 𝑘, 𝑢 𝑘, 𝜔 𝑘
 𝑘: time
 𝑥 𝑘: state
 𝑢 𝑘: control decision selected at time 𝑘
 𝜔 𝑘: a random noise
 Cost: 𝑔 𝑁 𝑥 𝑁 + ∑ 𝑔 𝑘 𝑥 𝑘, 𝑢 𝑘, 𝜔 𝑘
𝑁−1
𝑘=0
 Objective: minimize (maximize) the expected cost.
 We need to take expectation to account for the noise, 𝜔 𝑘.
20

21. Principle of Optimality
 Let 𝜋∗
= 𝜇0
∗, 𝜇1
∗, ⋯ , 𝜇 𝑁−1
∗ be an optimal policy for
the basic problem, and assume that when using 𝜋∗
, a
give state 𝑥𝑖 occurs at time 𝑖 with positive probability.
Consider the sub-problem whereby we are at 𝑥𝑖 at time
𝑖 and wish to minimize the “cost-to-go” from time 𝑖 to
time 𝑁.
 𝐸 𝑔 𝑁 𝑥 𝑁 + ∑ 𝑔 𝑘 𝑥 𝑘, 𝑢 𝑘, 𝜔 𝑘
𝑁−1
𝑘=𝑖
 Then the truncated policy 𝜇𝑖
∗, 𝜇𝑖+1
∗, ⋯ , 𝜇 𝑁−1
∗ is
optimal for this sub-problem.
21

22. Dynamic Programming Algorithm
 For every initial state 𝑥0, the optimal cost 𝐽∗
𝑥 𝑘 of the
basic problem is equal to 𝐽0 𝑥0 , given by the last step
of the following algorithm, which proceeds backward
in time from period 𝑁 − 1 to period 0:
 𝐽 𝑁 𝑥 𝑁 = 𝑔 𝑁 𝑥 𝑁
 𝐽 𝑘 𝑥 𝑘 = min
𝑢 𝑘
𝐸 𝑔 𝑘 𝑥 𝑘, 𝑢 𝑘, 𝜔 𝑘 + 𝐽 𝑘+1 𝑓𝑘 𝑥 𝑘, 𝑢 𝑘, 𝜔 𝑘
22

23. Value function
 Terminal condition:
 𝐺 𝑇, 𝑉, 𝑥 = 𝑉 𝛾
 DP equation:
 𝐺 𝑡, 𝑉𝑡, 𝑥𝑡 = m𝑎𝑎
ℎ 𝑡
𝐸 𝐺 𝑡 + 𝑑𝑑, 𝑉𝑡+𝑑𝑑, 𝑥𝑡+𝑑𝑑
 𝐺 𝑡, 𝑉𝑡, 𝑥𝑡 = m𝑎𝑎
ℎ 𝑡
𝐸 𝐺 𝑡, 𝑉𝑡, 𝑥𝑡 + Δ𝐺
 By Ito’s lemma:
 Δ𝐺 =
𝐺𝑡 𝑑𝑑 + 𝐺 𝑉 𝑑𝑑 + 𝐺 𝑥 𝑑𝑥 +
1
2
𝐺 𝑉𝑉 𝑑𝑑 2 +
1
2
𝐺 𝑥𝑥 𝑑𝑥 2 +
𝐺 𝑉𝑥 𝑑𝑉 𝑑𝑑
23

24. Hamilton-Jacobi-Bellman Equation
 Cancel 𝐺 𝑡, 𝑉𝑡, 𝑥 𝑡 on both LHS and RHS.
 Divide by time discretization, Δ𝑡.
 Take limit as Δ𝑡 → 0, hence Ito.
 0 = m𝑎𝑎
ℎ 𝑡
𝐸 Δ𝐺
 m𝑎𝑎
ℎ 𝑡
𝐸 𝐺𝑡 𝑑𝑑 + 𝐺 𝑉 𝑑𝑑 + 𝐺 𝑥 𝑑𝑑 +
1
2
𝐺 𝑉𝑉 𝑑𝑑 2 +
1
2
𝐺 𝑥𝑥 𝑑𝑑 2 + 𝐺 𝑉𝑉 𝑑𝑑 𝑑𝑑 =
0
 The optimal portfolio position is ℎ 𝑡
∗
.
24

25. HJB for Our Portfolio Value
 m𝑎𝑎
ℎ 𝑡
𝐸 𝐺𝑡 𝑑𝑑 + 𝐺 𝑉 𝑑𝑑 + 𝐺 𝑥 𝑑𝑑 +
1
2
𝐺 𝑉𝑉 𝑑𝑑 2 +
1
2
𝐺 𝑥𝑥 𝑑𝑑 2 + 𝐺 𝑉𝑉 𝑑𝑑 𝑑𝑑 =
0
 m𝑎𝑎
ℎ 𝑡
𝐸
𝐺𝑡 𝑑𝑑 + 𝐺 𝑉 ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + ℎ 𝑡 𝜂𝜂𝜔 𝑡 + 𝐺 𝑥 𝑑𝑑 +
1
2
𝐺 𝑉𝑉 ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + ℎ 𝑡 𝜂𝜂𝜔 𝑡
2
+
1
2
𝐺 𝑥𝑥 𝑑𝑑 2
+
𝐺 𝑉𝑉 ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + ℎ 𝑡 𝜂𝜂𝜔 𝑡 𝑑𝑑
= 0
 m𝑎𝑎
ℎ 𝑡
𝐸
𝐺𝑡 𝑑𝑑 + 𝐺 𝑉 ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + ℎ 𝑡 𝜂𝜂𝜔 𝑡 +
𝐺 𝑥 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + 𝜂𝜂𝜔 𝑡 +
1
2
𝐺 𝑉𝑉 ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + ℎ 𝑡 𝜂𝜂𝜔 𝑡
2
+
1
2
𝐺 𝑥𝑥 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + 𝜂𝜂𝜔 𝑡
2
+
𝐺 𝑉𝑉 ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + ℎ 𝑡 𝜂𝜂𝜔 𝑡 × 𝑘 𝜃 − 𝑥 𝑡 𝑑𝑑 + 𝜂𝜂𝜔 𝑡
= 0
25

26. Taking Expectation
 All 𝜂𝜂𝜔 𝑡 disapper because of the expectation operator.
 Only the deterministic 𝑑𝑑 terms remain.
 Divide LHR and RHS by 𝑑𝑑.
 m𝑎𝑎
ℎ 𝑡
𝐺𝑡 + 𝐺 𝑉 ℎ 𝑡 𝑘 𝜃 − 𝑥 𝑡 +
𝐺 𝑥 𝑘 𝜃 − 𝑥 𝑡 +
1
2
𝐺 𝑉𝑉 ℎ 𝑡 𝜂 2
+
1
2
𝐺 𝑥𝑥 𝜂2
+𝐺 𝑉𝑉 ℎ 𝑡 𝜂2
= 0
26

27. Dynamic Programming Solution
 Solve for the cost-to-go function, 𝐺𝑡.
 Assume that the optimal policy is ℎ 𝑡
∗
.
27

28. First Order Condition
 Differentiate w.r.t. ℎ 𝑡.
 𝐺 𝑉 𝑘 𝜃 − 𝑥 𝑡 + ℎ 𝑡
∗
𝐺 𝑉𝑉 𝜂2
+ 𝐺 𝑉𝑉 𝜂2
= 0
 ℎ 𝑡
∗
= −
𝐺 𝑉 𝑘 𝜃−𝑥 𝑡 +𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉 𝜂2
 In order to determine the optimal position, ℎ 𝑡
∗
, we
need to solve for 𝐺 to get 𝐺 𝑉, 𝐺 𝑉𝑉, and 𝐺 𝑉𝑉.
28

29. The Partial Differential Equation (1)

𝐺𝑡 −
𝐺 𝑉
𝐺 𝑉 𝑘 𝜃−𝑥 𝑡 +𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉 𝜂2 𝑘 𝜃 − 𝑥 𝑡 +
𝐺 𝑥 𝑘 𝜃 − 𝑥 𝑡 +
1
2
𝐺 𝑉𝑉 𝜂2 𝐺 𝑉 𝑘 𝜃−𝑥 𝑡 +𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉 𝜂2
2
+
1
2
𝐺 𝑥𝑥 𝜂2
−
𝐺 𝑉𝑉 𝜂2 𝐺 𝑉 𝑘 𝜃−𝑥 𝑡 +𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉 𝜂2
= 0
29

30. The Partial Differential Equation (2)

𝐺𝑡 −
𝐺 𝑉 𝑘 𝜃 − 𝑥 𝑡
𝐺 𝑉 𝑘 𝜃−𝑥 𝑡 +𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉 𝜂2 +
𝐺 𝑥 𝑘 𝜃 − 𝑥 𝑡 +
1
2
𝐺 𝑉 𝑘 𝜃−𝑥 𝑡 +𝐺 𝑉𝑉 𝜂2 2
𝐺 𝑉𝑉 𝜂2 +
1
2
𝐺 𝑥𝑥 𝜂2
−
𝐺 𝑉𝑉
𝐺 𝑉 𝑘 𝜃−𝑥 𝑡 +𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉
= 0
30

31. Dis-equilibrium
 Let 𝑏 = 𝑘 𝜃 − 𝑥 𝑡 . Rewrite:
 𝐺𝑡 − 𝐺 𝑉 𝑏
𝐺 𝑉 𝑏+𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉 𝜂2 + 𝐺 𝑥 𝑏 +
1
2
𝐺 𝑉 𝑏+𝐺 𝑉𝑉 𝜂2 2
𝐺 𝑉𝑉 𝜂2 +
1
2
𝐺 𝑥𝑥 𝜂2
−
𝐺 𝑉𝑉
𝐺 𝑉 𝑏+𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉
= 0
 Multiply by 𝐺 𝑉𝑉 𝜂2
.
 𝐺𝑡 𝐺 𝑉𝑉 𝜂2 − 𝐺 𝑉 𝑏 𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2 + 𝐺 𝑥 𝑏𝐺 𝑉𝑉 𝜂2 +
1
2
𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2 2
+
1
2
𝐺 𝑥𝑥 𝐺 𝑉𝑉 𝜂4
−
𝐺 𝑉𝑉 𝜂2 𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2 = 0
31

32. Simplification
 Note that
 −𝐺 𝑉 𝑏 𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2 +
1
2
𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2 2 −
𝐺 𝑉𝑉 𝜂2
𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2
= −
1
2
𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2 2
 The PDE becomes
 𝐺𝑡 𝐺 𝑉𝑉 𝜂2 + 𝐺 𝑥 𝑏𝐺 𝑉𝑉 𝜂2 +
1
2
𝐺 𝑥𝑥 𝐺 𝑉𝑉 𝜂4 −
1
2
𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2 2 = 0
32

33. The Partial Differential Equation (3)
 𝐺𝑡 𝐺 𝑉𝑉 𝜂2 + 𝐺 𝑥 𝑏𝐺 𝑉𝑉 𝜂2 +
1
2
𝐺 𝑥𝑥 𝐺 𝑉𝑉 𝜂4 −
1
2
𝐺 𝑉 𝑏 + 𝐺 𝑉𝑉 𝜂2 2
= 0
33

34. Ansatz for G
 𝐺 𝑡, 𝑉, 𝑥 = 𝑓 𝑡, 𝑥 𝑉 𝛾
 𝐺 𝑇, 𝑉, 𝑥 = 𝑉 𝛾
 𝑓 𝑇, 𝑥 = 1
 𝐺𝑡 = 𝑉 𝛾
𝑓𝑡
 𝐺 𝑉 = 𝛾𝑉 𝛾−1 𝑓
 𝐺 𝑉𝑉 = 𝛾 𝛾 − 1 𝑉 𝛾−2 𝑓
 𝐺 𝑥 = 𝑉 𝛾 𝑓𝑥
 𝐺 𝑉𝑥 = 𝛾𝑉 𝛾−1
𝑓𝑥
 𝐺 𝑥𝑥 = 𝑉 𝛾
𝑓𝑥𝑥
34

35. Another PDE (1)
 𝑉 𝛾
𝑓𝑡 𝛾 𝛾 − 1 𝑉 𝛾−2
𝑓𝜂2
+ 𝑉 𝛾
𝑓𝑥 𝑏𝛾 𝛾 − 1 𝑉 𝛾−2
𝑓𝜂2
+
1
2
𝑉 𝛾
𝑓𝑥𝑥 𝛾 𝛾 − 1 𝑉 𝛾−2
𝑓𝜂4
−
1
2
𝛾𝑉 𝛾−1
𝑓𝑏 + 𝛾𝑉 𝛾−1
𝑓𝑥 𝜂2 2
= 0
 Divide by 𝛾 𝛾 − 1 𝜂2 𝑉2𝛾−2.
 𝑓𝑡 𝑓 + 𝑓𝑥 𝑏𝑓 +
1
2
𝑓𝑥𝑥 𝑓𝜂2
−
𝛾
2 𝛾−1
𝑓
𝑏
𝜂
+ 𝑓𝑥 𝜂
2
= 0
35

36. Ansatz for 𝑓
 𝑓𝑓𝑡 + 𝑏𝑏𝑓𝑥 +
1
2
𝜂2
𝑓𝑓𝑥𝑥 −
𝛾
2 𝛾−1
𝑏
𝜂
𝑓 + 𝜂𝑓𝑥
2
= 0
 𝑓 𝑡, 𝑥 = 𝑔 𝑡 exp 𝑥𝑥 𝑡 + 𝑥2 𝛼 𝑡 = 𝑔 exp 𝑥𝑥 + 𝑥2 𝛼
 𝑓𝑡 =
𝑔𝑡 exp 𝑥𝑥 + 𝑥2
𝛼 + 𝑔 exp 𝑥𝑥 + 𝑥2
𝛼 𝑥𝛽𝑡 + 𝑥2
𝛼 𝑡
 𝑓𝑥 = 𝑔 exp 𝑥𝑥 + 𝑥2
𝛼 𝛽 + 2𝑥𝑥
 𝑓𝑥𝑥 =
𝑔 exp 𝑥𝑥 + 𝑥2
𝛼 𝛽 + 2𝑥𝑥 2
+ 𝑔 exp 𝑥𝑥 + 𝑥2
𝛼 2𝛼

𝑓𝑥
𝑓
= 𝛽 + 2𝛼𝛼
36

37. Boundary Conditions
 𝑓 𝑇, 𝑥 = 𝑔 𝑇 exp 𝑥𝑥 𝑇 + 𝑥2 𝛼 𝑇 = 1
 𝑔 𝑇 = 1
 𝛼 𝑇 = 0
 𝛽 𝑇 = 0
37

38. Yet Another PDE (1)
 𝑔 exp 𝑥𝑥 + 𝑥2 𝛼 𝑔𝑡 exp 𝑥𝑥 + 𝑥2 𝛼 + 𝑔 exp 𝑥𝑥 + 𝑥2 𝛼 𝑥𝛽𝑡 + 𝑥2 𝛼 𝑡 +
𝑏𝑏 exp 𝑥𝑥 + 𝑥2
𝛼 𝑔 exp 𝑥𝑥 + 𝑥2
𝛼 𝛽 + 2𝑥𝑥 +
1
2
𝜂2 𝑔 exp 𝑥𝑥 + 𝑥2 𝛼 𝑔 exp 𝑥𝑥 + 𝑥2 𝛼 𝛽 + 2𝑥𝑥 2 + 𝑔 exp 𝑥𝑥 + 𝑥2 𝛼 2𝛼 −
𝛾
2 𝛾−1
𝑏
𝜂
𝑔 exp 𝑥𝑥 + 𝑥2 𝛼 + 𝜂𝜂 exp 𝑥𝑥 + 𝑥2 𝛼 𝛽 + 2𝑥𝑥
2
= 0
 Divide by g exp 𝑥𝑥 + 𝑥2
𝛼 exp 𝑥𝑥 + 𝑥2
𝛼 .
 𝑔𝑡 + 𝑔 𝑥𝛽𝑡 + 𝑥2
𝛼 𝑡 + 𝑏𝑏 𝛽 + 2𝑥𝑥 +
1
2
𝜂2
𝑔 𝛽 + 2𝑥𝑥 2
+ 𝑔 2𝛼 −
𝛾
2 𝛾−1
𝑔
𝑏
𝜂
+ 𝜂 𝛽 + 2𝑥𝑥
2
= 0
 𝑔𝑡 + 𝑔 𝑥𝛽𝑡 + 𝑥2
𝛼 𝑡 + 𝑏𝑏 𝛽 + 2𝑥𝑥 +
1
2
𝜂2
𝑔 𝛽 + 2𝑥𝑥 2
+ 𝜂2
𝑔𝑔 −
𝛾
2 𝛾−1
𝑔
𝑏
𝜂
+ 𝜂 𝛽 + 2𝑥𝑥
2
= 0
38

39. Yet Another PDE (2)
 𝜆 =
𝛾
2 𝛾−1
 𝑔𝑡 + 𝑔 𝑥𝛽𝑡 + 𝑥2 𝛼 𝑡 + 𝑏𝑏 𝛽 + 2𝑥𝑥 +
1
2
𝜂2 𝑔 𝛽 + 2𝑥𝑥 2 + 𝜂2 𝑔𝑔 − 𝜆𝑔
𝑏
𝜂
+ 𝜂 𝛽 + 2𝑥𝑥
2
= 0
39

40. Expansion in 𝑥
 𝑔𝑡 + 𝑔𝑔𝛽𝑡 + 𝑔𝑥2
𝛼 𝑡 + 𝑏𝑏𝛽 + 2𝑥𝑥𝑏𝑏 +
1
2
𝜂2
𝑔 𝛽2
+ 4𝑥2
𝛼2
+ 4𝑥𝑥𝑥 + 𝜂2
𝑔𝑔 −
𝜆𝑔
𝑏2
𝜂2 + 𝜂2
𝛽2
+ 4𝜂2
𝑥2
𝛼2
+ 2𝑏𝑏 + 4𝑏𝑏𝑏 + 4𝜂2
𝑥𝑥𝑥 = 0
 𝑔𝑡 + 𝑔𝑔𝛽𝑡 + 𝑔𝑥2
𝛼 𝑡 + 𝑘 𝜃 − 𝑥 𝑔𝛽 + 2𝑥𝑥𝑘 𝜃 − 𝑥 𝑔 +
1
2
𝜂2 𝑔 𝛽2 + 4𝑥2 𝛼2 + 4𝑥𝑥𝑥 + 𝜂2 𝑔𝑔 −
𝜆𝑔
𝑘2 𝜃−𝑥 2
𝜂2 + 𝜂2
𝛽2
+ 4𝜂2
𝑥2
𝛼2
+ 2𝑘 𝜃 − 𝑥 𝛽 + 4𝑘 𝜃 − 𝑥 𝑥𝑥 + 4𝜂2
𝑥𝑥𝑥 = 0
 𝑔𝑡 + 𝑔𝑔𝛽𝑡 + 𝑔𝑥2
𝛼 𝑡 + 𝑘𝑘𝛽𝛽 − 𝑘𝑘𝛽𝑥 + 2𝑥𝑥𝑘𝑘𝜃 − 2𝛼𝑘𝑘𝑥2
+
1
2
𝜂2
𝑔𝛽2
+
2𝜂2
𝑔𝑥2
𝛼2
+ 2𝜂2
𝑔𝑔𝑔𝑔 + 𝜂2
𝑔𝑔 −
𝜆𝑔
𝜂2 𝑘2
𝜃2
+ 2
𝜆𝑔
𝜂2 𝑘2
𝜃𝑥 −
𝜆𝑔
𝜂2 𝑘2
𝑥2
− 𝜆𝑔𝜂2
𝛽2
−
4𝜆𝑔𝜂2
𝑥2
𝛼2
− 2𝜆𝑔𝑔𝛽𝛽 + 2𝜆𝑔𝑔𝛽𝑥 − 4𝜆𝑔𝑔𝜃𝜃𝜃 + 4𝜆𝑔𝑔𝑥2
𝛼 − 4𝜆𝑔𝜂2
𝑥𝑥𝑥 = 0
40

41. Grouping in 𝑥
 𝑔𝑡 + 𝑘𝑘𝛽𝛽 +
1
2
𝜂2
𝑔𝛽2
+ 𝜂2
𝑔𝑔 −
𝜆𝑔
𝜂2 𝑘2
𝜃2
− 𝜆𝑔𝜂2
𝛽2
− 2𝜆𝑔𝑔𝛽𝛽 +
𝑔𝛽𝑡 − 𝑘𝑘𝛽 + 2𝛼𝑘𝑘𝜃 + 2𝜂2
𝑔𝑔𝑔 + 2
𝜆𝑔
𝜂2 𝑘2
𝜃 + 2𝜆𝑔𝑔𝛽 − 4𝜆𝑔𝑔𝜃𝜃 − 4𝜆𝑔𝜂2
𝛼𝛼 𝑥 +
𝑔𝛼 𝑡 − 2𝛼𝑘𝑘 + 2𝜂2
𝑔𝛼2
−
𝜆𝑔
𝜂2 𝑘2
− 4𝜆𝑔𝜂2
𝛼2
+ 4𝜆𝑔𝑔𝛼 𝑥2
= 0
41

42. The Three PDE’s (1)
 𝑔𝛼 𝑡 − 2𝛼𝑘𝑘 + 2𝜂2
𝑔𝛼2
−
𝜆𝑔
𝜂2 𝑘2
− 4𝜆𝑔𝜂2
𝛼2
+ 4𝜆𝑔𝑔𝛼 =
0
 𝑔𝛽𝑡 − 𝑘𝑘𝛽 + 2𝛼𝑘𝑘𝜃 + 2𝜂2 𝑔𝑔𝑔 + 2
𝜆𝑔
𝜂2 𝑘2 𝜃 + 2𝜆𝑔𝑔𝛽 −
4𝜆𝑔𝑔𝜃𝜃 − 4𝜆𝑔𝜂2
𝛼𝛼 = 0
 𝑔𝑡 + 𝑘𝑘𝛽𝛽 +
1
2
𝜂2
𝑔𝛽2
+ 𝜂2
𝑔𝑔 −
𝜆𝑔
𝜂2 𝑘2
𝜃2
− 𝜆𝑔𝜂2
𝛽2
−
2𝜆𝑔𝑔𝛽𝛽 = 0
42

43. PDE in 𝛼
 𝛼 𝑡 + 2𝜂2
− 4𝜆𝜆2
𝛼2
+ 4𝜆𝑘 − 2𝑘 𝛼 −
𝜆
𝜂2 𝑘2
= 0
 𝛼 𝑡 =
𝜆
𝜂2 𝑘2
+ 2𝑘 1 − 2𝜆 𝛼 + 2𝜂2
2𝜆 − 1 𝛼2
43

44. PDE in 𝛽, 𝛼
 𝛽𝑡 − 𝑘𝛽 + 2𝜂2
𝛼𝛼 + 2𝜆𝑘𝛽 − 4𝜆𝜆2
𝛼𝛼 − 4𝜆𝑘𝜃𝜃 +
2
𝜆
𝜂2 𝑘2
𝜃 + 2𝛼𝑘𝜃 = 0
 𝛽𝑡 =
𝑘 − 2𝜂2 𝛼 − 2𝜆𝑘 + 4𝜆𝜆2 𝛼 𝛽 +
4𝜆𝑘𝜃𝜃 − 2
𝜆
𝜂2 𝑘2 𝜃 − 2𝛼𝑘𝜃
44

45. PDE in 𝛽, 𝛼, 𝑔
 𝑔𝑡 + 𝑘𝑘𝛽𝛽 +
1
2
𝜂2
𝑔𝛽2
+ 𝜂2
𝑔𝑔 −
𝜆𝑔
𝜂2 𝑘2
𝜃2
− 𝜆𝑔𝜂2
𝛽2
−
2𝜆𝑔𝑔𝛽𝛽 = 0
 𝑔𝑡 = −𝑘𝑘𝛽𝛽 −
1
2
𝜂2 𝑔𝛽2 − 𝜂2 𝑔𝑔 +
𝜆𝑔
𝜂2 𝑘2 𝜃2 + 𝜆𝑔𝜂2 𝛽2 +
2𝜆𝑔𝑔𝛽𝛽
 𝑔𝑡 =
𝑔 −𝑘𝛽𝛽 −
1
2
𝜂2
𝛽2
− 𝜂2
𝛼 +
𝜆
𝜂2 𝑘2
𝜃2
+ 𝜆𝜆2
𝛽2
+ 2𝜆𝑘𝛽𝛽
45

46. Riccati Equation
 A Riccati equation is any ordinary differential equation
that is quadratic in the unknown function.
 𝛼 𝑡 =
𝜆
𝜂2 𝑘2
+ 2𝑘 1 − 2𝜆 𝛼 + 2𝜂2
2𝜆 − 1 𝛼2
 𝛼 𝑡 = 𝐴0 + 𝐴1 𝛼 + 𝐴2 𝛼2
46

47. Solving a Riccati Equation by Integration
 Suppose a particular solution, 𝛼1, can be found.
 𝛼 = 𝛼1 +
1
𝑧
is the general solution, subject to some
boundary condition.
47

48. Particular Solution
 Either 𝛼1 or 𝛼2 is a particular solution to the ODE.
This can be verified by mere substitution.
 𝛼1,2 =
−𝐴1± 𝐴1
2
−4𝐴2 𝐴0
2𝐴2
48

49. 𝑧 Substitution
 Suppose 𝛼 = 𝛼1 +
1
𝑧
.

1
𝑧
̇
= 𝐴0 + 𝐴1 𝛼1 +
1
𝑧
+ 𝐴2 𝛼1 +
1
𝑧
2
 = 𝐴0 + 𝐴1 𝛼1 + 𝐴1
1
𝑧
+ 𝐴2 𝛼1
2
+ 𝐴2
1
𝑧2 + 2𝐴2
𝛼1
𝑧
 = 𝐴0 + 𝐴1 𝛼1 + 𝐴1
1
𝑧
+ 𝐴2 𝛼1
2
+ 𝐴2
1
𝑧2 + 2𝐴2
𝛼1
𝑧
 = 𝐴0 + 𝐴1 𝛼1 + 𝐴2 𝛼1
2
+
𝐴1+2𝛼1 𝐴2
𝑧
+
𝐴2
𝑧2
goes to 0 by the definition of 𝛼1
49

50. Solving 𝑧

1
𝑧
̇
=
𝐴1+2𝛼1 𝐴2
𝑧
+
𝐴2
𝑧2
 −
1
𝑧2 𝑧̇ =
𝐴1+2𝛼1 𝐴2
𝑧
+
𝐴2
𝑧2
 1st order linear ODE
 𝑧̇ + 𝐴1 + 2𝛼1 𝐴2 𝑧 = −𝐴2
 𝑧 𝑡 =
−𝐴2
𝐴1+2𝛼1 𝐴2
+ 𝐶exp − 𝐴1 + 2𝛼1 𝐴2 𝑡
50

51. Solving for 𝛼
 𝛼 = 𝛼1 +
1
−𝐴2
𝐴1+2𝛼1 𝐴2
+𝐶exp− 𝐴1+2𝛼1 𝐴2 𝑡
 boundary condition:
 𝛼 𝑇 = 0
 𝛼1 +
1
−𝐴2
𝐴1+2𝛼1 𝐴2
+𝐶exp− 𝐴1+2𝛼1 𝐴2 𝑇
= 0
 𝐶exp − 𝐴1 + 2𝛼1 𝐴2 𝑇 = −
1
𝛼1
+
𝐴2
𝐴1+2𝛼1 𝐴2
 𝐶 = exp 𝐴1 + 2𝛼1 𝐴2 𝑇
𝐴2
𝐴1+2𝛼1 𝐴2
−
1
𝛼1
51

52. 𝛼 Solution (1)
 𝛼 = 𝛼1 +
1
−𝐴2
𝐴1+2𝛼1 𝐴2
+𝐶exp− 𝐴1+2𝛼1 𝐴2 𝑡
 =
𝛼1 +
1
−𝐴2
𝐴1+2𝛼1 𝐴2
+exp 𝐴1+2𝛼1 𝐴2 𝑇
𝐴2
𝐴1+2𝛼1 𝐴2
−
1
𝛼1
exp − 𝐴1+2𝛼1 𝐴2 𝑡
 = 𝛼1 +
1
−𝐴2
𝐴1+2𝛼1 𝐴2
+exp 𝐴1+2𝛼1 𝐴2 𝑇−𝑡
𝐴2
𝐴1+2𝛼1 𝐴2
−
1
𝛼1
 = 𝛼1 +
𝛼1 𝐴1+2𝛼1 𝐴2
−𝛼1 𝐴2+exp 𝐴1+2𝛼1 𝐴2 𝑇−𝑡 𝛼1 𝐴2−𝐴1−2𝛼1 𝐴2
52

53. 𝛼 Solution (2)
 𝛼 = 𝛼1 +
𝛼1 𝐴1+2𝛼1 𝐴2
−𝛼1 𝐴2+exp 𝐴1+2𝛼1 𝐴2 𝑇−𝑡 −𝐴1−𝛼1 𝐴2
 = 𝛼1 1 −
𝐴1+2𝛼1 𝐴2
𝐴2+exp 𝐴1+2𝛼1 𝐴2 𝑇−𝑡
𝐴1
𝛼1
+𝐴2
 = 𝛼1 1 −
𝐴1
𝐴2
+2𝛼1
1+
𝐴1
𝛼1 𝐴2
+1 exp 𝐴1+2𝛼1 𝐴2 𝑇−𝑡
53

54. 𝛼 Solution (3)
 𝛼 𝑡 =
𝑘
2𝜂2 1 − 1 − 𝛾 +
2 1−𝛾
1+ 1−
2
1− 1−𝛾
exp 2𝑘
1−𝛾
𝑇−𝑡
54

55. Solving 𝛽
 𝛽𝑡 = 𝑘 − 2𝜂2
𝛼 − 2𝜆𝑘 + 4𝜆𝜆2
𝛼 𝛽 + 4𝜆𝑘𝜃𝜃 − 2
𝜆
𝜂2 𝑘2
𝜃 − 2𝛼𝑘𝜃
 Let 𝜏 = 𝑇 − 𝑡
 𝛽̂ 𝜏 = 𝛽 𝑇 − 𝑡
 𝛽̂ 𝜏 𝜏 = −𝛽𝑡 𝜏
 −𝛽̂ 𝜏 𝜏 = 𝛽𝑡 𝜏 = 𝑘 − 2𝜂2
𝛼 𝜏 − 2𝜆𝑘 + 4𝜆𝜆2
𝛼 𝜏 𝛽 𝜏 +
4𝜆𝑘𝜃𝜃 𝜏 − 2
𝜆
𝜂2 𝑘2 𝜃 − 2𝛼 𝜏 𝑘𝜃
 𝛽̂ 𝜏 𝜏 =
−𝑘 + 2𝜂2
𝛼� + 2𝜆𝑘 − 4𝜆𝜆2
𝛼� 𝛽̂ + −4𝜆𝑘𝜃𝛼� + 2
𝜆
𝜂2 𝑘2
𝜃 + 2𝛼�𝑘𝜃
 𝛽̂ 𝜏 𝜏 =
2𝜆 − 1 𝑘 + 2𝜂2
𝛼� 1 − 2𝜆 𝛽̂ + 2𝛼�𝑘𝜃 1 − 2𝜆 + 2
𝜆
𝜂2 𝑘2
𝜃
55

56. First Order Non-Constant Coefficients
 𝛽̂ 𝜏 = 𝐵1 𝛽̂ + 𝐵2
 𝐵1 𝜏 = 2𝜆 − 1 𝑘 + 2𝜂2
𝛼� 1 − 2𝜆
 𝐵2 𝜏 = 2𝛼�𝑘𝜃 1 − 2𝜆 + 2
𝜆
𝜂2 𝑘2 𝜃
56

57. Integrating Factor (1)
 𝛽̂ 𝜏 − 𝐵1 𝛽̂ = 𝐵2
 We try to find an integrating factor 𝜇 = 𝜇 𝜏 s.t.

𝑑
𝑑𝜏
𝜇𝛽̂ = 𝜇
𝑑𝛽�
𝑑𝜏
+ 𝛽̂ 𝑑𝜇
𝑑𝜏
= 𝜇𝐵2
 Divide LHS and RHS by 𝜇𝛽̂.

1
𝛽�
𝑑𝛽�
𝑑𝑑
+
1
𝜇
𝑑𝜇
𝑑𝜏
=
𝐵2
𝛽�
 By comparison,
 −𝐵1 =
1
𝜇
𝑑𝜇
𝑑𝜏
57

58. Integrating Factor (2)
 ∫ −𝐵1 𝑑𝜏 = ∫
𝑑𝜇
𝜇
= log 𝜇 + 𝐶
 𝜇 = exp ∫ −𝐵1 𝑑𝜏
 𝜇𝛽̂ = ∫ 𝜇𝐵2 𝑑𝜏 + 𝐶
 𝛽̂ =
∫ 𝜇𝐵2 𝑑𝜏+𝐶
𝜇
 𝛽̂ =
∫ exp ∫ −𝐵1 𝑑𝑢 𝐵2 𝑑𝜏+𝐶
exp ∫ −𝐵1 𝑑𝜏
58

59. 𝛽̂ Solution
 𝛽̂ =
∫ exp ∫ −𝐵1 𝑢 𝑑𝑑
𝜏
0
𝐵2 𝑠 𝑑𝑠
𝜏
0
exp ∫ −𝐵1 𝑢 𝑑𝑢
𝜏
0
+ 𝐶
 𝛽̂ 𝜏 =
exp ∫ 𝐵1 𝑢 𝑑𝑑
𝜏
0 ∫ exp ∫ −𝐵1 𝑢 𝑑𝑑
𝑠
0
𝐵2 𝑠 𝑑𝑑
𝜏
0
+ 𝐶
59

60. 𝐵1, 𝐵2
 ∫ 𝐵1 𝑠 𝑑𝑑
𝜏
0
= ∫ 2𝜆 − 1 𝑘 + 2𝜂2
1 − 2𝜆 𝛼 𝑠 𝑑𝑑
𝜏
0
 𝐼2 = ∫ exp ∫ −𝐵1 𝑢 𝑑𝑑
𝑠
0
𝐵2 𝑠 𝑑𝑑
𝜏
0
60

61. 𝛽 Solution
 𝛽 𝑡 =
𝑘𝜃
𝜂2 1 + 1 − 𝛾
exp 2𝑘
1−𝛾
𝑇−𝑡 −1
1+ 1−
2
1− 1−𝛾
exp 2𝑘
1−𝛾
𝑇−𝑡
61

62. Solving 𝑔
 𝑔𝑡 =
𝑔 −𝑘𝛽𝛽 −
1
2
𝜂2
𝛽2
− 𝜂2
𝛼 +
𝜆
𝜂2 𝑘2
𝜃2
+ 𝜆𝜆2
𝛽2
+ 2𝜆𝑘𝛽𝛽
 With𝛼 and 𝛽 solved, we are now ready to solve 𝑔𝑡.

𝑔 𝑡
𝑔
= 𝐺 𝑡

𝑑
𝑑𝑠
log 𝑔𝑡 =
𝑔 𝑡
𝑔
= 𝐺
 log 𝑔𝑡 = ∫ 𝐺𝐺𝐺 + 𝐶
 𝑔𝑡 = 𝐶exp ∫ 𝐺𝑑𝑑 = exp − ∫ 𝐺𝐺𝐺
𝑇
0
exp ∫ 𝐺𝐺𝐺
𝑡
0
 𝑔𝑡 = exp − ∫ 𝐺𝐺𝐺
𝑇
𝑡
62

63. Computing the Optimal Position
 ℎ 𝑡 ∗ = −
𝐺 𝑉 𝑘 𝜃−𝑥 𝑡 +𝐺 𝑉𝑉 𝜂2
𝐺 𝑉𝑉 𝜂2
 = −
𝛾𝑉 𝛾−1 𝑓 𝑘 𝜃−𝑥 𝑡 +𝛾𝑉 𝛾−1 𝑓𝑥 𝜂2
𝛾 𝛾−1 𝑉 𝛾−2 𝑓𝜂2
 = −
𝑉𝑓 𝑘 𝜃−𝑥 𝑡 +𝑉𝑓𝑥 𝜂2
𝛾−1 𝑓𝜂2
 = −
𝑉
𝛾−1 𝜂2
𝑓 𝑘 𝜃−𝑥 𝑡 +𝑓𝑥 𝜂2
𝑓
 = −
𝑉
𝛾−1 𝜂2 𝑘 𝜃 − 𝑥𝑡 +
𝑓𝑥
𝑓
𝜂2
 =
𝑉
1−𝛾 𝜂2 𝑘 𝜃 − 𝑥𝑡 + 𝜂2 𝛽 + 2𝛼𝛼
 =
𝑉
1−𝛾
−
𝑘
𝜂2 𝑥𝑡 − 𝜃 + 2𝛼𝛼 + 𝛽
63

64. The Optimal Position
 ℎ 𝑡 ∗
=
𝑉𝑡
1−𝛾
−
𝑘
𝜂2 𝑥 𝑡 − 𝜃 + 2𝛼 𝑡 𝑥 𝑡 + 𝛽 𝑡
 ℎ 𝑡 ∗~ −
𝑘
𝜂2 𝑥 𝑡 − 𝜃
64

65. P&L for Simulated Data
 The portfolio increases from $1000 to $4625 in one year.
65

66. Parameter Estimation
 Can be done using Maximum Likelihood.
 Evaluation of parameter sensitivity can be done by
Monte Carlo simulation.
 In real trading, it is better to be conservative about the
parameters.
 Better underestimate the mean-reverting speed
 Better overestimate the noise
 To account for parameter regime changes, we can use:
 a hidden Markov chain model
 moving calibration window
66

67. Trend Following Trading
67

68. Two-State Markov Model
68
 𝑑𝑆𝑟 = 𝑆𝑟 𝜇 𝛼 𝑟 𝑑𝑑 + 𝜎𝜎𝐵𝑟
𝛼 𝑟 = 0
DOWN
TREND
𝛼 𝑟 = 1
UP TREND
q p
1-q
1-p

69. Buying and Selling Decisions
69
 𝑡 ≤ 𝜏1
0
≤ 𝜈1
0
≤ 𝜏2
0
≤ 𝜈2
0
≤ ⋯ ≤ 𝜏 𝑛
0 ≤ 𝜈 𝑛
0 ≤ ⋯ ≤ 𝑇

70. Optimal Trend Following Strategy
70

71. Trading SSE 2001 – 2011
71