Empowering Fourier-based Pricing Methods for Efficient Valuation of High-Dimensional Derivatives

Empowering Fourier-based Pricing Methods for
Efficient Valuation of High-Dimensional Derivatives
Chiheb Ben Hammouda
based on joint works with
Christian Bayer Michael Samet Antonis
Papapantoleon
Raúl Tempone
Center for Uncertainty
Quantification
Cente
Quan
Center for Uncertainty Quantification Logo Lock
22nd Winter School on Mathematical Finance
Soesterberg, 20-22 January 2025

Related Works and Resources to the Talk
1 C. Ben Hammouda et al. “Optimal Damping with Hierarchical Adaptive
Quadrature for Efficient Fourier Pricing of Multi-Asset Options in Lévy
Models”. In: Journal of Computational Finance 27.3 (2023), pp. 43–86.
2 C. Ben Hammouda et al. “Quasi-Monte Carlo for Efficient Fourier Pricing
of Multi-Asset Options”. In: arXiv preprint arXiv:2403.02832 (2024).
3 Python Resources and Notebooks: Git repository:
Quasi-Monte-Carlo-for-Efficient-Fourier-Pricing-of-Multi-Asset-Options
1/55

Outline
1 Motivation and Framework
2 Uncovering the Available Hidden Regularity: Mapping the Problem
to the Fourier Space
3 Parametric Smoothing: Near-Optimal Damping Rule
4 Addressing the Curse of Dimension: Quasi-Monte Carlo with
Effective Domain Transformation
5 Conclusions

5 Conclusions
2/55

Framework and Problem Setting
Task: Compute efficiently (up to a discount factor)
E[P(X(T)) ∣ X(0) = x0] = ∫
Rd
P(x) ρXT ∣x0
(x) dx
▸ P ∶ Rd
→ R: payoff function
▸ {Xt ∈ Rd
∶ t ≥ 0}: stochastic processes representing the log-prices of
the underlying assets (resp. risk factors) at time t, defined on a
continuous-time probability space (Ω,F,Q), with Q is the
risk-neutral measure.
Applications in Mathematical Finance: Computing the value
of derivatives (resp. risk measures) depending on multiple assets
(resp. risk factors) and their sensitivities (Greeks).
Features of the problem
P(⋅) is non-smooth.
The dimension d is large.
The pdf, ρXT
, is not known explicitly or expensive to
sample from.
3/55

Task ((Multi-Asset) Option Pricing and Beyond): Compute efficiently (up to a
discount factor)
E[P(X(T)) ∣ X(0) = x0] = ∫
Rd
P(x) ρXT ∣x0
(x) dx
Setting: Payoff Function
P(⋅): payoff function (typically non-smooth), e.g., (K: the strike price)
▸ Basket put: P(x) = max(K − ∑
d
i=1 ciexi
,0), s.t. ci > 0,∑
d
i=1 ci = 1;
▸ Rainbow (E.g., Call on min): P(x) = max(min(ex1
,...,exd
) − K,0)
▸ Cash-or-nothing (CON) put : P(x) = ∏
d
i=1 1[0,Ki](exi
).
x1
4
2
0
2
4
x
2
4
2
0
2
4
P(x
1
,
x
2
)
0.0
0.2
0.4
0.6
0.8
(a) Basket put
x1
0.0
0.2
0.4
0.6
0.8
1.0
x
2
0.0
0.2
0.4
0.6
0.8
1.0
P
(
x
1
,
x
2
)
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
(b) Call on min
x1
0
1
2
3
4
5
6
7
x
2
0
1
2
3
4
5
6
7
P(x
1
,
x
2
)
0.0
0.2
0.4
0.6
0.8
1.0
(c) Cash-or-nothing
Figure 1.1: Payoff functions illustration

Task ((Multi-Asset) Option Pricing and Beyond): Compute efficiently (up to
a discount factor)
E[P(X(T)) ∣ X(0) = x0] = ∫
Rd
P(x) ρXT ∣x0
(x) dx
Setting: Asset Price Model
XT is a d-dimensional (d ≥ 1) vector of log-asset prices at time T,
following a multivariate stochastic model:
▸ Characteristic function, ΦXT
(⋅) ∶= EρXT
[ei⟨⋅,XT ⟩
],
can be known (semi-)analytically or approximated numerically,
e.g,.
☀ Lévy models (Cont et al. 2003): Characteristic function obtained
via Lévy–Khintchine representation.
☀ Affine processes (Duffie et al. 2003): Characteristic function
obtained via Ricatti Equations.
▸ The pdf, ρXT
, is
☀ not known explicitly (e.g. α-stable Lévy processes
(0 < α ≤ 2, α ≠ {1, 1
2
, 2}) (Eberlein 2009)), or
☀ expensive to sample from (e.g. non-Markovian models such
as rough Heston (El Euch et al. 2019)).
5/55

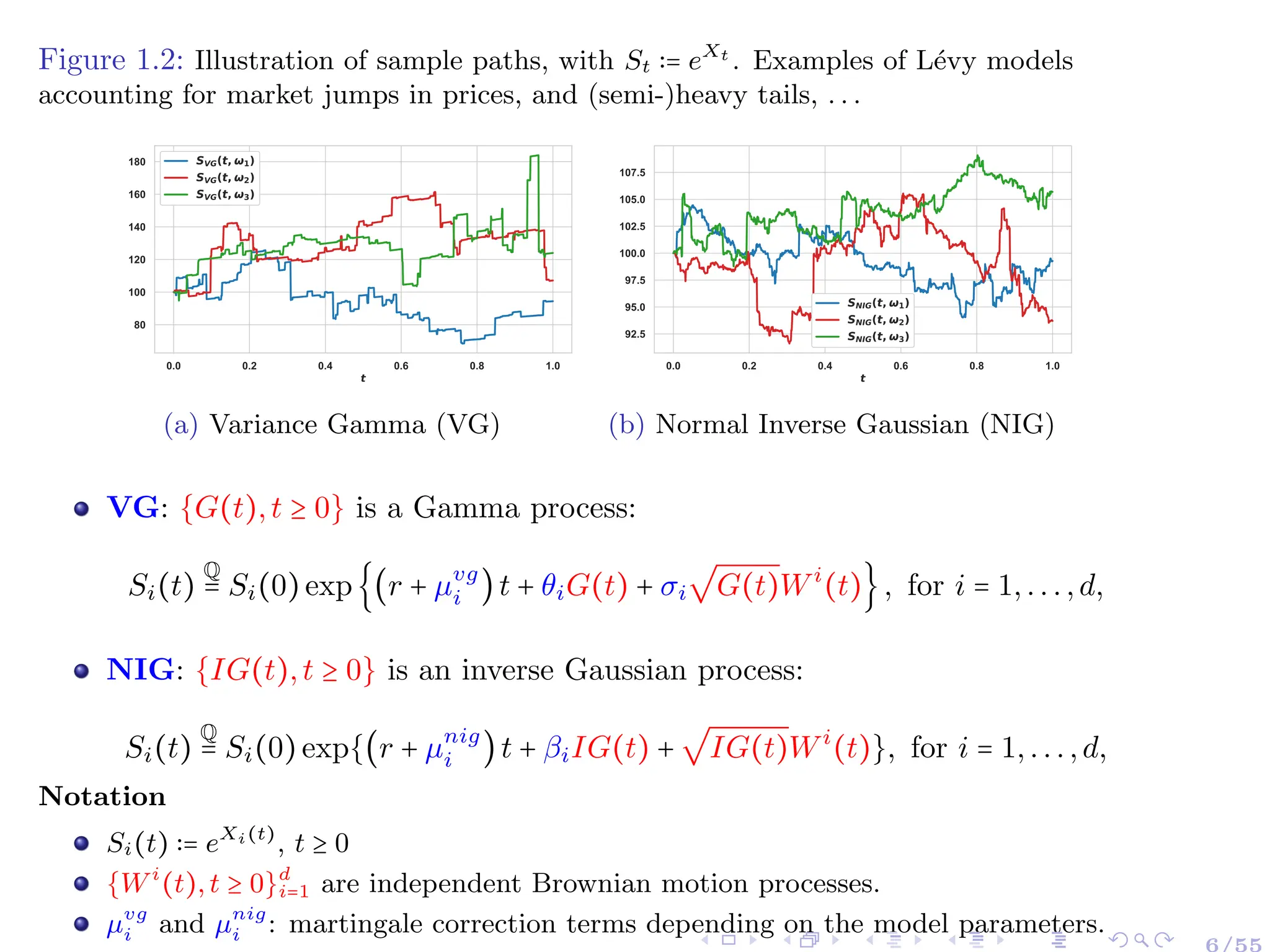
Figure 1.2: Illustration of sample paths, with St ∶= eXt
. Examples of Lévy models
accounting for market jumps in prices, and (semi-)heavy tails, . . .
0.0 0.2 0.4 0.6 0.8 1.0
t
80
100
120
140
160
180 SVG(t, ω1)
SVG(t, ω2)
SVG(t, ω3)
(a) Variance Gamma (VG)
0.0 0.2 0.4 0.6 0.8 1.0
t
92.5
95.0
97.5
100.0
102.5
105.0
107.5
SNIG(t, ω1)
SNIG(t, ω2)
SNIG(t, ω3)
(b) Normal Inverse Gaussian (NIG)
VG: {G(t),t ≥ 0} is a Gamma process:
Si(t)
Q
= Si(0)exp{(r + µvg
i )t + θiG(t) + σi
√
G(t)Wi
(t)}, for i = 1,...,d,
NIG: {IG(t),t ≥ 0} is an inverse Gaussian process:
Si(t)
Q
= Si(0)exp{(r + µnig
i )t + βiIG(t) +
√
IG(t)Wi
(t)}, for i = 1,...,d,
Notation
Si(t) ∶= eXi(t)
, t ≥ 0
{Wi
(t), t ≥ 0}d
i=1 are independent Brownian motion processes.
µvg
i and µnig
i : martingale correction terms depending on the model parameters.

Numerical Integration Methods
Task ((Multi-Asset) Option Pricing and Beyond): Compute
efficiently (up to discount factor)
E[P(X(T)) ∣ X(0) = x0] = ∫
Rd
P(x) ρXT ∣x0
(x) dx
Features of the problem
P(⋅) is non-smooth.
The pdf, ρXT
sample from.
Challenges
1 Monte Carlo method has a convergence rate independent of the
problem’s dimension and integrand’s regularity BUT can be very slow.
2 non-smoothness of P(⋅) and the high dimensionality ⇒ deteriorated
convergence of deterministic quadrature methods.

Numerical Integration Methods: Sampling in [0,1]2
E[P(X(T))] = ∫Rd P(x)ρXT
(x)dx ≈ ∑
M
m=1 ωmP (Ψ(um)) (Ψ ∶ [0,1]d
→ Rd
).
Monte Carlo (MC)
0 0.2 0.4 0.6 0.8 1
u1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u2
Tensor Product Quadrature
0 0.2 0.4 0.6 0.8 1
u1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u2
Quasi-Monte Carlo (QMC)
0 0.2 0.4 0.6 0.8 1
u1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u2
Adaptive Sparse Grids Quadrature
0 0.2 0.4 0.6 0.8 1
u1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u2

Fast Convergence: When Regularity Meets
Structured Sampling
Monte Carlo (MC)
(-) Slow convergence:
O(M− 1
2 ).
(+) Rate independent of
dimension and regularity
of the integrand.
Tensor Product Quadrature
Convergence: O(M− r
d )
(Davis et al. 2007).
r > 0 being the order of
bounded total
derivatives of the
integrand.
Quasi-Monte Carlo (QMC)
Optimal Convergence: O(M−1
)
(Dick et al. 2013).
Requires the integrability of first
order mixed partial derivatives
of the integrand.
Worst Case Convergence: O(M−1/2
).
Adaptive Sparse Grids Quadrature
Convergence: O(M− p
2 ) (Chen 2018;
Ernst et al. 2018).
p > 1 is related to the order of
bounded weighted mixed
(partial) derivatives of the
integrand.

Challenge 1: Original problem is non smooth (low regularity)
x1
4
2
0
2
4
x
2
4
2
0
2
4
P(x
1
,
x
2
)
0.0
0.2
0.4
0.6
0.8
(a) Basket Put
x1
0.0
0.2
0.4
0.6
0.8
1.0
x
2
0.0
0.2
0.4
0.6
0.8
1.0
P
(
x
1
,
x
2
)
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
(b) Call on min
x1
0
1
2
3
4
5
6
7
x
2
0
1
2
3
4
5
6
7
P(x
1
,
x
2
)
0.0
0.2
0.4
0.6
0.8
1.0
(c) Cash-or-nothing
Solution: Uncover the available hidden regularity in the
problem
1 Analytic smoothing (He et al. 2017; Bayer et al. 2018;
Ben Hammouda et al. 2020): taking conditional expectations over
subset of integration variables. / Good choice not always trivial.
2 Numerical smoothing (Kuo et al. 2018; Ben Hammouda et al.
2022; Ben Hammouda et al. 2024b): / Attractive when explicit
smoothing or Fourier mapping not possible.
3 Mapping the problem to the Fourier space (Today’s talk)
(Ben Hammouda et al. 2023; Ben Hammouda et al. 2024a).
" Characteristic function available.

Smoothing via Fourier transform
x1
4
2
0
2
4
x
2
4
2
0
2
4
P(x
1
,
x
2
)
0.0
0.2
0.4
0.6
0.8
(a) Payoff: Basket put
u1
20
10
0
10
20
u
2
20
10
0
10
20
|P(u
1
,
u
2
)|
1e
9
0.0
0.5
1.0
1.5
2.0
2.5
(b) Fourier Transform
x1
0
1
2
3
4
5
6
7
x
2
0
1
2
3
4
5
6
7
P(x
1
,
x
2
)
0.0
0.2
0.4
0.6
0.8
1.0
(a) Payoff:
Cash-or-nothing
u1
15
10
5
0
5
10
15
u
2
15
10
5
0
5
10
15
|P(u
1
,
u
2
)|
0.002
0.000
0.002
0.004
0.006
x1
2 1 0 1 2 3 4 5
x
2
2
1
0
1
2
3
4
5
P(x
1
,
x
2
)
0
20
40
60
80
100
120
140
(a) Payoff: Call on min
u1
30
20
10
0
10
20
30
u
2
30
20
10
0
10
20
30
|P(u
1
,
u
2
)|
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
11/55

5 Conclusions
11/55

Fourier Pricing Formula in d Dimensions
Assumption 2.1
1 x ↦ P(x) is continuous on Rd
(can be replaced by additional assumptions on XT ).
2 δP ∶= {R ∈ Rd
∶ x ↦ eR′x
P(x) ∈ L1
bc(Rd
) and y ↦ ̂
P(y + iR) ∈ L1
(Rd
)} ≠ ∅.
(strip of analyticity of ̂
P(⋅))
3 δX ∶= {R ∈ Rd
∶ y ↦∣ ΦXT
(y + iR) ∣< ∞,∀ y ∈ Rd
} ≠ ∅. (strip of analyticity of ΦXT (⋅))
Proposition (Ben Hammouda et al. 2023 (Extension of (Lewis 2001) in 1D and based on
(Eberlein et al. 2010))
Under Assumptions 1, 2 and 3, and for R ∈ δV ∶= δP ∩ δX, the option value on d stocks is
V (ΘX,Θp) ∶= e−rT
E[P(XT)] = ∫
Rd
P(x) ρXT
(x) dx (1)
= (2π)−d
e−rT
∫
Rd
R(ΦXT
(y + iR) ̂
P(y + iR))dy.
Notation
ΘX,Θp: the model and payoff parameters, respectively;
̂
P(⋅): the extended Fourier transform of the payoff P(⋅) ( ̂
P(z) ∶= ∫Rd e−iz′
⋅x
P(x)dx, for z ∈ Cd
);
XT : vector of log-asset prices at time T, with extended characteristic function ΦXT
(⋅) (i.e.,
Φ ∶= ̂
ρ);
R ∈ Rd
: damping parameters ensuring integrability and controlling the integration contour.
R[⋅]: real part of the argument. i: imaginary unit. 12/55

Fourier Pricing Formula in d Dimensions
Proof (Ben Hammouda et al. 2023).
Using the inverse generalized Fourier transform and Fubini theorems:
V (ΘX,ΘP ) = e−rT
E[P(XT)]
= e−rT
E[(2π)−d
R(∫
Rd
ei(y+iR)′
XT ̂
P(y + iR)dy)], R ∈ δP
= (2π)−d
e−rT
R(∫
Rd
E[ei(y+iR)′
XT
] ̂
P(y + iR)dy), R ∈ δV ∶= δP ∩ δX
= (2π)−d
e−rT
∫
Rd
R(ΦXT
(y + iR) ̂
P(y + iR))dy, R ∈ δV
Notation 2.2 (Integrand)
Given R ∈ δV ⊆ Rd
, we define the integrand of interest by
g (y;R,ΘX,ΘP ) ∶= (2π)−d
e−rT
R[ΦXT
(y + iR) ̂
P(y + iR)], y ∈ Rd
, (2)
13/55

Characteristic Functions: Illustrations
Table 1: ΦXT
(z) = exp(iz′
(X0 + (r + µ)T))ϕXT
(z): extended characteristic function of various
pricing models. I[⋅]: the imaginary part of the argument. Kλ(⋅) is the Bessel function of the
second kind. GH coincides with NIG for λ = −1
2
.
Model ϕXT
(z),z ∈ Cd
, I[z] ∈ δX
GBM exp(−T
2
z′
Σz)
VG (1 − iνz′
θ + 1
2
νz′
Σz)
−T /ν
GH ( α2
−β⊺
∆β
α2−β⊺
∆β+z⊺∆z−2iβ⊺
∆z
)
λ/2 Kλ(δT
√
α2−β⊺
∆β+z⊺∆z−2iβ⊺
∆z)
Kλ(δT
√
α2−β⊺
∆β)
NIG exp(δT (
√
α2 − β′
∆β −
√
α2 − (β + iz)′∆(β + iz)))
Table 2: Strip of analyticity, δX, of ΦXT
(⋅) (Eberlein et al. 2010)
Model δX
GBM Rd
VG {R ∈ Rd
,(1 + νθ′
R − 1
2
νR′
ΣR) > 0}
GH, NIG {R ∈ Rd
,(α2
− (β − R)′
∆(β − R)) > 0}
Notation:
Σ: Covariance matrix for the Geometric Brownian Motion (GBM) model.
ν > 0, θ, σ, Σ: Variance Gamma (VG) model parameters.
α, δ > 0, β, ∆: Normal Inverse Gaussian (NIG) and Generalized Hyperbolic (GH) model parameters.
µ: martingale correction terms depending on the model parameters.
14/55

Payoff Fourier Transforms: Illustration
Table 3: Fourier Transforms of (scaled) Payoff Functions, z ∈ Cd
. Γ(z) is the
complex Gamma function defined for z ∈ C with R[z] > 0.
Payoff P(XT ) ̂
P(z)
Basket put max(1 − ∑d
i=1 eXi
T ,0)
∏d
j=1 Γ(−izj)
Γ(−i ∑d
j=1 zj+2)
Call on min max(min(eX1
T ,...,eXd
T ) − 1,0) 1
(i(∑d
j=1 zj)−1) ∏d
j=1(izj)
CON put ∏d
j=1 1
{e
X
j
T <1 }
(Xj
T ) ∏d
j=1 (− 1
izj
)
Table 4: Strip of analyticity, δP , of ̂
P(⋅).
Payoff δP
Basket put {R ∈ Rd
,Ri > 0 ∀i ∈ {1,...,d}}
Call on min {R ∈ Rd
, Ri < 0 ∀i ∈ {1...d}, ∑d
i=1 Ri < −1}
CON put {Rj > 0}
15/55

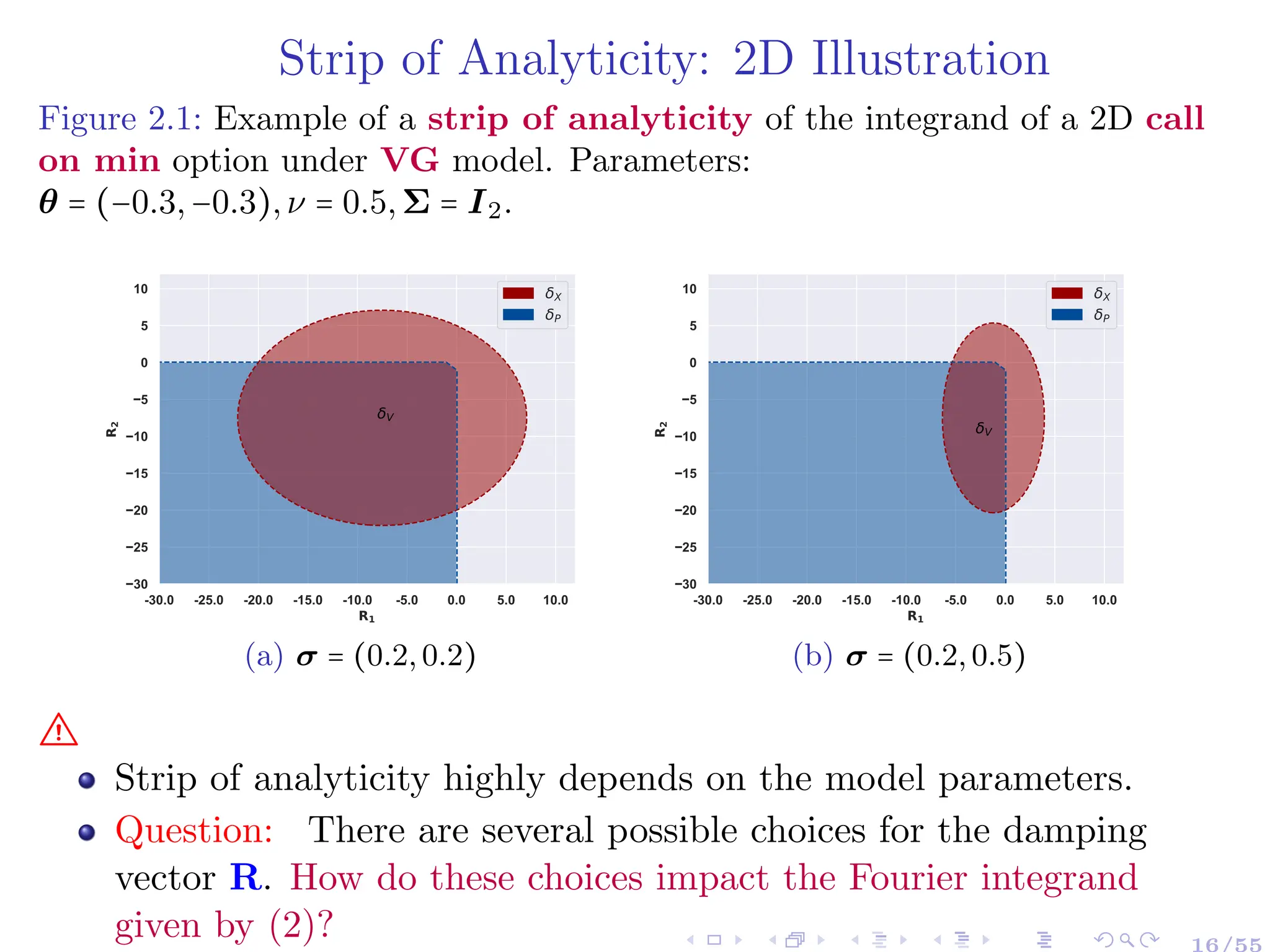
Strip of Analyticity: 2D Illustration
Figure 2.1: Example of a strip of analyticity of the integrand of a 2D call
on min option under VG model. Parameters:
θ = (−0.3,−0.3),ν = 0.5,Σ = I2.
-30.0 -25.0 -20.0 -15.0 -10.0 -5.0 0.0 5.0 10.0
R1
30
25
20
15
10
5
0
5
10
R
2
V
X
P
(a) σ = (0.2, 0.2)
-30.0 -25.0 -20.0 -15.0 -10.0 -5.0 0.0 5.0 10.0
R1
30
25
20
15
10
5
0
5
10
R
2
V
X
P
(b) σ = (0.2, 0.5)
"
Strip of analyticity highly depends on the model parameters.
Question: There are several possible choices for the damping
vector R. How do these choices impact the Fourier integrand
given by (2)? 16/55

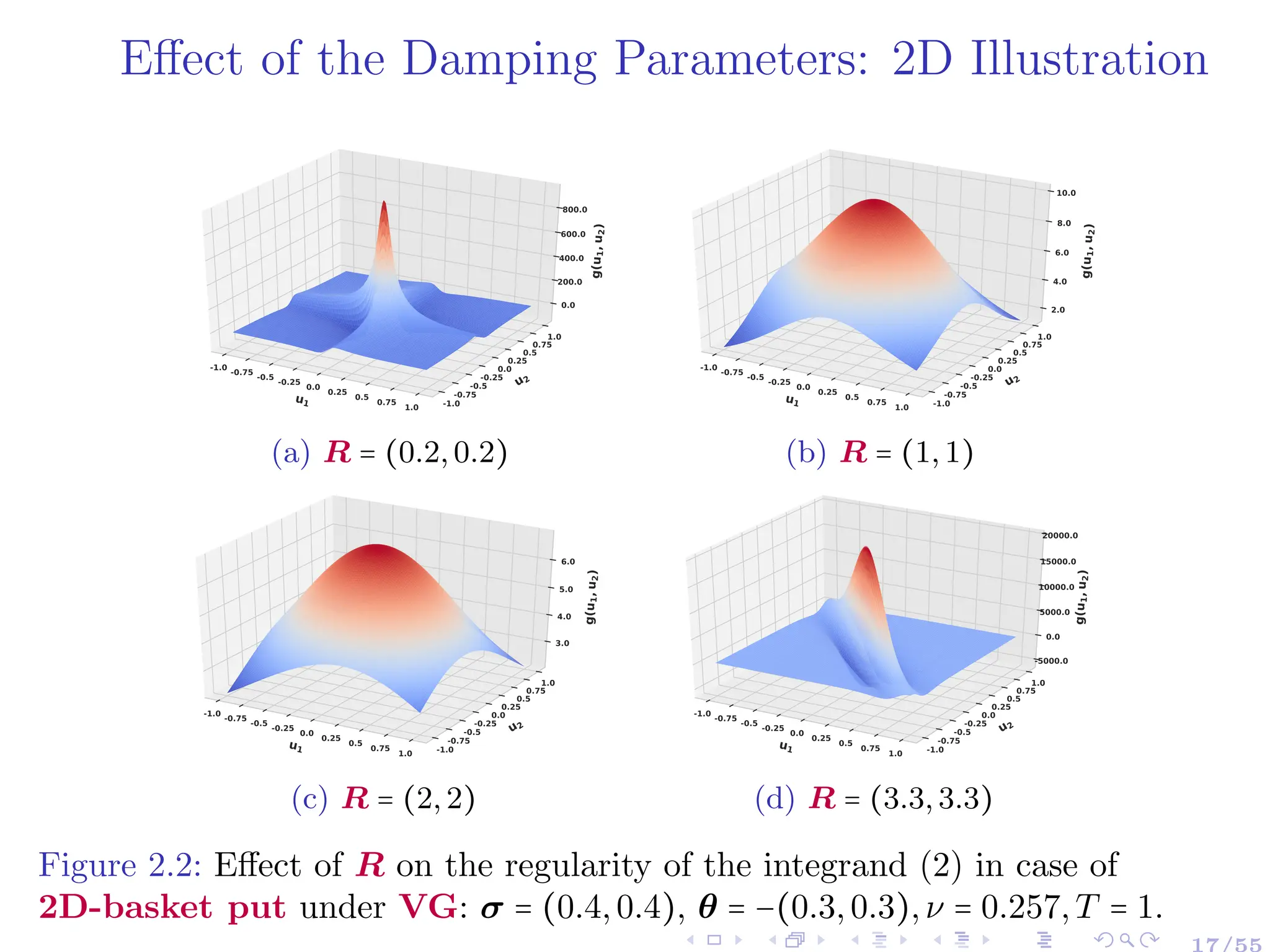
Effect of the Damping Parameters: 2D Illustration
u1
-1.0 -0.75 -0.5 -0.25 0.0 0.25 0.5 0.75 1.0
u2
-1.0
-0.75
-0.5
-0.25
0.0
0.25
0.5
0.75
1.0
g(u
1
,
u
2
)
0.0
200.0
400.0
600.0
800.0
(a) R = (0.2, 0.2)
u1
-1.0 -0.75 -0.5 -0.25 0.0 0.25 0.5 0.75 1.0
u2
-1.0
-0.75
-0.5
-0.25
0.0
0.25
0.5
0.75
1.0
g(u
1
,
u
2
)
2.0
4.0
6.0
8.0
10.0
(b) R = (1, 1)
u1
-1.0 -0.75 -0.5 -0.25 0.0 0.25 0.5 0.75 1.0
u2
-1.0
-0.75
-0.5
-0.25
0.0
0.25
0.5
0.75
1.0
g(u
1
,
u
2
)
3.0
4.0
5.0
6.0
(c) R = (2, 2)
u1
-1.0 -0.75 -0.5 -0.25 0.0 0.25 0.5 0.75 1.0
u2
-1.0
-0.75
-0.5
-0.25
0.0
0.25
0.5
0.75
1.0
g(u
1
,
u
2
)
-5000.0
0.0
5000.0
10000.0
15000.0
20000.0
(d) R = (3.3, 3.3)
Figure 2.2: Effect of R on the regularity of the integrand (2) in case of
2D-basket put under VG: σ = (0.4,0.4), θ = −(0.3,0.3),ν = 0.257,T = 1.
17/55

Challenge 2: The choice of the damping parameters
Damping parameters, R, ensure integrability and control the
regularity of the integrand
1 No precise analysis of the effect of the damping parameters on
the computational performance of numerical quadrature
methods.
2 No guidance on how to choose them to speed up convergence.
Solution: (Ben Hammouda et al. 2023)
Based on contour integration error estimates:
Parametric smoothing of the Fourier integrand via an (generic)
optimization rule for the choice of damping parameters.
⇒ speed up convergence.
18/55

5 Conclusions
18/55

Optimal Damping Rule: Characterization
The analysis of the quadrature error can be performed through two
representations:
1 Error estimates based on high-order derivatives for a smooth
function g:
▸ (-) High-order derivatives are usually challenging to estimate and
control.
▸ (-) Will result in a complex rule for optimally choosing the damping
parameters.
2 Error estimates, based on contour integration (Cauchy’s integral
theorem), valid for functions that can be extended holomorphically
into the complex plane
▸ (+) Corresponds to our case in Eq (2).
▸ (+) Will result in a simple rule for optimally choosing the damping
parameters.
19/55

Near-Optimal Damping Rule: Theoretical Argument
Theorem 3.1 (Error Estimate Based on Contour Integration)
Assuming f can be extended analytically along a sizable contour, C ⊇ [a,b], in
the complex plane, and f has no singularities in C, then we have,
∣EQN
[f]∣ ∶= ∣∫
b
a
f(x)λ(x)dx −
N
∑
k=1
f (xk)wk∣
= ∣
1
2πi
∮
C
KN (z)f(z)dz∣ ≤
1
2π
sup
z∈C
∣f(z)∣∮
C
∣KN (z)∣dz,
(3)
(Ben Hammouda et al. 2023) proves the extension to the
multivariate setting.
Notation:
KN (z) =
HN (z)
πN (z) , HN (z) = ∫
b
a λ(x)
πN (x)
z−x dx.
πN (⋅): the roots of the orthogonal polynomial related to the considered
quadrature with weight function λ(⋅).
20/55

Near-Optimal Damping Rule
Recall: our Fourier integrand is:
g (y;R) = (2π)−d
e−rT
R(ΦXT
(y + iR) ̂
P(y + iR)), y ∈ Rd
, R ∈ δV ⊆ Rd
Based on the error bound (3), we propose an optimization rule for
the choice of the damping parameters :
R∗
∶= R∗
(ΘX,ΘP ) = arg min
R∈δV
sup
y∈Rd
∣g (y;R,ΘX,ΘP )∣, (4)
R∗
∶= (R∗
1,...,R∗
d) denotes the optimal damping parameters.
The optimization problem in (4) can be simplified
Proposition (Ben Hammouda et al. 2023)
For the Fourier integrand g(⋅) defined by (2), we have
R∗
= arg min
R∈δV
sup
y∈Rd
∣g (y;R,ΘX,ΘP )∣ = arg min
R∈δV
g (0Rd ;R,ΘX,ΘP ). (5)
R: the numerical approximation of R∗
using trust- region method.
21/55

Near-Optimal Damping Rule
g (y;R) = (2π)−d
e−rT
R(ΦXT
(y + iR) ̂
P(y + iR)), y ∈ Rd
, R ∈ δV ⊆ Rd
Based on the error bound (3), we propose an optimization rule for
the choice of the damping parameters :
R∗
∶= R∗
(ΘX,ΘP ) = arg min
R∈δV
sup
y∈Rd
∣g (y;R,ΘX,ΘP )∣, (4)
R∗
∶= (R∗
1,...,R∗
d) denotes the optimal damping parameters.
The optimization problem in (4) can be simplified
Proposition (Ben Hammouda et al. 2023)
For the Fourier integrand g(⋅) defined by (2), we have
R∗
= arg min
R∈δV
sup
y∈Rd
∣g (y;R,ΘX,ΘP )∣ = arg min
R∈δV
g (0Rd ;R,ΘX,ΘP ). (5)
R: the numerical approximation of R∗
using trust- region method.

Near-Optimal Damping Rule: 1D Illustration
g (u;R) = (2π)−d
e−rT
R(ΦXT
(u + iR) ̂
P(u + iR)), u ∈ Rd
, R ∈ δV ⊆ Rd
Figure 3.1: (left) Shape of the integrand w.r.t the damping parameter, R.
(right) Convergence of relative quadrature error w.r.t. number of quadrature
points, using Gauss-Laguerre quadrature for the European put option under
VG: S0 = K = 100,r = 0,T = 1,σ = 0.4,θ = −0.3,ν = 0.257.
−4 −2 0 2 4
u
0
5
10
15
20
g(u)
R = 1
R = 3
R = 4
R = 2.29
101
N
10−3
10−2
10−1
ε
R
R = 1
R = 3
R = 4
R = 2.29

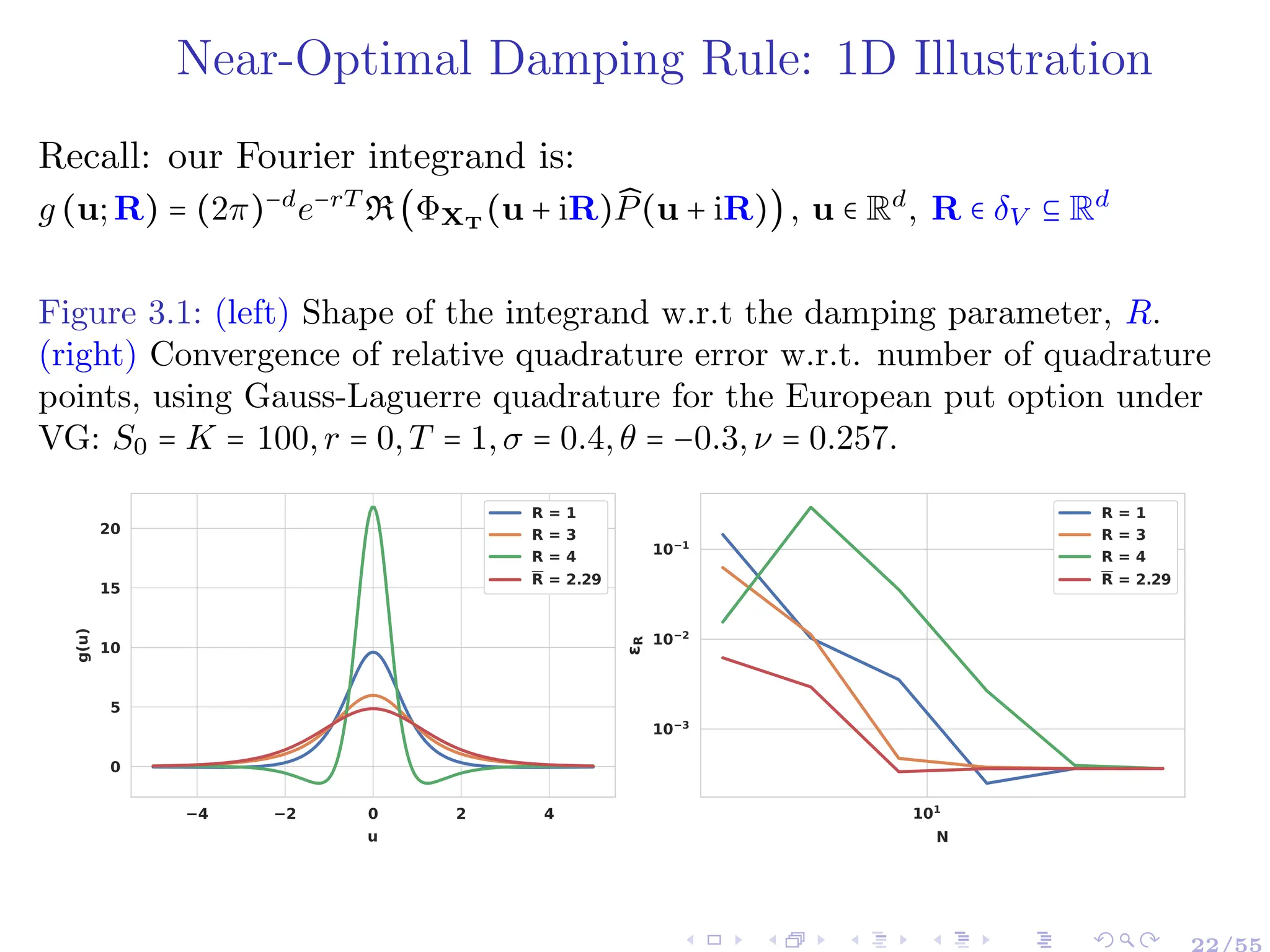
Option value on d stocks
(Multivariate Expectation of Interest)
g (y;R) = (2π)−d
e−rT
R(ΦXT
(y + iR) ̂
P(y + iR)), y ∈ Rd
, R ∈ δV ⊆ Rd
Physical space:
E[P(X(T))] =
∫Rd P(x) ρXT
(x) dx
A non-smooth
d-dimensional
integration problem
Fourier space:
∫Rd g (y;R)dy
A highly-smooth
d-dimensional
integration problem
Fourier Mapping
+ Damping Rule

Challenge 3: Curse of dimensionality
Most proposed Fourier pricing methods efficient for only 1D/2D
options (Carr et al. 1999; Lewis 2001; Fang et al. 2009; Hurd et al. 2010)
Complexity of tensor product (TP) quadrature to solve (1) ↗ exponentially
with the dimension d (i.e, number of underlying assets).
2 3 4 5 6 7 8
dimension
10−1
100
101
102
103
104
Runtime
TP
TP
Figure 3.2: Call on min option under Normal Inverse Gaussian model: Runtime (in
sec) versus dimension for TP for a relative error TOL = 10−2
.
Solution: Effective treatment of the high dimensionality
1 (Ben Hammouda et al. 2023): Sparsification and
dimension-adaptivity techniques to accelerate convergence.
2 (Ben Hammouda et al. 2024a): Quasi-Monte Carlo (QMC) with
efficient domain transformation.

Challenge 3: Curse of dimensionality
Most proposed Fourier pricing methods efficient for only 1D/2D
options (Carr et al. 1999; Lewis 2001; Fang et al. 2009; Hurd et al. 2010)
Complexity of tensor product (TP) quadrature to solve (1) ↗ exponentially
with the dimension d (i.e, number of underlying assets).
2 3 4 5 6 7 8
dimension
10−1
100
101
102
103
104
Runtime
TP
TP
Figure 3.2: Call on min option under Normal Inverse Gaussian model: Runtime (in
sec) versus dimension for TP for a relative error TOL = 10−2
.
Solution: Effective treatment of the high dimensionality
1 (Ben Hammouda et al. 2023): Sparsification and
dimension-adaptivity techniques to accelerate convergence.
2 (Ben Hammouda et al. 2024a): Quasi-Monte Carlo (QMC) with
efficient domain transformation. 24/55

Quadrature Methods: Illustration of Grids Construction
Figure 3.3: N = 81 Clenshaw-Curtis quadrature points on [0,1]2
for (left) TP,
(center) sparse grids, (right) adaptive sparse grids quadrature
(ASGQ). The ASGQ is built for the function: f(u1,u2) = 1
u2
1+exp(10 u2)+0.3
0 0.2 0.4 0.6 0.8 1
u1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u2
0 0.2 0.4 0.6 0.8 1
u1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u2
0 0.2 0.4 0.6 0.8 1
u1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u2
25/55

Quadrature Methods
Naive Quadrature operator based on a Cartesian quadrature grid
∫
Rd
g(x)ρ(x)dx ≈
d
⊗
k=1
QNk
k [g] ∶=
N1
∑
i1=1
⋯
Nd
∑
id=1
wi1 ⋯wid
g (xi1 ,...,xid
)
" Caveat: Curse of dimension: i.e., total number of quadrature
points N = ∏d
k=1 Nk.
Solution:
1 Sparsification of the grid points to reduce computational work.
2 Dimension-adaptivity to detect important dimensions of the
integrand.
Notation:
{xik
,wik
}Nk
ik=1 are respectively the sets of quadrature points and
corresponding quadrature weights for the kth dimension, 1 ≤ k ≤ d.
QNk
k [.]: the univariate quadrature operator for the kth dimension.
26/55

1D Hierarchical Construction of Quadrature Methods
Let m(⋅) ∶ N+ → N+ be a strictly increasing function with m(1) = 1;
▸ β ∈ N+: hierarchical quadrature level.
▸ m(β) ∈ N+: number of quadrature points used at level β.
Hierarchical construction: example for level 3 quadrature Qm(3)
[g]:
Qm(3)
[g] = Qm(1)
´¹¹¹¹¹¸¹¹¹¹¹¶
∆m(1)
[g] + (Qm(2)
− Qm(1)
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
∆m(2)
)[g] + (Qm(3)
− Qm(2)
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
∆m(3)
)[g],
where ∆m(β)
∶= Qm(β)
− Qm(β−1)
, Qm(0)
= 0: univariate detail operator.
The exact value of the integral can be written as a series expansion of
detail operators
∫
R
g(x)dx =
∞
∑
β=1
∆m(β)
[g],
27/55

Hierarchical Sparse grids: Construction
Let β = [β1,...,βd] ∈ Nd
+, m(β) ∶ N+ → N+ an increasing function,
1 1D quadrature operators: Q
m(βk)
k on m(βk) points, 1 ≤ k ≤ d.
2 Detail operator: ∆
m(βk)
k = Q
m(βk)
k − Q
m(βk−1)
k , Q
m(0)
k = 0.
3 Hierarchical surplus: ∆m(β)
= ⊗d
k=1 ∆
m(βk)
k .
4 Hierarchical sparse grid approximation: on an index set I ⊂ Nd
QI
d [g] = ∑
β∈I
∆m(β)
[g] (6)
28/55

Grids Construction
Tensor Product (TP) approach: I ∶= Iℓ = {∣∣ β ∣∣∞≤ ℓ; β ∈ Nd
+}.
Regular sparse grids (SG): I ∶ Iℓ = {∣∣ β ∣∣1≤ ℓ + d − 1; β ∈ Nd
+}
Adaptive sparse grids (ASG): Adaptive and a posteriori
construction of I = IASGQ
by profit rule
IASGQ
= {β ∈ Nd
+ ∶ Pβ ≥ T}, with Pβ =
∣∆Eβ∣
∆Wβ
:
▸ ∆Eβ = ∣Q
I∪{β}
d [g] − QI
d [g]∣ (error contribution);
▸ ∆Wβ = Work[Q
I∪{β}
d [g]] − Work[QI
d [g]] (work contribution).
Figure 3.4: 2-D Illustration (Chen 2018): Admissible index sets I (top) and
corresponding quadrature points (bottom). Left: TP; middle: SG; right: ASG .
29/55

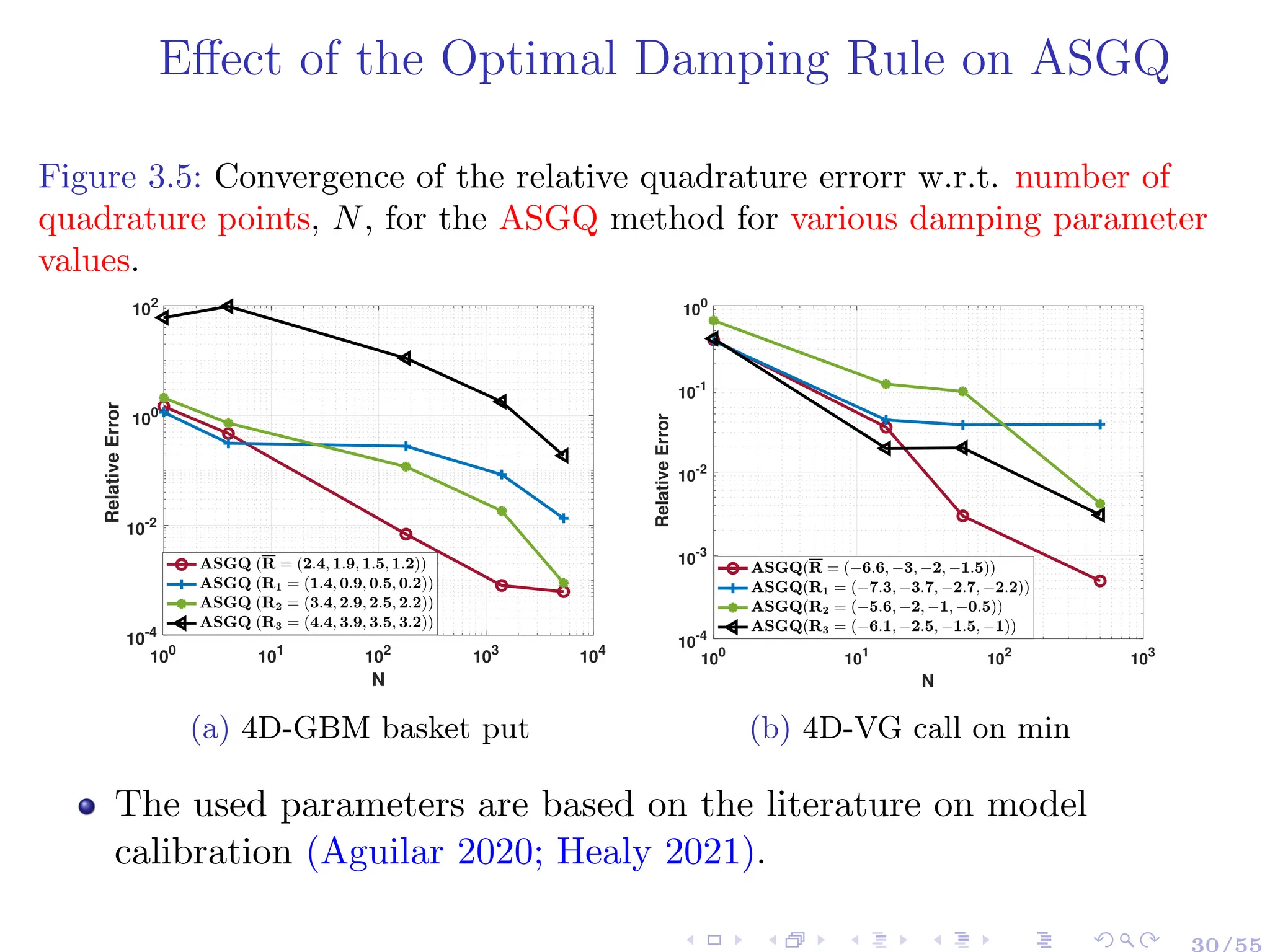
Effect of the Optimal Damping Rule on ASGQ
Figure 3.5: Convergence of the relative quadrature errorr w.r.t. number of
quadrature points, N, for the ASGQ method for various damping parameter
values.
100
101
102
103
104
N
10-4
10-2
100
102
Relative
Error
(a) 4D-GBM basket put
100
101
102
103
N
10-4
10-3
10-2
10-1
100
Relative
Error
(b) 4D-VG call on min
The used parameters are based on the literature on model
calibration (Aguilar 2020; Healy 2021).
30/55

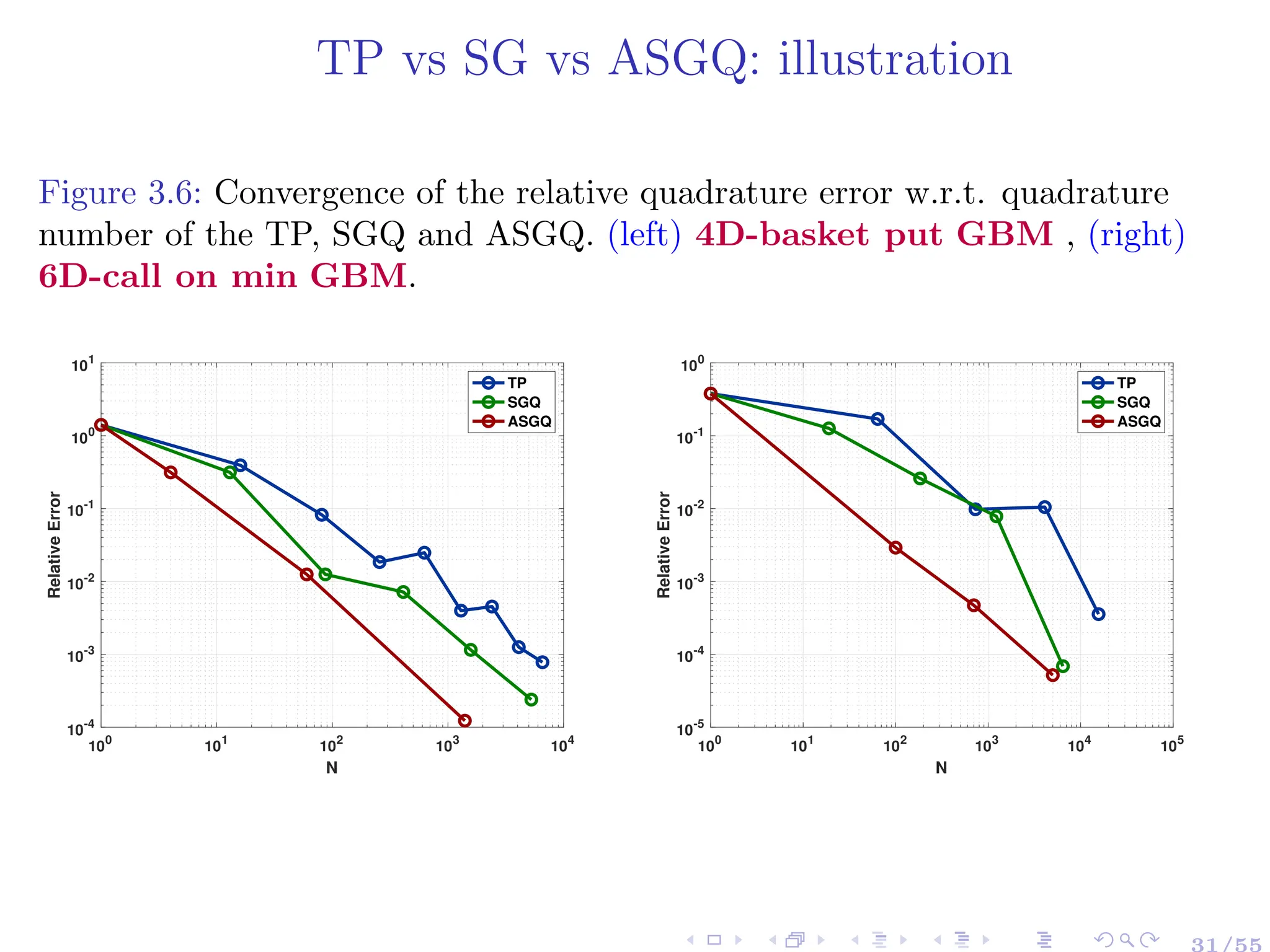
TP vs SG vs ASGQ: illustration
Figure 3.6: Convergence of the relative quadrature error w.r.t. quadrature
number of the TP, SGQ and ASGQ. (left) 4D-basket put GBM , (right)
6D-call on min GBM.
10
0
10
1
10
2
10
3
10
4
N
10-4
10-3
10
-2
10
-1
100
10
1
Relative
Error
TP
SGQ
ASGQ
10
0
10
1
10
2
10
3
10
4
10
5
N
10-5
10-4
10
-3
10
-2
10-1
10
0
Relative
Error
TP
SGQ
ASGQ

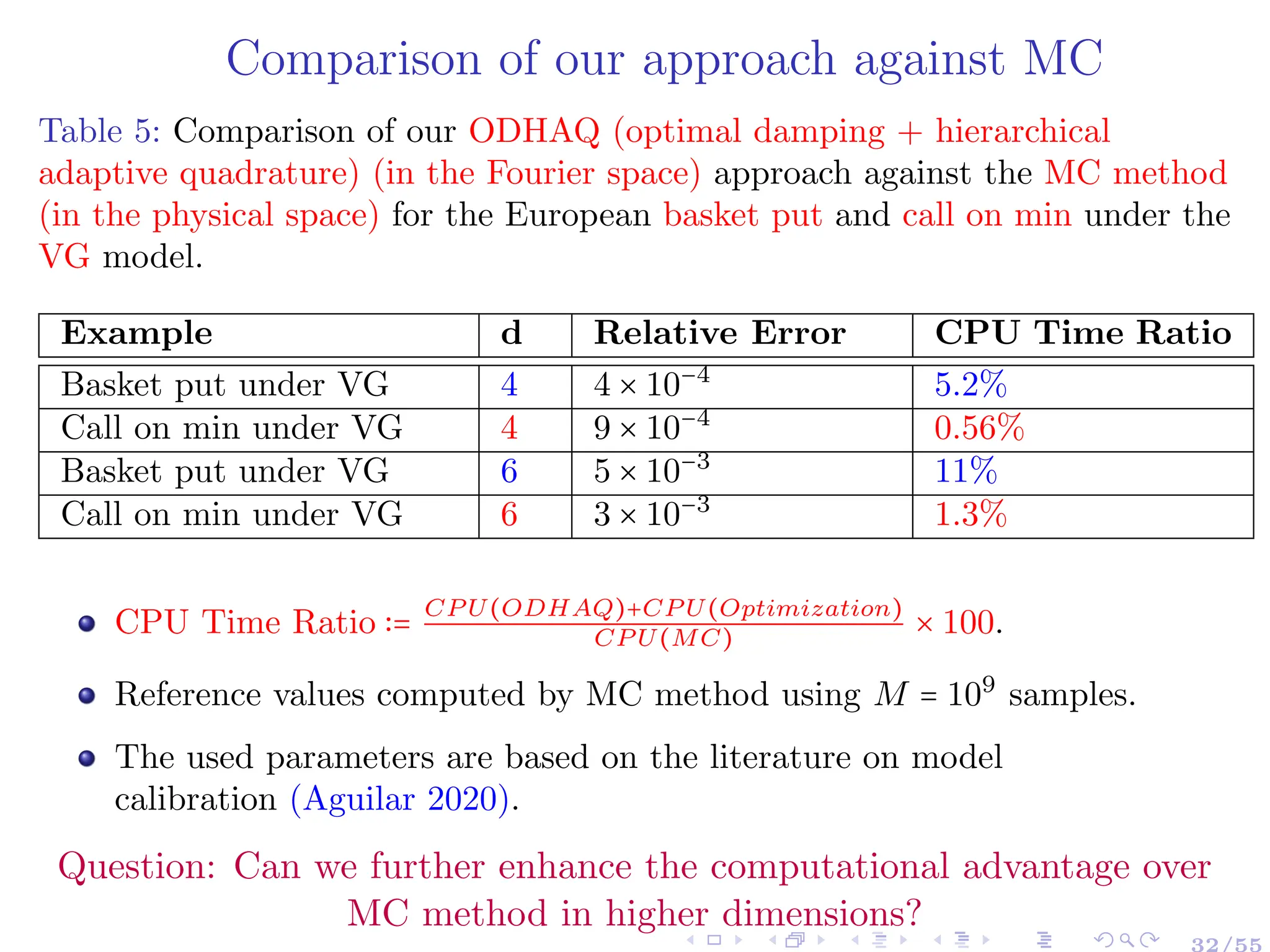
Comparison of our approach against MC
Table 5: Comparison of our ODHAQ (optimal damping + hierarchical
adaptive quadrature) (in the Fourier space) approach against the MC method
(in the physical space) for the European basket put and call on min under the
VG model.
Example d Relative Error CPU Time Ratio
Basket put under VG 4 4 × 10−4
5.2%
Call on min under VG 4 9 × 10−4
0.56%
Basket put under VG 6 5 × 10−3
11%
Call on min under VG 6 3 × 10−3
1.3%
CPU Time Ratio ∶= CP U(ODHAQ)+CP U(Optimization)
CP U(MC)
× 100.
Reference values computed by MC method using M = 109
samples.
The used parameters are based on the literature on model
calibration (Aguilar 2020).
Question: Can we further enhance the computational advantage over
MC method in higher dimensions?
32/55

5 Conclusions
32/55

Quasi Monte Carlo methods and Discrepancy
Let P = {ξ1,...ξM } be a set of points ξi ∈ [0,1]N
and f ∶ [0,1]N
→ R a
continuous function. A Quasi Monte Carlo (QMC) method to
approximate IN (f) = ∫[0,1]N f(y)dy is an equal weight cubature
formula of the form
IN,M (f) =
1
M
M
∑
i=1
f(ξi) .
The key concept in the analysis of QMC methods is the one of
discrepancy. Notation: for x ∈ [0,1]N
let
[0,x] ∶= [0,x1] × ... × [0,xN ]. Then
V ol([0,x]) ≈ ̂
V olP ([0,x]) ∶=
# points in [0,x]
M
for a given point set P = {ξ1,...ξM }.
Local discrepancy function ∆P ∶[0,1]N
→ [−1,1]
∆P (x) ∶= ̂
V olP ([0,x]) − V ol([0,x])
=
1
M
M
∑
i=1
1[0,x](ξi) −
N
∏
i=1
xi
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
x
33/55

Quasi-Monte Carlo (QMC):
Need for Domain Transformation
g (y;R) = (2π)−d
e−rT
R(ΦXT
(y + iR) ̂
P(y + iR)), y ∈ Rd
, R ∈ δV ⊂ Rd
Our Fourier integrand is in Rd
BUT QMC constructions are restricted
to the generation of low-discrepancy point sets on [0,1]d
.
0 0.2 0.4 0.6 0.8 1
u1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u2
Figure 4.1: shifted QMC (Lattice rule) low discrepancy points (LDP)
in 2D
⇒ Need to transform the integration domain
34/55

Quasi-Monte Carlo (QMC):
Need for Domain Transformation
g (y;R) = (2π)−d
e−rT
R(ΦXT
(y + iR) ̂
P(y + iR)), y ∈ Rd
, R ∈ δV ⊂ Rd
Our Fourier integrand is in Rd
BUT QMC constructions are restricted
to the generation of low-discrepancy point sets on [0,1]d
.
⇒ Need to transform the integration domain
Compositing with inverse cumulative distribution function, we obtain
∫
Rd
g(y)dy = ∫
[0,1]d
g ○ Ψ−1
(u;Λ)
ψ ○ Ψ−1(u;Λ)
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
=∶g̃(u;Λ)
du.
▸ ψ(⋅;Λ): a probability density function (PDF) with parameters Λ.
▸ Ψ(⋅;Λ): the cumulative distribution function (CDF) corresponding
to ψ(⋅;Λ).
34/55

Randomized Quasi-Monte Carlo (RQMC)
The transformed integration problem reads now:
∫
[0,1]d
g ○ Ψ−1
(u;Λ)
ψ ○ Ψ−1(u;Λ)
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
=∶g̃(u;Λ)
du. (7)
Once the choice of ψ(⋅;Λ) (respectively Ψ−1
(⋅;Λ)) is determined,
the RQMC estimator of (7) can be expressed as follows:
QRQMC
N,S [g̃] ∶=
1
S
S
∑
i=1
1
N
N
∑
n=1
g̃ (u(s)
n ;Λ), (8)
▸ {un}N
n=1 is the sequence of deterministic QMC points in [0,1]d
▸ For n = 1,...,N, {u
(s)
n }S
s=1: obtained by an appropriate
randomization of {un}N
n=1, e.g.,
u
(s)
n = {un + ηs}, with {ηs}S
s=1
i.i.d
∼ U([0,1]d
) and {⋅} is the
modulo-1 operator.
35/55

Previous literature (Kuo et al. 2011; Nichols et al. 2014; Ouyang et al.
2023) considers a different setting (more straightforward) for QMC:
Transformation for a weighted integration problem
(i.e., ∫Rd g(y) ρ(y) dy),
In the physical space
Assumes an independence structure
Our Setting
Recall the transformed integration problem in the Fourier space
∫
[0,1]d
g ○ Ψ−1
(u;Λ)
ψ ○ Ψ−1(u;Λ)
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
=∶g̃(u;Λ)
du.
⇒ We need to design a transformation adapted to our setting and take
into account possible dependencies between the dimensions (i.e.,
correlation between asset prices). 36/55

Challenge 4: Deterioration of QMC convergence if ψ
or/and Λ are badly chosen
Observe: The denominator of g̃(u) =
g○Ψ−1(u;Λ)
ψ○Ψ−1(u;Λ)
decays to 0 as
uj → 0,1 for j = 1,...,d.
The transformed integrand may have singularities near the
boundary of [0,1]d
⇒ Deterioration of QMC convergence.
−20 −15 −10 −5 0 5 10 15 20
u
0.0
0.2
0.4
0.6
0.8
g
(
u
)
(a) Original Fourier integrand
for call option under GBM
0.0 0.2 0.4 0.6 0.8 1.0
u
0
10
20
30
40
50
60
70
̃
g
(
u
)
̃ ̃
σ = 1.0
̃ ̃
σ = 5.0
̃ ̃
σ = 9.0
(b) Transformed integrand, based
on Gaussian density with scale σ̃.
Questions
Q1: Which density to choose? Q2: How to choose its parameters?

How to choose ψ(⋅;Λ) (respectively Ψ−1(⋅;Λ) ) and
and its parameters, Λ?
For u ∈ [0,1]d
,R ∈ δV ⊂ Rd
, the transformed Fourier integrand reads:
g̃(u) =
g ○ Ψ−1
(u;Λ)
ψ ○ Ψ−1(u;Λ)
=
e−rT
(2π)d
R
⎡
⎢
⎢
⎢
⎣
̂
P(Ψ−1
(u) + iR)
ΦXT
(Ψ−1
(u) + iR)
ψ (Ψ−1(u))
⎤
⎥
⎥
⎥
⎦
.
⇒ Sufficient to design the domain transformation to control the growth
at the boundaries of the term
ΦXT
(Ψ−1(u)+iR)
ψ(Ψ−1(u))
(Conservative choice).
The payoff Fourier transforms ( ̂
P(⋅)) decay at a polynomial rate.
PDFs of the pricing models (light and semi-heavy tailed models), if
they exist, are much smoother than the payoff ⇒ the decay of their
Fourier transforms (charactersitic functions) is faster the one of the
payoff Fourier transform (Trefethen 1996; Cont et al. 2003).

Model-dependent Domain Transformation
Solution (Ben Hammouda et al. 2024a): Effective Domain
Transformation
1 Choose the density ψ(⋅;Λ) to asymptotically follow the same
functional form of the characteristic function.
© Advantage: Derive explicit and simple conditions relating the
transformation parameters Λ to the model parameters in ΦXT (⋅)
In (Ben Hammouda et al. 2024a), We derive the boundary growth
conditions on the transformed integrand for models with different
classes of decay of the characteristic functions, namely,
Light-tailed i.e., ∣ΦXT
(z)∣ ≤ C exp(−γ∣z∣2
) with C,γ > 0,z ∈ Cd
.
GBM model as an example.
Semi-heavy-tailed i.e., ∣ΦXT
(z)∣ ≤ C exp(−γ∣z∣) with
C,γ > 0,z ∈ Cd
. GH (NIG) model as an example.
Heavy-tailed i.e., ∣ΦXT
(z)∣ ≤ C (1 + ∣z∣2
)
−γ
for C > 0,γ > 1
2,z ∈ Cd
.
VG model as an example.
39/55

Model-dependent Domain Transformation
Solution (Ben Hammouda et al. 2024a): Effective Domain Transformation
1 Choose the density ψ(⋅;Λ) to asymptotically follow the same functional form of the
characteristic function.
© Advantage: Derive explicit and simple conditions relating the transformation parameters Λ
to the model parameters in ΦXT (⋅)
Table 6: Extended characteristic function: ΦXT
(z) = exp(iz′
X0)exp(iz′
µT)ϕXT
(z), and choice of ψ(⋅).
ϕXT
(z),z ∈ Cd
, I[z] ∈ δX ψ(y;Λ),y ∈ Rd
Gaussian (Λ = Σ̃):
GBM model: exp(−T
2
z′
Σz)
(2π)− d
2 (det(Σ̃))− 1
2 exp(−1
2
(y′
Σ̃
−1
y))
Generalized Student’s t (Λ = (ν̃,Σ̃)):
VG model: (1 − iνz′
θ + 1
2
νz′
Σz)
−T /ν Γ( ν̃+d
2
)(det(Σ̃))− 1
2
Γ( ν̃
2
)ν̃
d
2 π
d
2
(1 + 1
ν̃
(y′
Σ̃y))
− ν̃+d
2
NIG model: Laplace (Λ = Σ̃) and (v = 2−d
2
):
exp(δT (
√
α2 − β′
∆β −
√
α2 − (β + iz)′∆(β + iz)))
(2π)− d
2 (det(Σ̃))− 1
2 (y′
Σ̃
−1
y
2
)
v
2
Kv (
√
2y′Σ̃
−1
y)
Notation:
Σ: Covariance matrix for the Geometric Brownian Motion (GBM) model.
ν, θ, σ, Σ: Variance Gamma (VG) model parameters.
α, β, δ, ∆: Normal Inverse Gaussian (NIG) model parameters.
µ is the martingale correction term.
Kv(⋅): the modified Bessel function of the second kind.
40/55

Model-dependent Domain Transformation:
Case of Independent Assets
Using independence: Observe
ϕXT
(Ψ−1
(u)+iR)
ψ(Ψ−1(u))
= ∏
d
j=1
ϕ
X
j
T
(Ψ−1
(uj )+iRj )
ψj (Ψ−1(uj ))
1 Choose the density ψ(⋅;Λ) in the change of variable to asymptotically follow the same functional
form of the extended characteristic function.
2 Select the parameters Λ to control the growth of the integrand near the boundary of [0,1]d
i.e
limuj →0,1 g̃(uj) < ∞, j = 1,...,d.
Table 7: Choice of ψ(u;Λ) ∶= ∏
d
j=1 ψj(uj;Λ) and conditions on Λ for GBM, (ii) VG and (iii) NIG. See
(Ben Hammouda et al. 2024a) for the derivation.
Model ψj(yj;Λ) Growth condition on Λ
GBM
1
√
2σ̃j
2
exp(−
y2
j
2σ̃j
2 ) (Gaussian) σ̃j ≥ 1
√
T σj
VG
Γ( ν̃+1
2
)
√
ν̃πσ̃j Γ( ν̃
2
)
(1 +
y2
j
ν̃σ̃j
2 )
−(ν̃+1)/2
(t-Student) ν̃ ≤ 2T
ν
− 1,
σ̃j = (
νσ2
j ν̃
2
)
T
ν−2T
(ν̃)
ν
4T −2ν
NIG, GH
exp(−
∣yj ∣
σ̃j
)
2σ̃j
(Laplace) σ̃j ≥ 1
δT
" In case of equality conditions, the integrand still decays at the speed of the payoff transform.

Boundary Growth Conditions: GBM as Illustration
Consider the case of independent assets, s.t. the characteristic function can be
written as
ϕXT
(u) =
d
∏
j=1
ϕXj
T
(uj),u ∈ Rd
,
where
ϕXj
T
(uj) = exp(rT − i
σj
2
T
2
uj −
σj
2
T
2
u2
j )
For the domain transformation density, we propose ψ(u) = ∏
d
j=1 ψj(uj), with
ψj(uj) =
exp(−
u2
j
2σ̃2
j
)
√
2σ̃2
j
,uj ∈ R.
⇒ The transformed integrand can be written as (y ∈ [0,1]d
)
g̃(y) ∶= (2π)−d
e−rT
e−⟨R,X0⟩
R
⎡
⎢
⎢
⎢
⎢
⎣
ei⟨Ψ−1
(y),X0⟩ ̂
P (Ψ−1
(y) + iR)
d
∏
j=1
ϕXj
T
(Ψ−1
(yj) + iRj)
ψj(Ψ−1(yj))
⎤
⎥
⎥
⎥
⎥
⎦
.
42/55

Boundary Growth Condition: GBM
The term controlling the growth of the integrand near the boundary is
rj(yj) ∶=
ϕXj
T
(Ψ−1
(yj) + iRj)
ψj(Ψ−1(yj))
, yj ∈ [0,1]. (9)
After some simplifications (9) reduces to
rj(yj) = σ̃j exp(−(Ψ−1
(yj))2
(
Tσ2
j
2
−
1
2σ̃2
j
))
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
∶=T1(controls the growth of the integrand near the boundary)
×
√
2π exp(−iTΨ−1
(yj)(
σ2
j
2
+ σ2
j Rj) + R2
j Tσ2
j + rT)
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
∶=T2 (bounded)
,
If we set σ̃j ≥ 1
√
T σj
⇒ T1 < ∞ as yj → 0,1 (since (Ψ−1
(yj))2
→ +∞).
43/55

Effect of Domain Transformation on
RQMC Convergence
0.0 0.2 0.4 0.6 0.8 1.0
u
0
10
20
30
40
50
60
̃
g
(
u
)
̃ ̃
σ = 1.0
̃ ̃
σ = 5.0
̃ ̃
σ = 9.0
(a)
103 104
NxS
10−6
10−5
10−4
10−3
10−2
10−1
100
Relative
Statistical
Error
̃
σ=1.0
N−0.68
̃
σ=5.0
N−1.42
̃
σ=9.0
N−2.26
(b)
Figure 4.3: Call option under the NIG model: Effect of the parameter σ̃ of
the Laplace PDF on
(a) the shape of the transformed integrand g̃(u) and
(b) convergence of the relative statistical error of RQMC
N: number of QMC points; S = 32: number of digital shifts.
Boundary growth condition: σ̃ ≥ 1
T δ
= 5.
44/55

Effect of Domain Transformation on
RQMC Convergence
0.0 0.2 0.4 0.6 0.8 1.0
u
−5
0
5
10
15
20
25
30
35
̃
g
(
u
)
̃ ̃
ν = 3.0
̃ ̃
ν = 9.0
̃ ̃
ν = 15.0
(a)
103 104
NxS
10−8
10−7
10−6
10−5
10−4
10−3
10−2
Relative
Statistical
Error
̃
ν = 3.0
N−3.05
̃
ν = 9.0
N−1.35
̃
ν = 15.0
N−0.66
(b)
Figure 4.4: Call option under the VG model: Effect of the parameter ν̃ of
the t-student PDF on
(a) the shape of the transformed integrand g̃(u) and
(b) convergence of the RQMC error
N: number of QMC points; S = 32: number of digital shifts.
Boundary growth condition: ν̃ ≤ 2T
ν
− 1 = 9
45/55

Should Correlation Be Considered
in the Domain Transformation?
104
NxS
10−4
10−3
10−2
10−1
Relative
Statistical
Error
ρ= −0.7
N−0.99
ρ=0
N−1.48
ρ=0.7
N−0.69
Figure 4.5: Two-dimensional call on the minimum option under the GBM model:
Effect of the correlation parameter, ρ, on the convergence of RQMC.
For the domain transformation, we set σ̃j = 1
√
T σj
= 5, j = 1, 2. N: number of QMC
points; S = 32: number of digital shifts.
46/55

Case of Correlated Assets
Challenge 5: Numerical Evaluation of the inverse CDF Ψ−1
(⋅)
1 We can not evaluate the inverse CDF componentwise using the univariate inverse
CDF as in the independent case (Ψ−1
d (u) ≠ (Ψ−1
1 (u1),...,Ψ−1
1 (ud))).
2 The inverse CDF is not given in closed-form for most multivariate distributions,
and its numerical approximation is generally computationally expensive.
Observe: For Gaussian (normal) case: If Z ∼ N(0,Id) ⇒ X = L̃Z ∼ N(0,Σ̃) (L̃:
Cholesky factor of Σ̃) ⇒ we have
Ψ−1
nor,d(u;Σ̃) = L̃Ψ−1
nor,d(u;Id) = L̃(Ψ−1
nor,1(u1),...,Ψ−1
nor,1(ud))
General Solution: Avoid the expensive computation of the inverse CDF
1 We consider multivariate transformation densities, ψ(⋅,Λ), which belong to the
class of normal mean-variance mixture distributions:
i.e., for X ∼ ψ(⋅,Λ), we can write X = µ + WZ, with Z ∼ Nd(0,Σ), and W ≥ 0,
independent of Z.
2 Use the eigenvalue/Cholesky decomposition to eliminate the dependence structure.

Evaluation of Ψ−1
Distribution of ΨY belongs to the class of (centered) normal
mean-variance mixtures i.e. Y
d
=
√
WL ⋅ Z, with Z ∼ N(0,Id)
independent of W, and L ∈ Rd×d
(a Cholesky factor).
Applying an affine transformation in the integration yields (see
(Ben Hammouda et al. 2024a) for the proofs):
∫
[0,1]d
g (Ψ−1
Y (u))
ψY (Ψ−1
Y (u))
du = ∫
[0,1]d+1
g (Ψ−1
√
W
(ud+1)LΨ−1
Z (u−(d+1)))
ψY (Ψ−1
√
W
(ud+1)LΨ−1
Z (u−(d+1)))
du, (10)
with u−(d+1) denotes the vector excluding the (d + 1)-th
component.
(10) can be computed using QMC with (d + 1)-dimensional LDPs.
For the multivariate t-student distribution:
√
W follows the
inverse chi distribution with degrees of freedom ν̃.
For the multivariate Laplace distribution:
√
W follows the
Rayleigh distribution with scale 1
√
2
.
48/55

Case of Correlated Assets
1 Choose the density ψ(⋅;Λ) in the change of variable to asymptotically follow the
same functional form of the extended characteristic function.
2 Select the parameters Λ to control the growth of the integrand near the boundary
of [0,1]d
i.e limuj→0,1 g̃(uj) < ∞,j = 1,...,d.
Table 8: Choice of ψ(u;Λ) ∶= ∏
d
j=1 ψj(uj;Λ) and sufficient conditions on Λ for GBM, (ii) VG and
(iii) NIG. See (Ben Hammouda et al. 2024a) for the derivation. Kλ(y) is the modified Bessel
function of the second kind with λ = 2−d
2
, y > 0. ” ⪰ 0” ∶ denotes positive-semidefiniteness of a
matrix
Model ψ(y;Λ) Growth condition on Λ
GBM Gaussian: (2π)− d
2 (det(Σ̃))− 1
2 exp(−1
2(y′
Σ̃
−1
y)) TΣ − Σ̃
−1
⪰ 0
VG Generalized Student’s t:
Γ(ν̃+d
2
)(det(Σ̃))− 1
2
Γ(ν̃
2
)ν̃
d
2 π
d
2
(1 + 1
ν̃
(y′
Σ̃y))
− ν̃+d
2
ν̃ = 2T
ν −d, Σ−Σ̃
−1
⪰ 0
or
ν̃ ≤ 2T
ν − d, Σ̃ = Σ−1
GH Laplace: (2π)− d
2 (det(Σ̃))− 1
2 (y′Σ̃
−1
y
2 )
λ
2
Kλ (
√
2y′Σ̃
−1
y) δ2
T2
∆ − 2Σ̃
−1
⪰ 0

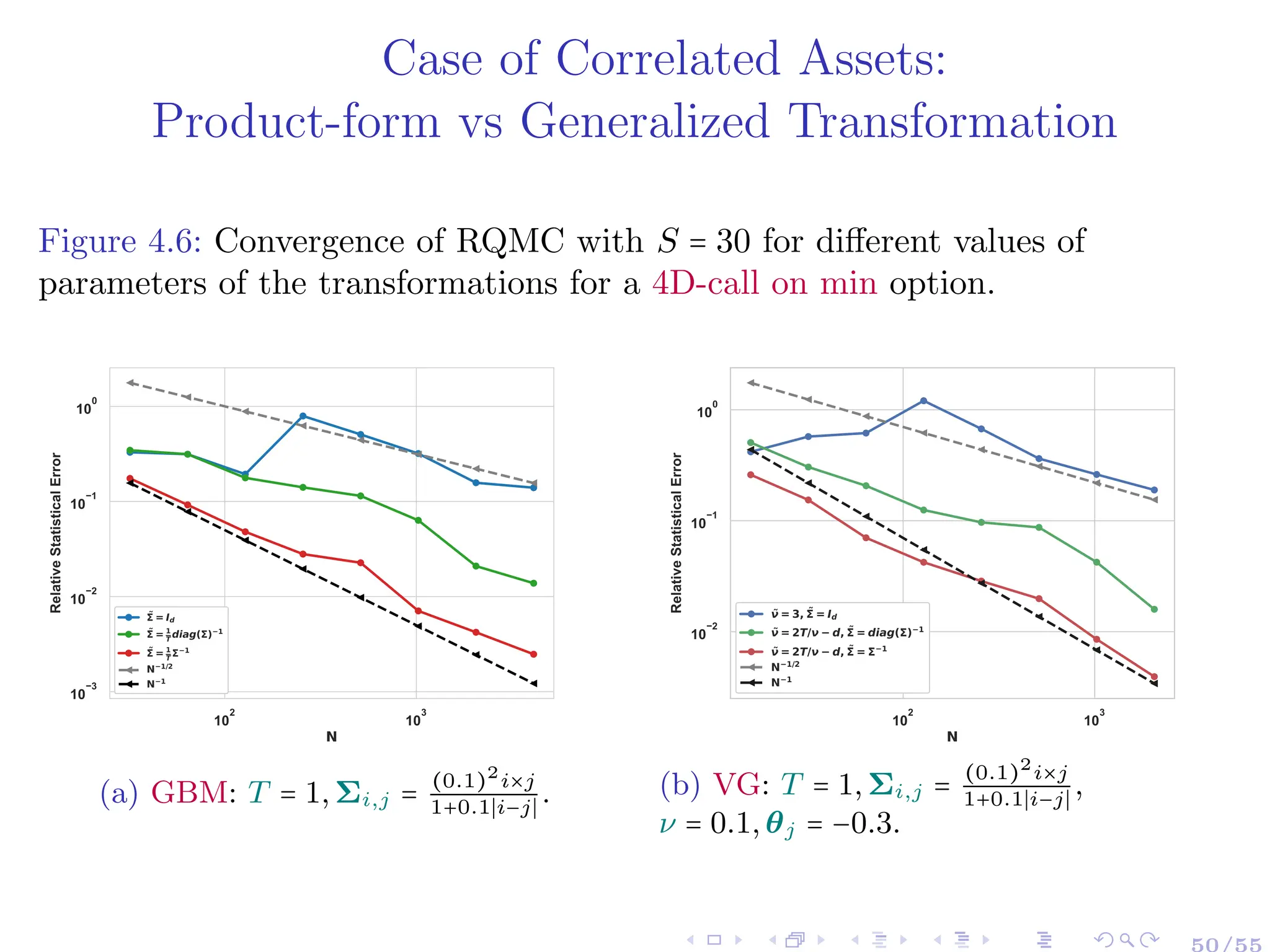
Case of Correlated Assets:
Product-form vs Generalized Transformation
Figure 4.6: Convergence of RQMC with S = 30 for different values of
parameters of the transformations for a 4D-call on min option.
10
2
10
3
N
10
−3
10
−2
10
−1
10
0
Relative
Statistical
Error
̃
Σ=Id
̃
Σ=1
Tdiag(Σ)−1
̃
Σ=1
TΣ−1
N−1/2
N−1
(a) GBM: T = 1, Σi,j = (0.1)2
i×j
1+0.1∣i−j∣
.
10
2
10
3
N
10
−2
10
−1
10
0
Relative
Statistical
Error
̃
ν =3, ̃
Σ=Id
̃
ν =2T/ν −d, ̃
Σ=diag(Σ)−1
̃
ν =2T/ν −d, ̃
Σ=Σ−1
N−1/2
N−1
(b) VG: T = 1, Σi,j = (0.1)2
i×j
1+0.1∣i−j∣
,
ν = 0.1, θj = −0.3.
50/55

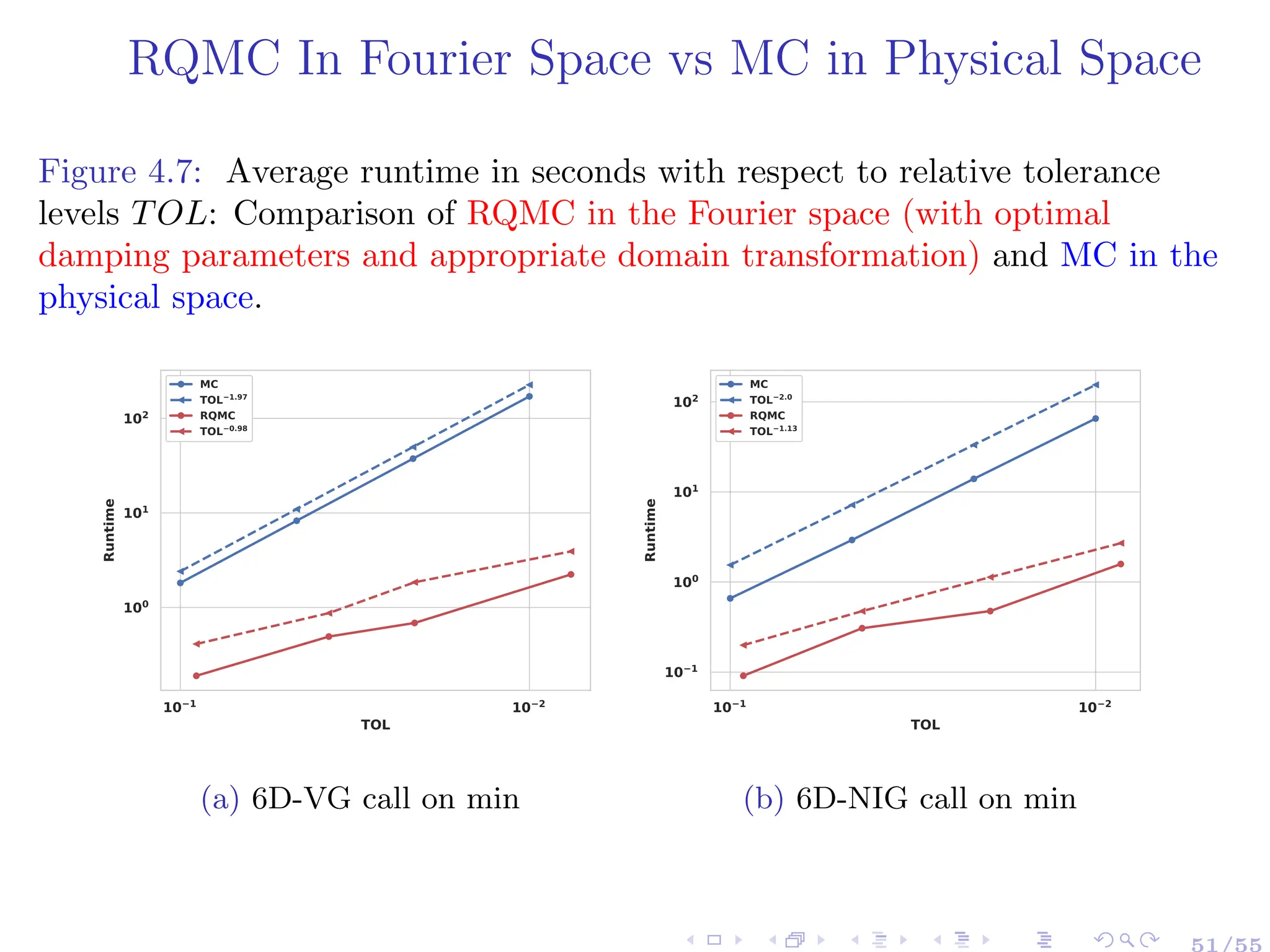
RQMC In Fourier Space vs MC in Physical Space
Figure 4.7: Average runtime in seconds with respect to relative tolerance
levels TOL: Comparison of RQMC in the Fourier space (with optimal
damping parameters and appropriate domain transformation) and MC in the
physical space.
10−2
10−1
TOL
100
101
102
Runtime
MC
TOL−1.97
RQMC
TOL−0.98
(a) 6D-VG call on min
10−2
10−1
TOL
10−1
100
101
102
Runtime
MC
TOL−2.0
RQMC
TOL−1.13
(b) 6D-NIG call on min
51/55

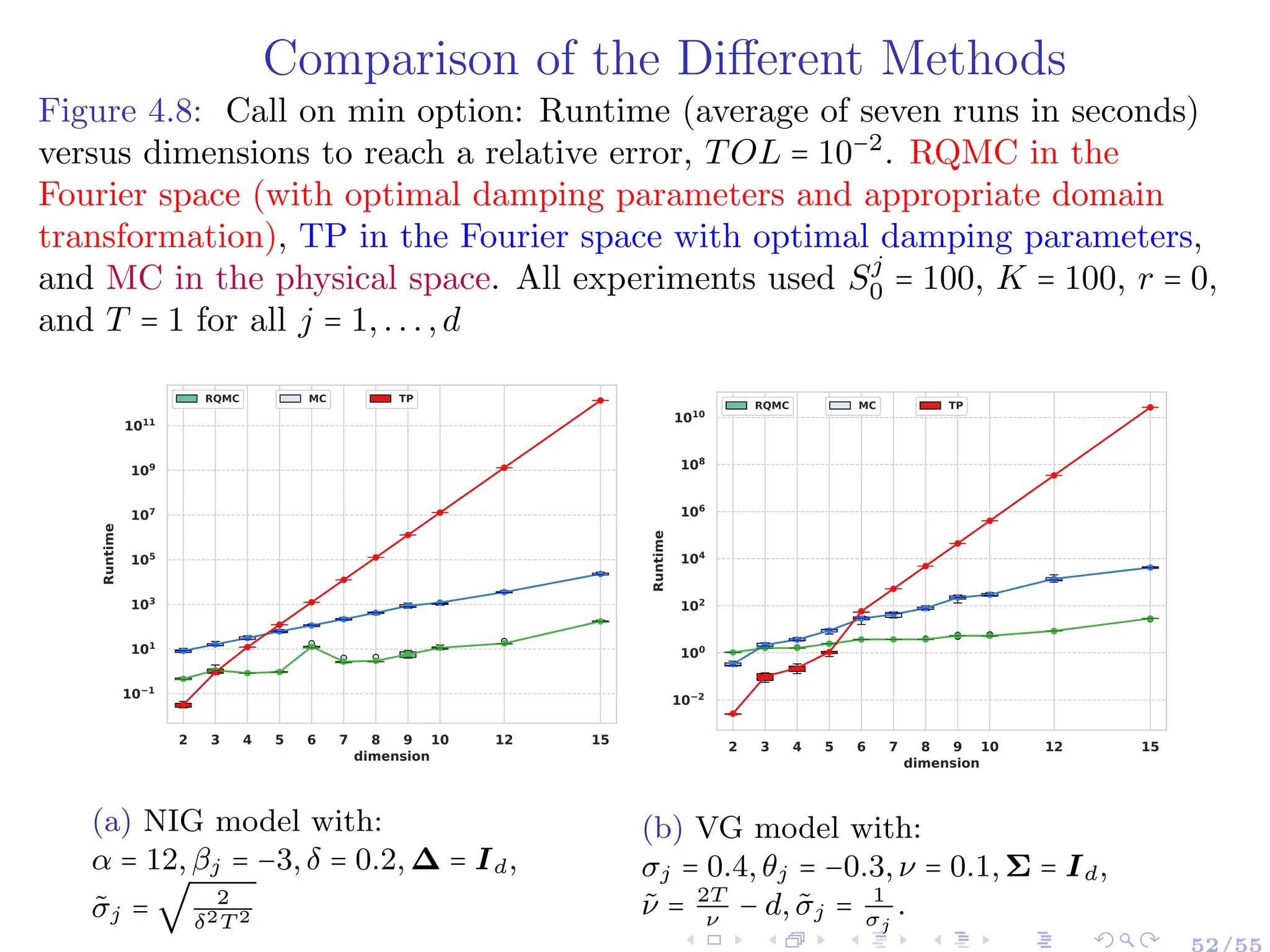
Comparison of the Different Methods
Figure 4.8: Call on min option: Runtime (average of seven runs in seconds)
versus dimensions to reach a relative error, TOL = 10−2
. RQMC in the
Fourier space (with optimal damping parameters and appropriate domain
transformation), TP in the Fourier space with optimal damping parameters,
and MC in the physical space. All experiments used Sj
0 = 100, K = 100, r = 0,
and T = 1 for all j = 1,...,d
2 3 4 5 6 7 8 9 10 12 15
dimension
10−1
101
103
105
107
109
1011
Runtime
RQMC TP
MC
MC
(a) NIG model with:
α = 12, βj = −3, δ = 0.2, ∆ = Id,
σ̃j =
√
2
δ2T 2
2 3 4 5 6 7 8 9 10 12 15
dimension
10−2
100
102
104
106
108
1010
Runtime
RQMC TP
MC
MC
(b) VG model with:
σj = 0.4, θj = −0.3, ν = 0.1, Σ = Id,
ν̃ = 2T
ν
− d, σ̃j = 1
σj
.
52/55

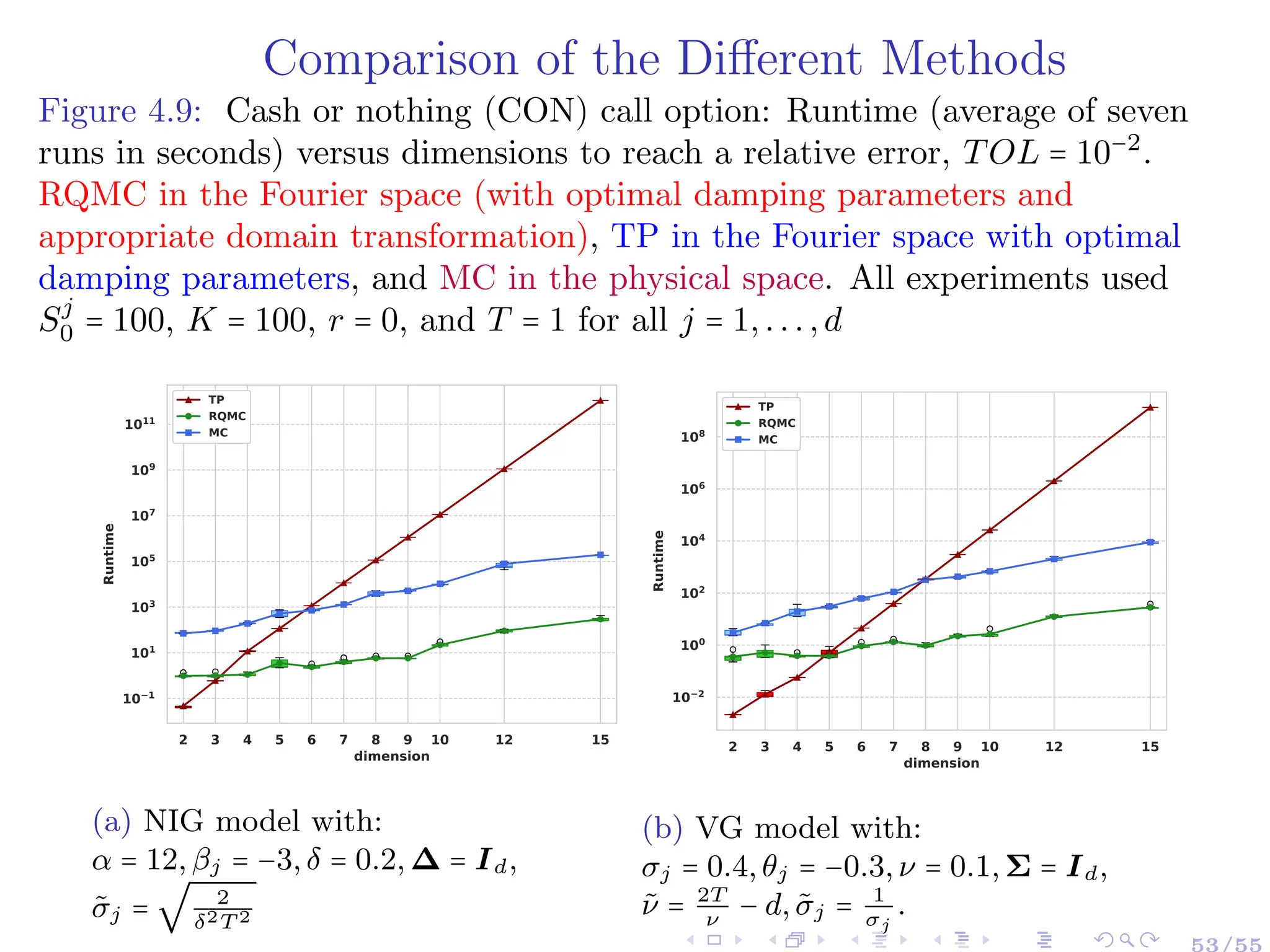
Comparison of the Different Methods
Figure 4.9: Cash or nothing (CON) call option: Runtime (average of seven
runs in seconds) versus dimensions to reach a relative error, TOL = 10−2
.
RQMC in the Fourier space (with optimal damping parameters and
appropriate domain transformation), TP in the Fourier space with optimal
damping parameters, and MC in the physical space. All experiments used
Sj
0 = 100, K = 100, r = 0, and T = 1 for all j = 1,...,d
2 3 4 5 6 7 8 9 10 12 15
dimension
10−1
101
103
105
107
109
1011
Runtime
TP
RQMC
MC
(a) NIG model with:
α = 12, βj = −3, δ = 0.2, ∆ = Id,
σ̃j =
√
2
δ2T 2
2 3 4 5 6 7 8 9 10 12 15
dimension
10−2
100
102
104
106
108
Runtime
TP
RQMC
MC
(b) VG model with:
σj = 0.4, θj = −0.3, ν = 0.1, Σ = Id,
ν̃ = 2T
ν
− d, σ̃j = 1
σj
.
53/55

5 Conclusions
53/55

Conclusion
Task (Option Pricing and Beyond): Efficiently compute:
E[g(X(T))] = ∫
Rd
g(x) ρXT
(x) dx.
The pdf, ρXT
sample from.
g(⋅) is non-smooth.
54/55

Conclusion
Task (Option Pricing and Beyond): Efficiently compute:
E[g(X(T))] = ∫
Rd
g(x) ρXT
(x) dx.
1 Uncovering the Available Hidden Regularity:
Physical space:
∫Rd g(x) ρXT
(x) dx
Fourier space:
1
(2π)d ∫Rd ̂
g(u + iR) Φ(u + iR) du
Fourier Transform
2 Parametric Smoothing:
Challenge:
Arbitrary choices for R may deteriorate
the regularity of Fourier integrand.
Solution:
(Generic) optimization rule for the choice of R
based on contour integration error estimates.
3 Addressing the Curse of Dimension:
Challenge:
Complexity of (standard) tensor
product (TP) quadrature ↗
exponentially with the dimension, d.
Solution:
▸ Sparsification and dimension-adaptivity.
▸ Quasi-Monte Carlo (QMC) with efficient domain
transformation.
54/55

Conclusion
1 The proposed damping rule significantly improves the convergence
of quadrature methods for the Fourier pricing of multi-asset
options.
2 We empower Fourier-based methods for pricing multi-asset options
(computing multivariate expectations) by employing QMC with an
appropriate domain transformation.
3 We desing a practical (model dependent) domain transformation
strategy that prevents singularities near boundaries, ensuring the
integrand retains its regularity for faster QMC convergence in the
Fourier space.
4 The designed QMC-based Fourier approach outperforms the MC
(in physical domain) and tensor product quadrature (in Fourier
space) for pricing multi-asset options across up to 15 dimensions.
5 Accompanying code can be found here:
Git repository:
Quasi-Monte-Carlo-for-Efficient-Fourier-Pricing-of-Multi-Asset-Options
55/55

Related References
Thank you for your attention!
1 C. Ben Hammouda et al. “Quasi-Monte Carlo for Efficient Fourier
Pricing of Multi-Asset Options”. In: arXiv preprint arXiv:2403.02832
(2024)
2 C. Ben Hammouda et al. “Optimal Damping with Hierarchical
Adaptive Quadrature for Efficient Fourier Pricing of Multi-Asset
Options in Lévy Models”. In: Journal of Computational Finance 27.3
(2023), pp. 43–86
3 C. Ben Hammouda et al. “Numerical smoothing with hierarchical adaptive
sparse grids and quasi-Monte Carlo methods for efficient option pricing”. In:
Quantitative Finance (2022), pp. 1–19
4 C. Ben Hammouda et al. “Multilevel Monte Carlo with numerical smoothing for
robust and efficient computation of probabilities and densities”. In: SIAM
Journal on Scientific Computing 46.3 (2024), A1514–A1548
5 C. Ben Hammouda et al. “Hierarchical adaptive sparse grids and quasi-Monte
Carlo for option pricing under the rough Bergomi model”. In: Quantitative
Finance 20.9 (2020), pp. 1457–1473
55/55

References I
[1] J.-P. Aguilar. “Some pricing tools for the Variance Gamma
model”. In: International Journal of Theoretical and Applied
Finance 23.04 (2020), p. 2050025.
[2] C. Bayer, M. Siebenmorgen, and R. Tempone. “Smoothing the
payoff for efficient computation of basket option pricing.”. In:
Quantitative Finance 18.3 (2018), pp. 491–505.
[3] C. Ben Hammouda, C. Bayer, and R. Tempone. “Hierarchical
adaptive sparse grids and quasi-Monte Carlo for option pricing
under the rough Bergomi model”. In: Quantitative Finance 20.9
(2020), pp. 1457–1473.
[4] C. Ben Hammouda, C. Bayer, and R. Tempone. “Numerical
smoothing with hierarchical adaptive sparse grids and
quasi-Monte Carlo methods for efficient option pricing”. In:
Quantitative Finance (2022), pp. 1–19.
55/55

References II
[5] C. Ben Hammouda et al. “Optimal Damping with Hierarchical
Adaptive Quadrature for Efficient Fourier Pricing of Multi-Asset
Options in Lévy Models”. In: Journal of Computational Finance
27.3 (2023), pp. 43–86.
[6] C. Ben Hammouda et al. “Quasi-Monte Carlo for Efficient
Fourier Pricing of Multi-Asset Options”. In: arXiv preprint
arXiv:2403.02832 (2024).
[7] C. Ben Hammouda, C. Bayer, and R. Tempone. “Multilevel
Monte Carlo with numerical smoothing for robust and efficient
computation of probabilities and densities”. In: SIAM Journal on
Scientific Computing 46.3 (2024), A1514–A1548.
[8] P. Carr and D. Madan. “Option valuation using the fast Fourier
transform”. In: Journal of computational finance 2.4 (1999),
pp. 61–73.
55/55

References III
[9] P. Chen. “Sparse quadrature for high-dimensional integration
with Gaussian measure”. In: ESAIM: Mathematical Modelling
and Numerical Analysis 52.2 (2018), pp. 631–657.
[10] R. Cont and P. Tankov. Financial Modelling with Jump
Processes. Chapman and Hall/CRC, 2003.
[11] P. J. Davis and P. Rabinowitz. Methods of numerical integration.
Courier Corporation, 2007.
[12] J. Dick, F. Y. Kuo, and I. H. Sloan. “High-dimensional
integration: the quasi-Monte Carlo way”. In: Acta Numerica 22
(2013), pp. 133–288.
[13] D. Duffie, D. Filipović, and W. Schachermayer. “Affine processes
and applications in finance”. In: The Annals of Applied
Probability 13.3 (2003), pp. 984–1053.
55/55

References IV
[14] E. Eberlein. “Jump–type Lévy processes”. In: Handbook of
financial time series. Springer, 2009, pp. 439–455.
[15] E. Eberlein, K. Glau, and A. Papapantoleon. “Analysis of Fourier
transform valuation formulas and applications”. In: Applied
Mathematical Finance 17.3 (2010), pp. 211–240.
[16] O. El Euch, J. Gatheral, and M. Rosenbaum. “Roughening
heston”. In: Risk (2019), pp. 84–89.
[17] O. G. Ernst, B. Sprungk, and L. Tamellini. “Convergence of
sparse collocation for functions of countably many Gaussian
random variables (with application to elliptic PDEs)”. In: SIAM
Journal on Numerical Analysis 56.2 (2018), pp. 877–905.
[18] F. Fang and C. W. Oosterlee. “A novel pricing method for
European options based on Fourier-cosine series expansions”. In:
SIAM Journal on Scientific Computing 31.2 (2009), pp. 826–848.
55/55

References V
[19] Z. He, C. Weng, and X. Wang. “Efficient computation of option
prices and Greeks by quasi–Monte Carlo method with smoothing
and dimension reduction”. In: SIAM Journal on Scientific
Computing 39.2 (2017), B298–B322.
[20] J. Healy. “The Pricing of Vanilla Options with Cash Dividends
as a Classic Vanilla Basket Option Problem”. In: arXiv preprint
arXiv:2106.12971 (2021).
[21] T. R. Hurd and Z. Zhou. “A Fourier transform method for
spread option pricing”. In: SIAM Journal on Financial
Mathematics 1.1 (2010), pp. 142–157.
[22] F. Y. Kuo, C. Schwab, and I. H. Sloan. “Quasi-Monte Carlo
methods for high-dimensional integration: the standard (weighted
Hilbert space) setting and beyond”. In: The ANZIAM Journal
53.1 (2011), pp. 1–37.
55/55

References VI
[23] F. Y. Kuo et al. “High dimensional integration of kinks and
jumps—smoothing by preintegration”. In: Journal of
Computational and Applied Mathematics 344 (2018), pp. 259–274.
[24] A. L. Lewis. “A simple option formula for general jump-diffusion
and other exponential Lévy processes”. In: Available at SSRN
282110 (2001).
[25] J. A. Nichols and F. Y. Kuo. “Fast CBC construction of
randomly shifted lattice rules achieving O (n- 1+ δ) convergence
for unbounded integrands over Rs in weighted spaces with POD
weights”. In: Journal of Complexity 30.4 (2014), pp. 444–468.
[26] D. Ouyang, X. Wang, and Z. He. “Quasi-Monte Carlo for
unbounded integrands with importance sampling”. In: arXiv
preprint arXiv:2310.00650 (2023).
55/55

References VII
[27] L. N. Trefethen. “Finite difference and spectral methods for
ordinary and partial differential equations”. In: (1996).
55/55

Empowering Fourier-based Pricing Methods for Efficient Valuation of High-Dimensional Derivatives

More Related Content

Similar to Empowering Fourier-based Pricing Methods for Efficient Valuation of High-Dimensional Derivatives

More from Chiheb Ben Hammouda

Recently uploaded

Empowering Fourier-based Pricing Methods for Efficient Valuation of High-Dimensional Derivatives