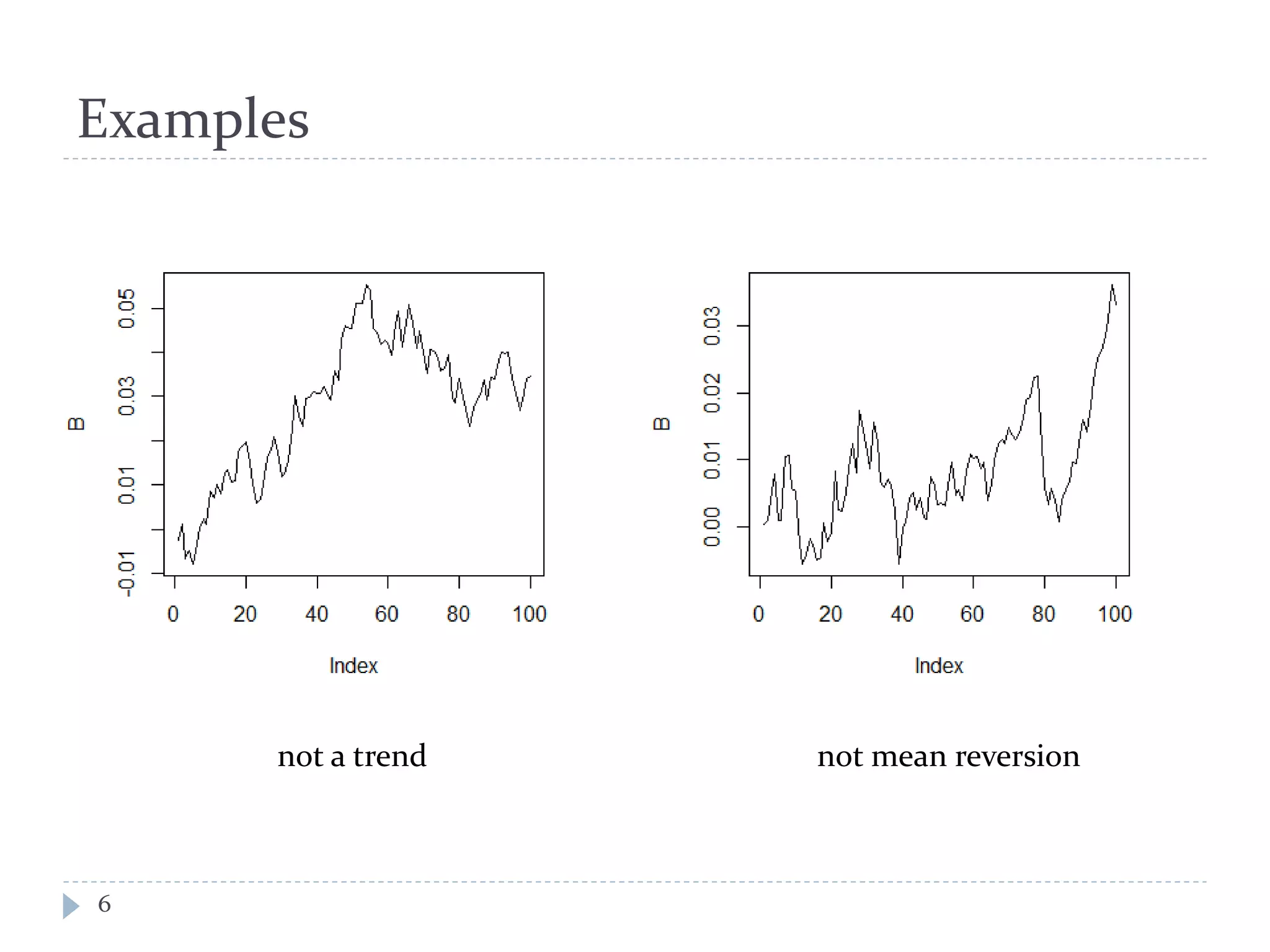
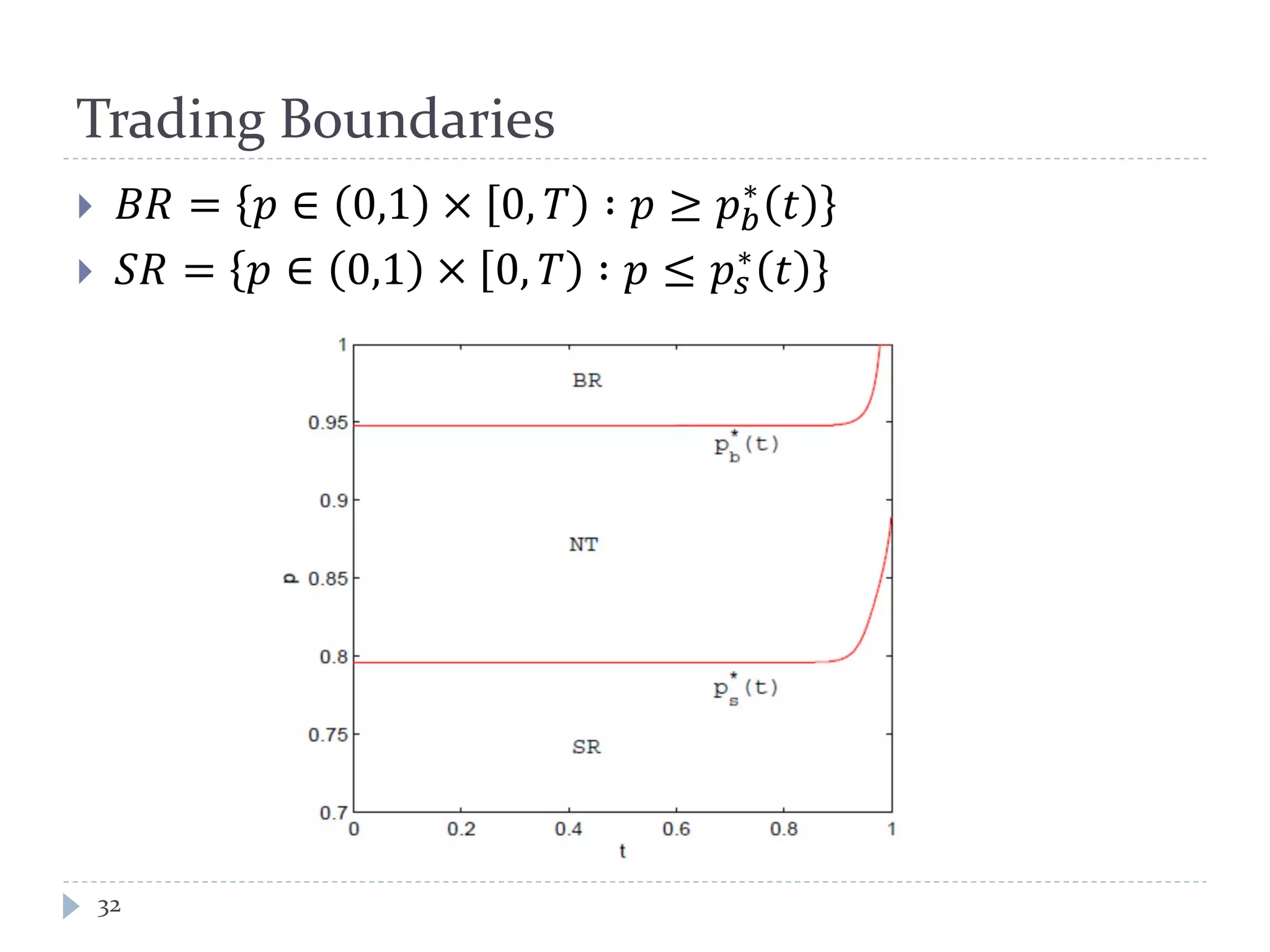
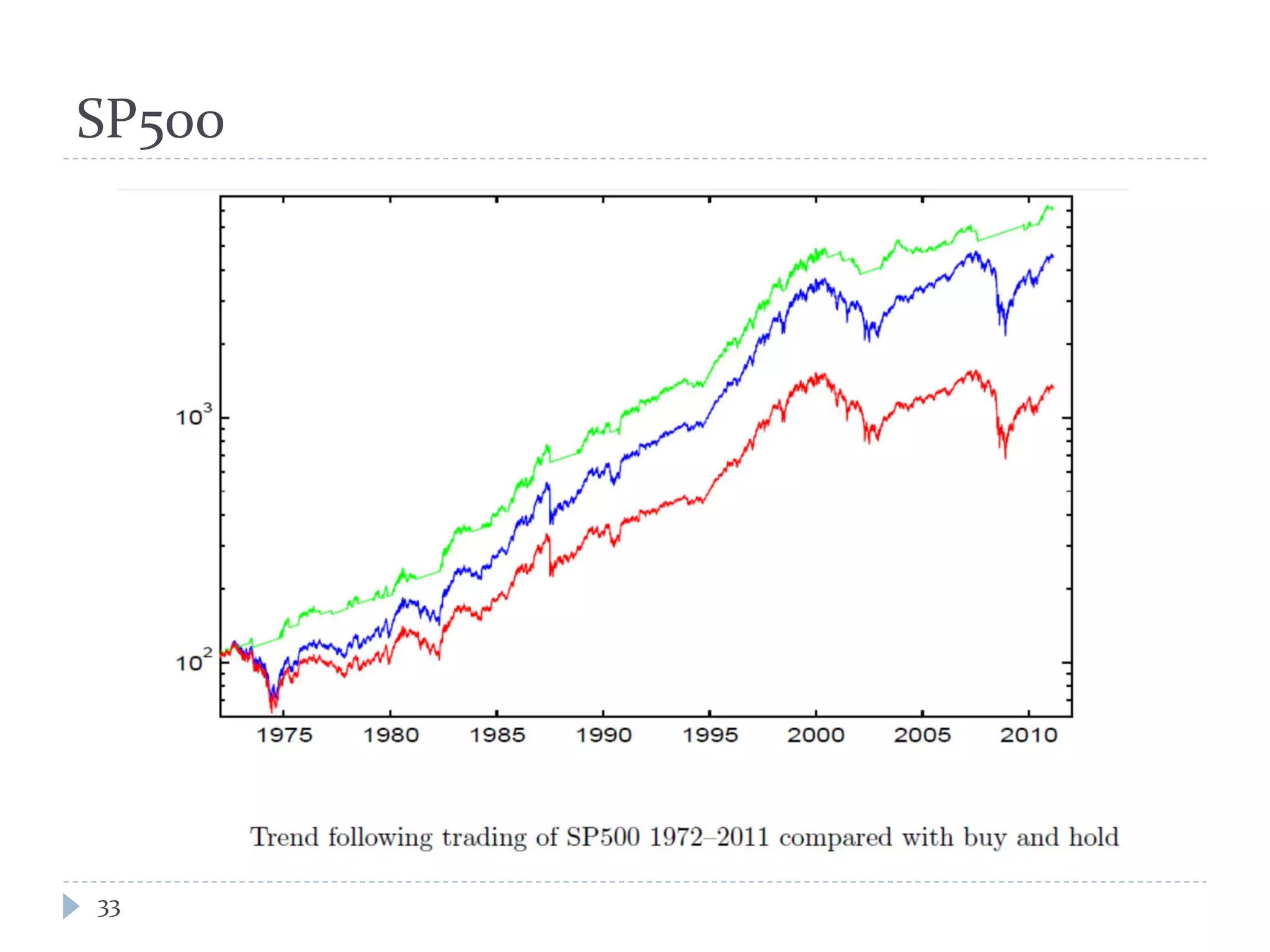
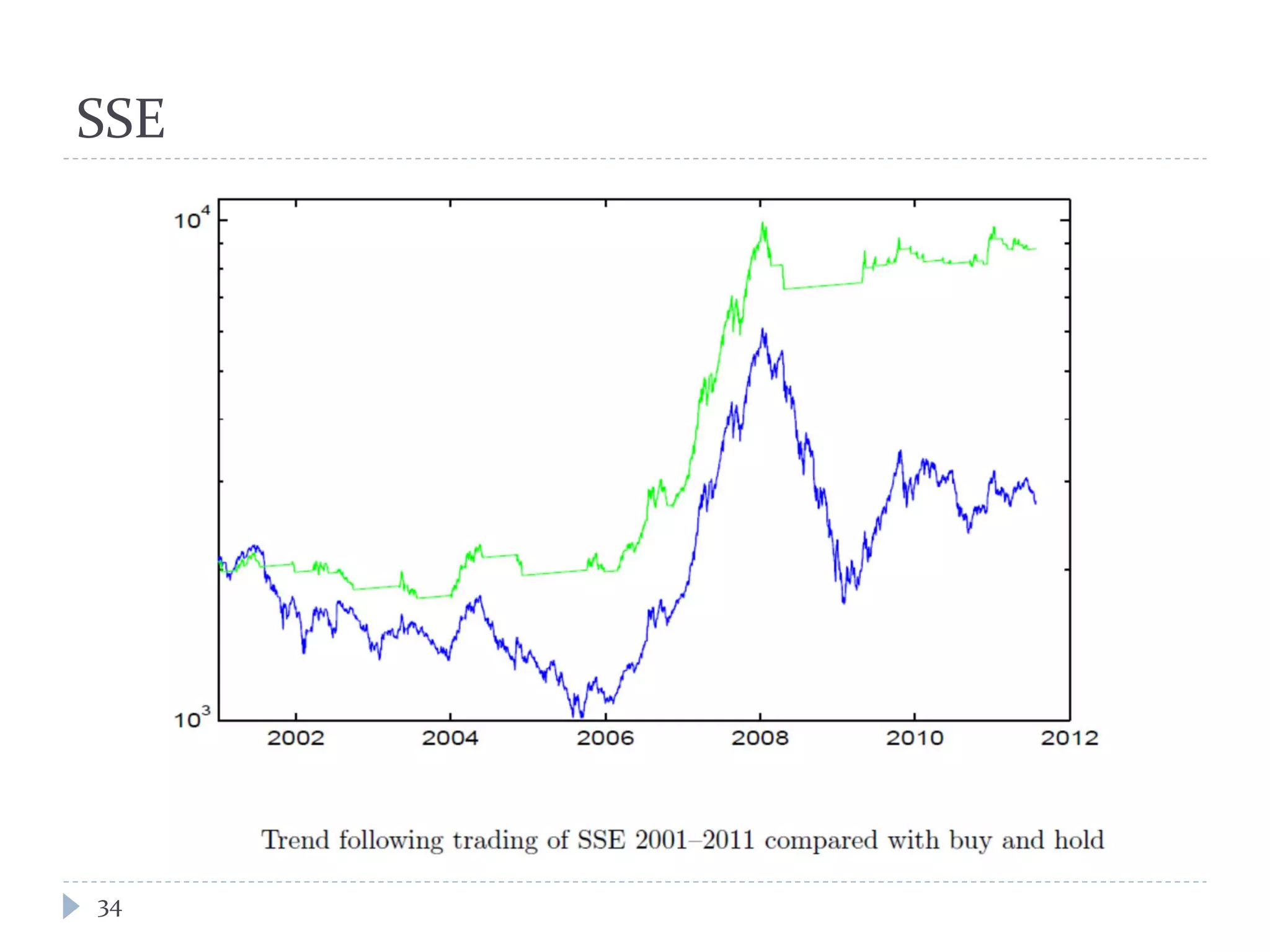
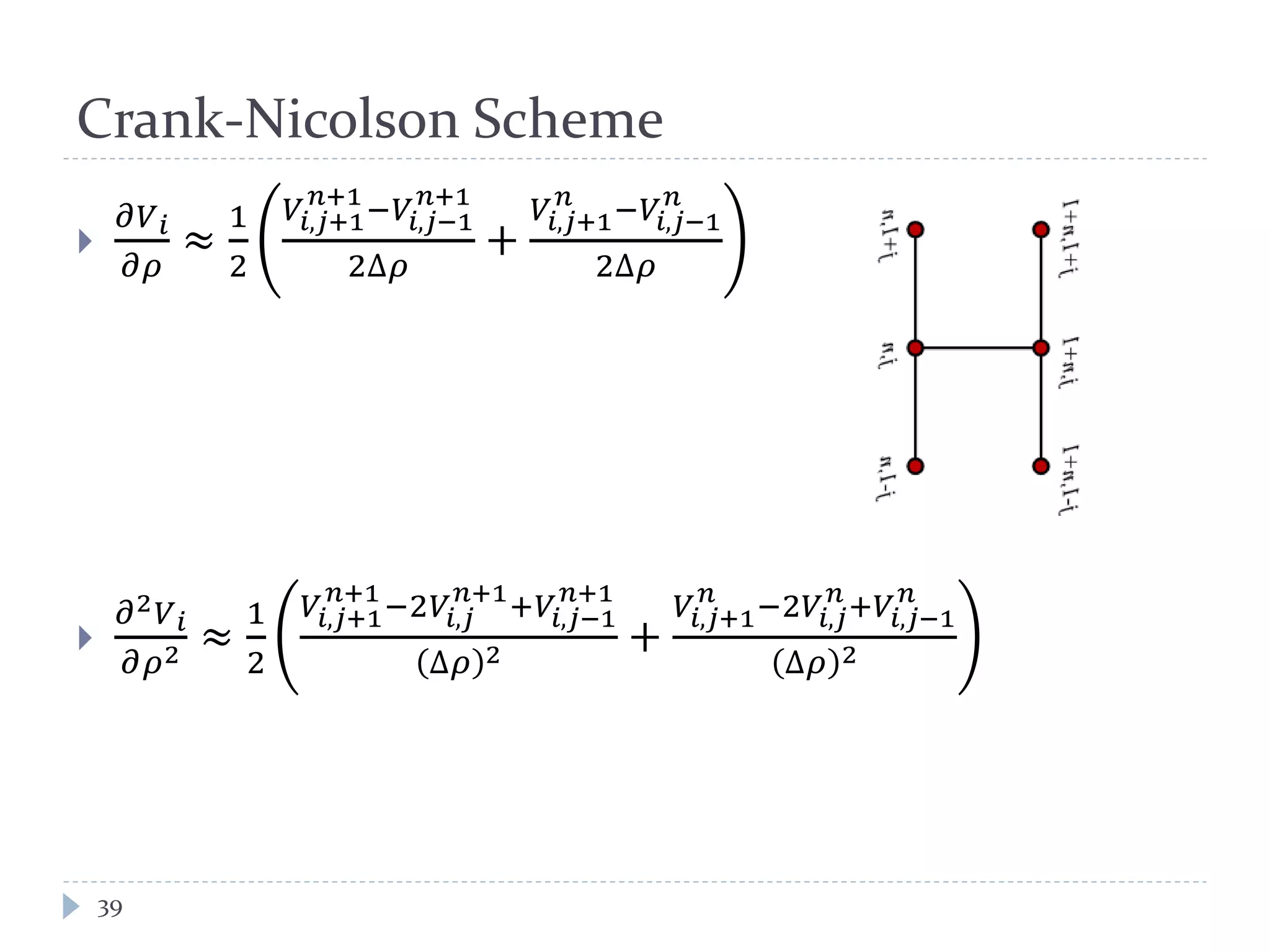
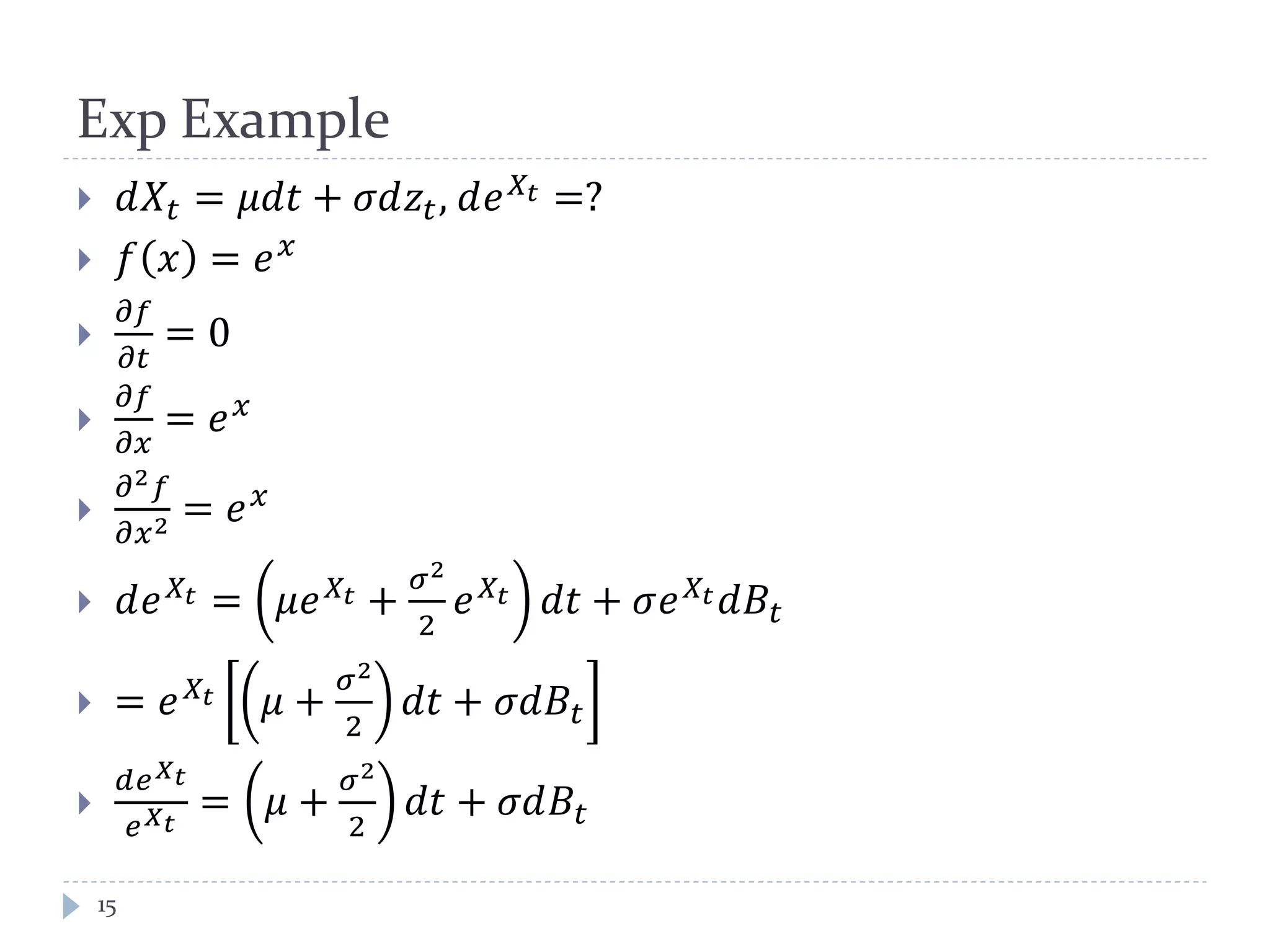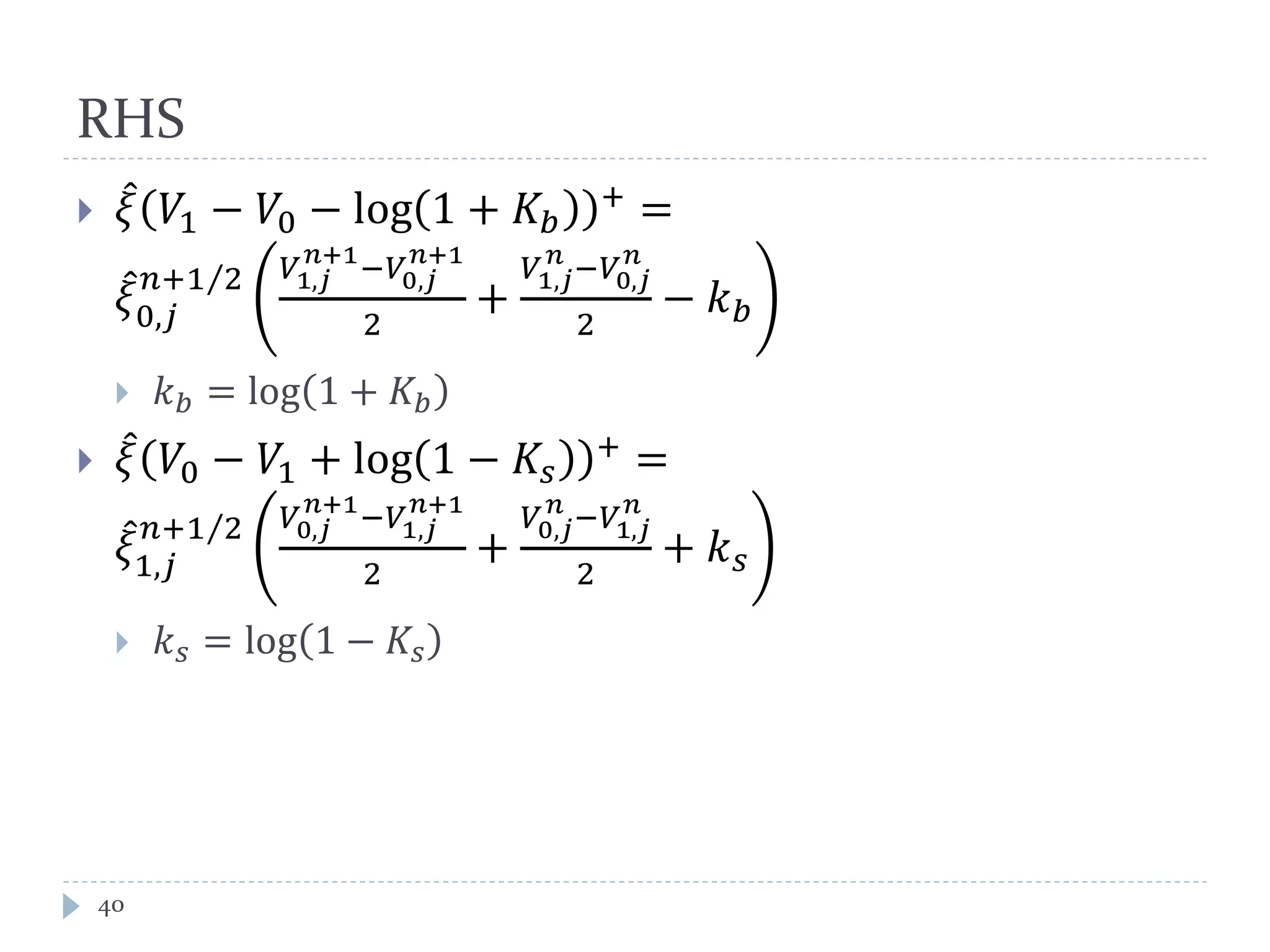AA
Uploaded byAdrian Aley
PDF, PPTX133 views

Intro to Quant Trading Strategies (Lecture 3 of 10)

This document provides an introduction to trend following strategies in algorithmic trading. It discusses Brownian motion and stochastic calculus concepts needed to model asset price movements. Geometric Brownian motion is presented as a model for asset price changes over time. Optimal trend following strategies seek to identify the optimal times to buy and sell an asset to profit from trends while minimizing transaction costs. The strategy parameters and expected returns are defined.

Embed presentation

Download as PDF, PPTX
Introduction to Algorithmic Trading Strategies Lecture 3 Trend Following Haksun Li haksun.li@numericalmethod.com www.numericalmethod.com
References 2  Introduction to Stochastic Calculus with Applications. Fima C Klebaner. 2nd Edition.  Estimating continuous time transition matrices from discretely observed data. Inamura, Yasunari. April 2006.  Optimal Trend Following Trading Rules. Dai, Min and Zhang, Qing and Zhu, Qiji Jim. 2011.
Stochastic Calculus 3
Brownian Motion 4  Independence of increments.  𝑑𝑑 = đ” 𝑡 − đ” 𝑠 is independent of any history up to 𝑠.  Normality of increments.  𝑑𝑑 is normally distributed with mean 0 and variance 𝑡 − 𝑠.  Continuity of paths.  đ” 𝑡 is a continuous function of 𝑡.
Stochastic vs. Newtonian Calculus 5  Newtonian calculus: when you zoom in a function enough, the little segment looks like a straight line, hence the approximation:  𝑑𝑑 = đ‘“Ì‡ 𝑑𝑑  Derivative exists.  The function is differentiable.  Stochastic calculus: no matter how much you zoom in or how small 𝑑𝑑 is, the function still looks very zig-zag and random. It is nothing like a straight line.  For Brownian motion, however much you zoom in, how small the segment is, it still just looks very much like a Brownian motion.  The function is therefore no where differentiable.
Examples 6 not a trend not mean reversion
dBdB 7  𝑑𝑑 2 = 𝑑𝑑𝑑𝑑 = 𝑑𝑑  ∫ đ‘‘đ”đ‘Ą 2𝑡 0 ≈ ∑ 𝑍 𝑛,𝑖 2𝑛 𝑖=1  𝑍 𝑛,𝑖 is of 𝑁 0, 𝑡 𝑛 for all 𝑖.  ∫ đ‘‘đ”đ‘Ą 2𝑡 0 ≈ sum of variances of 𝑍 𝑛,𝑖 ≈ 𝑡  Making 𝑛 → ∞ or 𝑑𝑑 → 0, we have  ∫ đ‘‘đ”đ‘Ą 2𝑡 0 = 𝑡, convergence in probability  đ‘‘đ”đ‘Ą 2 = 𝑑𝑑, in differential form  𝑑𝑑𝑑𝑡 = 0  𝑑𝑡𝑑𝑑 = 0
Asset Price Model 8  Want to model asset price movement.  Change in price = 𝑑𝑑  Change in price is not too meaningful as $1 change in a penny stock is more significant than $1 change in GOOG.  Return = 𝑑𝑑 𝑆  Model return using two parts.  Deterministic: 𝜇𝑑𝑑, the predictable part. E.g., fixed deposit interest rate.  Random/stochastic: 𝜎𝑑𝑑, where 𝜎 is the volatility of returns and đ‘‘đ” is a sample from a probability distribution, e.g., Normal.
Geometric Brownian Motion 9  Asset price: 𝑑𝑑 𝑆 = 𝜇𝜇𝜇 + đœŽđœŽđ”  đ‘‘đ”: normally distributed  E đ‘‘đ” = 0  Variance = 𝑑𝑑. It is intuitive that đ‘‘đ” should be scaled by 𝑑𝑑 otherwise the (random) return drawn would be too big from any Normal distribution for 𝑑𝑑 → 0.  đ‘‘đ” = 𝜙 𝑑𝑑, where 𝜙 is a standard Normal distribution.  Reasonably good model for stocks and indices.  Real data have more big rises and falls than this model predicts, i.e., extreme events.
GBM Properties 10  Markov property: the distribution of the next price S + 𝑑𝑑 depend only on the current price 𝑆.  E 𝑑𝑆 = E 𝜇𝑆𝑑𝑑 + đœŽđ‘†đ‘‘đ”  = E 𝜇𝜇𝜇𝜇 + E đœŽđœŽđœŽđ”  = 𝜇𝜇𝜇𝜇 + 𝜎𝜎 E đ‘‘đ”  = 𝜇𝜇𝜇𝜇  Var 𝑑𝑑 = E 𝑑𝑑2 − E 𝑑𝑑 2 = 𝜎2 𝑆2 𝑑𝑑  đ‘‘đ”đ‘‘đ‘‘ = 0  𝑑𝑑𝑑𝑑 = 0  đ‘‘đ”đ‘‘đ” = 𝑑𝑑
Stochastic Differential Equation 11  Both 𝜇 and 𝜎 can be as simple as constants, deterministic functions of 𝑡 and 𝑆, or as complicated as stochastic functions adapted to the filtration generated by 𝑆𝑡 .  𝑑𝑆𝑡 = 𝜇𝜇𝜇 + đœŽđœŽđ”đ‘Ą  𝑑𝑆𝑡 = 𝜇 𝑡, 𝑆𝑡 𝑑𝑑 + 𝜎 𝑡, 𝑆𝑡 đ‘‘đ”đ‘Ą
Univariate Ito’s Lemma 12  Assume  𝑑𝑋𝑡 = 𝜇 𝑡 𝑑𝑑 + 𝜎𝑡 đ‘‘đ”đ‘Ą  𝑓 𝑡, 𝑋𝑡 is twice differentiable of two real variables  We have  𝑑𝑑 𝑡, 𝑋𝑡 = 𝜕𝜕 𝜕𝜕 + 𝜇 𝑡 𝜕𝜕 𝜕𝜕 + 𝜎𝑡 2 2 𝜕2 𝑓 đœ•đ‘„2 𝑑𝑑 + 𝜎𝑡 𝜕𝜕 𝜕𝜕 đ‘‘đ”đ‘Ą
“Proof” 13  Taylor series  𝑑𝑓 𝑡, 𝑋  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝑑𝑋 + 1 2 𝑓𝑡𝑡 𝑑𝑑𝑑𝑑 + 𝑓𝑡𝑋 𝑑𝑑𝑑𝑋 + 𝑓𝑋𝑋 𝑑𝑋𝑑𝑡 + 𝑓𝑋𝑋 𝑑𝑑𝑑𝑋  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝑑𝑑 + 1 2 𝑓𝑋 𝑋 𝑑𝑑𝑑𝑑  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + đœŽđ‘‘đ” + 1 2 𝑓𝑋𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 2  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 + 1 2 𝑓𝑋𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 2  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 + 1 2 𝑓𝑋𝑋 𝜇2 𝑑𝑑2 + 𝜎2 đ‘‘đ”2 + 2𝜇𝑑𝑑𝜎𝑑𝑑  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 + 1 2 𝑓𝑋𝑋 𝜎2 𝑑𝑑2  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 + 1 2 𝑓𝑋𝑋 𝜎2 𝑑𝑑  = 𝑓𝑡 + 𝜇𝑓𝑋 + 1 2 𝜎2 𝑓𝑋 𝑋 𝑑𝑑 + 𝜎𝑓𝑋 𝑑𝑑
Log Example 14  For G.B.M., 𝑑𝑋𝑡 = 𝜇𝑋𝑡 𝑑𝑑 + 𝜎𝑋𝑡 𝑑𝑧𝑡, 𝑑 log 𝑋𝑡 =?  𝑓 đ‘„ = log đ‘„  𝜕𝑓 𝜕𝑡 = 0  𝜕𝑓 đœ•đ‘„ = 1 đ‘„  𝜕2 𝑓 đœ•đ‘„2 = − 1 đ‘„2  𝑑 log 𝑋𝑡 = 𝜇𝑋𝑡 1 𝑋𝑡 + 𝜎𝑋𝑡 2 2 − 1 𝑋𝑡 2 𝑑𝑑 + 𝜎𝑋𝑡 1 𝑋𝑡 đ‘‘đ”đ‘Ą  = 𝜇 − 𝜎2 2 𝑑𝑑 + đœŽđ‘‘đ”đ‘Ą
Exp Example 15  𝑑𝑋𝑡 = 𝜇𝑑𝑑 + 𝜎𝑑𝑧𝑡, 𝑑𝑒 𝑋𝑡 =?  𝑓 đ‘„ = 𝑒 đ‘„  𝜕𝑓 𝜕𝑡 = 0  𝜕𝑓 đœ•đ‘„ = 𝑒 đ‘„  𝜕2 𝑓 đœ•đ‘„2 = 𝑒 đ‘„  𝑑𝑒 𝑋𝑡 = 𝜇𝑒 𝑋𝑡 + 𝜎2 2 𝑒 𝑋𝑡 𝑑𝑑 + 𝜎𝑒 𝑋𝑡 đ‘‘đ”đ‘Ą  = 𝑒 𝑋𝑡 𝜇 + 𝜎2 2 𝑑𝑑 + đœŽđ‘‘đ”đ‘Ą  𝑑𝑒 𝑋 𝑡 𝑒 𝑋 𝑡 = 𝜇 + 𝜎2 2 𝑑𝑑 + đœŽđ‘‘đ”đ‘Ą
Stopping Time 16  A stopping time is a random time that some event is known to have occurred.  Examples:  when a stock hits a target price  when you run out of money  when a moving average crossoveroccurs  When a stock has bottomed out is NOT a stopping time because you cannot tell when it has reached its minimum without future information.
Optimal Trend Following Strategy 17
Asset Model 18  Two state Markov model for a stock’s prices: BULL and BEAR.  𝑑𝑆 𝑟 = 𝑆 𝑟 𝜇 đ›Œ 𝑟 𝑑𝑑 + đœŽđœŽđ”đ‘Ÿ , 𝑡 ≀ 𝑟 ≀ 𝑇 < ∞  The trading period is between time 𝑡, 𝑇 .  đ›Œ 𝑟 = 1,2 are the two Markov states that indicates the BULL and BEAR markets.  𝜇1 > 0  𝜇2 < 0  𝑄 = −𝜆1 𝜆1 𝜆2 −𝜆2 , the generator matrix for the Markov chain.
Generator Matrix 19  From transition matrix to generator matrix:  𝑃 𝑡, 𝑡 + Δ𝑡 = đŒ + Δ𝑡𝑡 + 𝑜 Δ𝑡  We can estimate 𝑄 by estimating 𝑃.  𝑃 𝑡, 𝑠 = 𝑃 𝑡, 𝑡 + 𝑚Δ𝑡  ≈ đŒ + Δ𝑡𝑡 𝑚 = đŒ + 𝑠−𝑡 𝑚 𝑄 𝑚 = exp 𝑠 − 𝑡 𝑄  𝑃 𝑡, 𝑡 + Δ𝑡 = exp Δ𝑡𝑡  đ‘ƒïżœ 𝑡 ≈ exp Î”đ‘Ąđ‘„ïżœ  đ‘„ïżœ ≈ 1 Δ𝑡 log đ‘ƒïżœ 𝑡  E.g., Δ𝑡 = 1 252
Optimal Stopping Times 20 t T𝜏1 𝜈1 𝜏2 𝜈2 𝜏 𝑛 𝜈 𝑛 𝑖 = 0, Λ0 = 𝜏1, 𝜈1, 𝜏2, 𝜈2, ⋯ 𝑖 = 0, Λ0 = 𝜈1, 𝜏2, 𝜈2, 𝜏3, ⋯ BUY BUY BUYSELL SELL SELL no position, bank the $ no position, bank the $ no position, bank the $ LONG LONG LONG
Parameters 21  𝜌 ≄ 0, interest free rate  𝑆𝑡 = 𝑆, the initial stock price  𝑖 = 0,1 , the net position  đŸđ‘, the transaction cost for BUYs in percentage  đŸđ‘ , the transaction cost for SELLs in percentage
Expected Return (starting flat) 22  When 𝑖 = 0,  E0,𝑡 𝑅𝑡 = E 𝑡 𝑒 𝜌 𝜏1−𝑡 ∏ 𝑆 𝜈 𝑛 𝑆 𝜏 𝑛 1âˆ’đŸđ‘  1+đŸ 𝑏 đŒ 𝜏 𝑛<𝑇 𝑒 𝜌 𝜏 𝑛+1−𝜐 𝑛∞ 𝑛=1  You are long between 𝜏 𝑛 and 𝜈 𝑛 and the return is determined by the price change discounted by the commissions.  You are flat between 𝜈 𝑛 and 𝜏 𝑛+1 and the money grows at the risk free rate.
Expected Return (starting long) 23  When 𝑖 = 1,  E1,𝑡 𝑅 𝑡 = E 𝑡 𝑆 𝜈1 𝑆 𝑒 𝜌 𝜏2−𝜈1 1 − đŸđ‘  ∏ 𝑆 𝜈 𝑛 𝑆 𝜏 𝑛 1âˆ’đŸđ‘  1+đŸ 𝑏 đŒ 𝜏 𝑛<𝑇 𝑒 𝜌 𝜏 𝑛+1−𝜐 𝑛∞ 𝑛=2  You sell the long position at 𝜈1.
Value Functions 24  It is easier to work with the log of the returns.  J0 𝑆, đ›Œ, 𝑡, Λ0 = E 𝑡 𝜌 𝜏1 − 𝑡 + ∑ log 𝑆 𝜈 𝑛 𝑆 𝜏 𝑛 + đŒ 𝜏 𝑛<𝑇 log 1âˆ’đŸđ‘  1+đŸ 𝑏 + 𝜌 𝜏 𝑛+1 − 𝜐 𝑛 ∞ 𝑛=1  J1 𝑆, đ›Œ, 𝑡, Λ1 = E 𝑡 log 𝑆 𝜈1 𝑆 + 𝜌 𝜏2 − 𝜈1 + log 1 − đŸđ‘  + ∑ log 𝑆 𝜈 𝑛 𝑆 𝜏 𝑛 + đŒ 𝜏 𝑛<𝑇 log 1âˆ’đŸđ‘  1+đŸ 𝑏 + 𝜌 𝜏 𝑛+1 − 𝜐 𝑛 ∞ 𝑛=2
Conditional Probability of Bull Market 25  𝑝 𝑟 = 𝑃 đ›Œ 𝑟 = 1 | 𝜎 𝑆 𝑱 ∶ 0 ≀ 𝑱 ≀ 𝑟  𝑝 𝑟 is therefore a random process driven by the same Brownian motion that drives 𝑆 𝑱.  𝑑𝑝 𝑟 = − 𝜆1 + 𝜆2 𝑝 𝑟 + 𝜆2 𝑑𝑑 + 𝜇1−𝜇2 𝑝 𝑟 1−𝑝 𝑟 𝜎 đ‘‘đ”đ‘Ÿ ïżœ  đ‘‘đ”đ‘Ÿ ïżœ = 𝑑 log 𝑆 𝑟 − 𝜇1−𝜇2 𝑝 𝑟+𝜇2−𝜎2 2⁄ 𝑑𝑑 𝜎  𝑝𝑡+1 = 𝑝𝑡 + 𝑔 𝑝𝑡 Δ𝑡 + 𝜇1−𝜇2 𝑝𝑡 1−𝑝𝑡 𝜎2 log 𝑆𝑡+1 𝑆𝑡  𝑔 𝑝 = − 𝜆1 + 𝜆2 𝑝 + 𝜆2 − 𝜇1−𝜇2 𝑝 1−𝑝 𝜇1−𝜇2 𝑝+𝜇2−𝜎2 2⁄ 𝜎2  Make 𝑝𝑡+1 between 0 and 1 if it falls outside the bounds.
Objective 26  Find an optimal trading sequence (the stopping times) so that the value functions are maximized.  𝑉𝑖 𝑝, 𝑡 = supΛ𝑖 đœđ‘– 𝑆, 𝑝, 𝑡, Λ 𝑖  𝑉𝑖: the maximum amount of expected returns
Realistic Expectation of Returns 27  Lower bounds:  𝑉0 𝑝, 𝑡 ≄ 𝜌 𝑇 − 𝑡  𝑉1 𝑝, 𝑡 ≄ 𝜌 𝑇 − 𝑡 + log 1 − đŸđ‘   Upper bound:  𝑉𝑖 𝑝, 𝑡 ≀ 𝜇1 − 𝜎2 2 𝑇 − 𝑡  No trading zones:  One should never buy when 𝜌 ≄ 𝜇1 − 𝜎2 2
Principal of Optimality 28  Given an optimal trading sequence, Λ 𝑖, starting from time 𝑡, the truncated sequence will also be optimal for the same trading problem starting from any stopping times 𝜏 𝑛 or 𝜐 𝑛.
Coupled Value Functions 29  ïżœ 𝑉0 𝑝, 𝑡 = sup 𝜏1 𝐾𝑡 𝜌 𝜏1 − 𝑡 − log 1 + đŸđ‘ + 𝑉1 𝑝𝜏1 , 𝜏1 𝑉1 𝑝, 𝑡 = sup 𝜈1 𝐾𝑡 log 𝑆 𝜈1 𝑆𝑡 + log 1 − đŸđ‘  + 𝑉0 𝑝 𝜈1 , 𝜈1
Hamilton-Jacobi-Bellman Equations 30  ïżœ min −ℒ𝑉0 − 𝜌, 𝑉0 − 𝑉1 + log 1 + đŸđ‘ = 0 min −ℒ𝑉1 − 𝑓 𝜌 , 𝑉1 − 𝑉0 − log 1 − đŸđ‘  = 0  with terminal conditions: ïżœ 𝑉0 𝑝, 𝑇 = 0 𝑉1 𝑝, 𝑇 = log 1 − đŸđ‘   ℒ = 𝜕𝑡 + 1 2 𝜇1−𝜇2 𝑝 1−𝑝 𝜎 2 𝜕 𝑝𝑝 + − 𝜆1 + 𝜆2 𝑝 + 𝜆2 𝜕 𝑝
Penalty Formulation Approach 31  The HJB formulation is equivalent to this system of PDEs.  ïżœ −ℒ𝑉0 − ℎ 𝜌 = đœ‰Ì‚ 𝑉1 − 𝑉0 − log 1 + đŸđ‘ + −ℒ𝑉1 − 𝑓 𝜌 = đœ‰Ì‚ 𝑉0 − 𝑉1 + log 1 − đŸđ‘  +  đœ‰Ì‚ is a penalization factor such that đœ‰Ì‚ → ∞.  ℎ 𝜌 = 𝜌
Trading Boundaries 32  đ”đ” = 𝑝 ∈ 0,1 × [0, 𝑇) ∶ 𝑝 ≄ 𝑝 𝑏 ∗ 𝑡  𝑆𝑅 = 𝑝 ∈ 0,1 × [0, 𝑇) ∶ 𝑝 ≀ 𝑝𝑠 ∗ 𝑡
SP500 33
SSE 34
Problems 35  The buy entry signals are always delayed (as expected).  The market therefore needs to bull long enough for the strategy to make profit.  If the bear market comes in too fast and hard, the exit entry may not come in soon enough.  A proper stoploss from max drawdown may help.
Finding the Boundaries 36  At any time 𝑡, we need to find 𝑝 𝑏 ∗ and 𝑝𝑠 ∗ to determine whether we buy or sell or go flat.  𝑝 𝑏 ∗ is determined by  𝑉1 𝑝 𝑏 ∗ , 𝑡 − 𝑉0 𝑝 𝑏 ∗ , 𝑡 = log 1 + đŸđ‘  𝑝𝑠 ∗ is determined by  𝑉1 𝑝𝑠 ∗, 𝑡 − 𝑉0 𝑝𝑠 ∗, 𝑡 = log 1 − đŸđ‘   Need to compute 𝑉0 𝑝, 𝑡 and 𝑉1 𝑝, 𝑡 for all 𝑝 and 𝑡.  Solve the coupled PDEs.
Discretization of ℒ 37  𝜌, 𝑡 ∈ 0,1 × [0,1)  𝜌, 𝑡 as 𝜌𝑗, 𝑡 𝑛  𝑗 ∈ 0, ⋯ , 𝑀  𝜌0 = 0  𝜌 𝑀 = 0  𝑛 ∈ 1, ⋯ , 𝑁  𝑡1 = 0  𝑡 𝑁 = 1−  𝜕𝑉 𝑖 𝜕𝑡 ≈ 𝑉𝑖,𝑗 𝑛+1 −𝑉𝑖,𝑗 𝑛 ∆𝑡
The Grid 38 𝑡1=0 𝑡1 𝑡 𝑁=1𝑡 𝑛 𝜌0=0 𝜌𝑗 𝜌 𝑀=1 𝑉𝑖 𝜌 𝑗 , 𝑡 𝑛
Crank-Nicolson Scheme 39  𝜕𝑉 𝑖 𝜕𝜌 ≈ 1 2 𝑉𝑖,𝑗+1 𝑛+1 −𝑉𝑖,𝑗−1 𝑛+1 2∆𝜌 + 𝑉𝑖,𝑗+1 𝑛 −𝑉𝑖,𝑗−1 𝑛 2∆𝜌  𝜕2 𝑉 𝑖 𝜕𝜌2 ≈ 1 2 𝑉𝑖,𝑗+1 𝑛+1 −2𝑉𝑖,𝑗 𝑛+1 +𝑉𝑖,𝑗−1 𝑛+1 ∆𝜌 2 + 𝑉𝑖,𝑗+1 𝑛 −2𝑉𝑖,𝑗 𝑛 +𝑉𝑖,𝑗−1 𝑛 ∆𝜌 2
RHS 40  đœ‰Ì‚ 𝑉1 − 𝑉0 − log 1 + đŸđ‘ + = đœ‰Ì‚ 0,𝑗 𝑛+1 2⁄ 𝑉1,𝑗 𝑛+1 −𝑉0,𝑗 𝑛+1 2 + 𝑉1,𝑗 𝑛 −𝑉0,𝑗 𝑛 2 − 𝑘 𝑏  𝑘 𝑏 = log 1 + đŸđ‘  đœ‰Ì‚ 𝑉0 − 𝑉1 + log 1 − đŸđ‘  + = đœ‰Ì‚ 1,𝑗 𝑛+1 2⁄ 𝑉0,𝑗 𝑛+1 −𝑉1,𝑗 𝑛+1 2 + 𝑉0,𝑗 𝑛 −𝑉1,𝑗 𝑛 2 + 𝑘 𝑠  𝑘 𝑠 = log 1 − đŸđ‘ 
Penalty 41  đœ‰Ì‚ 0,𝑗 𝑛+1 2⁄ = ïżœ 𝜉∆𝑡, if 𝑉1,𝑗 𝑛+1 −𝑉0,𝑗 𝑛+1 2 + 𝑉1,𝑗 𝑛 −𝑉0,𝑗 𝑛 2 − 𝑘 𝑏 > 0 0, otherwise  đœ‰Ì‚ 1,𝑗 𝑛+1 2⁄ = ïżœ 𝜉∆𝑡, if 𝑉0,𝑗 𝑛+1 −𝑉1,𝑗 𝑛+1 2 + 𝑉0,𝑗 𝑛 −𝑉1,𝑗 𝑛 2 + 𝑘 𝑠 > 0 0, otherwise
The Discretized PDEs 42  𝑎1,𝑗 𝑉0,𝑗+1 𝑛+1 + 𝑎0,𝑗 𝑉0,𝑗 𝑛+1 + 𝑎−1,𝑗 𝑉0,𝑗−1 𝑛+1 = 𝑐0,𝑗 𝑛 + đœ‰Ì‚ 0,𝑗 𝑛+1 2⁄ 𝑉1,𝑗 𝑛+1 −𝑉0,𝑗 𝑛+1 2 + 𝑉1,𝑗 𝑛 −𝑉0,𝑗 𝑛 2 − 𝑘 𝑏  𝑎1,𝑗 𝑉1,𝑗+1 𝑛+1 + 𝑎0,𝑗 𝑉1,𝑗 𝑛+1 + 𝑎−1,𝑗 𝑉1,𝑗−1 𝑛+1 = 𝑐1,𝑗 𝑛 + đœ‰Ì‚ 1,𝑗 𝑛+1 2⁄ 𝑉0,𝑗 𝑛+1 −𝑉1,𝑗 𝑛+1 2 + 𝑉0,𝑗 𝑛 −𝑉1,𝑗 𝑛 2 + 𝑘 𝑠  𝑗 ∈ 1, ⋯ , 𝑀 − 1  𝑝 = 0, 𝑝 = 1 are excluded.
The Coefficients 43  𝑎−1,𝑗 = − 1 2 𝜎 𝑝 2 ∆𝑡 2∆𝑝2 + 1 2 𝜇 𝑝 ∆𝑡 2∆𝑝  𝑎0,𝑗 = 1 + 𝜎 𝑝 2 ∆𝑡 2∆𝑝2  𝑎1,𝑗 = − 1 2 𝜎 𝑝 2 ∆𝑡 2∆𝑝2 − 1 2 𝜇 𝑝 ∆𝑡 2∆𝑝  𝑐0,𝑗 𝑛 = −𝑎1,𝑗 𝑉0,𝑗+1 𝑛 + 2 − 𝑎0,𝑗 𝑉0,𝑗 𝑛 − 𝑎−1,𝑗 𝑉0,𝑗−1 𝑛 + ℎ 𝑗∆𝑝 ∆𝑡  𝑐1,𝑗 𝑛 = −𝑎1,𝑗 𝑉1,𝑗+1 𝑛 + 2 − 𝑎0,𝑗 𝑉1,𝑗 𝑛 − 𝑎−1,𝑗 𝑉1,𝑗−1 𝑛 + 𝑓 𝑗∆𝑝 ∆𝑡
Boundary Conditions 44  𝑗 = 0, 𝑝 = 0  𝑎0,0=1  𝑎1,0 = 0  𝑐0,0 𝑛 = 𝑉0,1 𝑛 + ℎ 0 ∆𝑡  𝑐1,0 𝑛 = 𝑉1,1 𝑛 + 𝑓 0 ∆𝑡  𝑗 = 𝑀, 𝑝 = 1  𝑎0,𝑀=1  𝑎−1,𝑀 = 0  𝑐0,𝑀 𝑛 = 𝑉0,𝑀−1 𝑛 + ℎ 1 ∆𝑡  𝑐1,𝑀 𝑛 = 𝑉1,𝑀−1 𝑛 + 𝑓 1 ∆𝑡  𝑛 = 0, 𝑡 = 0, for all 𝑗 ∈ 0, ⋯ , 𝑀  𝑉0,𝑗 = 0  𝑉1,𝑗 = 𝑘 𝑠
System in Matrix Form 45  ïżœ 𝐮 𝑛 𝑉0 𝑛+1 = 𝑐⃗0 𝑛 𝐮 𝑛 𝑉1 𝑛+1 = 𝑐⃗1 𝑛  𝐮 𝑛 = 𝑎0,0 𝑎−1,1 ⋼ 0 0 0 𝑎0,1 ⋱ 
 
 0 𝑎1,1 ⋱ 𝑎−1,𝑀−1 0 
 
 ⋱ 𝑎0,𝑀−1 0 0 0 ⋼ 𝑎1,𝑀−1 𝑎0,𝑀
Solving the System of Equations 46  We already know the values of 𝑉0 0 and 𝑉1 0 .  Starting from 𝑛 = 0, using 𝐮 𝑛, we iteratively solve for 𝑉0 𝑛+1 and 𝑉1 𝑛+1 until 𝑛 = 𝑀 − 1.  There are totally M systems of equations to solve.  The equations are linear in the unknowns 𝑉0,𝑗 𝑛+1 and 𝑉1,𝑗 𝑛+1 if and only if đœ‰Ì‚ 0,𝑗 𝑛+1 2⁄ = 0.  When the equations are linear, we can use Thomas’ algorithm to solve for a tri-diagonal system of linear equations.  Otherwise, we use an iterative scheme.
Iterative Scheme 47  1st step, initialization, 𝑘 = 0  Assume đœ‰Ì‚ 𝑖,𝑗 𝑛+1 2⁄ 0 = 0. Solve for 𝑉𝑖 𝑛+1 0 .  kth step  Using 𝑉𝑖 𝑛+1 𝑘 − 1 , update đœ‰Ì‚ 𝑖,𝑗 𝑛+1 2⁄ 𝑘 .  When đœ‰Ì‚ 𝑖,𝑗 𝑛+1 2⁄ 𝑘 > 0, adjust the 𝐮 𝑛 𝑘 and 𝑐⃗𝑖 𝑛 𝑘 .  Repeat until convergence.
Adjustments (A) 48  𝐮 𝑛 𝑘 = 𝑎0,0 + 𝜉Δ𝑡 2 𝑎−1,1 ⋼ 0 0 0 𝑎0,1 + 𝜉Δ𝑡 2 ⋱ 
 
 0 𝑎1,1 ⋱ 𝑎−1,𝑀−1 0 
 
 ⋱ 𝑎0,𝑀−1 + 𝜉Δ𝑡 2 0 0 0 ⋼ 𝑎1,𝑀−1 𝑎0,𝑀 + 𝜉Δ𝑡 2
Adjustments (c) 49  𝑐⃗0 𝑛 𝑘 = 1 + 𝜉Δ𝑡 𝑉1,0 𝑛+1 𝑘−1 2 + 𝑉1,0 𝑛 −𝑉0,0 𝑛 2 − 𝑘 𝑏 𝑐0,1 𝑛 + 𝜉Δ𝑡 𝑉1,1 𝑛+1 𝑘−1 2 + 𝑉1,1 𝑛 −𝑉0,1 𝑛 2 − 𝑘 𝑏 ⋼ 𝑐0,𝑀−1 𝑛 + 𝜉Δ𝑡 𝑉1,𝑀−1 𝑛+1 𝑘−1 2 + 𝑉1,𝑀−1 𝑛 −𝑉0,𝑀−1 𝑛 2 − 𝑘 𝑏 1 + 𝜉Δ𝑡 𝑉1,𝑀 𝑛+1 𝑘−1 2 + 𝑉1,𝑀 𝑛 −𝑉0,𝑀 𝑛 2 − 𝑘 𝑏  𝑐⃗1 𝑛 𝑘 = 1 + 𝜉Δ𝑡 𝑉0,0 𝑛+1 𝑘−1 2 + 𝑉0,0 𝑛 −𝑉1,0 𝑛 2 + 𝑘 𝑠 𝑐1,1 𝑛 + 𝜉Δ𝑡 𝑉0,1 𝑛+1 𝑘−1 2 + 𝑉0,1 𝑛 −𝑉1,1 𝑛 2 + 𝑘 𝑠 ⋼ 𝑐1,𝑀−1 𝑛 + 𝜉Δ𝑡 𝑉0,𝑀−1 𝑛+1 𝑘−1 2 + 𝑉0,𝑀−1 𝑛 −𝑉1,𝑀−1 𝑛 2 + 𝑘 𝑠 1 + 𝜉Δ𝑡 𝑉0,𝑀 𝑛+1 𝑘−1 2 + 𝑉0,𝑀 𝑛 −𝑉1,𝑀 𝑛 2 + 𝑘 𝑠
Convergence 50  𝑉𝑖 𝑛+1 𝑘 𝑉𝑖 𝑛+1 𝑘−1 − 1 < 𝜀
Miscellaenous 51
Model Estimation 52  Estimate the transition probabilities in the HMM by EM.  Estimate 𝜇 and 𝜎.  The log of the prices are Gaussian.  đœŽïżœ2: sample variance  đœŽïżœ2 = 𝜎2 Δ𝑡  𝜎 = đœŽïżœ 1 Δ𝑡  đ‘šïżœ 𝑖: sample mean  đ‘šïżœ 𝑖 = 𝜇𝑖 − 𝜎2 2 Δ𝑡  𝜇𝑖 = 1 Δ𝑡 đ‘šïżœ 𝑖 + 𝜎2 2

More Related Content

PDF
Intro to Quant Trading Strategies (Lecture 8 of 10)
byAdrian Aley
 
PDF
Intro to Quant Trading Strategies (Lecture 6 of 10)
byAdrian Aley
 
PDF
Intro to Quant Trading Strategies (Lecture 7 of 10)
byAdrian Aley
 
PDF
Intro to Quant Trading Strategies (Lecture 4 of 10)
byAdrian Aley
 
PDF
Intro to Quant Trading Strategies (Lecture 1 of 10)
byAdrian Aley
 
PDF
Intro to Quant Trading Strategies (Lecture 5 of 10)
byAdrian Aley
 
PDF
Intro to Quant Trading Strategies (Lecture 9 of 10)
byAdrian Aley
 
PDF
Intro to Quant Trading Strategies (Lecture 2 of 10)
byAdrian Aley
 
Intro to Quant Trading Strategies (Lecture 8 of 10)
byAdrian Aley
 
Intro to Quant Trading Strategies (Lecture 6 of 10)
byAdrian Aley
 
Intro to Quant Trading Strategies (Lecture 7 of 10)
byAdrian Aley
 
Intro to Quant Trading Strategies (Lecture 4 of 10)
byAdrian Aley
 
Intro to Quant Trading Strategies (Lecture 1 of 10)
byAdrian Aley
 
Intro to Quant Trading Strategies (Lecture 5 of 10)
byAdrian Aley
 
Intro to Quant Trading Strategies (Lecture 9 of 10)
byAdrian Aley
 
Intro to Quant Trading Strategies (Lecture 2 of 10)
byAdrian Aley
 

What's hot

PDF
Intro to Quant Trading Strategies (Lecture 10 of 10)
byAdrian Aley
 
PDF
Intro to Quantitative Investment (Lecture 6 of 6)
byAdrian Aley
 
PDF
Intro to Quantitative Investment (Lecture 1 of 6)
byAdrian Aley
 
PDF
Intro to Quantitative Investment (Lecture 3 of 6)
byAdrian Aley
 
PDF
Discrete Probability Distributions.
byConflagratioNal Jahid
 
PPT
4 2 continuous probability distributionn
byLama K Banna
 
PPTX
Quantitative Methods for Management_MBA_Bharathiar University probability dis...
byVictor Seelan
 
PPT
Les5e ppt 04
bySubas Nandy
 
PDF
Types of Probability Distributions - Statistics II
byRupak Roy
 
PPTX
Simplex Algorithm
byAizaz Ahmad
 
PPT
Sfs4e ppt 07
byUconn Stamford
 
PDF
Bid and Ask Prices Tailored to Traders' Risk Aversion and Gain Propension: a ...
byWaqas Tariq
 
PPTX
Linear programming
byPiyush Sharma
 
PDF
Demystifying the Bias-Variance Tradeoff
byAshwin Rao
 
PPTX
Chapter 07
bybmcfad01
 
DOCX
Risk neutral probability
byHarvista Galaksi
 
PDF
The Newsvendor meets the Options Trader
byAshwin Rao
 
PPT
Simplex Method
byitsvineeth209
 
PDF
Logistic regression
byRupak Roy
 
PPT
Chapter 06
byTuul Tuul
 
Intro to Quant Trading Strategies (Lecture 10 of 10)
byAdrian Aley
 
Intro to Quantitative Investment (Lecture 6 of 6)
byAdrian Aley
 
Intro to Quantitative Investment (Lecture 1 of 6)
byAdrian Aley
 
Intro to Quantitative Investment (Lecture 3 of 6)
byAdrian Aley
 
Discrete Probability Distributions.
byConflagratioNal Jahid
 
4 2 continuous probability distributionn
byLama K Banna
 
Quantitative Methods for Management_MBA_Bharathiar University probability dis...
byVictor Seelan
 
Les5e ppt 04
bySubas Nandy
 
Types of Probability Distributions - Statistics II
byRupak Roy
 
Simplex Algorithm
byAizaz Ahmad
 
Sfs4e ppt 07
byUconn Stamford
 
Bid and Ask Prices Tailored to Traders' Risk Aversion and Gain Propension: a ...
byWaqas Tariq
 
Linear programming
byPiyush Sharma
 
Demystifying the Bias-Variance Tradeoff
byAshwin Rao
 
Chapter 07
bybmcfad01
 
Risk neutral probability
byHarvista Galaksi
 
The Newsvendor meets the Options Trader
byAshwin Rao
 
Simplex Method
byitsvineeth209
 
Logistic regression
byRupak Roy
 
Chapter 06
byTuul Tuul
 

Similar to Intro to Quant Trading Strategies (Lecture 3 of 10)

PDF
Intro to Quantitative Investment (Lecture 4 of 6)
byAdrian Aley
 
PDF
Presentation on stochastic control problem with financial applications (Merto...
byAsma Ben Slimene
 
PDF
Research internship on optimal stochastic theory with financial application u...
byAsma Ben Slimene
 
PDF
"Quantitative Trading as a Mathematical Science" by Dr. Haksun Li, Founder an...
byQuantopian
 
PPT
extreme times in finance heston model.ppt
byArounaGanou2
 
PDF
Master_Thesis_Harihara_Subramanyam_Sreenivasan
byHarihara Subramanyam Sreenivasan
 
PDF
Introduction to pairtrading
byKohta Ishikawa
 
PDF
Levy models
byMohamed Raagi
 
PDF
Scalable inference for a full multivariate stochastic volatility
bySYRTO Project
 
PPTX
13. Additional Options Topics.pptx great ppt in world
bykimwhitepig
 
PDF
Varun Balupuri - Thesis
byVarun Balupuri
 
PDF
Stochastic optimal control &amp; rl
byChoiJinwon3
 
PDF
Optimum Engineering Design - Day 2b. Classical Optimization methods
bySantiagoGarridoBulln
 
PDF
trading
bySimon Dablemont
 
PPTX
Applications of Machine Learning in High Frequency Trading
byAyan Sengupta
 
PDF
60 Years Birthday, 30 Years of Ground Breaking Innovation: A Tribute to Bruno...
byAntoine Savine
 
PDF
Empowering Fourier-based Pricing Methods for Efficient Valuation of High-Dime...
byChiheb Ben Hammouda
 
PDF
report
bySirui Zhang
 
PDF
The comparative study of finite difference method and monte carlo method for ...
byAlexander Decker
 
PDF
11.the comparative study of finite difference method and monte carlo method f...
byAlexander Decker
 
Intro to Quantitative Investment (Lecture 4 of 6)
byAdrian Aley
 
Presentation on stochastic control problem with financial applications (Merto...
byAsma Ben Slimene
 
Research internship on optimal stochastic theory with financial application u...
byAsma Ben Slimene
 
"Quantitative Trading as a Mathematical Science" by Dr. Haksun Li, Founder an...
byQuantopian
 
extreme times in finance heston model.ppt
byArounaGanou2
 
Master_Thesis_Harihara_Subramanyam_Sreenivasan
byHarihara Subramanyam Sreenivasan
 
Introduction to pairtrading
byKohta Ishikawa
 
Levy models
byMohamed Raagi
 
Scalable inference for a full multivariate stochastic volatility
bySYRTO Project
 
13. Additional Options Topics.pptx great ppt in world
bykimwhitepig
 
Varun Balupuri - Thesis
byVarun Balupuri
 
Stochastic optimal control &amp; rl
byChoiJinwon3
 
Optimum Engineering Design - Day 2b. Classical Optimization methods
bySantiagoGarridoBulln
 
trading
bySimon Dablemont
 
Applications of Machine Learning in High Frequency Trading
byAyan Sengupta
 
60 Years Birthday, 30 Years of Ground Breaking Innovation: A Tribute to Bruno...
byAntoine Savine
 
Empowering Fourier-based Pricing Methods for Efficient Valuation of High-Dime...
byChiheb Ben Hammouda
 
report
bySirui Zhang
 
The comparative study of finite difference method and monte carlo method for ...
byAlexander Decker
 
11.the comparative study of finite difference method and monte carlo method f...
byAlexander Decker
 

Recently uploaded

PDF
The Core Value of Tick Data in Quantitative Trading.pdf
byemily19980210
 
PDF
How To Convert Sidra Tokens To SDA - New Method
byTRADERS / CRYPTO SPACE đŸ’±
 
DOCX
How to buy LinkedIn accounts from us A new of it_.docx
byhi1885171
 
PPTX
Eco ch.09 SUPPLY.pptxbgskgnwngjanajsknak
byyadavjikideewani1231
 
PDF
The Complete Guide to Optimus Fintech’s Payment Reconciliation Suite - Module...
byOptimus Fintech
 
PDF
Buying Verified Cash App Accounts_ Step-by-Step Guide for 2026 .pdf
by#SEO, #usaallhub, #socialmedia, #USAaccounts, #seoservice, #Digitalmarketer
 
PDF
The Default/Foreclosure Machine - 2008 frauds missed and cover ring
byJeremy Bass
 
PDF
_How to Buy////// TikTok Seller Account.pdf
byhi1885171
 
PDF
Hungarian National Balance Engine Predict 4 different scenarios
byGåbor Nagymajtényi
 
PDF
Trade Facilitation Monitoring in Ukraine № 96
byĐ†ĐœŃŃ‚ĐžŃ‚ŃƒŃ‚ Đ”ĐșĐŸĐœĐŸĐŒŃ–Ń‡ĐœĐžŃ… ĐŽĐŸŃĐ»Ń–ĐŽĐ¶Đ”ĐœŃŒ та ĐżĐŸĐ»Ń–Ń‚ĐžŃ‡ĐœĐžŃ… ĐșĐŸĐœŃŃƒĐ»ŃŒŃ‚Đ°Ń†Ń–Đč
 
PDF
Buy LinkedIn Accounts_Best Step-by-Step Guide for 2025.pdf
bymarketing
 
PPTX
Structure of Office of the dad PCDA O.pptx
bysasdad209601
 
PPTX
Top Inventory Financing Mistakes Small Businesses Must Avoid
byAvon River Ventures
 
PDF
The $410.7 Billion Question Every CFO Needs to Answer
byPrima Consulting
 
DOCX
Understanding Twitter Accounts_ A Deep Exploration of Digital Voice, Identity...
bymarketing
 
PDF
20251203_A. Stotz All Weather Strategy - Weights update & Performance review ...
bybeamploynaphat
 
PPTX
4_Housing for Animals and resources.pptx
bybishnugup999
 
DOCX
Case Study: The Mechanics of TraderKnows Extortion
byBittam Sobrenome
 
DOCX
Case Study: The Industrialized Negative SEO & Extortion Model of TraderKnows
byQingShieldCenter
 
PDF
Anatomy of a Capture: How One Foreclosure Exposes a National Equity Machine
byJeremy Bass
 
The Core Value of Tick Data in Quantitative Trading.pdf
byemily19980210
 
How To Convert Sidra Tokens To SDA - New Method
byTRADERS / CRYPTO SPACE đŸ’±
 
How to buy LinkedIn accounts from us A new of it_.docx
byhi1885171
 
Eco ch.09 SUPPLY.pptxbgskgnwngjanajsknak
byyadavjikideewani1231
 
The Complete Guide to Optimus Fintech’s Payment Reconciliation Suite - Module...
byOptimus Fintech
 
Buying Verified Cash App Accounts_ Step-by-Step Guide for 2026 .pdf
by#SEO, #usaallhub, #socialmedia, #USAaccounts, #seoservice, #Digitalmarketer
 
The Default/Foreclosure Machine - 2008 frauds missed and cover ring
byJeremy Bass
 
_How to Buy////// TikTok Seller Account.pdf
byhi1885171
 
Hungarian National Balance Engine Predict 4 different scenarios
byGåbor Nagymajtényi
 
Trade Facilitation Monitoring in Ukraine № 96
byĐ†ĐœŃŃ‚ĐžŃ‚ŃƒŃ‚ Đ”ĐșĐŸĐœĐŸĐŒŃ–Ń‡ĐœĐžŃ… ĐŽĐŸŃĐ»Ń–ĐŽĐ¶Đ”ĐœŃŒ та ĐżĐŸĐ»Ń–Ń‚ĐžŃ‡ĐœĐžŃ… ĐșĐŸĐœŃŃƒĐ»ŃŒŃ‚Đ°Ń†Ń–Đč
 
Buy LinkedIn Accounts_Best Step-by-Step Guide for 2025.pdf
bymarketing
 
Structure of Office of the dad PCDA O.pptx
bysasdad209601
 
Top Inventory Financing Mistakes Small Businesses Must Avoid
byAvon River Ventures
 
The $410.7 Billion Question Every CFO Needs to Answer
byPrima Consulting
 
Understanding Twitter Accounts_ A Deep Exploration of Digital Voice, Identity...
bymarketing
 
20251203_A. Stotz All Weather Strategy - Weights update & Performance review ...
bybeamploynaphat
 
4_Housing for Animals and resources.pptx
bybishnugup999
 
Case Study: The Mechanics of TraderKnows Extortion
byBittam Sobrenome
 
Case Study: The Industrialized Negative SEO & Extortion Model of TraderKnows
byQingShieldCenter
 
Anatomy of a Capture: How One Foreclosure Exposes a National Equity Machine
byJeremy Bass
 

Intro to Quant Trading Strategies (Lecture 3 of 10)

  • 1.
    Introduction to AlgorithmicTrading Strategies Lecture 3 Trend Following Haksun Li haksun.li@numericalmethod.com www.numericalmethod.com
  • 2.
    References 2  Introduction toStochastic Calculus with Applications. Fima C Klebaner. 2nd Edition.  Estimating continuous time transition matrices from discretely observed data. Inamura, Yasunari. April 2006.  Optimal Trend Following Trading Rules. Dai, Min and Zhang, Qing and Zhu, Qiji Jim. 2011.
  • 3.
  • 4.
    Brownian Motion 4  Independenceof increments.  𝑑𝑑 = đ” 𝑡 − đ” 𝑠 is independent of any history up to 𝑠.  Normality of increments.  𝑑𝑑 is normally distributed with mean 0 and variance 𝑡 − 𝑠.  Continuity of paths.  đ” 𝑡 is a continuous function of 𝑡.
  • 5.
    Stochastic vs. NewtonianCalculus 5  Newtonian calculus: when you zoom in a function enough, the little segment looks like a straight line, hence the approximation:  𝑑𝑑 = đ‘“Ì‡ 𝑑𝑑  Derivative exists.  The function is differentiable.  Stochastic calculus: no matter how much you zoom in or how small 𝑑𝑑 is, the function still looks very zig-zag and random. It is nothing like a straight line.  For Brownian motion, however much you zoom in, how small the segment is, it still just looks very much like a Brownian motion.  The function is therefore no where differentiable.
  • 6.
    Examples 6 not a trendnot mean reversion
  • 7.
    dBdB 7  𝑑𝑑 2= 𝑑𝑑𝑑𝑑 = 𝑑𝑑  ∫ đ‘‘đ”đ‘Ą 2𝑡 0 ≈ ∑ 𝑍 𝑛,𝑖 2𝑛 𝑖=1  𝑍 𝑛,𝑖 is of 𝑁 0, 𝑡 𝑛 for all 𝑖.  ∫ đ‘‘đ”đ‘Ą 2𝑡 0 ≈ sum of variances of 𝑍 𝑛,𝑖 ≈ 𝑡  Making 𝑛 → ∞ or 𝑑𝑑 → 0, we have  ∫ đ‘‘đ”đ‘Ą 2𝑡 0 = 𝑡, convergence in probability  đ‘‘đ”đ‘Ą 2 = 𝑑𝑑, in differential form  𝑑𝑑𝑑𝑡 = 0  𝑑𝑡𝑑𝑑 = 0
  • 8.
    Asset Price Model 8 Want to model asset price movement.  Change in price = 𝑑𝑑  Change in price is not too meaningful as $1 change in a penny stock is more significant than $1 change in GOOG.  Return = 𝑑𝑑 𝑆  Model return using two parts.  Deterministic: 𝜇𝑑𝑑, the predictable part. E.g., fixed deposit interest rate.  Random/stochastic: 𝜎𝑑𝑑, where 𝜎 is the volatility of returns and đ‘‘đ” is a sample from a probability distribution, e.g., Normal.
  • 9.
    Geometric Brownian Motion 9 Asset price: 𝑑𝑑 𝑆 = 𝜇𝜇𝜇 + đœŽđœŽđ”  đ‘‘đ”: normally distributed  E đ‘‘đ” = 0  Variance = 𝑑𝑑. It is intuitive that đ‘‘đ” should be scaled by 𝑑𝑑 otherwise the (random) return drawn would be too big from any Normal distribution for 𝑑𝑑 → 0.  đ‘‘đ” = 𝜙 𝑑𝑑, where 𝜙 is a standard Normal distribution.  Reasonably good model for stocks and indices.  Real data have more big rises and falls than this model predicts, i.e., extreme events.
  • 10.
    GBM Properties 10  Markovproperty: the distribution of the next price S + 𝑑𝑑 depend only on the current price 𝑆.  E 𝑑𝑆 = E 𝜇𝑆𝑑𝑑 + đœŽđ‘†đ‘‘đ”  = E 𝜇𝜇𝜇𝜇 + E đœŽđœŽđœŽđ”  = 𝜇𝜇𝜇𝜇 + 𝜎𝜎 E đ‘‘đ”  = 𝜇𝜇𝜇𝜇  Var 𝑑𝑑 = E 𝑑𝑑2 − E 𝑑𝑑 2 = 𝜎2 𝑆2 𝑑𝑑  đ‘‘đ”đ‘‘đ‘‘ = 0  𝑑𝑑𝑑𝑑 = 0  đ‘‘đ”đ‘‘đ” = 𝑑𝑑
  • 11.
    Stochastic Differential Equation 11 Both 𝜇 and 𝜎 can be as simple as constants, deterministic functions of 𝑡 and 𝑆, or as complicated as stochastic functions adapted to the filtration generated by 𝑆𝑡 .  𝑑𝑆𝑡 = 𝜇𝜇𝜇 + đœŽđœŽđ”đ‘Ą  𝑑𝑆𝑡 = 𝜇 𝑡, 𝑆𝑡 𝑑𝑑 + 𝜎 𝑡, 𝑆𝑡 đ‘‘đ”đ‘Ą
  • 12.
    Univariate Ito’s Lemma 12 Assume  𝑑𝑋𝑡 = 𝜇 𝑡 𝑑𝑑 + 𝜎𝑡 đ‘‘đ”đ‘Ą  𝑓 𝑡, 𝑋𝑡 is twice differentiable of two real variables  We have  𝑑𝑑 𝑡, 𝑋𝑡 = 𝜕𝜕 𝜕𝜕 + 𝜇 𝑡 𝜕𝜕 𝜕𝜕 + 𝜎𝑡 2 2 𝜕2 𝑓 đœ•đ‘„2 𝑑𝑑 + 𝜎𝑡 𝜕𝜕 𝜕𝜕 đ‘‘đ”đ‘Ą
  • 13.
    “Proof” 13  Taylor series ïœđ‘‘đ‘“ 𝑡, 𝑋  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝑑𝑋 + 1 2 𝑓𝑡𝑡 𝑑𝑑𝑑𝑑 + 𝑓𝑡𝑋 𝑑𝑑𝑑𝑋 + 𝑓𝑋𝑋 𝑑𝑋𝑑𝑡 + 𝑓𝑋𝑋 𝑑𝑑𝑑𝑋  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝑑𝑑 + 1 2 𝑓𝑋 𝑋 𝑑𝑑𝑑𝑑  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + đœŽđ‘‘đ” + 1 2 𝑓𝑋𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 2  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 + 1 2 𝑓𝑋𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 2  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 + 1 2 𝑓𝑋𝑋 𝜇2 𝑑𝑑2 + 𝜎2 đ‘‘đ”2 + 2𝜇𝑑𝑑𝜎𝑑𝑑  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 + 1 2 𝑓𝑋𝑋 𝜎2 𝑑𝑑2  = 𝑓𝑡 𝑑𝑑 + 𝑓𝑋 𝜇𝑑𝑑 + 𝜎𝑑𝑑 + 1 2 𝑓𝑋𝑋 𝜎2 𝑑𝑑  = 𝑓𝑡 + 𝜇𝑓𝑋 + 1 2 𝜎2 𝑓𝑋 𝑋 𝑑𝑑 + 𝜎𝑓𝑋 𝑑𝑑
  • 14.
    Log Example 14  ForG.B.M., 𝑑𝑋𝑡 = 𝜇𝑋𝑡 𝑑𝑑 + 𝜎𝑋𝑡 𝑑𝑧𝑡, 𝑑 log 𝑋𝑡 =?  𝑓 đ‘„ = log đ‘„  𝜕𝑓 𝜕𝑡 = 0  𝜕𝑓 đœ•đ‘„ = 1 đ‘„  𝜕2 𝑓 đœ•đ‘„2 = − 1 đ‘„2  𝑑 log 𝑋𝑡 = 𝜇𝑋𝑡 1 𝑋𝑡 + 𝜎𝑋𝑡 2 2 − 1 𝑋𝑡 2 𝑑𝑑 + 𝜎𝑋𝑡 1 𝑋𝑡 đ‘‘đ”đ‘Ą  = 𝜇 − 𝜎2 2 𝑑𝑑 + đœŽđ‘‘đ”đ‘Ą
  • 15.
    Exp Example 15  𝑑𝑋𝑡= 𝜇𝑑𝑑 + 𝜎𝑑𝑧𝑡, 𝑑𝑒 𝑋𝑡 =?  𝑓 đ‘„ = 𝑒 đ‘„  𝜕𝑓 𝜕𝑡 = 0  𝜕𝑓 đœ•đ‘„ = 𝑒 đ‘„  𝜕2 𝑓 đœ•đ‘„2 = 𝑒 đ‘„  𝑑𝑒 𝑋𝑡 = 𝜇𝑒 𝑋𝑡 + 𝜎2 2 𝑒 𝑋𝑡 𝑑𝑑 + 𝜎𝑒 𝑋𝑡 đ‘‘đ”đ‘Ą  = 𝑒 𝑋𝑡 𝜇 + 𝜎2 2 𝑑𝑑 + đœŽđ‘‘đ”đ‘Ą  𝑑𝑒 𝑋 𝑡 𝑒 𝑋 𝑡 = 𝜇 + 𝜎2 2 𝑑𝑑 + đœŽđ‘‘đ”đ‘Ą
  • 16.
    Stopping Time 16  Astopping time is a random time that some event is known to have occurred.  Examples:  when a stock hits a target price  when you run out of money  when a moving average crossoveroccurs  When a stock has bottomed out is NOT a stopping time because you cannot tell when it has reached its minimum without future information.
  • 17.
  • 18.
    Asset Model 18  Twostate Markov model for a stock’s prices: BULL and BEAR.  𝑑𝑆 𝑟 = 𝑆 𝑟 𝜇 đ›Œ 𝑟 𝑑𝑑 + đœŽđœŽđ”đ‘Ÿ , 𝑡 ≀ 𝑟 ≀ 𝑇 < ∞  The trading period is between time 𝑡, 𝑇 .  đ›Œ 𝑟 = 1,2 are the two Markov states that indicates the BULL and BEAR markets.  𝜇1 > 0  𝜇2 < 0  𝑄 = −𝜆1 𝜆1 𝜆2 −𝜆2 , the generator matrix for the Markov chain.
  • 19.
    Generator Matrix 19  Fromtransition matrix to generator matrix:  𝑃 𝑡, 𝑡 + Δ𝑡 = đŒ + Δ𝑡𝑡 + 𝑜 Δ𝑡  We can estimate 𝑄 by estimating 𝑃.  𝑃 𝑡, 𝑠 = 𝑃 𝑡, 𝑡 + 𝑚Δ𝑡  ≈ đŒ + Δ𝑡𝑡 𝑚 = đŒ + 𝑠−𝑡 𝑚 𝑄 𝑚 = exp 𝑠 − 𝑡 𝑄  𝑃 𝑡, 𝑡 + Δ𝑡 = exp Δ𝑡𝑡  đ‘ƒïżœ 𝑡 ≈ exp Î”đ‘Ąđ‘„ïżœ  đ‘„ïżœ ≈ 1 Δ𝑡 log đ‘ƒïżœ 𝑡  E.g., Δ𝑡 = 1 252
  • 20.
    Optimal Stopping Times 20 tT𝜏1 𝜈1 𝜏2 𝜈2 𝜏 𝑛 𝜈 𝑛 𝑖 = 0, Λ0 = 𝜏1, 𝜈1, 𝜏2, 𝜈2, ⋯ 𝑖 = 0, Λ0 = 𝜈1, 𝜏2, 𝜈2, 𝜏3, ⋯ BUY BUY BUYSELL SELL SELL no position, bank the $ no position, bank the $ no position, bank the $ LONG LONG LONG
  • 21.
    Parameters 21  𝜌 ≄0, interest free rate  𝑆𝑡 = 𝑆, the initial stock price  𝑖 = 0,1 , the net position  đŸđ‘, the transaction cost for BUYs in percentage  đŸđ‘ , the transaction cost for SELLs in percentage
  • 22.
    Expected Return (startingflat) 22  When 𝑖 = 0,  E0,𝑡 𝑅𝑡 = E 𝑡 𝑒 𝜌 𝜏1−𝑡 ∏ 𝑆 𝜈 𝑛 𝑆 𝜏 𝑛 1âˆ’đŸđ‘  1+đŸ 𝑏 đŒ 𝜏 𝑛<𝑇 𝑒 𝜌 𝜏 𝑛+1−𝜐 𝑛∞ 𝑛=1  You are long between 𝜏 𝑛 and 𝜈 𝑛 and the return is determined by the price change discounted by the commissions.  You are flat between 𝜈 𝑛 and 𝜏 𝑛+1 and the money grows at the risk free rate.
  • 23.
    Expected Return (startinglong) 23  When 𝑖 = 1,  E1,𝑡 𝑅 𝑡 = E 𝑡 𝑆 𝜈1 𝑆 𝑒 𝜌 𝜏2−𝜈1 1 − đŸđ‘  ∏ 𝑆 𝜈 𝑛 𝑆 𝜏 𝑛 1âˆ’đŸđ‘  1+đŸ 𝑏 đŒ 𝜏 𝑛<𝑇 𝑒 𝜌 𝜏 𝑛+1−𝜐 𝑛∞ 𝑛=2  You sell the long position at 𝜈1.
  • 24.
    Value Functions 24  Itis easier to work with the log of the returns.  J0 𝑆, đ›Œ, 𝑡, Λ0 = E 𝑡 𝜌 𝜏1 − 𝑡 + ∑ log 𝑆 𝜈 𝑛 𝑆 𝜏 𝑛 + đŒ 𝜏 𝑛<𝑇 log 1âˆ’đŸđ‘  1+đŸ 𝑏 + 𝜌 𝜏 𝑛+1 − 𝜐 𝑛 ∞ 𝑛=1  J1 𝑆, đ›Œ, 𝑡, Λ1 = E 𝑡 log 𝑆 𝜈1 𝑆 + 𝜌 𝜏2 − 𝜈1 + log 1 − đŸđ‘  + ∑ log 𝑆 𝜈 𝑛 𝑆 𝜏 𝑛 + đŒ 𝜏 𝑛<𝑇 log 1âˆ’đŸđ‘  1+đŸ 𝑏 + 𝜌 𝜏 𝑛+1 − 𝜐 𝑛 ∞ 𝑛=2
  • 25.
    Conditional Probability ofBull Market 25  𝑝 𝑟 = 𝑃 đ›Œ 𝑟 = 1 | 𝜎 𝑆 𝑱 ∶ 0 ≀ 𝑱 ≀ 𝑟  𝑝 𝑟 is therefore a random process driven by the same Brownian motion that drives 𝑆 𝑱.  𝑑𝑝 𝑟 = − 𝜆1 + 𝜆2 𝑝 𝑟 + 𝜆2 𝑑𝑑 + 𝜇1−𝜇2 𝑝 𝑟 1−𝑝 𝑟 𝜎 đ‘‘đ”đ‘Ÿ ïżœ  đ‘‘đ”đ‘Ÿ ïżœ = 𝑑 log 𝑆 𝑟 − 𝜇1−𝜇2 𝑝 𝑟+𝜇2−𝜎2 2⁄ 𝑑𝑑 𝜎  𝑝𝑡+1 = 𝑝𝑡 + 𝑔 𝑝𝑡 Δ𝑡 + 𝜇1−𝜇2 𝑝𝑡 1−𝑝𝑡 𝜎2 log 𝑆𝑡+1 𝑆𝑡  𝑔 𝑝 = − 𝜆1 + 𝜆2 𝑝 + 𝜆2 − 𝜇1−𝜇2 𝑝 1−𝑝 𝜇1−𝜇2 𝑝+𝜇2−𝜎2 2⁄ 𝜎2  Make 𝑝𝑡+1 between 0 and 1 if it falls outside the bounds.
  • 26.
    Objective 26  Find anoptimal trading sequence (the stopping times) so that the value functions are maximized.  𝑉𝑖 𝑝, 𝑡 = supΛ𝑖 đœđ‘– 𝑆, 𝑝, 𝑡, Λ 𝑖  𝑉𝑖: the maximum amount of expected returns
  • 27.
    Realistic Expectation ofReturns 27  Lower bounds:  𝑉0 𝑝, 𝑡 ≄ 𝜌 𝑇 − 𝑡  𝑉1 𝑝, 𝑡 ≄ 𝜌 𝑇 − 𝑡 + log 1 − đŸđ‘   Upper bound:  𝑉𝑖 𝑝, 𝑡 ≀ 𝜇1 − 𝜎2 2 𝑇 − 𝑡  No trading zones:  One should never buy when 𝜌 ≄ 𝜇1 − 𝜎2 2
  • 28.
    Principal of Optimality 28 Given an optimal trading sequence, Λ 𝑖, starting from time 𝑡, the truncated sequence will also be optimal for the same trading problem starting from any stopping times 𝜏 𝑛 or 𝜐 𝑛.
  • 29.
    Coupled Value Functions 29 ïœïżœ 𝑉0 𝑝, 𝑡 = sup 𝜏1 𝐾𝑡 𝜌 𝜏1 − 𝑡 − log 1 + đŸđ‘ + 𝑉1 𝑝𝜏1 , 𝜏1 𝑉1 𝑝, 𝑡 = sup 𝜈1 𝐾𝑡 log 𝑆 𝜈1 𝑆𝑡 + log 1 − đŸđ‘  + 𝑉0 𝑝 𝜈1 , 𝜈1
  • 30.
    Hamilton-Jacobi-Bellman Equations 30  ïżœ min−ℒ𝑉0 − 𝜌, 𝑉0 − 𝑉1 + log 1 + đŸđ‘ = 0 min −ℒ𝑉1 − 𝑓 𝜌 , 𝑉1 − 𝑉0 − log 1 − đŸđ‘  = 0  with terminal conditions: ïżœ 𝑉0 𝑝, 𝑇 = 0 𝑉1 𝑝, 𝑇 = log 1 − đŸđ‘   ℒ = 𝜕𝑡 + 1 2 𝜇1−𝜇2 𝑝 1−𝑝 𝜎 2 𝜕 𝑝𝑝 + − 𝜆1 + 𝜆2 𝑝 + 𝜆2 𝜕 𝑝
  • 31.
    Penalty Formulation Approach 31 The HJB formulation is equivalent to this system of PDEs.  ïżœ −ℒ𝑉0 − ℎ 𝜌 = đœ‰Ì‚ 𝑉1 − 𝑉0 − log 1 + đŸđ‘ + −ℒ𝑉1 − 𝑓 𝜌 = đœ‰Ì‚ 𝑉0 − 𝑉1 + log 1 − đŸđ‘  +  đœ‰Ì‚ is a penalization factor such that đœ‰Ì‚ → ∞.  ℎ 𝜌 = 𝜌
  • 32.
    Trading Boundaries 32  đ”đ”= 𝑝 ∈ 0,1 × [0, 𝑇) ∶ 𝑝 ≄ 𝑝 𝑏 ∗ 𝑡  𝑆𝑅 = 𝑝 ∈ 0,1 × [0, 𝑇) ∶ 𝑝 ≀ 𝑝𝑠 ∗ 𝑡
  • 33.
  • 34.
  • 35.
    Problems 35  The buyentry signals are always delayed (as expected).  The market therefore needs to bull long enough for the strategy to make profit.  If the bear market comes in too fast and hard, the exit entry may not come in soon enough.  A proper stoploss from max drawdown may help.
  • 36.
    Finding the Boundaries 36 At any time 𝑡, we need to find 𝑝 𝑏 ∗ and 𝑝𝑠 ∗ to determine whether we buy or sell or go flat.  𝑝 𝑏 ∗ is determined by  𝑉1 𝑝 𝑏 ∗ , 𝑡 − 𝑉0 𝑝 𝑏 ∗ , 𝑡 = log 1 + đŸđ‘  𝑝𝑠 ∗ is determined by  𝑉1 𝑝𝑠 ∗, 𝑡 − 𝑉0 𝑝𝑠 ∗, 𝑡 = log 1 − đŸđ‘   Need to compute 𝑉0 𝑝, 𝑡 and 𝑉1 𝑝, 𝑡 for all 𝑝 and 𝑡.  Solve the coupled PDEs.
  • 37.
    Discretization of ℒ 37 ïœđœŒ, 𝑡 ∈ 0,1 × [0,1)  𝜌, 𝑡 as 𝜌𝑗, 𝑡 𝑛  𝑗 ∈ 0, ⋯ , 𝑀  𝜌0 = 0  𝜌 𝑀 = 0  𝑛 ∈ 1, ⋯ , 𝑁  𝑡1 = 0  𝑡 𝑁 = 1−  𝜕𝑉 𝑖 𝜕𝑡 ≈ 𝑉𝑖,𝑗 𝑛+1 −𝑉𝑖,𝑗 𝑛 ∆𝑡
  • 38.
    The Grid 38 𝑡1=0 𝑡1𝑡 𝑁=1𝑡 𝑛 𝜌0=0 𝜌𝑗 𝜌 𝑀=1 𝑉𝑖 𝜌 𝑗 , 𝑡 𝑛
  • 39.
    Crank-Nicolson Scheme 39  𝜕𝑉 𝑖 𝜕𝜌 ≈ 1 2 𝑉𝑖,𝑗+1 𝑛+1 −𝑉𝑖,𝑗−1 𝑛+1 2∆𝜌 + 𝑉𝑖,𝑗+1 𝑛 −𝑉𝑖,𝑗−1 𝑛 2∆𝜌  𝜕2𝑉 𝑖 𝜕𝜌2 ≈ 1 2 𝑉𝑖,𝑗+1 𝑛+1 −2𝑉𝑖,𝑗 𝑛+1 +𝑉𝑖,𝑗−1 𝑛+1 ∆𝜌 2 + 𝑉𝑖,𝑗+1 𝑛 −2𝑉𝑖,𝑗 𝑛 +𝑉𝑖,𝑗−1 𝑛 ∆𝜌 2
  • 40.
    RHS 40  đœ‰Ì‚ 𝑉1− 𝑉0 − log 1 + đŸđ‘ + = đœ‰Ì‚ 0,𝑗 𝑛+1 2⁄ 𝑉1,𝑗 𝑛+1 −𝑉0,𝑗 𝑛+1 2 + 𝑉1,𝑗 𝑛 −𝑉0,𝑗 𝑛 2 − 𝑘 𝑏  𝑘 𝑏 = log 1 + đŸđ‘  đœ‰Ì‚ 𝑉0 − 𝑉1 + log 1 − đŸđ‘  + = đœ‰Ì‚ 1,𝑗 𝑛+1 2⁄ 𝑉0,𝑗 𝑛+1 −𝑉1,𝑗 𝑛+1 2 + 𝑉0,𝑗 𝑛 −𝑉1,𝑗 𝑛 2 + 𝑘 𝑠  𝑘 𝑠 = log 1 − đŸđ‘ 
  • 41.
    Penalty 41  đœ‰Ì‚ 0,𝑗 𝑛+1 2⁄ =ïżœ 𝜉∆𝑡, if 𝑉1,𝑗 𝑛+1 −𝑉0,𝑗 𝑛+1 2 + 𝑉1,𝑗 𝑛 −𝑉0,𝑗 𝑛 2 − 𝑘 𝑏 > 0 0, otherwise  đœ‰Ì‚ 1,𝑗 𝑛+1 2⁄ = ïżœ 𝜉∆𝑡, if 𝑉0,𝑗 𝑛+1 −𝑉1,𝑗 𝑛+1 2 + 𝑉0,𝑗 𝑛 −𝑉1,𝑗 𝑛 2 + 𝑘 𝑠 > 0 0, otherwise
  • 42.
    The Discretized PDEs 42 ïœđ‘Ž1,𝑗 𝑉0,𝑗+1 𝑛+1 + 𝑎0,𝑗 𝑉0,𝑗 𝑛+1 + 𝑎−1,𝑗 𝑉0,𝑗−1 𝑛+1 = 𝑐0,𝑗 𝑛 + đœ‰Ì‚ 0,𝑗 𝑛+1 2⁄ 𝑉1,𝑗 𝑛+1 −𝑉0,𝑗 𝑛+1 2 + 𝑉1,𝑗 𝑛 −𝑉0,𝑗 𝑛 2 − 𝑘 𝑏  𝑎1,𝑗 𝑉1,𝑗+1 𝑛+1 + 𝑎0,𝑗 𝑉1,𝑗 𝑛+1 + 𝑎−1,𝑗 𝑉1,𝑗−1 𝑛+1 = 𝑐1,𝑗 𝑛 + đœ‰Ì‚ 1,𝑗 𝑛+1 2⁄ 𝑉0,𝑗 𝑛+1 −𝑉1,𝑗 𝑛+1 2 + 𝑉0,𝑗 𝑛 −𝑉1,𝑗 𝑛 2 + 𝑘 𝑠  𝑗 ∈ 1, ⋯ , 𝑀 − 1  𝑝 = 0, 𝑝 = 1 are excluded.
  • 43.
    The Coefficients 43  𝑎−1,𝑗= − 1 2 𝜎 𝑝 2 ∆𝑡 2∆𝑝2 + 1 2 𝜇 𝑝 ∆𝑡 2∆𝑝  𝑎0,𝑗 = 1 + 𝜎 𝑝 2 ∆𝑡 2∆𝑝2  𝑎1,𝑗 = − 1 2 𝜎 𝑝 2 ∆𝑡 2∆𝑝2 − 1 2 𝜇 𝑝 ∆𝑡 2∆𝑝  𝑐0,𝑗 𝑛 = −𝑎1,𝑗 𝑉0,𝑗+1 𝑛 + 2 − 𝑎0,𝑗 𝑉0,𝑗 𝑛 − 𝑎−1,𝑗 𝑉0,𝑗−1 𝑛 + ℎ 𝑗∆𝑝 ∆𝑡  𝑐1,𝑗 𝑛 = −𝑎1,𝑗 𝑉1,𝑗+1 𝑛 + 2 − 𝑎0,𝑗 𝑉1,𝑗 𝑛 − 𝑎−1,𝑗 𝑉1,𝑗−1 𝑛 + 𝑓 𝑗∆𝑝 ∆𝑡
  • 44.
    Boundary Conditions 44  𝑗= 0, 𝑝 = 0  𝑎0,0=1  𝑎1,0 = 0  𝑐0,0 𝑛 = 𝑉0,1 𝑛 + ℎ 0 ∆𝑡  𝑐1,0 𝑛 = 𝑉1,1 𝑛 + 𝑓 0 ∆𝑡  𝑗 = 𝑀, 𝑝 = 1  𝑎0,𝑀=1  𝑎−1,𝑀 = 0  𝑐0,𝑀 𝑛 = 𝑉0,𝑀−1 𝑛 + ℎ 1 ∆𝑡  𝑐1,𝑀 𝑛 = 𝑉1,𝑀−1 𝑛 + 𝑓 1 ∆𝑡  𝑛 = 0, 𝑡 = 0, for all 𝑗 ∈ 0, ⋯ , 𝑀  𝑉0,𝑗 = 0  𝑉1,𝑗 = 𝑘 𝑠
  • 45.
    System in MatrixForm 45  ïżœ 𝐮 𝑛 𝑉0 𝑛+1 = 𝑐⃗0 𝑛 𝐮 𝑛 𝑉1 𝑛+1 = 𝑐⃗1 𝑛  𝐮 𝑛 = 𝑎0,0 𝑎−1,1 ⋼ 0 0 0 𝑎0,1 ⋱ 
 
 0 𝑎1,1 ⋱ 𝑎−1,𝑀−1 0 
 
 ⋱ 𝑎0,𝑀−1 0 0 0 ⋼ 𝑎1,𝑀−1 𝑎0,𝑀
  • 46.
    Solving the Systemof Equations 46  We already know the values of 𝑉0 0 and 𝑉1 0 .  Starting from 𝑛 = 0, using 𝐮 𝑛, we iteratively solve for 𝑉0 𝑛+1 and 𝑉1 𝑛+1 until 𝑛 = 𝑀 − 1.  There are totally M systems of equations to solve.  The equations are linear in the unknowns 𝑉0,𝑗 𝑛+1 and 𝑉1,𝑗 𝑛+1 if and only if đœ‰Ì‚ 0,𝑗 𝑛+1 2⁄ = 0.  When the equations are linear, we can use Thomas’ algorithm to solve for a tri-diagonal system of linear equations.  Otherwise, we use an iterative scheme.
  • 47.
    Iterative Scheme 47  1ststep, initialization, 𝑘 = 0  Assume đœ‰Ì‚ 𝑖,𝑗 𝑛+1 2⁄ 0 = 0. Solve for 𝑉𝑖 𝑛+1 0 .  kth step  Using 𝑉𝑖 𝑛+1 𝑘 − 1 , update đœ‰Ì‚ 𝑖,𝑗 𝑛+1 2⁄ 𝑘 .  When đœ‰Ì‚ 𝑖,𝑗 𝑛+1 2⁄ 𝑘 > 0, adjust the 𝐮 𝑛 𝑘 and 𝑐⃗𝑖 𝑛 𝑘 .  Repeat until convergence.
  • 48.
    Adjustments (A) 48  𝐮𝑛 𝑘 = 𝑎0,0 + 𝜉Δ𝑡 2 𝑎−1,1 ⋼ 0 0 0 𝑎0,1 + 𝜉Δ𝑡 2 ⋱ 
 
 0 𝑎1,1 ⋱ 𝑎−1,𝑀−1 0 
 
 ⋱ 𝑎0,𝑀−1 + 𝜉Δ𝑡 2 0 0 0 ⋼ 𝑎1,𝑀−1 𝑎0,𝑀 + 𝜉Δ𝑡 2
  • 49.
    Adjustments (c) 49  𝑐⃗0 𝑛 𝑘= 1 + 𝜉Δ𝑡 𝑉1,0 𝑛+1 𝑘−1 2 + 𝑉1,0 𝑛 −𝑉0,0 𝑛 2 − 𝑘 𝑏 𝑐0,1 𝑛 + 𝜉Δ𝑡 𝑉1,1 𝑛+1 𝑘−1 2 + 𝑉1,1 𝑛 −𝑉0,1 𝑛 2 − 𝑘 𝑏 ⋼ 𝑐0,𝑀−1 𝑛 + 𝜉Δ𝑡 𝑉1,𝑀−1 𝑛+1 𝑘−1 2 + 𝑉1,𝑀−1 𝑛 −𝑉0,𝑀−1 𝑛 2 − 𝑘 𝑏 1 + 𝜉Δ𝑡 𝑉1,𝑀 𝑛+1 𝑘−1 2 + 𝑉1,𝑀 𝑛 −𝑉0,𝑀 𝑛 2 − 𝑘 𝑏  𝑐⃗1 𝑛 𝑘 = 1 + 𝜉Δ𝑡 𝑉0,0 𝑛+1 𝑘−1 2 + 𝑉0,0 𝑛 −𝑉1,0 𝑛 2 + 𝑘 𝑠 𝑐1,1 𝑛 + 𝜉Δ𝑡 𝑉0,1 𝑛+1 𝑘−1 2 + 𝑉0,1 𝑛 −𝑉1,1 𝑛 2 + 𝑘 𝑠 ⋼ 𝑐1,𝑀−1 𝑛 + 𝜉Δ𝑡 𝑉0,𝑀−1 𝑛+1 𝑘−1 2 + 𝑉0,𝑀−1 𝑛 −𝑉1,𝑀−1 𝑛 2 + 𝑘 𝑠 1 + 𝜉Δ𝑡 𝑉0,𝑀 𝑛+1 𝑘−1 2 + 𝑉0,𝑀 𝑛 −𝑉1,𝑀 𝑛 2 + 𝑘 𝑠
  • 50.
  • 51.
  • 52.
    Model Estimation 52  Estimatethe transition probabilities in the HMM by EM.  Estimate 𝜇 and 𝜎.  The log of the prices are Gaussian.  đœŽïżœ2: sample variance  đœŽïżœ2 = 𝜎2 Δ𝑡  𝜎 = đœŽïżœ 1 Δ𝑡  đ‘šïżœ 𝑖: sample mean  đ‘šïżœ 𝑖 = 𝜇𝑖 − 𝜎2 2 Δ𝑡  𝜇𝑖 = 1 Δ𝑡 đ‘šïżœ 𝑖 + 𝜎2 2