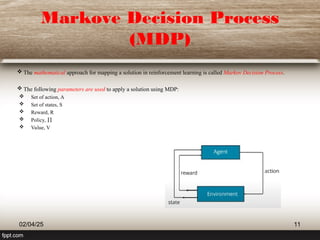
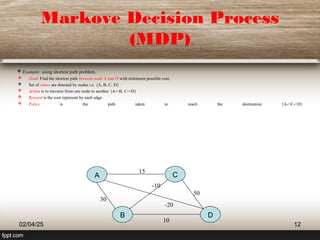
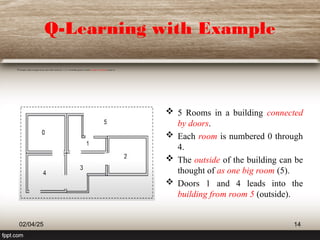
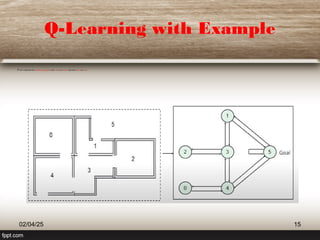
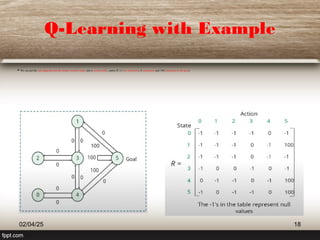
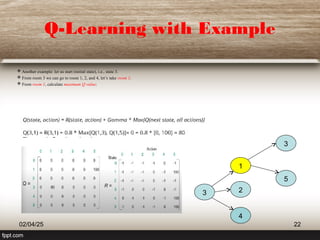
The document outlines the principles of reinforcement learning, a subset of machine learning where an agent learns behavior through interaction with an environment. Key components include the agent, environment, actions, states, and rewards, with a focus on maximizing rewards through exploration and exploitation. The document also explains q-learning, a value-based algorithm used for determining optimal action-selection policy, illustrated with examples such as navigating rooms with associated rewards.