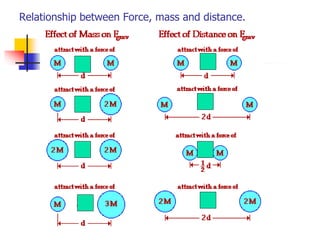
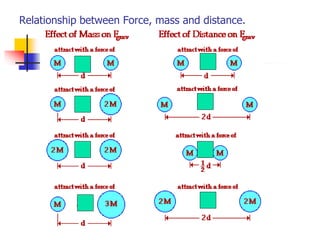
Newton's Universal Law of Gravitation describes the gravitational force between two masses. The force is directly proportional to the product of the masses and inversely proportional to the square of the distance between them. Kepler's Laws of Planetary Motion describe the motion of planets around the sun, including that their orbits are ellipses with the sun at one focus, they sweep out equal areas in equal times, and the squares of their orbital periods are proportional to the cubes of their distances from the sun. A satellite stays in orbit around a planet when its centripetal force due to its velocity balances the gravitational force exerted by the planet.

1. Newton's Universal Law of
Gravitation

2. Newton's Universal Law of Gravitation
 The gravitational force that exists between
two masses 𝑚1 and 𝑚2 is given by
𝑭 𝒈 = 𝑮
𝒎 𝟏 𝒎 𝟐
𝒓 𝟐
where 𝑟 - is the distance of separation
between their centers.
𝐺 = 6.67 𝑥 10−11 Nm2/kg2
- universal gravitation constant
𝑟
𝑚1 𝑚2𝐹𝑔 𝐹𝑔

3. Relationship between Force, mass and distance.

4. Relationship between Force, mass and distance.

5. 𝑚1
𝑚2
𝑚3
𝑟1
𝑟2
𝐹31
𝐹21
NET GRAVITATIONAL FORCE
For three or more objects, finding the net
gravitational force is by component!
REVIEW YOUR COMPONENT METHOD!!!
𝐹31
𝐹21 𝐹1
Cartesian Plane:

6. Gravitational Field Strength & Gravitational Acceleration
A gravitational field (popularly known as acceleration due
to gravity) is created by an object causing masses inside it
to experience the gravitational force.
e𝑥𝑎𝑚𝑝𝑙𝑒: 𝑔 𝐸 = 9.8 m/𝑠2

7. Gravity Near The Earth’s Surface
At the Earth’s surface:
𝐹𝑔 = 𝑤
𝐺
𝑚𝑚 𝐸
𝑟𝐸
2
= 𝑚𝑔 𝐸
𝑔 𝐸 = 𝐺
𝑚 𝐸
𝑟𝐸
2
= 9.8 m/s2
In general: 𝑔 𝑝 = 𝐺
𝑚 𝑝
𝑟𝑝
2
Gravitational field at the object’s
surface
where 𝑚 𝑝 = mass of the object having the field
𝑟𝑝 = radius of that object
𝑚 𝐸 = mass of the earth
𝑟𝐸 = radius of the earth

8. 𝒓
The effective g, g’
As you go far from the Earth’s surface,
the gravitational field decreases.
So, the effective g (g’):
where 𝑦 = distance above object′
s surface
𝑟 = 𝑟𝑝 + 𝑦
(𝑟 > 𝑟𝑝)
𝑔′ = 𝐺
𝑚 𝑝
𝑟2
Since 𝑔 𝑝 = 𝐺
𝑚 𝑝
𝑟 𝑝
2
𝑔′ = 𝑔 𝑝
𝑟𝑝
𝑟
2

9. Sample Problems:
1. Two objects attract each other with a
gravitational force of magnitude
1.00 𝑥 10−8 N when separated by 20.0 cm.
If the total mass of the objects is 5.00 kg,
what is the mass of each?
2. Calculate the effective value of g, at 3200 m
and 3200 km above the earth’s surface.
3. Calculate the velocity of a satellite moving
in a stable circular orbit about the Earth at a
height of 3600 km.

10. Satellite Motion and Weightlessness
without gravity
With gravity
Artificial satellite is put into
orbit by accelerating it to a
sufficiently tangential speed
with the use of the rocket.
If the speed is too high, the
satellite will escape.
If the speed is too low, it
will fall back to earth.
Fg

11. 𝐹𝑔 = 𝑚
𝑣2
𝑟 𝐺
𝑚𝑀
𝑟2
= 𝑚
𝑣2
𝑟
𝑣 = 𝐺
𝑀
𝑟
Speed of satellite at orbit radius r
where
𝑀 = mass of the object/planet that the satellite 𝑚 is orbiting

12. Satellite Motion and Weightlessness
The “weightlessness” experienced by a
person in a satellite orbit close to
Earth is the same apparent
weightlessness experienced in a freely
falling elevator.

14. Kepler’s Laws of Planetary Motion
Kepler’s First Law:
The path of each planet about the Sun is
an ellipse with the Sun at one focus
An Ellipse is a closed curve such that the sum of
the distances from any point P on the curve to
two fixed points (called the foci, F1 and F2)
remains constant.

16. Kepler’s Laws of Planetary Motion
Kepler’s Second Law:
Each planet moves so that an imaginary
line drawn from the Sun to the planet
sweeps out equal areas in equal periods
of time.

17. Sun
4
3

18. Kepler’s Laws of Planetary Motion
Kepler’s Third Law:
The ratio of the squares of the periods of
any two planets revolving around the
Sun is equal to the ratio of the cubes of
their mean distances from the Sun.

19. Sample Problems
1. Four 7.5-kg spheres are located at the corners of
a square of side 0.60 m. Calculate the net
gravitational force on one sphere due to the
other three.
2. Calculate the effective value of g, at 3200 m and
3200 km above the earth’s surface.
3. Calculate the velocity of a satellite moving in a
stable circular orbit about the Earth at a height of
3600 km.
4. Neptune is an average distance of 4.5 x 109 km
from the Sun. Estimate the length of the
Neptunian year given that the Earth is 1.50 x 108
km from the Sun on the average.

20. TERMINAL VELOCITY

21. Fg =mg
1. Object about
to start
falling. V=0
W=mg
2. Object is
falling. V>0
Friction
a 9.8 m/s2
Friction=Fg
a= m/s2
TERMINAL VELOCITY
3. The object now
moves with
TERMINAL
VELOCITY.
An object is dropped from REST.
V = max

22. Fg =mg
1. Object about
to start
falling. V=0
=mg
2. Object is
falling. V>0
Friction
a=10m/s2 The object
accelerates towards
the earth.
a<10 m/s2
Acceleration decreased!
Friction=
a= 0 m/s2
TERMINAL VELOCITY
3. The object now
moves with
TERMINAL
VELOCITY.
An object is dropped from REST.
V = maxFres < Fg