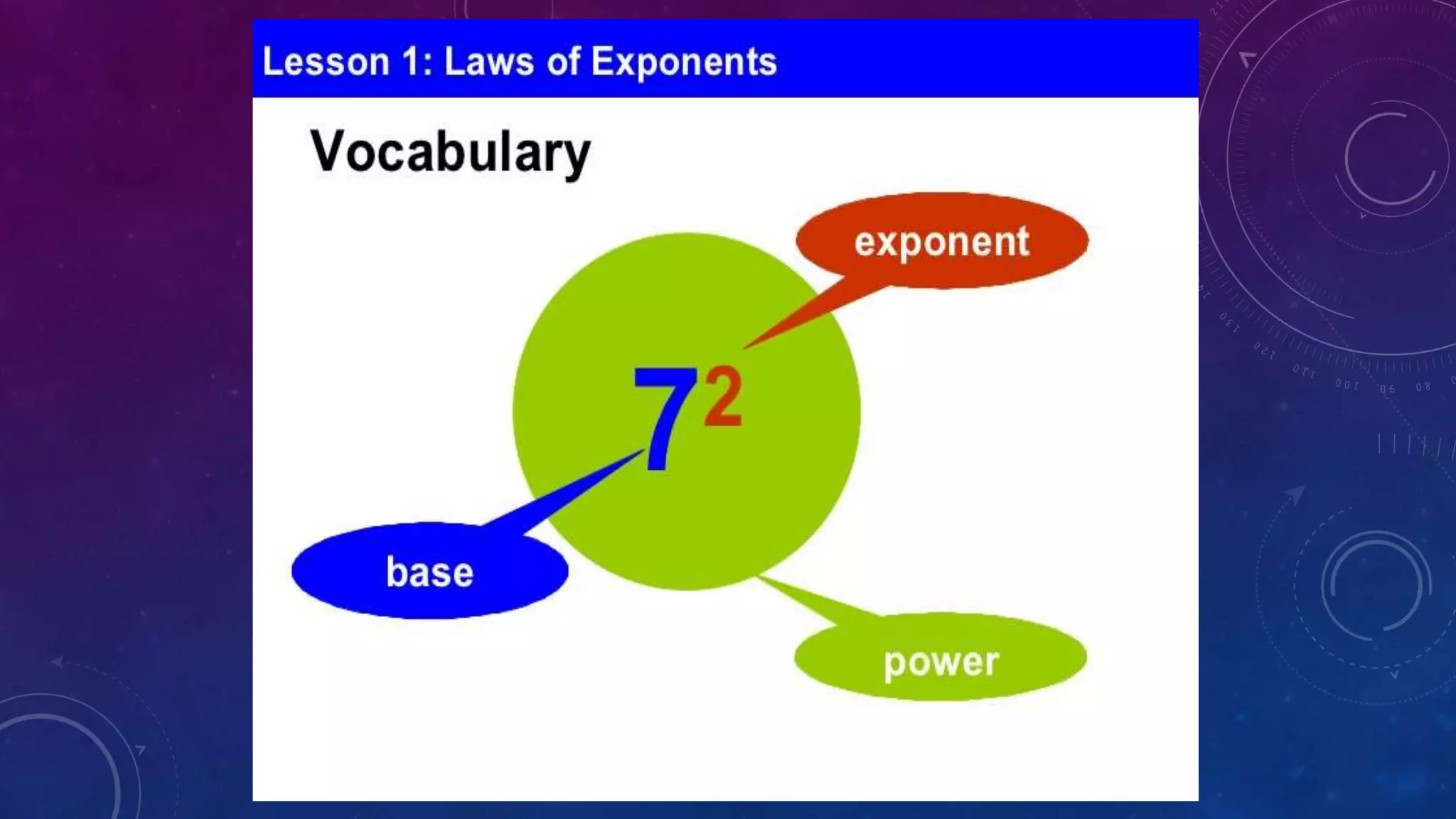
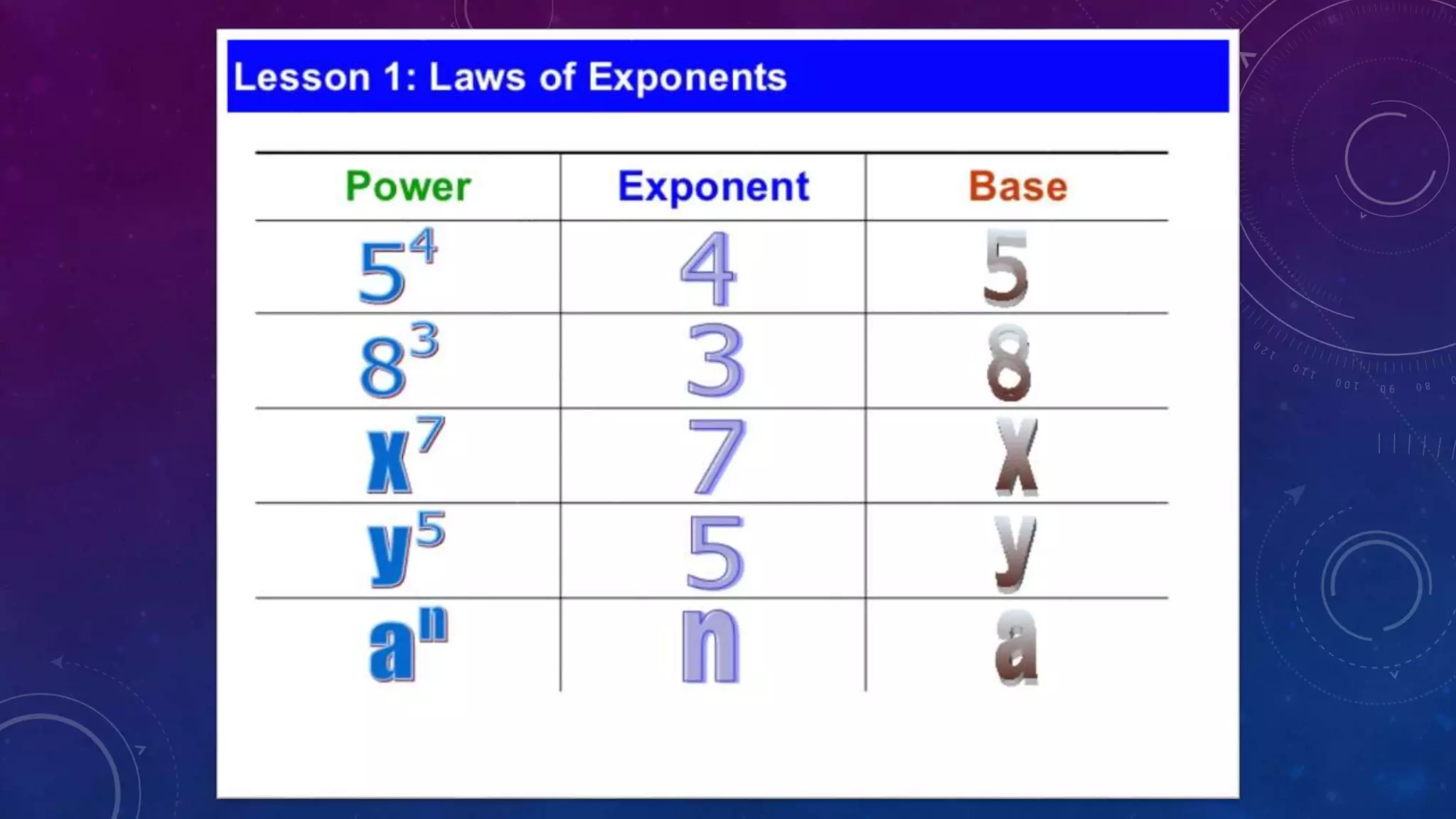
The document outlines the laws governing exponents and powers, including the product law, quotient law, and power law, with examples for each. It also explains the zero power rule and negative power rule, providing specific instances to illustrate the concepts. Overall, it serves as a comprehensive guide for understanding the fundamental operations involving exponents.

1. MATHS PROJECT
EXPONENTS AND
POWERS
MADE BY :A.SAMUEL PRABHU
DASS

4. LAW I:PRODUCT LAW
Examples:
1)x4 · x5 = x4+5 = x9
2)55 · 58 = 55+8 = 513
3)a7 · a · a12 = a7+1+12 = a20
4) (3x6)(2x4) = (3·2)x6+4= 6x10
am · an = am+n (when
multiplying like bases, add the
powers)

5. LAW II: QUOTIENT LAW
AM= AM - N (WHEN DIVIDING WITH LIKE BASES, SUBTRACT THE POWER)
AN (NOTE: IT IS ALWAYS THE NUMERATOR'S POWER MINUS THE
DENOMINATOR'S POWER)
Example:
1) x6 ÷ x4 = x2

6. LAW III:POWER LAW
(ambm)n = amnbmn
(when taking a monomial to a power, multiply the
powers including the coefficient)
EXAMPLES
1) (a4b3)2 = a8b6
2) (3m2n5)4 = 34m8n20 = 81m8n20
3) (-2xy7z2)5 = (-2)5x5y35z10 = -32x5y35z10

7. POWERS WITH DIFFERENT BASE

8. ZERO POWER RULE
a0 = 1 (any term to the zero power is one)
Examples:
1) (m5 n7)0 = 1
2) (4m8n2)(-2mn4)0 = (4m8n2)(1) = 4m8n2

9. NEGATIVE POWER RULE
a-n = 1 and 1 =an (take the reciprocal of the variable to the
negative power) NOTE: Apply the negative power rule to only
negative POWERS