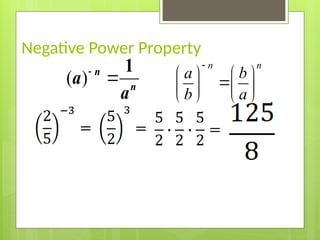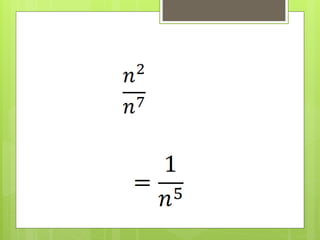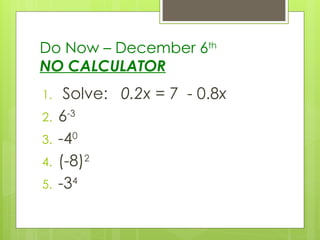Recommended
PPT
PPTX
Exponent Rules ppt.pptxExponent Rules ppt.pptx
PPT
Exponents and powers by arjun rastogi
PPTX
Introduction to exponents power point presentation
PPT
Exponents Intro with Practice.ppt
PPT
Law_of_Exponents_Grade7 Final Presentation
PPT
basicsaboutexponents-140308-phpapp01.ppt
PPT
basicsaboutexponents-140308083731-phpapp01.ppt
PPTX
PPT
Laws of exponents complete
PDF
What are Exponents and Powers? Definitions, Rules, and Examples
PPTX
Education_Exponents- and - its-laws.pptx
PDF
ppt L7.1 &7.2exponents(1).pdf PowerPoint
PPTX
PPTX
Division of numbers in exponential form
PPTX
Students are able to use exponent rules to simplify expressions.pptx
PPT
Laws of Exponents revised.pptttttttttttttt
PPT
Laws of Exponents - Applying Properties of Exponents
PPT
Repeated multiplication 123456789101.ppt
PPT
The Laws of Exponents revised edition.ppt
PPT
Laws of Exponents revised powerpoint pre
PPT
PPT
PPTX
Exponents and its laws.pptx
PPT
laws_of_exponents_student_use.ppt
PPT
laws_of_exponents_student_use.ppt
PPT
laws_of_exponents_student_use.ppt
PPT
laws_of_exponents_student_use.ppt
PPTX
"Aristotle : Father Of Western Philosophy"
PDF
Sharad Bisen_Soil Sterilization_Objectives_ICAR Course, Sixth Dean Committee.pdf
More Related Content
PPT
PPTX
Exponent Rules ppt.pptxExponent Rules ppt.pptx
PPT
Exponents and powers by arjun rastogi
PPTX
Introduction to exponents power point presentation
PPT
Exponents Intro with Practice.ppt
PPT
Law_of_Exponents_Grade7 Final Presentation
PPT
basicsaboutexponents-140308-phpapp01.ppt
PPT
basicsaboutexponents-140308083731-phpapp01.ppt
Similar to Exponent Rules ppt.pptxKKExponent Rules ppt.pptxKKExponent Rules ppt.pptxKK
PPTX
PPT
Laws of exponents complete
PDF
What are Exponents and Powers? Definitions, Rules, and Examples
PPTX
Education_Exponents- and - its-laws.pptx
PDF
ppt L7.1 &7.2exponents(1).pdf PowerPoint
PPTX
PPTX
Division of numbers in exponential form
PPTX
Students are able to use exponent rules to simplify expressions.pptx
PPT
Laws of Exponents revised.pptttttttttttttt
PPT
Laws of Exponents - Applying Properties of Exponents
PPT
Repeated multiplication 123456789101.ppt
PPT
The Laws of Exponents revised edition.ppt
PPT
Laws of Exponents revised powerpoint pre
PPT
PPT
PPTX
Exponents and its laws.pptx
PPT
laws_of_exponents_student_use.ppt
PPT
laws_of_exponents_student_use.ppt
PPT
laws_of_exponents_student_use.ppt
PPT
laws_of_exponents_student_use.ppt
Recently uploaded
PPTX
"Aristotle : Father Of Western Philosophy"
PDF
Sharad Bisen_Soil Sterilization_Objectives_ICAR Course, Sixth Dean Committee.pdf
PPTX
'Colonial Mentality and Social Identity in Karma by Khushwant Singh'
PPTX
How to Restrict Price Modification to Managers in Odoo 18 POS
PPTX
Reimagining Academic Library Services through Artificial Intelligence: A Case...
PDF
Q4_LE_English 5_Lesson 1_Week 1.pdf learning instruction
PPTX
Drug Distribution in Pharmacology: Mechanisms, Barriers, Factors & Volume of ...
PDF
Unit Plan and Unit Test-pdf-Dr. Rajashekhar Shirvalkar, Principal, SMRS B.Ed ...
PDF
Beak Modifications by Dr. Ramzan Virani pptx.pdf
PPTX
" Jaya : Silence as Resistance " - That long silence
PDF
APPSC APPSC AEE-AE GENERAL STUDIES QUESTION PAPER.pdf
PDF
CAM, DHT11, GAS, ESP32, FLAME, IR, TEMP, LCD, PIR, SOIL, SOUND, RELAY, TURBID...
PPTX
Biological source, chemical constituents, and therapeutic efficacy of the fol...
PPTX
COMMUNICATION ITS PROCESS ELEMENTS & BARRIER .pptx
PPTX
Metabolism ( BIOCHEMISTRY & CLINICAL PATHOLOGY )
PPTX
Central Line Associated Bloodstream Infection
PDF
Radio Ceylon Finals (An Indian Subcontinent Quiz).pdf
PDF
Lamarckism: Theory of Evolution, Principles, Examples, Objections and Neo-Lam...
PDF
Bishan_Singh_Presentation - Toba tek Singh
PDF
Fast Followers Project, Embedding Net Zero into Wakefield Metropolitan Distri...
Exponent Rules ppt.pptxKKExponent Rules ppt.pptxKKExponent Rules ppt.pptxKK 1. 2. 3. 4. 5. 6. 7. 8. 9. Any number raised to the first
power is …
31
=
871
=
5289211
=
Rule:
Any number raised to the first power
is
itself.
(a1
= a)
10. 11. 12. 13. 14. 15. Product Rule
Saying goes: BASE, BASE, ADD
If the BASES are same, ADD the powers
What are the base(s) and the power(s)?
4 5
2 2
m n m n
a a a
16. Product of a Power
m n m n
a a a
4 5 4 5
2 2 2
9
2
512
4 5
2 2
17. Product of a Power
m n m n
a a a
4 5 4 5
2 2 2
9
2
512
4 5
2 2
18. 19. Quotient Power Property
Saying goes: When dividing an expression with a
power, SUBTRACT the powers. They must have the
same base in order to subtract.
What are the base(s) and the power(s)?
8
3
x
x
m
m n
n
a
a
a
20. 21. 22. 23. Power of a Power
Saying goes: POWER, POWER, MULTIPLY
If the POWERS are near each other, MULTIPLY the powers
– usually deals with PARENTHESES
What are the base(s) and the power(s)?
3
2
3
( )
m n m n
a a
24. Power of a Power
( )
m n m n
a a
3
2 6
3 3
6
3
729
3
2
3
25. Power of a Power
( )
m n m n
a a
2
3
2
64
26. 27. Power of a Product
Saying goes: DISTRIBUTE THE POWER TO THE
BASES
What are the base(s) and the power(s)?
( )4
3x
( )
m m m
ab a b
28. Power of a Product
( )
m m m
ab a b
4 4 4
(3 ) (3) ( )
x x
4
81 x
x
4
81
4
(3 )
x
How many
bases does this
problem have?
29. Properties of Exponents
Negative Power Property:
Product of a Power:
Power of a Power:
Quotient Power Property:
m n m n
a a a
( )
m n m n
a a
( )
1
n
n
a
a
m
m n
n
a
a
a
30. Do Now – December 6th
NO CALCULATOR
1. Solve: 0.2x = 7 - 0.8x
2. 6-3
3. -40
4. (-8)2
5. -34