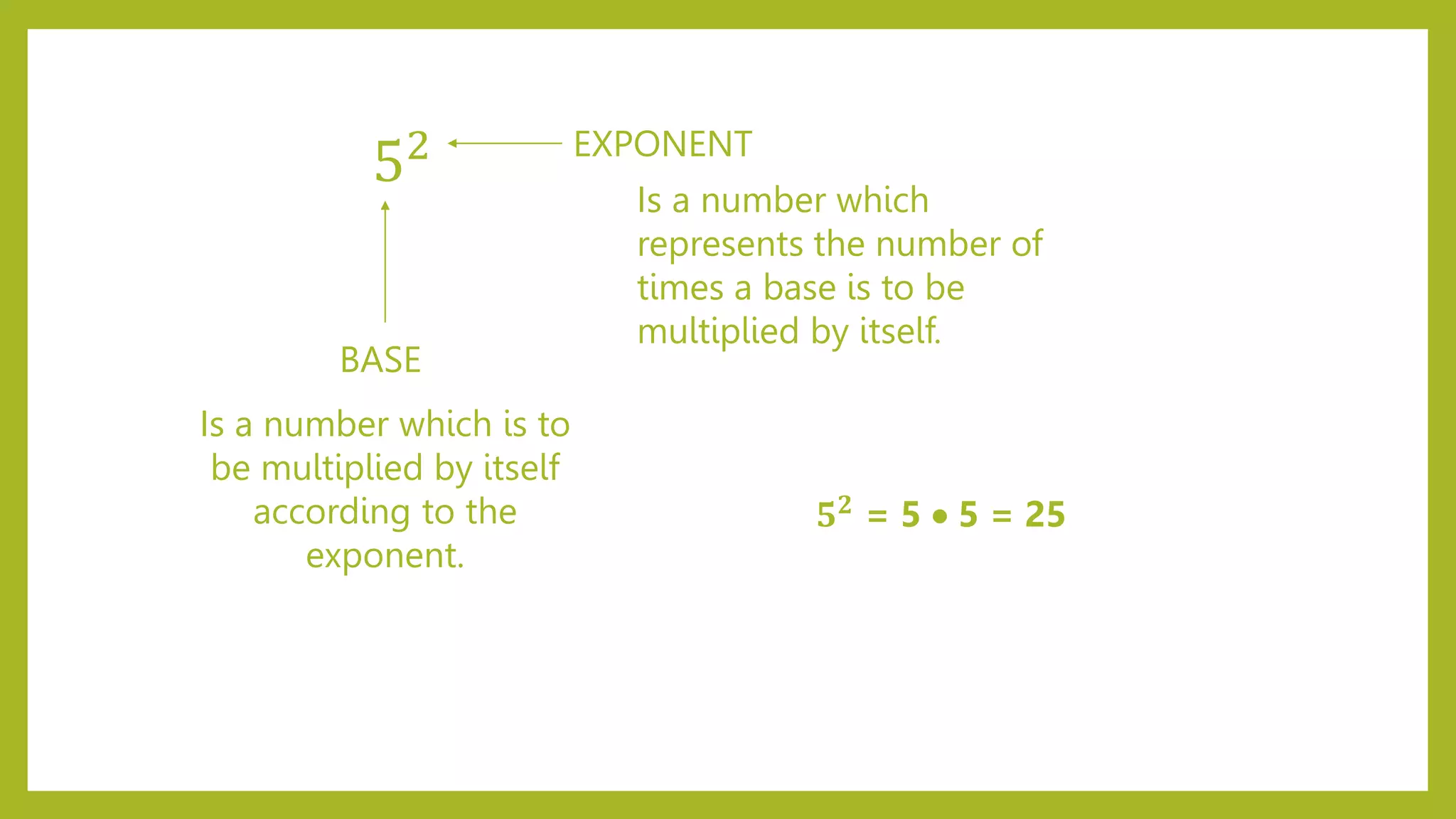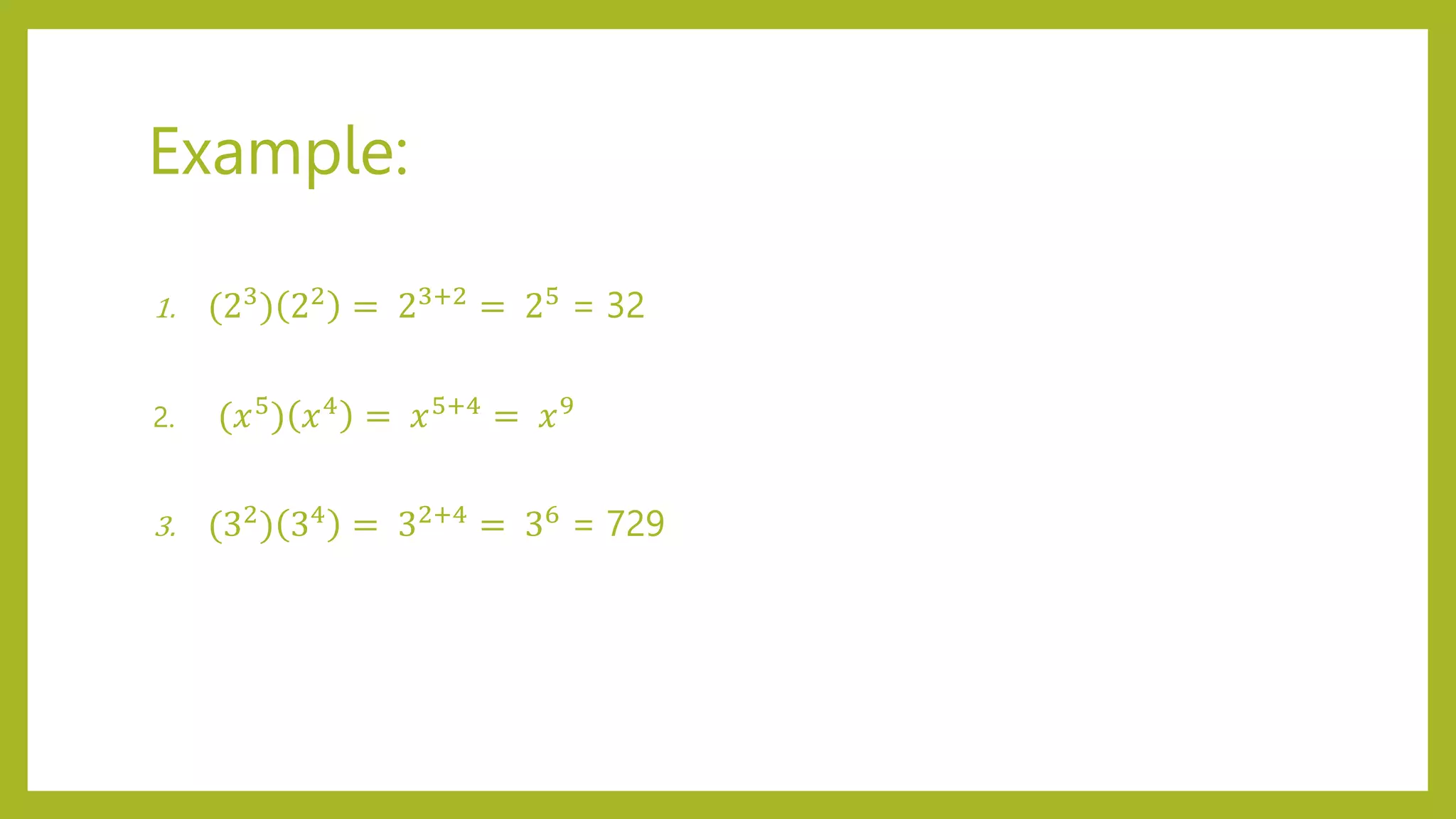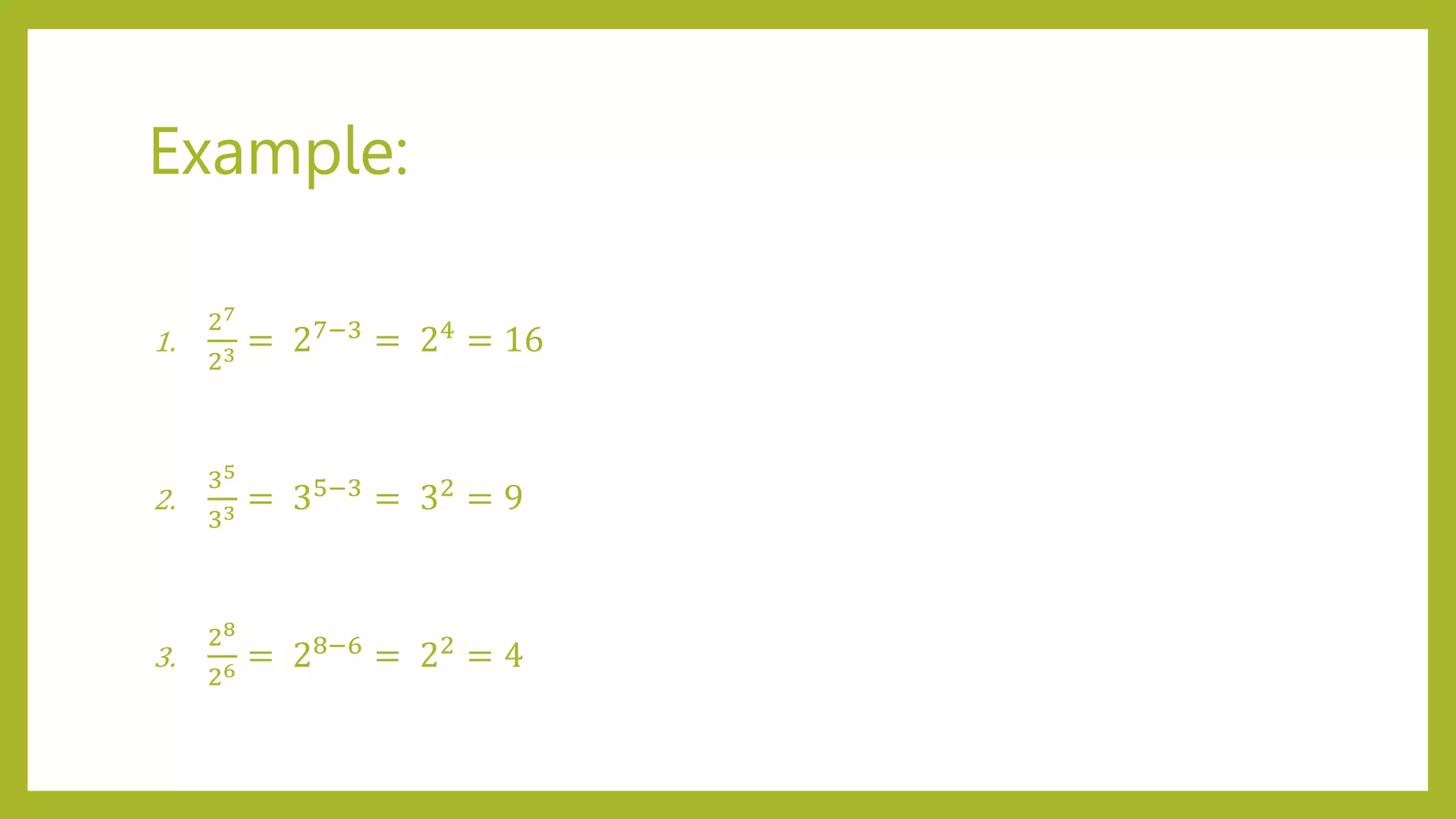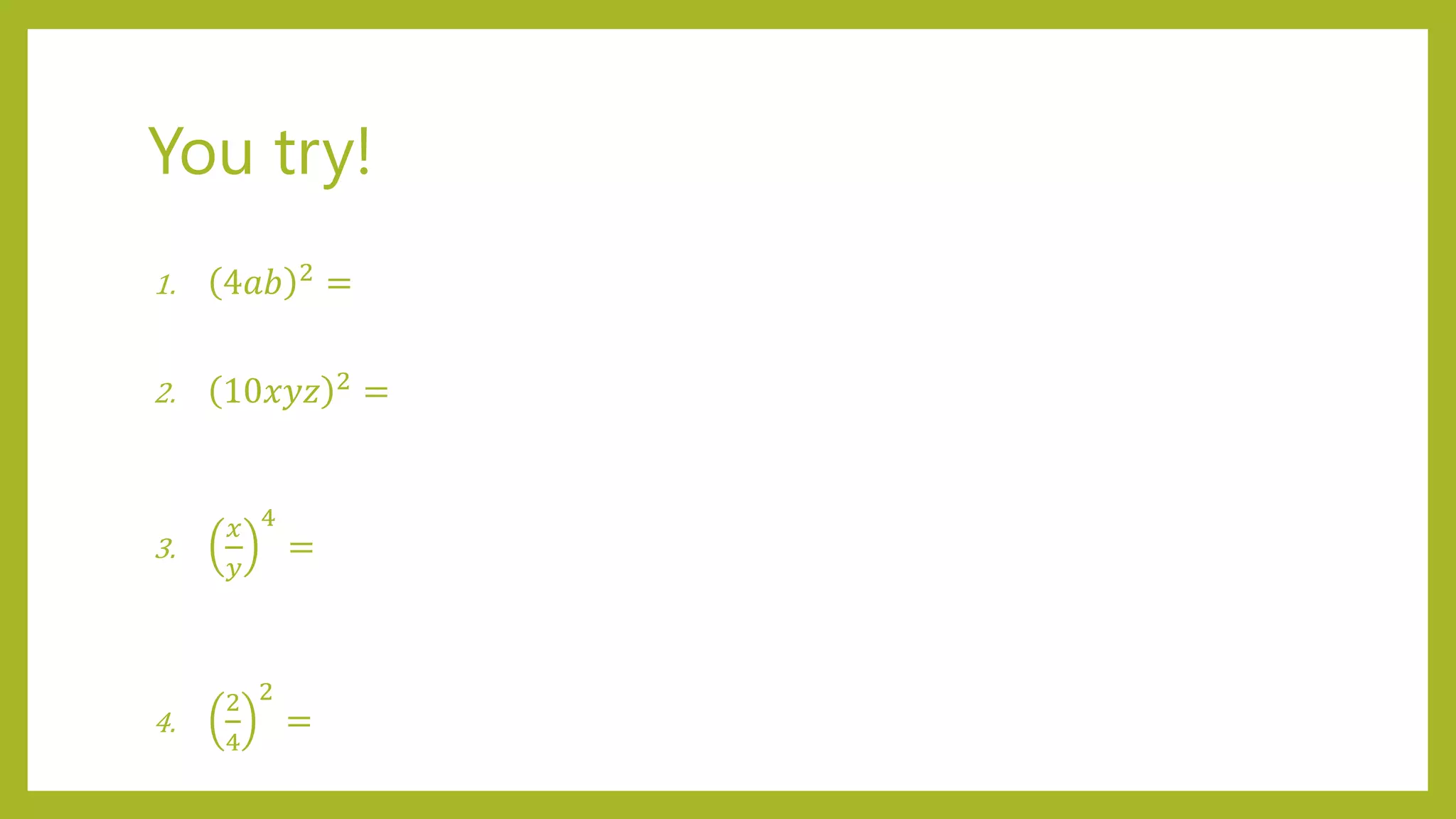This document discusses exponent laws and how to simplify expressions using exponents. It introduces six exponent laws: 1) Product Law, 2) Quotient Law, 3) Power of a Power Law, 4) Power with Different Bases Law, 5) Zero Exponent Law, and 6) Negative Exponent Law. Examples are provided to illustrate each law and how to use it to simplify exponential expressions. Readers are prompted to practice applying the laws to additional examples.

1. EXPONENTS AND ITS LAWS

2. EXPONENTIAL FORM
• Is an alternative method of expressing number.
For example:
𝑥2
, 22
, 23
, 52

3. 52 EXPONENT
BASE
Is a number which
represents the number of
times a base is to be
multiplied by itself.
Is a number which is to
be multiplied by itself
according to the
exponent.
𝟓𝟐
= 5  5 = 25

4. Law 1: Product Law
(𝑎𝑚) 𝑎𝑛 = 𝑎𝑚+𝑛
States that when multiplying two powers with the same base, just add
the exponents.

5. Example:
1. (23) 22 = 23+2 = 25 = 32
2. (𝑥5
) 𝑥4
= 𝑥5+4
= 𝑥9
3. (32) 34 = 32+4 = 36 = 729

6. You try!
1. (24) 25 =
2. (𝑥32
) 𝑥25
=
3. (𝑦59
) 𝑦51
=

7. Law 2: Quotient Law
𝑎𝑚
𝑎𝑛
= 𝑎𝑚−𝑛
States that when dividing two powers with the same base, just subtract
the exponents.

8. Example:
1.
27
23 = 27−3 = 24 = 16
2.
35
33 = 35−3
= 32
= 9
3.
28
26 = 28−6 = 22 = 4

9. You try!
1.
43
42 =
2.
𝑥20
𝑥13 =
3.
𝑦105
𝑦87 =

10. Law 3: Power of a power
𝑥𝑚 𝑛 = 𝑥𝑚𝑛
To simplify any power of power, simply multiply the exponents.

11. Example:
1. 23 2 = 2(3)(2) = 26 = 64
2. 𝑥4 3 = 𝑥(4)(3) = 𝑥12
3. 32 2 = 3(2)(2) = 34 = 81

12. You try!
1. 𝑎2 5 =
2. 22 3
=
3. 𝑥100 3 =

13. Law 4: Power with different bases
𝑏𝑐 𝑛 = 𝑏𝑛𝑐𝑛
𝑎
𝑏
𝑛
=
𝑎𝑛
𝑏𝑛
In dividing different bases, it can’t be simplified unless the exponents
are equal.

14. Example:
1. 2𝑥 2 = 22𝑥2 = 4𝑥2
2. 5𝑥𝑦 3
= 53
𝑥3
𝑦3
= 125𝑥3
𝑦3
3.
𝑥
3
2
=
𝑥2
32 =
𝑥2
9
4.
4
𝑎
2
=
42
𝑎2 =
16
𝑎2

15. You try!
1. 4𝑎𝑏 2 =
2. 10𝑥𝑦𝑧 2
=
3.
𝑥
𝑦
4
=
4.
2
4
2
=

16. Law 5: Zero Exponent
𝑎0 = 1
A nonzero base raised to zero the result is equal to one.
For example:
30 = 1
𝑥0 = 1
3𝑥
𝑦
0
= 1

17. You try!
1. 7, 645, 321 0
=
2. 30 + 𝑥0 + 3𝑦 0 =

18. Law 6: Negative Exponent
𝑎−𝑛 =
1
𝑎𝑛
A nonzero base raised to a negative exponent is equal to the reciprocal
of the base raised to the positive exponent.

19. Example:
1. 3−2 =
1
32 =
1
9
2. 2−8 =
1
28 =
1
256
3.
2
5
−6
=
5
2
6
=
56
26 =
15,625
64

20. You try!
1. 𝑥−2 =
2. 3−3
=
3. 5 − 3 −2
=

21. Law 1: Product Law (𝑎𝑚) 𝑎𝑛 = 𝑎𝑚+𝑛
Law 2: Quotient Law
𝑎𝑚
𝑎𝑛 = 𝑎𝑚−𝑛
Law 3: Power of a power 𝑥𝑚 𝑛 = 𝑥𝑚𝑛
Law 4: Power with different bases 𝑏𝑐 𝑛 = 𝑏𝑛𝑐𝑛 𝑎
𝑏
𝑛
=
𝑎𝑛
𝑏𝑛
Law 5: Zero Exponent

22. Let’s simplify!
1. (𝑥10) 𝑥12 =
2. (𝑦−3) 𝑦8 =
3. 𝑚15 3 =
4. 𝑑−3 2
=
5.
𝑏8
𝑏12 =
6. 𝑎−4 −4 =
7.
𝑧23
𝑧15 =
8.
𝑐3
𝑐−2 =
9.
𝑥7𝑦10
𝑥3𝑦5 =
10.
𝑎8𝑏2𝑐0
𝑎5𝑏5 =