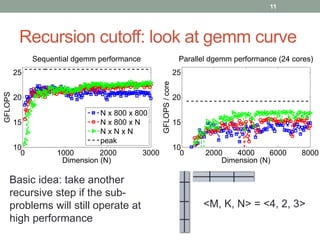
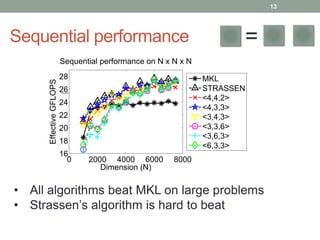
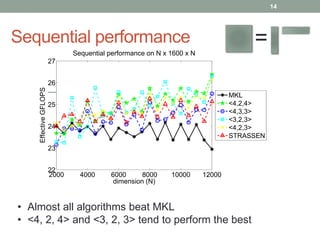
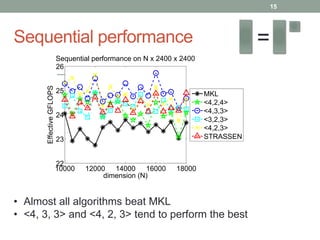
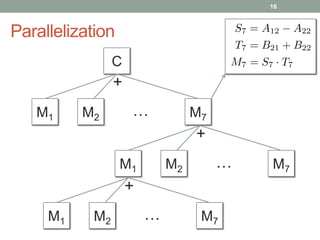
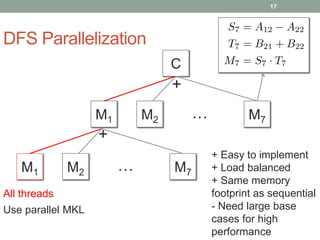
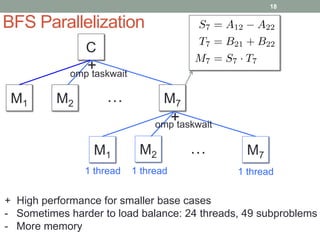
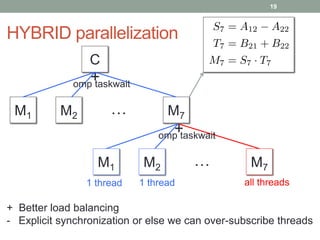
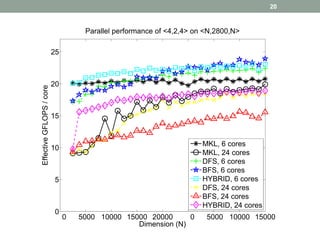
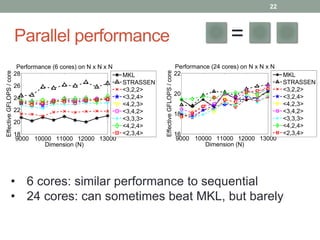
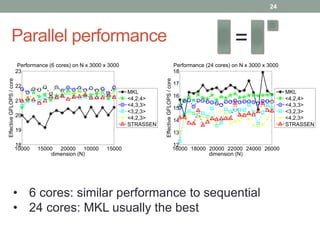
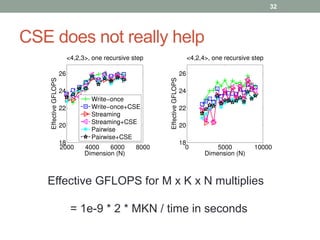
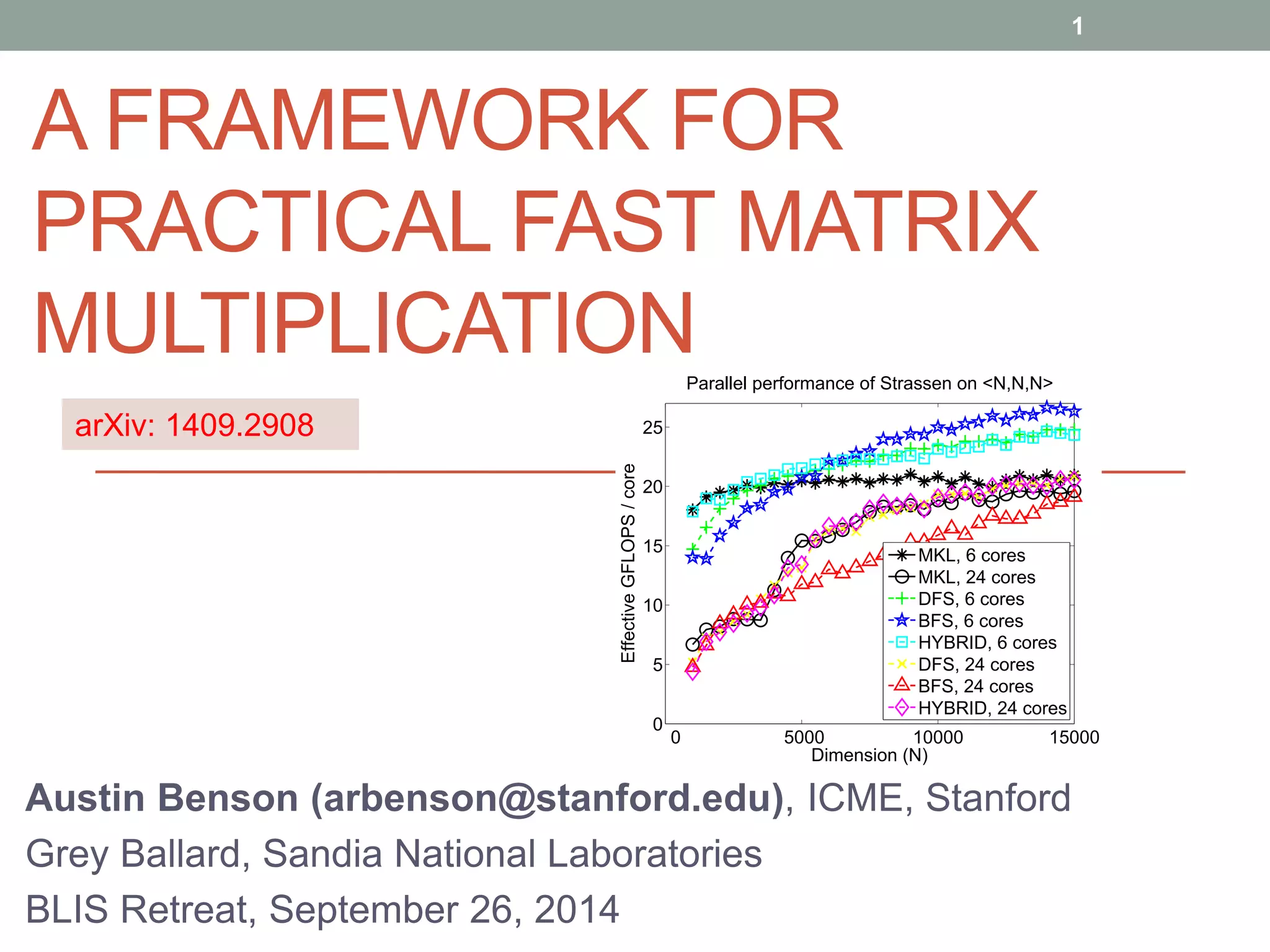
This document discusses frameworks for practical fast matrix multiplication algorithms. It summarizes several fast algorithms that improve on classical matrix multiplication and achieve higher performance than Intel MKL. Code generation is used to rapidly prototype various algorithms and evaluate their sequential and parallel performance on different problem sizes and shapes. The document finds that fast algorithms can outperform MKL for large problems, but parallel performance is limited by memory bandwidth issues for shared memory architectures. Future work includes improving numerical stability and applying fast matrix multiplication to other numerical linear algebra algorithms.
![Fast matrix multiplication:
bridging theory and practice
2
• There are a number of Strassen-like algorithms for matrix
multiplication that have only been “discovered” recently.
[Smirnov13], [Benson&Ballard14]
• We show that they can achieve higher performance with
respect to MKL (sequential and sometimes in parallel).
• We use code generation to do extensive prototyping. There
are several practical issues, and there is plenty of room for
improvement (lots of expertise at UT to help here!)
2 2.81 3
[Strassen79]
2.37
[Williams12]
xxxxx xxx x](https://image.slidesharecdn.com/blisfastmatmul-140930215339-phpapp01/85/A-framework-for-practical-fast-matrix-multiplication-BLIS-retreat-2-320.jpg)




![Discovering fast algorithms is a
numerical challenge
7
• Low-rank tensor decompositions lead to fast algorithms
• Tensors are small, but we need exact decompositions
NP-hard
• Use alternating least squares with regularization and
rounding tricks [Smirnov13], [Benson&Ballard14]
• We have around 10 fast algorithms for <M, K, N>
decompositions. Also have permutations, e.g., <K, M, N>.](https://image.slidesharecdn.com/blisfastmatmul-140930215339-phpapp01/85/A-framework-for-practical-fast-matrix-multiplication-BLIS-retreat-7-320.jpg)
![8
[Strassen69]
[Smirnov13]](https://image.slidesharecdn.com/blisfastmatmul-140930215339-phpapp01/85/A-framework-for-practical-fast-matrix-multiplication-BLIS-retreat-8-320.jpg)