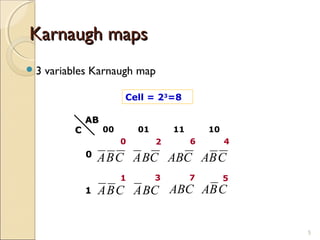
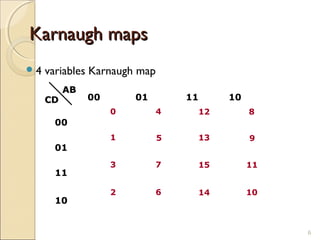
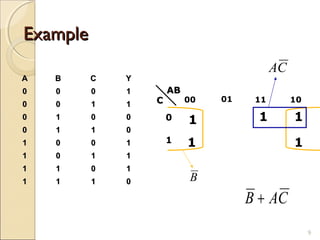
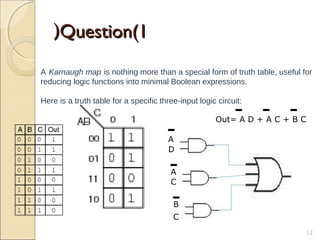
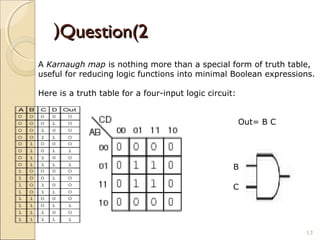
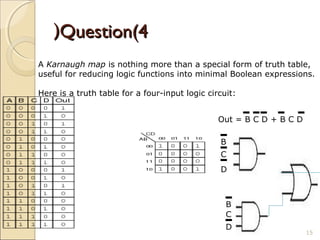
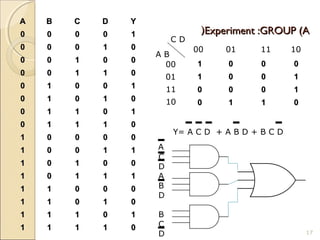
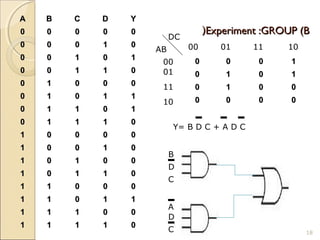
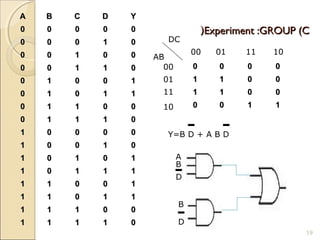
Karnaugh maps provide an alternative way to simplify logic circuits by visually grouping adjacent cells containing 1's and 0's in a map based on the truth table. The document provides examples of 2, 3, and 4 variable Karnaugh maps and explains how to construct the maps from truth tables and simplify logic functions into minimal Boolean expressions.

1. 1

2. Karnaugh MapsKarnaugh Maps (K maps)(K maps)
2

3. What are KarnaughWhat are Karnaugh11
maps?maps?
Karnaughmaps provide an alternative way of simplifying
logic circuits.
Instead of using Boolean algebra simplification
techniques, you can transfer logic values from a Boolean
statement or a truth table into a Karnaugh map.
The arrangement of 0's and 1's within the map helps
you to visualise the logic relationships between the
variables and leads directly to a simplified Boolean
statement.
1
Named for the American electrical engineer Maurice Karnaugh.
3

4. Karnaugh mapsKarnaugh maps
 Karnaugh maps, or K-maps, are often used to simplify logic problems with 2,
3 or 4 variables.
BA
For the case of 2 variables, we form a map consisting of 22
=4 cells
as shown in Figure
A
B
0 1
0
1
Cell = 2n
,where n is a number of variables
00 10
01 11
A
B
0 1
0
1
A
B
0 1
0
1
BA
BA AB
BA+ BA +
BA+ BA +
Maxterm Minterm
0 2
1 3
4

5. Karnaugh mapsKarnaugh maps
3 variables Karnaugh map
CBA
ABAB
CC 00 01 11 10
0
1
CBA CAB CBA
CBA BCA ABC CBA
0 2 6 4
531 7
Cell = 23
=8
5

6. Karnaugh mapsKarnaugh maps
4 variables Karnaugh map
ABAB
CDCD 00 01 11 10
00
01
11
10
5
3
1
7
62
0 4
9
15
13
11
1014
12 8
6

7. Karnaugh mapsKarnaugh maps
The Karnaugh map is completed by entering a '1‘(or
‘0’) in each of the appropriate cells.
Within the map, adjacent cells containing 1's (or 0’s)
are grouped together in twos, fours, or eights.
7

8. ExampleExample
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
2-variable Karnaugh maps are trivial but can be used to introduce
the methods you need to learn. The map for a 2-input OR gate
looks like this:
A
B
0 1
0
1
1
11
BB
AA
A+BA+B
8

9. ExampleExample
AA BB CC YY
00 00 00 11
00 00 11 11
00 11 00 00
00 11 11 00
11 00 00 11
11 00 11 11
11 11 00 11
11 11 11 00
CA
CAB +
B
ABAB
CC 00 01 11 10
0
1
1
1
1 1
1
9

10. Truth Table to K-Map MappingTruth Table to K-Map Mapping
10
Four Variable K-MapW X Y Z FWXYZ
0 0 0 0 1
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 1
0 1 0 1 0
0 1 1 0 0
0 1 1 1 1
1 0 0 0 1
1 0 0 1 0
1 0 1 0 0
1 0 1 1 0
1 1 0 0 1
1 1 0 1 0
1 1 1 0 0
1 1 1 1 1
V
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
XW
XW
XW
XW
ZY ZY ZY ZY
1 00 1
1 00 1
1 00 0
1 00 0
Only one
variable changes
for every row
change
Only one variable
changes for
every column
change
Fwxyz= Y Z + X Y Z

11. Individual WorkIndividual Work
11

12. Question(1Question(1((
A Karnaugh map is nothing more than a special form of truth table, useful for
reducing logic functions into minimal Boolean expressions.
Here is a truth table for a specific three-input logic circuit:
Out= A D + A C + B C
A
A
D
C
C
B
12

13. Question(2Question(2((
A Karnaugh map is nothing more than a special form of truth table,
useful for reducing logic functions into minimal Boolean expressions.
Here is a truth table for a four-input logic circuit:
Out= B C
B
C
13

14. Question(3Question(3((
A Karnaugh map is nothing more than a special form of truth table,
useful for reducing logic functions into minimal Boolean expressions.
Here is a truth table for a four-input logic circuit:
Out = A B
A
B
14

15. Question(4Question(4((
A Karnaugh map is nothing more than a special form of truth table,
useful for reducing logic functions into minimal Boolean expressions.
Here is a truth table for a four-input logic circuit:
Out = B C D + B C D
B
C
D
B
C
D
15

16. steps work experiment:
1.Solution truth table by
Karnaugh MapsKarnaugh Maps (K maps).(K maps).
2.2.Gate work by Karnaugh MapsGate work by Karnaugh Maps
(K maps).(K maps).
3.3.Applied to the gate on test Applied to the gate on test
board and make sure by truth board and make sure by truth
table.table.
16

17. Experiment :GROUP (AExperiment :GROUP (A((
AA BB CC DD YY
00 00 00 00 11
00 00 00 11 00
00 00 11 00 00
00 00 11 11 00
00 11 00 00 11
00 11 00 11 00
00 11 11 00 11
00 11 11 11 00
11 00 00 00 00
11 00 00 11 11
11 00 11 00 00
11 00 11 11 11
11 11 00 00 00
11 11 00 11 00
11 11 11 00 11
11 11 11 11 00
11 00 00 00
11 00 00 11
00 00 00 11
00 11 11 00
C D
A B
00
01
10
11
0100 1011
Y= A C D + A B D + B C D
A
C
D
A
B
D
B
C
D 17

18. Experiment :GROUP (BExperiment :GROUP (B((
AA BB CC DD YY
00 00 00 00 00
00 00 00 11 00
00 00 11 00 11
00 00 11 11 00
00 11 00 00 00
00 11 00 11 11
00 11 11 00 11
00 11 11 11 00
11 00 00 00 00
11 00 00 11 00
11 00 11 00 00
11 00 11 11 00
11 11 00 00 00
11 11 00 11 11
11 11 11 00 00
11 11 11 11 00
00 00 00 11
00 11 00 11
00 11 00 00
00 00 00 00
AB
DC
00
1000 1101
01
11
10
Y= B D C + A D C
B
D
C
A
D
C 18

19. Experiment :GROUP (CExperiment :GROUP (C((
AA BB CC DD YY
00 00 00 00 00
00 00 00 11 00
00 00 11 00 00
00 00 11 11 00
00 11 00 00 11
00 11 00 11 11
00 11 11 00 00
00 11 11 11 00
11 00 00 00 00
11 00 00 11 00
11 00 11 00 11
11 00 11 11 11
11 11 00 00 11
11 11 00 11 11
11 11 11 00 00
11 11 11 11 00
00 00 00 00
11 11 00 00
11 11 00 00
00 00 11 11
AB
DC
00
00
01
01 11
11
10
10
Y=B D + A B D
A
B
D
D
B
19

20. 22

21. 23