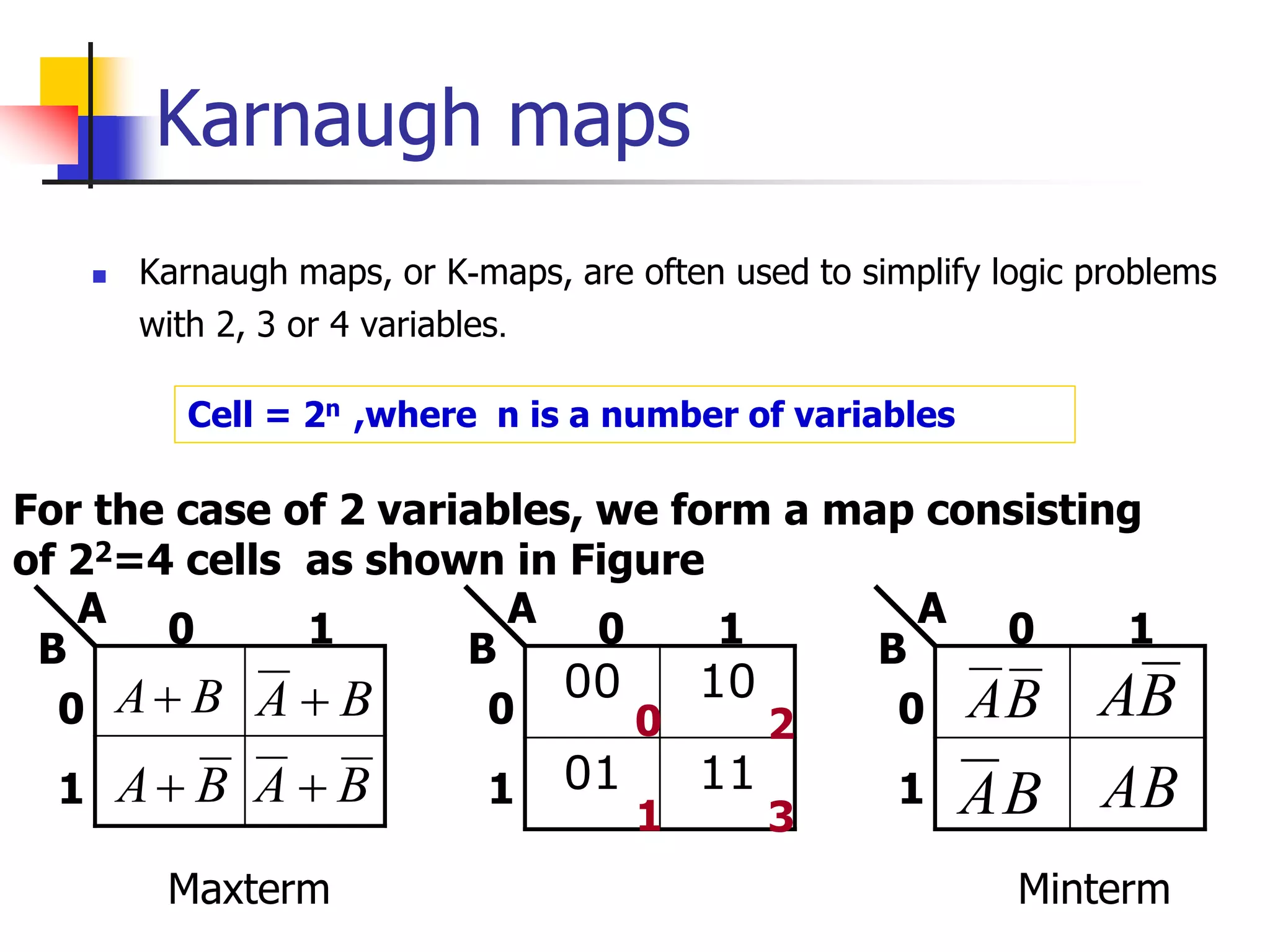
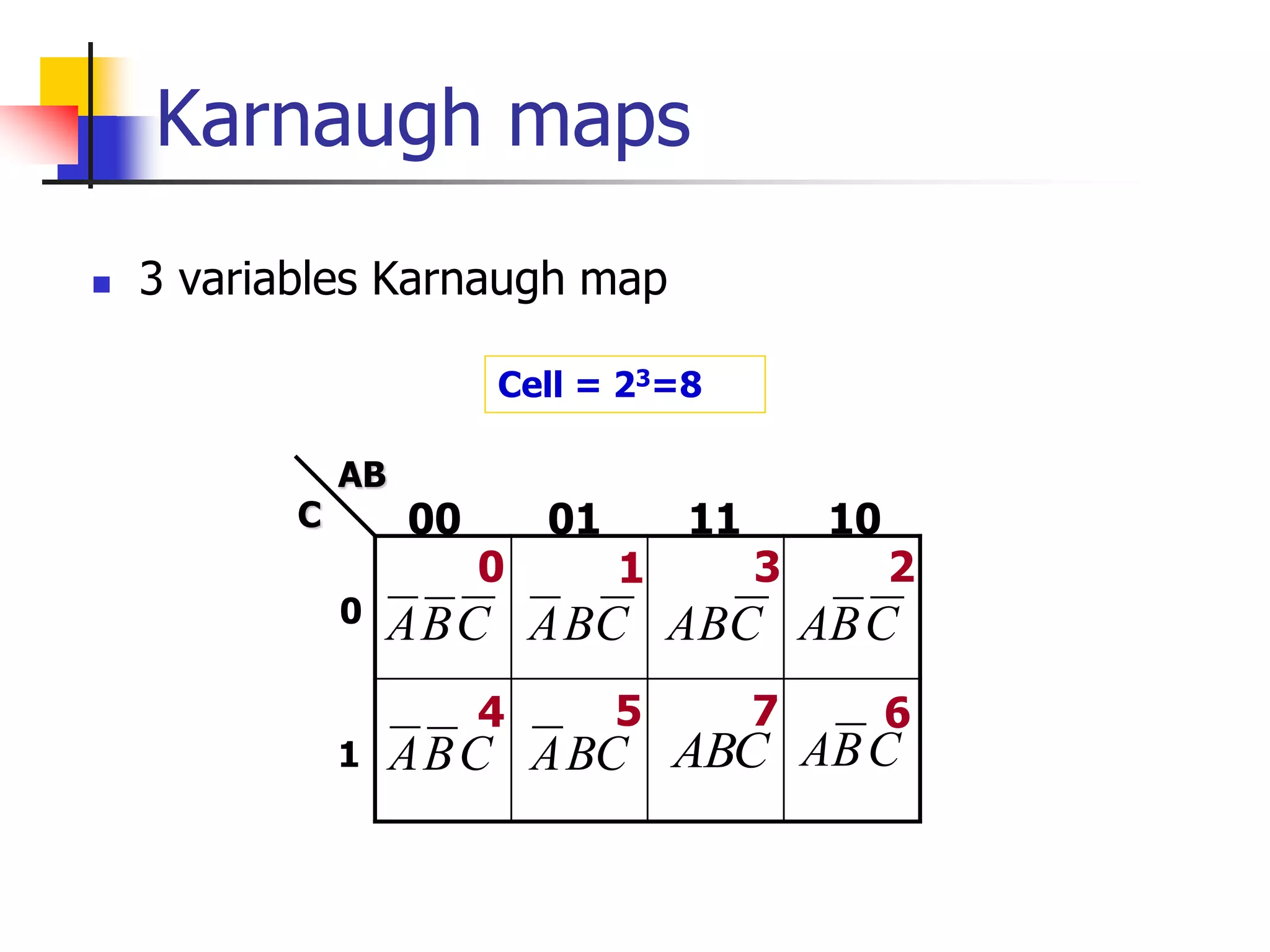
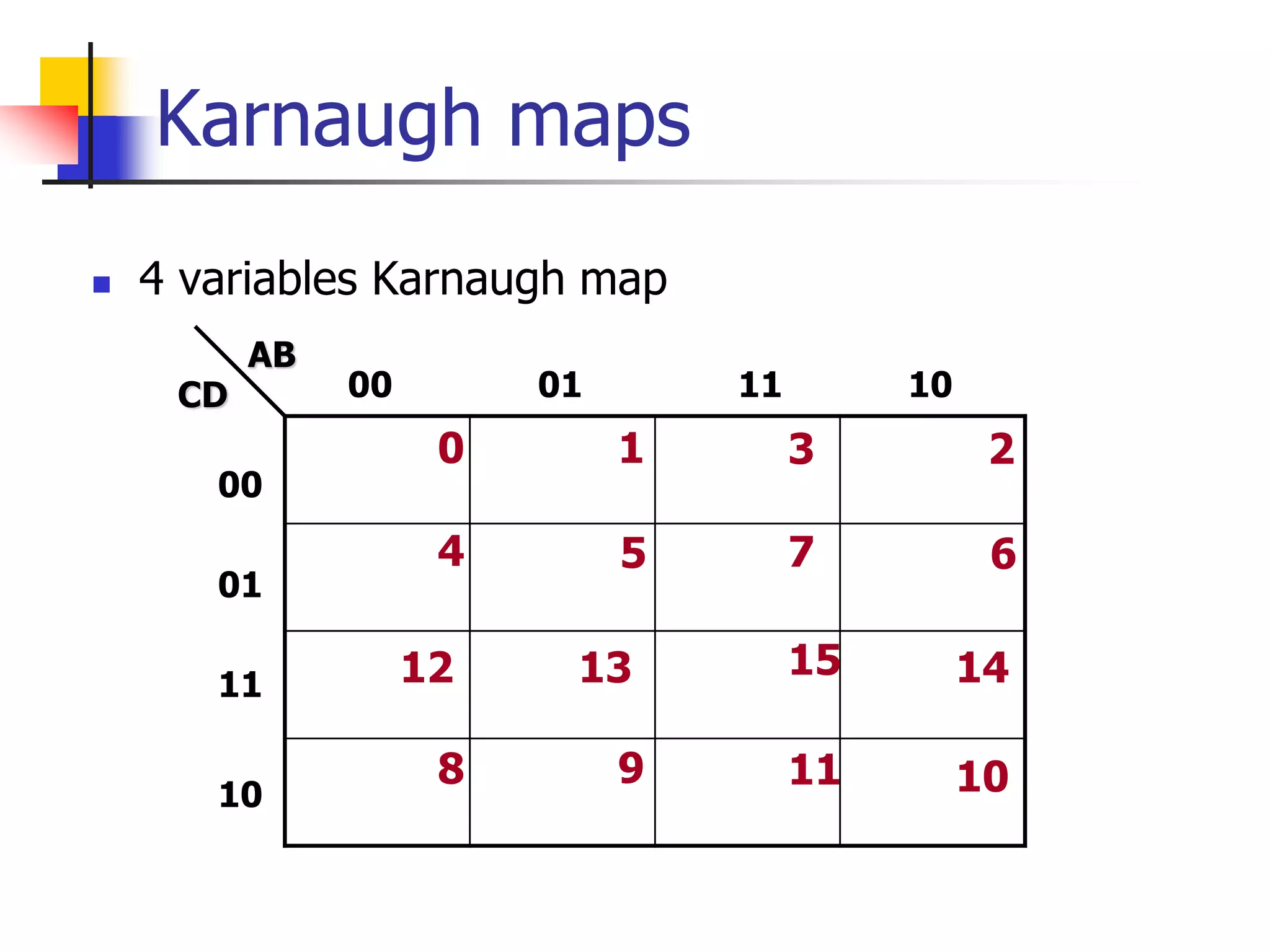
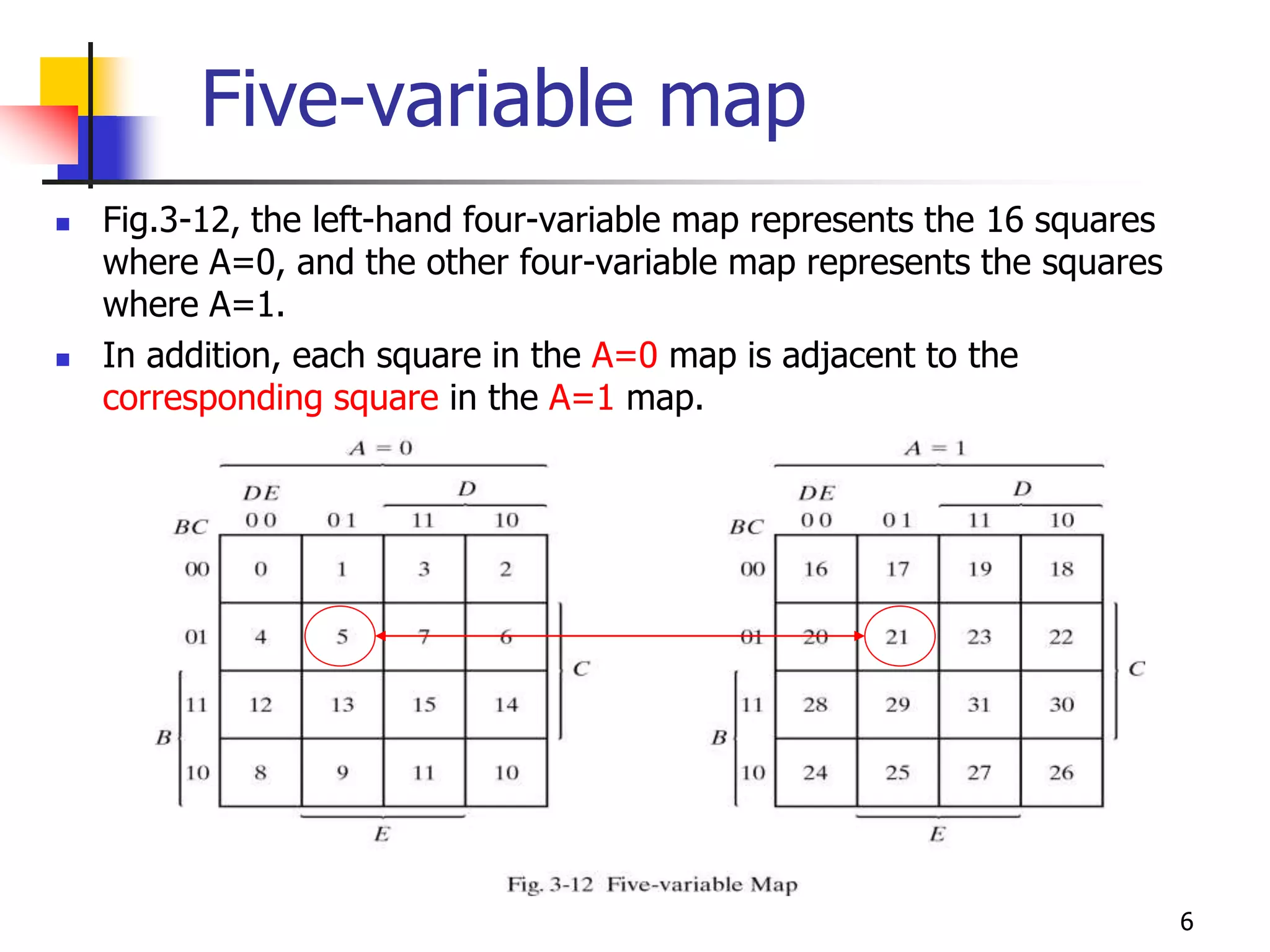
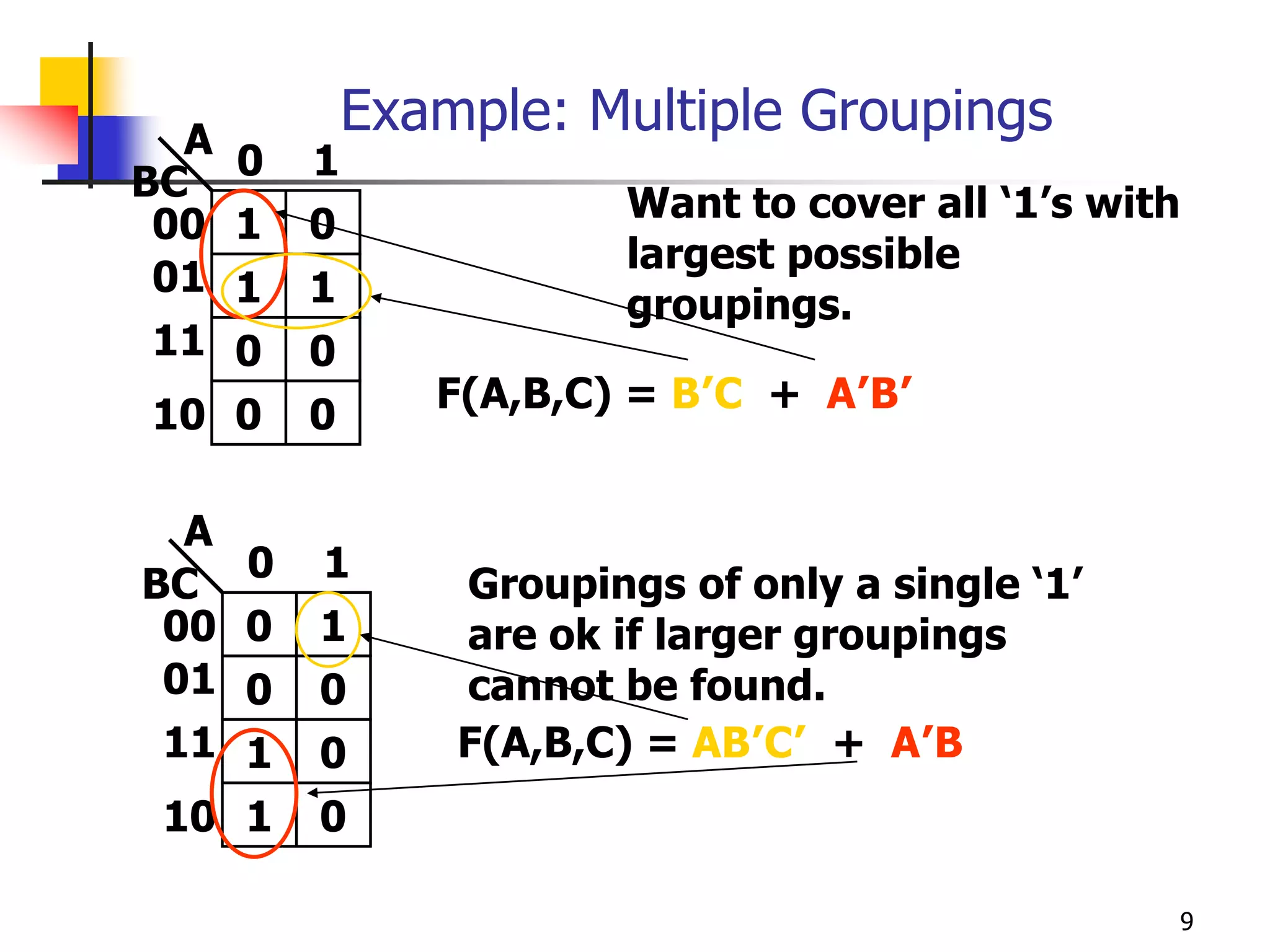
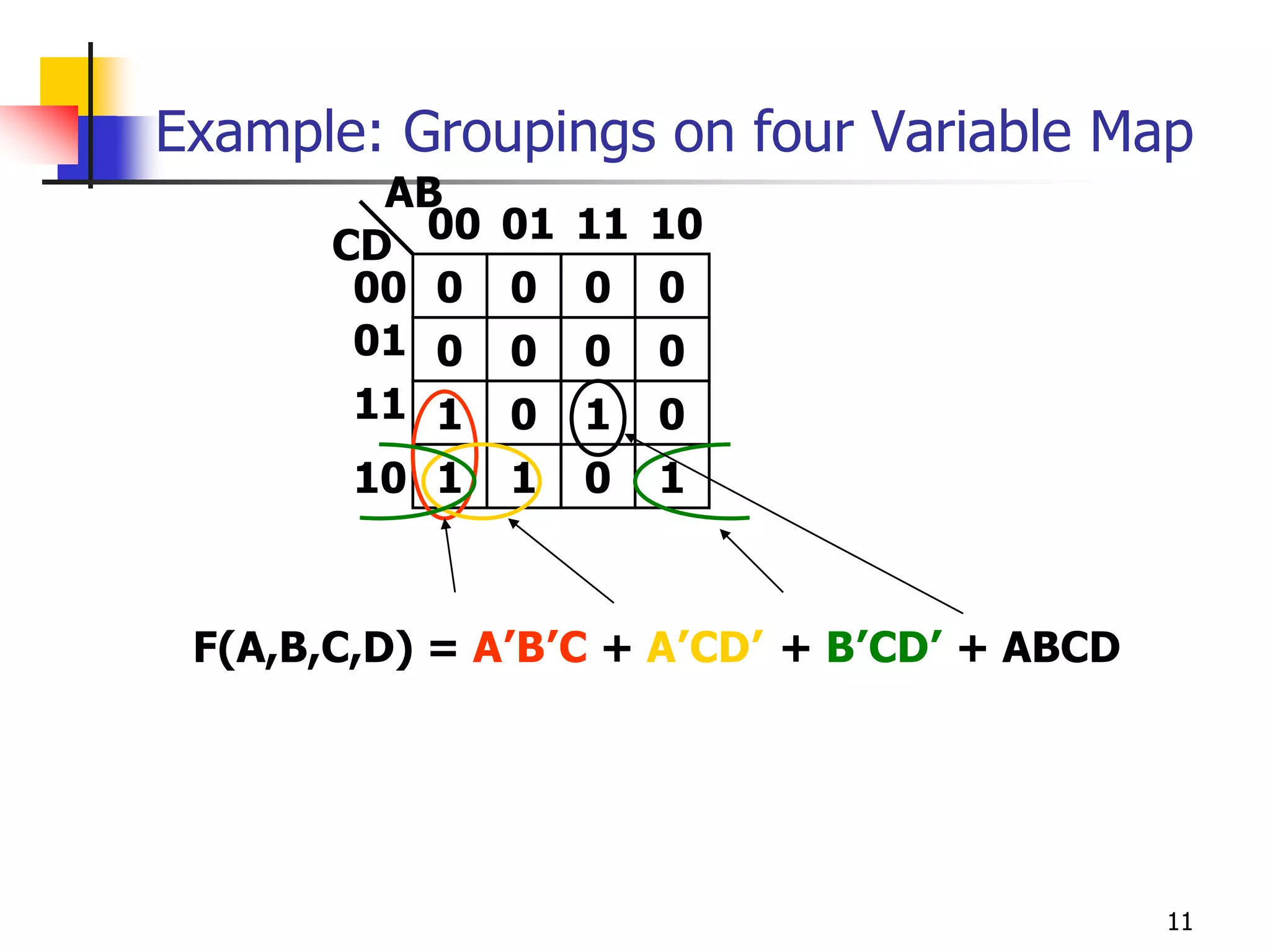
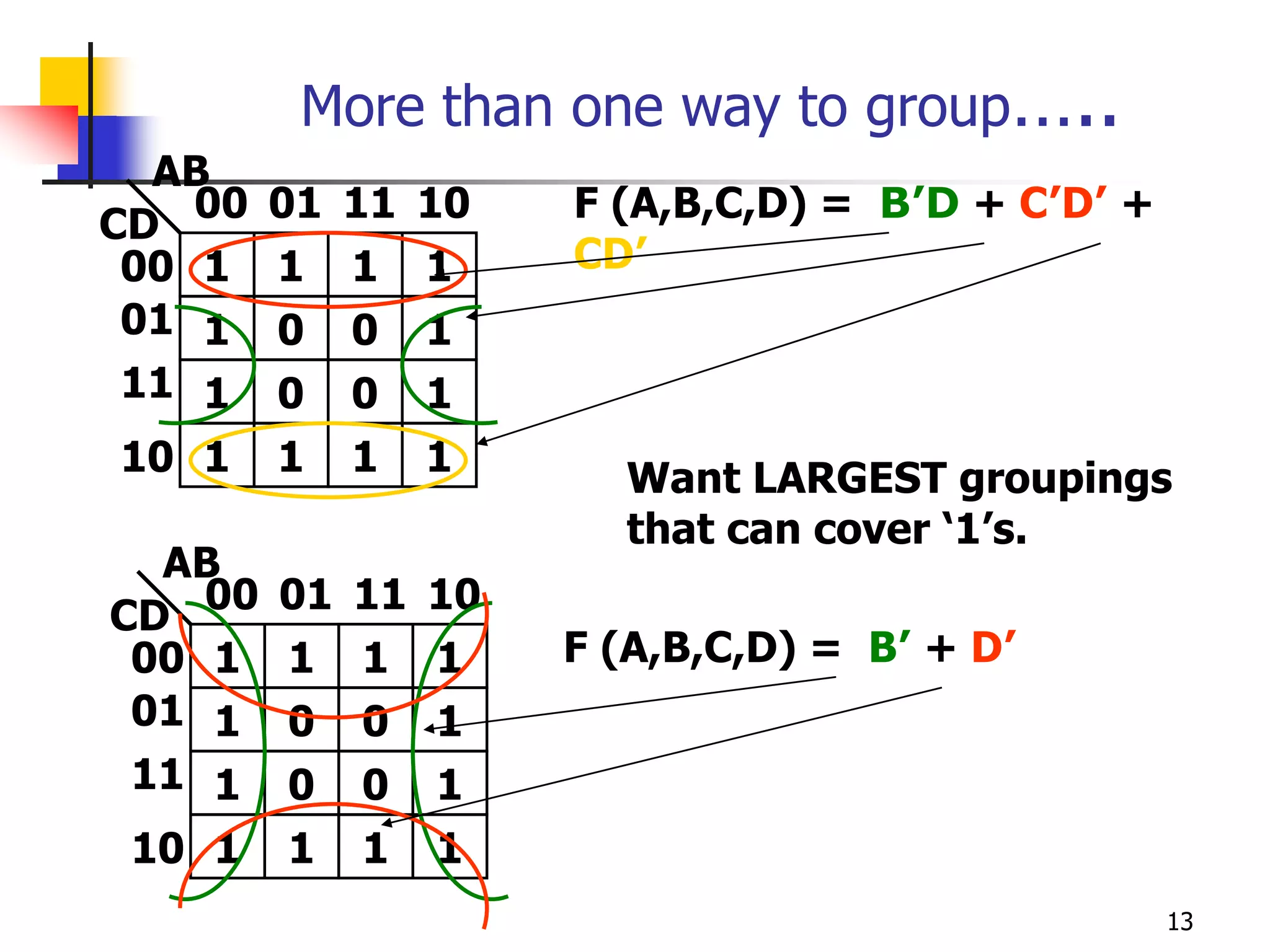
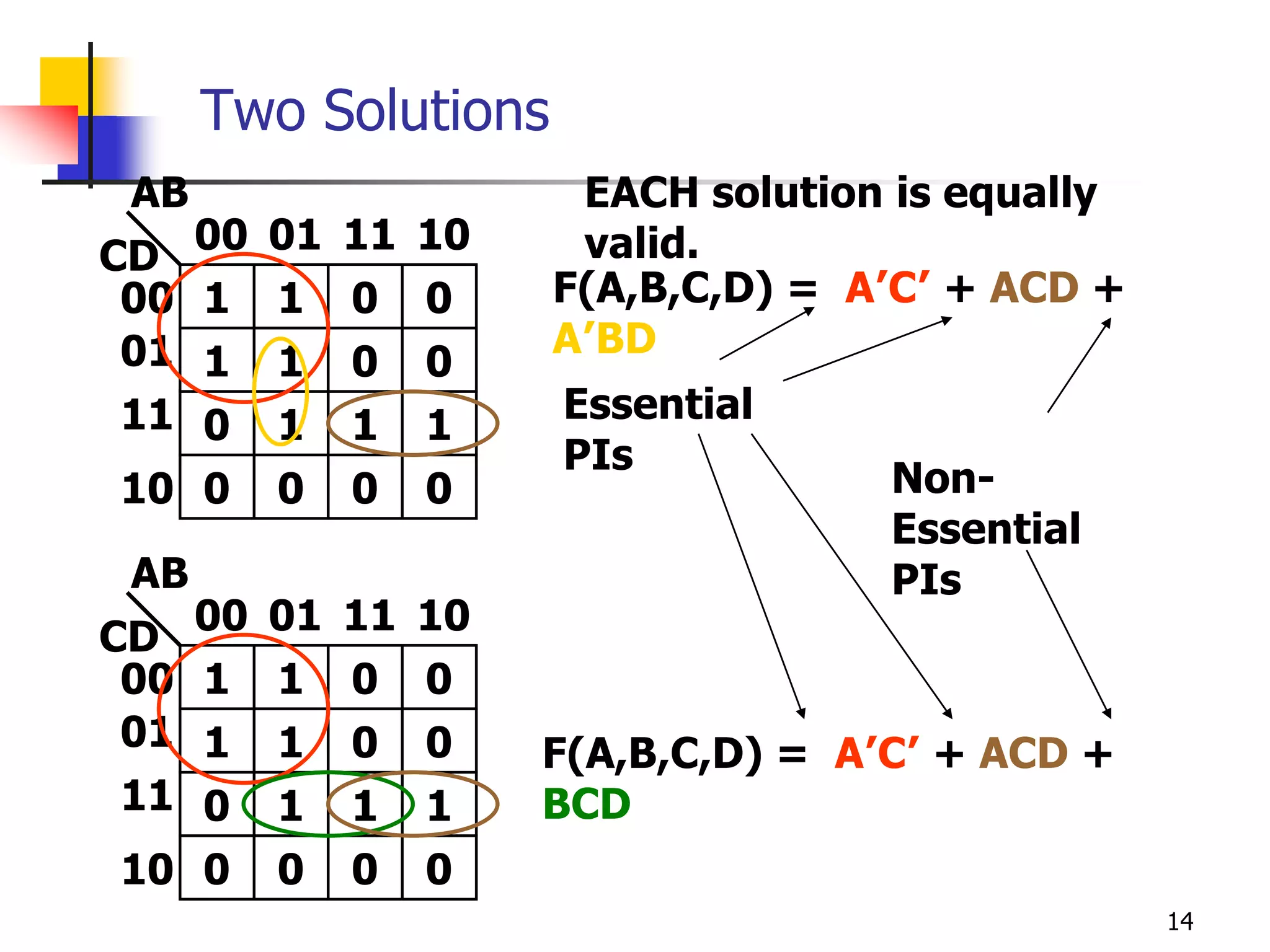
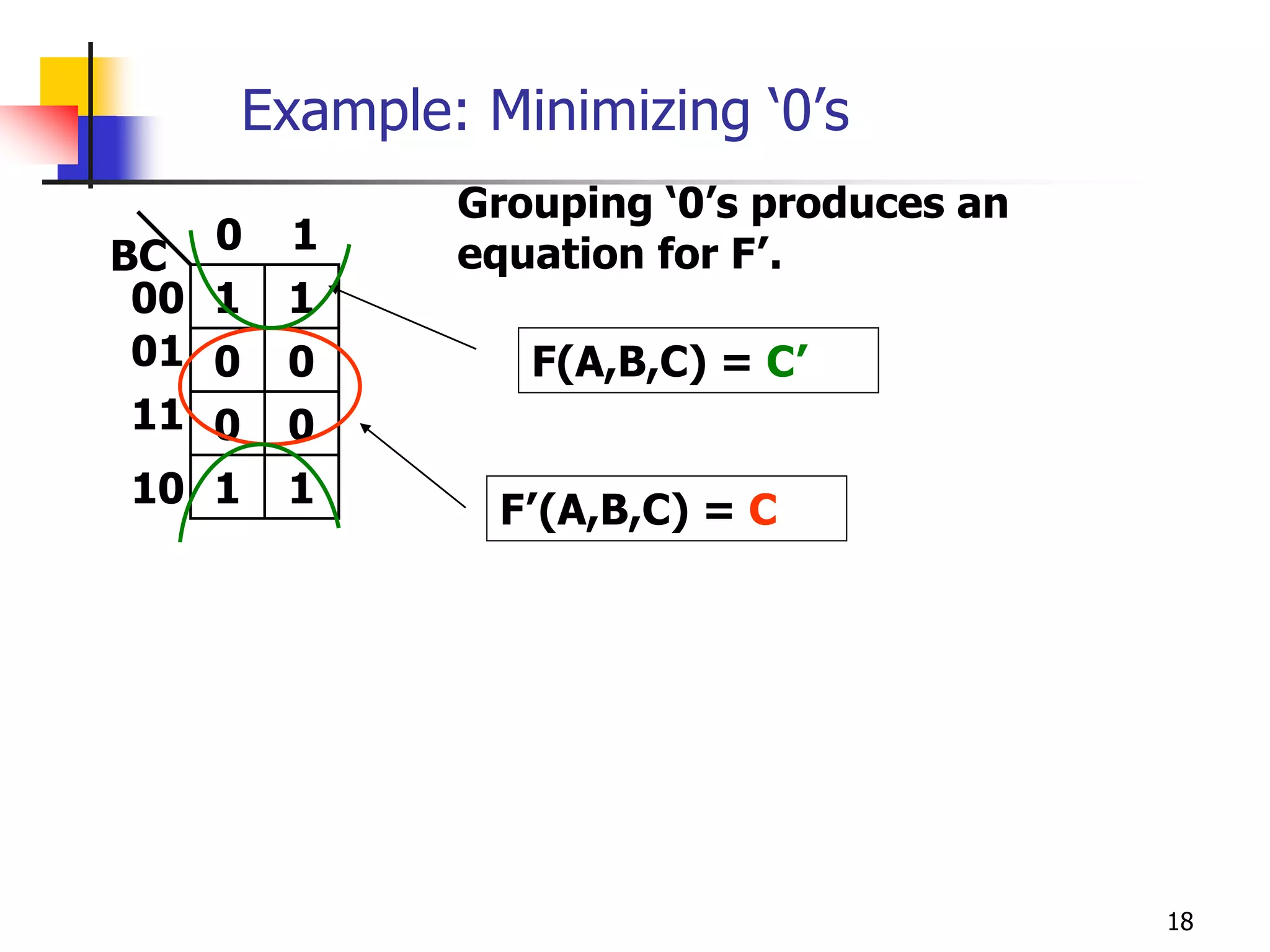
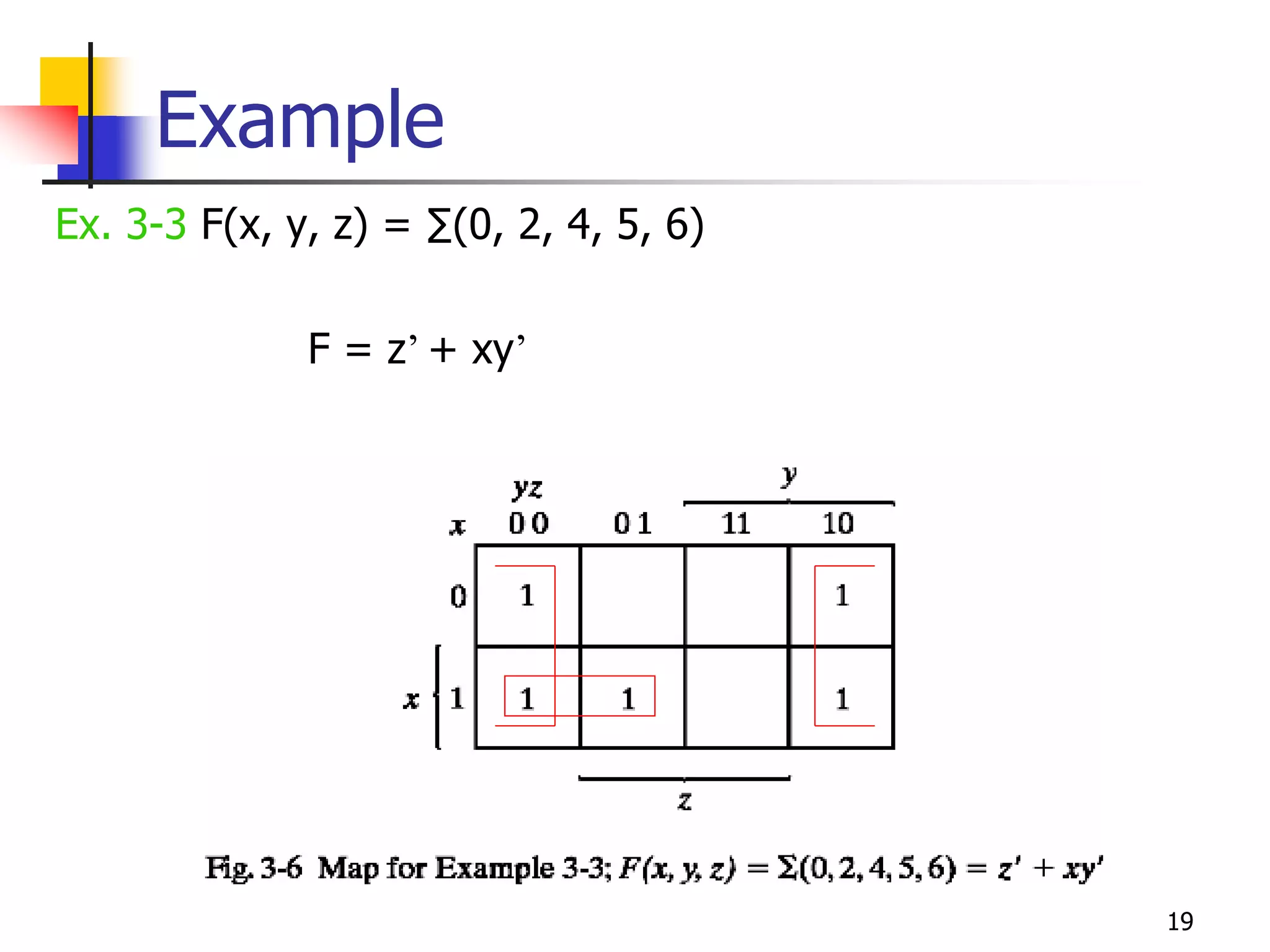
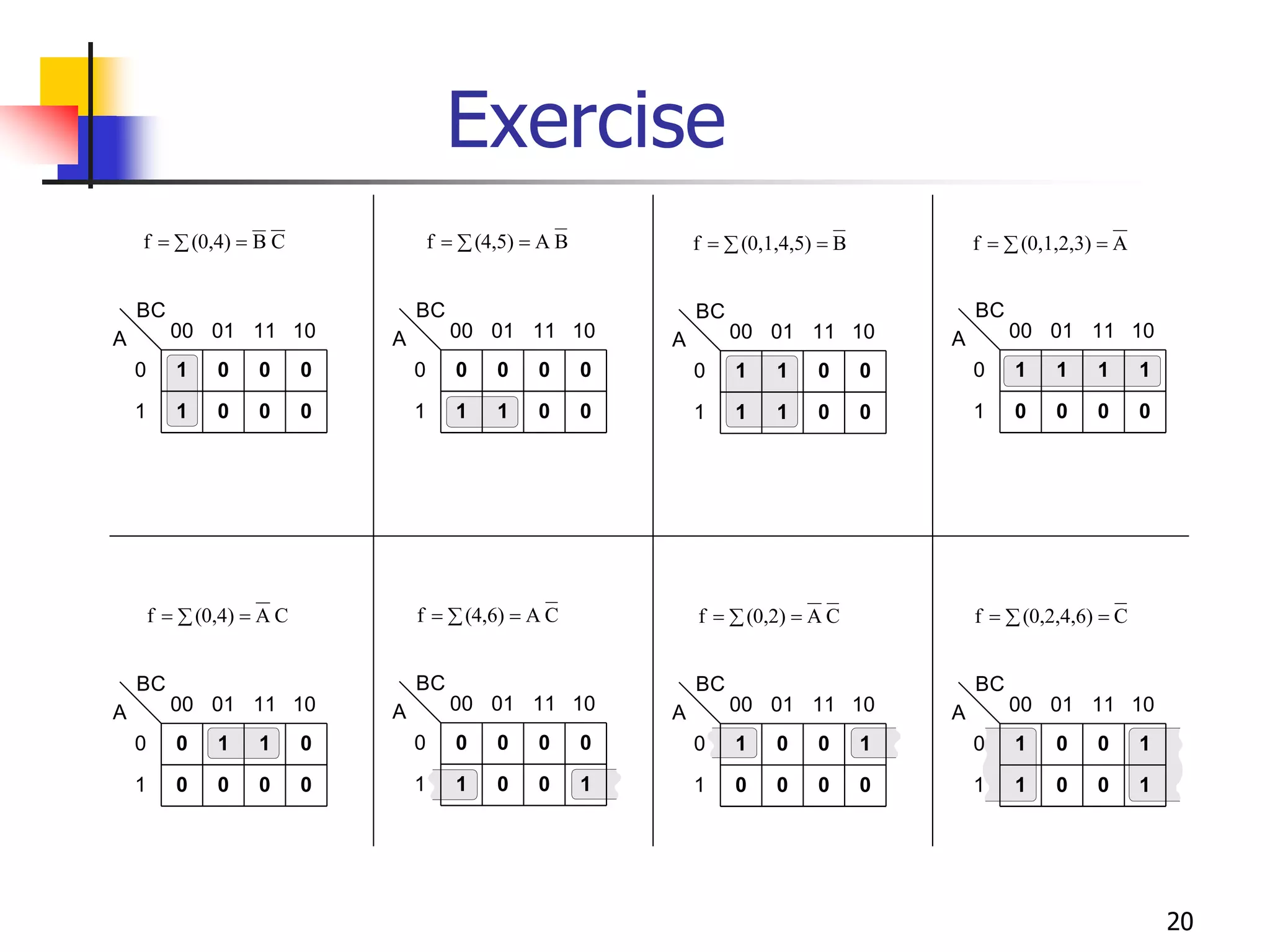
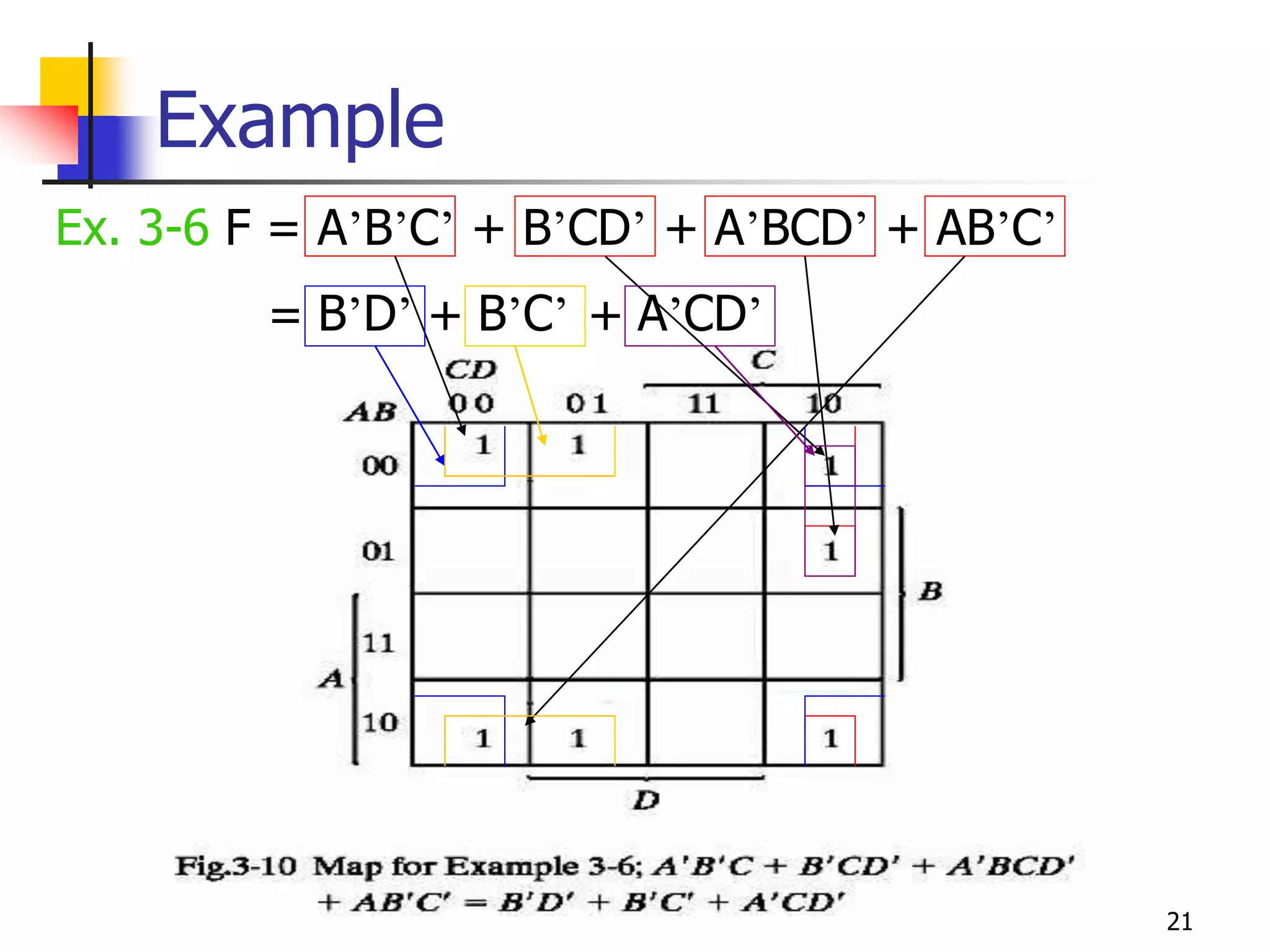
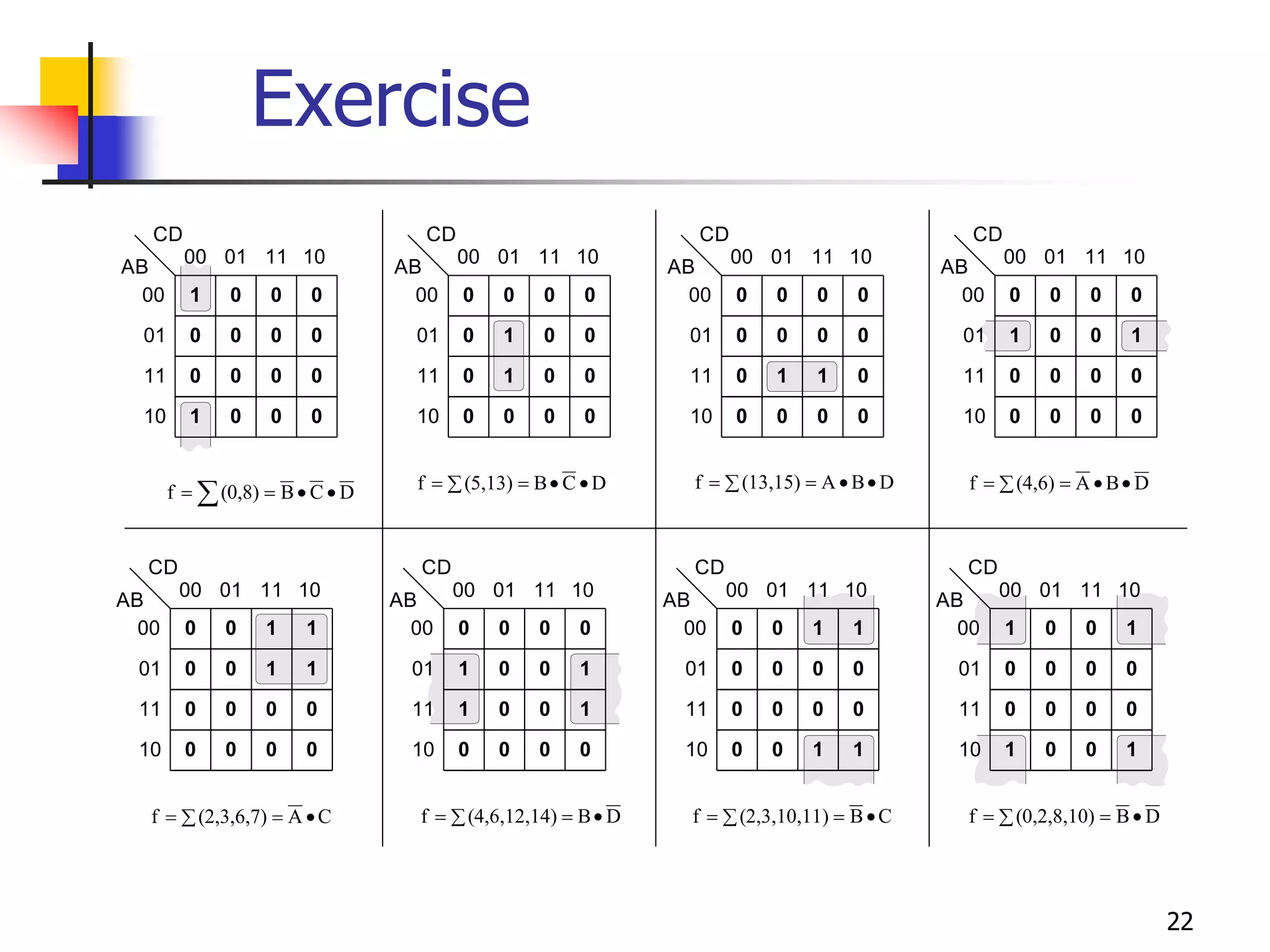
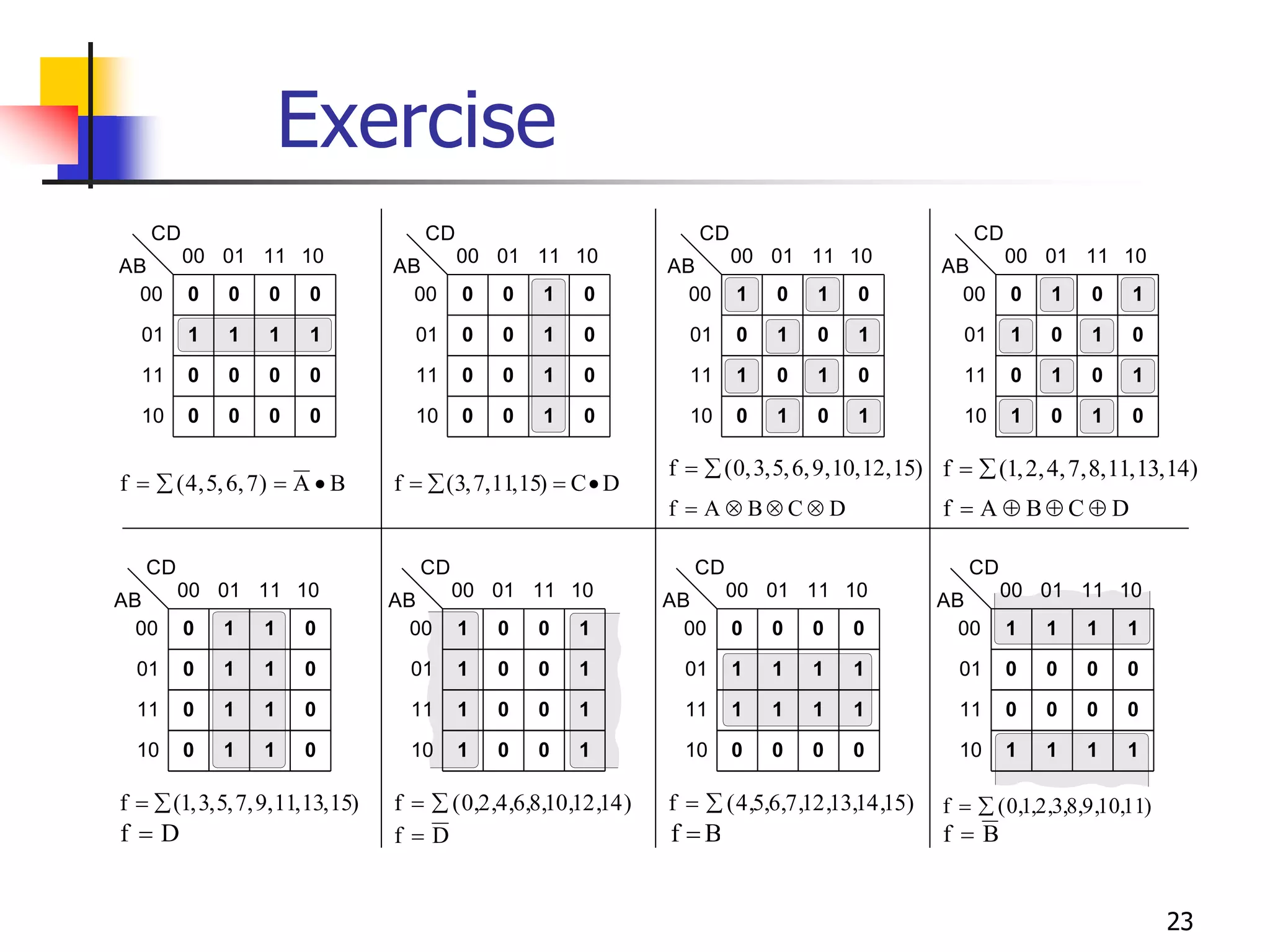
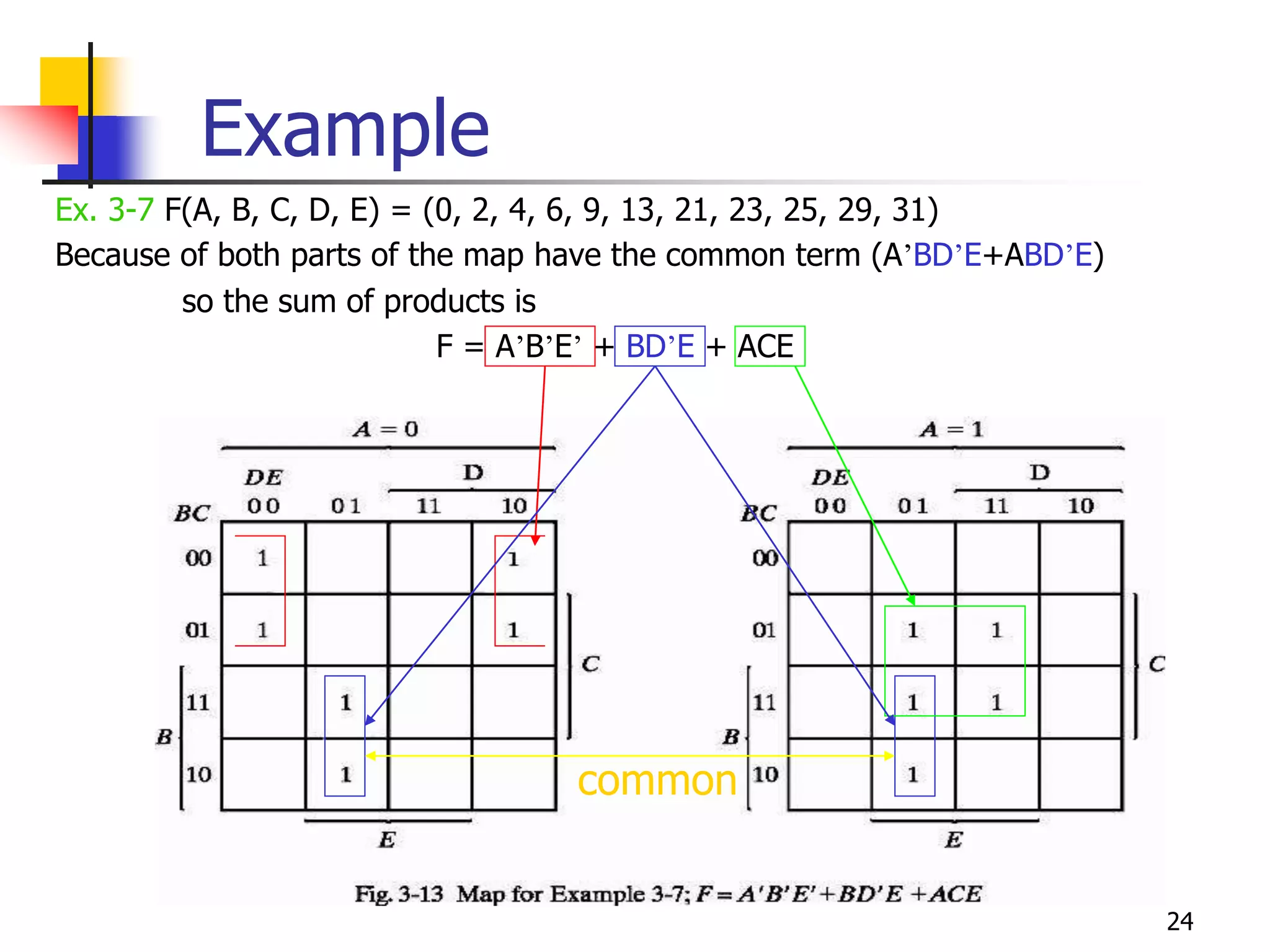
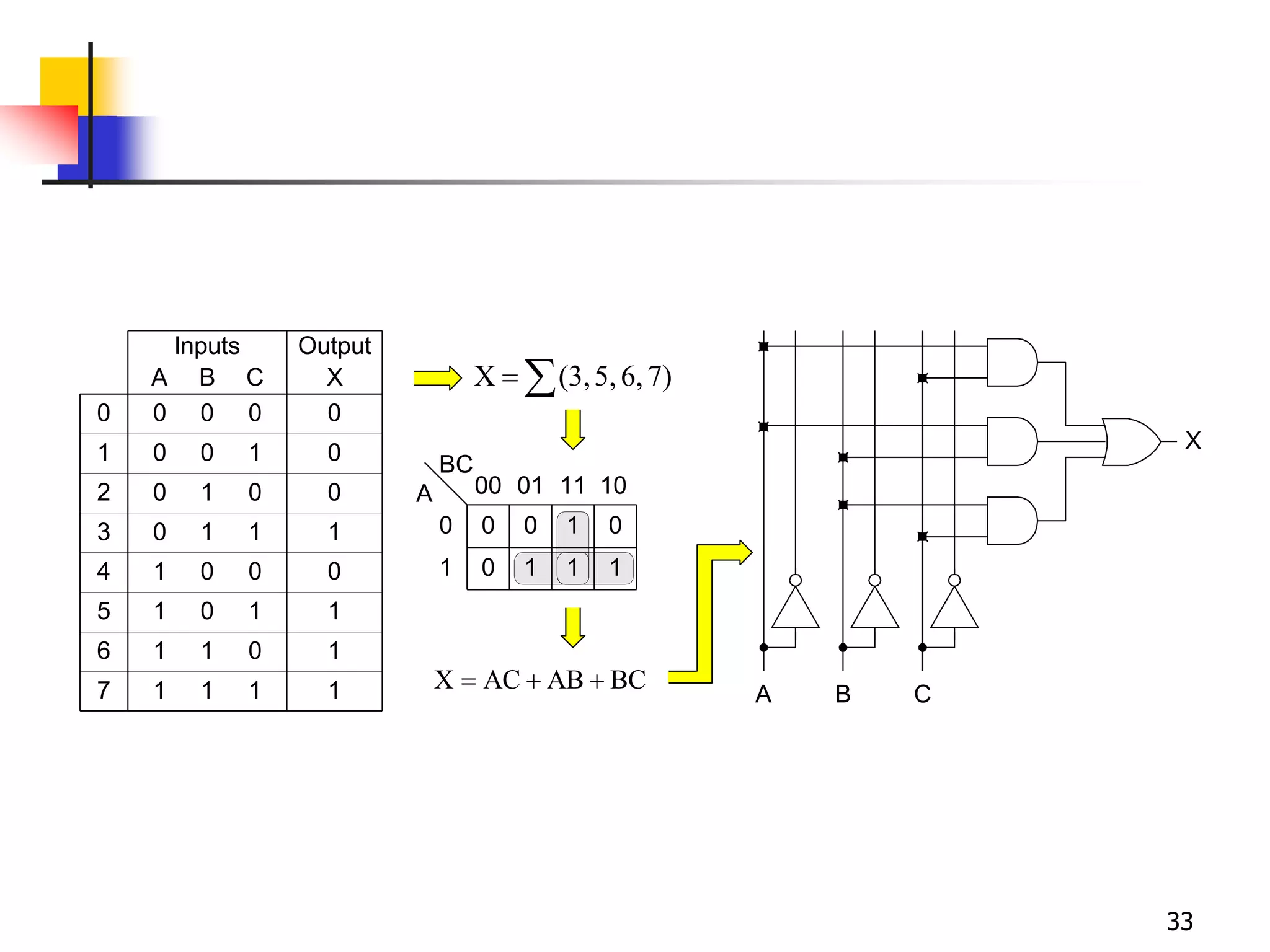
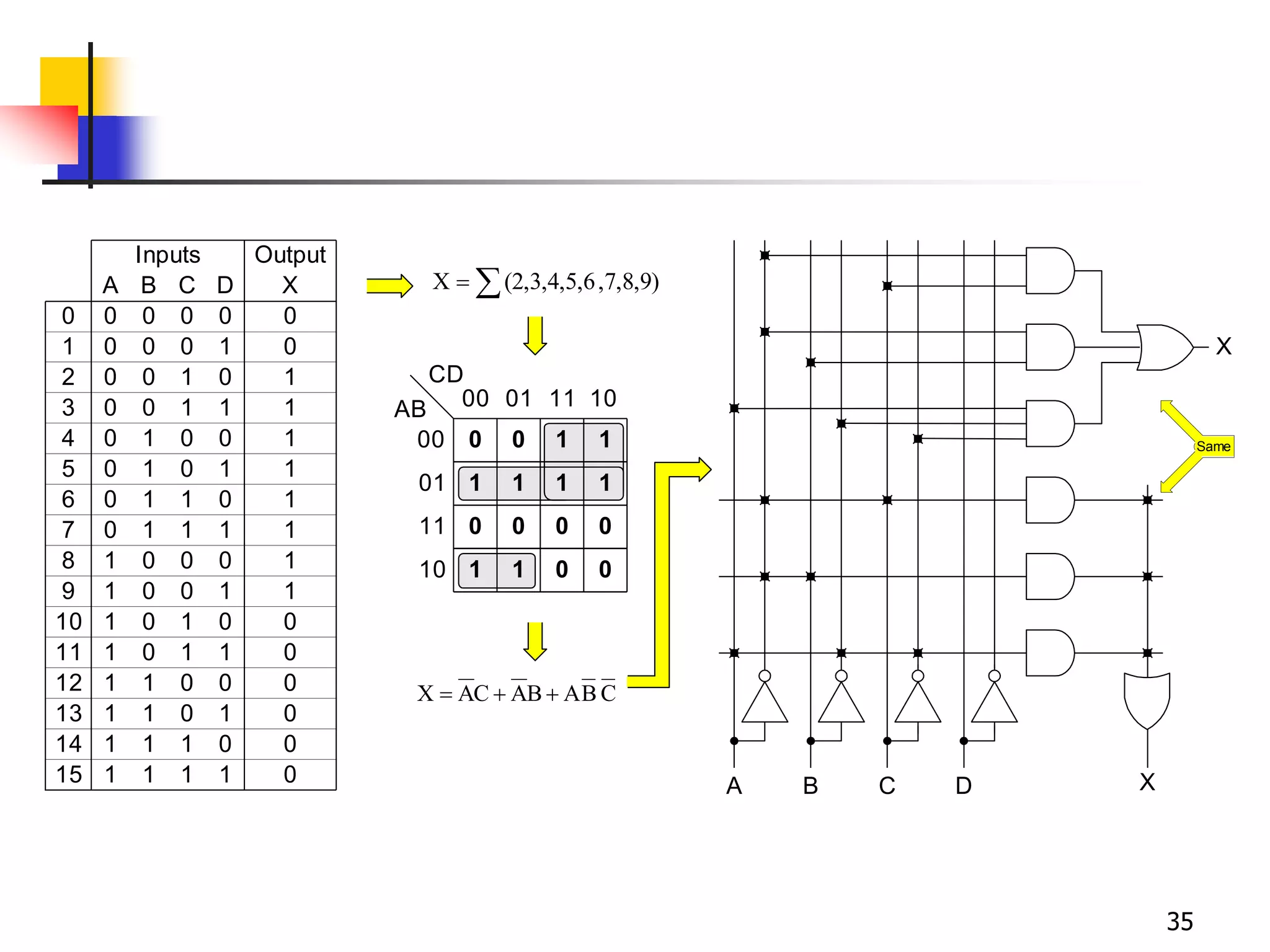
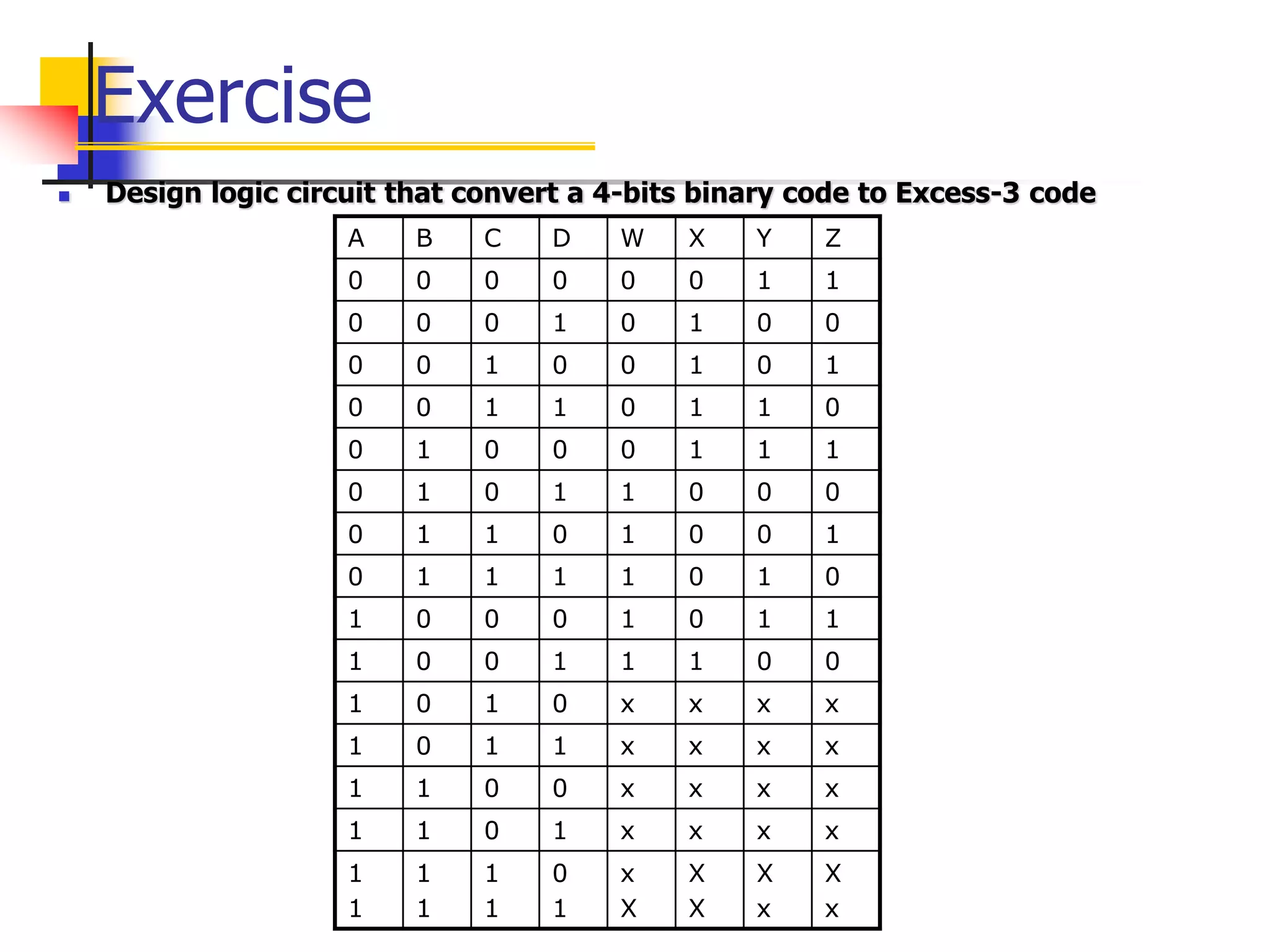
Karnaugh maps are a graphical method used to minimize logic functions. They arrange the minterms of a function in a grid based on the number of variables. Groupings of adjacent 1s in the map correspond to simplified logic terms. The largest possible groupings are used to find a minimum logic expression for the function. Don't cares can also be grouped and treated as 0s or 1s to further simplify expressions.

1. 1
Chapter 3 Gate-Level
Minimization
 A Karnaugh map is a graphical method used to
obtained the most simplified form of an expression
in a standard form (Sum-of-Products or Product-of-
Sums
 The map is made up of squares, with each square
representing one minterm of the function.
 This produces a circuit diagram with a minimum
number of gates and the minimum number of
inputs to the gate.
 It is sometimes possible to find two or more
expressions that satisfy the minimization criteria.

2. What are Karnaugh1 maps?
 Karnaugh maps provide an alternative way of
simplifying logic circuits.
 Instead of using Boolean algebra simplification
techniques, you can transfer logic values from a
Boolean statement or a truth table into a Karnaugh
map.
 The arrangement of 0's and 1's within the map
helps you to visualise the logic relationships
between the variables and leads directly to a
simplified Boolean statement.
1Named for the American electrical engineer Maurice Karnaugh.

3. Karnaugh maps
 Karnaugh maps, or K-maps, are often used to simplify logic problems
with 2, 3 or 4 variables.
B
A
For the case of 2 variables, we form a map consisting
of 22=4 cells as shown in Figure
A
B 0 1
0
1
Cell = 2n ,where n is a number of variables
00 10
01 11
A
B 0 1
0
1
A
B 0 1
0
1
B
A
B
A AB
B
A B
A 
B
A B
A 
Maxterm Minterm
0 2
1 3

4. Karnaugh maps
 3 variables Karnaugh map
AB
C 00 01 11 10
0
1
C
B
A C
B
A C
AB C
B
A
C
B
A BC
A ABC C
B
A
0 1 3 2
6
5
4 7
Cell = 23=8

5. Karnaugh maps
 4 variables Karnaugh map
AB
CD 00 01 11 10
00
01
11
10
5
12
4
13
9
8
0 1
6
15
7
14
10
11
3 2

6. 6
Five-variable map
 Fig.3-12, the left-hand four-variable map represents the 16 squares
where A=0, and the other four-variable map represents the squares
where A=1.
 In addition, each square in the A=0 map is adjacent to the
corresponding square in the A=1 map.

7.  The Karnaugh map is completed by entering a
'1‘(or ‘0’) in each of the appropriate cells.
 Within the map, adjacent cells containing 1's (or
0’s) are grouped together in twos, fours, or
eights.
Karnaugh maps

8. 8
Example: Groupings on 3-Variable K-Maps
1
1 0
1 0
00
BC
0
0 0
0 0
01
11
10
F(A,B,C) = A’B’
A
1
1 1
1 1
00
BC
0
0 0
0 0
01
11
10
F(A,B,C) = B’
A
1
1 1
0 0
00
BC
0
0 0
1
01
11
10
F(A,B,C) = C’
1
Remember that
top and bottom
of map are
adjacent

9. 9
Example: Multiple Groupings
1
1 0
1 1
00
BC
0
0 0
0 0
01
11
10
Want to cover all ‘1’s with
largest possible
groupings.
F(A,B,C) = B’C + A’B’
1
0 1
0 0
00
BC
0
1 0
1 0
01
11
10
Groupings of only a single ‘1’
are ok if larger groupings
cannot be found.
F(A,B,C) = AB’C’ + A’B
A
A

10. 10
Illegal Groupings
1
1 0
0 1
00
BC
0
0 0
0 0
01
11
10
A
Illegal Grouping!
Minterms are not boolean
adjacent!
A’B’C’ , AB’C will NOT reduce
to a single product term
A’B’C’ + AB’C = B’(A’C’+AC)
Valid groupings will always be a power of 2.
(will cover 1, 2, 4, 8, etc. minterms).

11. 11
Example: Groupings on four Variable Map
AB
01
0 0
0 0
00
CD
00
1 0
1 1
01
11
10
0 0
0 0
1 0
0 1
11 10
F(A,B,C,D) = A’B’C + A’CD’ + B’CD’ + ABCD

12. 12
AB
01
1 0
1 0
00
CD
00
1 0
1 0
01
11
10
0 1
0 1
0 1
0 1
11 10
F (A,B,C,D) = B’
Example: Groupings on four Variable Map

13. 13
More than one way to group…..
AB
01
1 1
1 0
00
CD
00
1 0
1 1
01
11
10
1 1
0 1
0 1
1 1
11 10 F (A,B,C,D) = B’D + C’D’ +
CD’
AB
01
1 1
1 0
00
CD
00
1 0
1 1
01
11
10
1 1
0 1
0 1
1 1
11 10
F (A,B,C,D) = B’ + D’
Want LARGEST groupings
that can cover ‘1’s.

14. 14
Two Solutions
AB
01
1 1
1 1
00
CD
00
0 1
0 0
01
11
10
0 0
0 0
1 1
0 0
11 10
EACH solution is equally
valid.
F(A,B,C,D) = A’C’ + ACD +
A’BD
AB
01
1 1
1 1
00
CD
00
0 1
0 0
01
11
10
0 0
0 0
1 1
0 0
11 10
F(A,B,C,D) = A’C’ + ACD +
BCD
Essential
PIs
Non-
Essential
PIs

15. Don't Care Conditions
 There may be a combination of input values which
 will never occur
 if they do occur, the output is of no concern.
 The function value for such combinations is called a
don't care.
 They are denoted with x or –. Each x may be
arbitrarily assigned the value 0 or 1 in an
implementation.
 Don’t cares can be used to further simplify a
function
2023/1/18 Boolean Algebra PJF - 15

16. 16
Example: Don’t Cares
Recall that Don’t
Cares are labeled as
‘X’s in truth table.
Can treat X’s as
either ‘0’s or ‘1’s
Row A B C D F(A,B,C,D)
0 0 0 0 0 0
1 0 0 0 1 0
2 0 0 1 0 1
3 0 0 1 1 1
4 0 1 0 0 0
5 0 1 0 1 0
6 0 1 1 0 1
7 0 1 1 1 0
8 1 0 0 0 0
9 1 0 0 1 0
10 1 0 1 0 x
11 1 0 1 1 x
12 1 1 0 0 x
13 1 1 0 1 x
14 1 1 1 0 x
15 1 1 1 1 x
F(ABCD)
Recognize BCD
numbers: 2,3,6
A
B
C
D
Non-BCD numbers are
don’t cares because will
never be applied as
inputs.
F

17. 17
Don’t Cares treated as ‘0’s or ‘1’s
AB
01
0 0
0 0
00
CD
00
1 0
1 1
01
11
10
X 0
X 0
X X
X X
11 10
Treat X’s as 1’s when
can get a larger
grouping. (Not all
X’s need to be
covered.)
F(A,B,C,D) = CD’ + B’C

18. 18
Example: Minimizing ‘0’s
1
1 1
0 0
00
BC
0
0 0
1
01
11
10
F(A,B,C) = C’
1
Grouping ‘0’s produces an
equation for F’.
F’(A,B,C) = C

19. 19
Example
Ex. 3-3 F(x, y, z) = ∑(0, 2, 4, 5, 6)
F = z’ + xy’

20. Exercise
20
 
 C
B
(0,4)
f  
 B
A
(4,5)
f  
 B
(0,1,4,5)
f  
 A
(0,1,2,3)
f
BC
00
0
01
1
11 10
A
1 0 0 0
1 0 0 0
BC
00
0
01
1
11 10
A
0 0 0 0
1 1 0 0
BC
00
0
01
1
11 10
A
1 1 1 1
0 0 0 0
BC
00
0
01
1
11 10
A
1 1 0 0
1 1 0 0
 
 C
A
(0,4)
f  
 C
A
(4,6)
f  
 C
A
(0,2)
f  
 C
(0,2,4,6)
f
BC
00
0
01
1
11 10
A
0 1 1 0
0 0 0 0
BC
00
0
01
1
11 10
A
0 0 0 0
1 0 0 1
BC
00
0
01
1
11 10
A
1 0 0 1
1 0 0 1
BC
00
0
01
1
11 10
A
1 0 0 1
0 0 0 0

21. 21
Example
Ex. 3-6 F = A’B’C’ + B’CD’ + A’BCD’ + AB’C’
= B’D’ B’C’
+ A’CD’
+

22. Exercise
22
 


 D
C
B
(0,8)
f  


 D
C
B
(5,13)
f  


 D
B
A
(13,15)
f  


 D
B
A
(4,6)
f
 

 C
A
(2,3,6,7)
f  

 D
B
)
(4,6,12,14
f  

 C
B
)
(2,3,10,11
f  

 D
B
(0,2,8,10)
f
CD
00
00
01
01
11
11
10
10
AB
1 0 0 0
0 0 0 0
0 0 0 0
1 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
0 1 0 0
0 1 0 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
0 0 0 0
0 1 1 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
1 0 0 1
0 0 0 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 1 1
0 0 1 1
0 0 0 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
1 0 0 1
1 0 0 1
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 1 1
0 0 0 0
0 0 0 0
0 0 1 1
CD
00
00
01
01
11
11
10
10
AB
1 0 0 1
0 0 0 0
0 0 0 0
1 0 0 1

23. Exercise
23
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
1 1 1 1
0 0 0 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 1 0
0 0 1 0
0 0 1 0
0 0 1 0
CD
00
00
01
01
11
11
10
10
AB
1 0 1 0
0 1 0 1
1 0 1 0
0 1 0 1
CD
00
00
01
01
11
11
10
10
AB
0 1 0 1
1 0 1 0
0 1 0 1
1 0 1 0
CD
00
00
01
01
11
11
10
10
AB
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
CD
00
00
01
01
11
11
10
10
AB
1 0 0 1
1 0 0 1
1 0 0 1
1 0 0 1
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
1 1 1 1
1 1 1 1
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
1 1 1 1
0 0 0 0
0 0 0 0
1 1 1 1
f (4,5,6,7) A B
  
 f (3,7,11,15) C D
  

f (0,3,5,6,9,10,12,15)
  f (1,2,4,7,8,11,13,14)
 
f A B C D
    f A B C D
   
f (1,3,5,7,9,11,13,15)
  f (0,2,4,6,8,10,12,14)
  f (4,5,6,7,12,13,14,15)
  f (0,1,2,3,8,9,10,11)
 
f D
 f D
 f B
 f B


24. 24
Example
Ex. 3-7 F(A, B, C, D, E) = (0, 2, 4, 6, 9, 13, 21, 23, 25, 29, 31)
Because of both parts of the map have the common term (A’BD’E+ABD’E)
so the sum of products is
F = A’B’E’ + BD’E + ACE
common

25. 25
3-5. Don’t care conditions
Ex.3-9 Simplify the F (w, x, y, z)= ∑(1, 3, 7, 11, 15) with
don’t-care conditions d(w, x, y, z) = ∑(0, 2, 5)
In part (a) with minterms 0 and 2 F = yz + w’x’
In part (b) with minterm 5  F = yz + w’z

26. Example Don’t care
 Simplify the function f(a,b,c,d)
whose K-map is shown at the
right.
 f = a’c’d+ab’+cd’+a’bc’
or
 f = a’c’d+ab’+cd’+a’bd’
2023/1/18 Boolean Algebra PJF - 26
x
x
1
1
x
x
0
0
1
0
1
1
1
0
1
0
x
x
1
1
x
x
0
0
1
0
1
1
1
0
1
0
0 1 0 1
1 1 0 1
0 0 x x
1 1 x x
ab
cd
00
01
11
10
00 01 11 10

27. Another Example
 Simplify the function
g(a,b,c,d) whose K-map
is shown at right.
 g = a’c’+ ab
or
 g = a’c’+b’d
2023/1/18 Boolean Algebra PJF - 27
x 1 0 0
1 x 0 x
1 x x 1
0 x x 0
x 1 0 0
1 x 0 x
1 x x 1
0 x x 0
x 1 0 0
1 x 0 x
1 x x 1
0 x x 0
ab
cd

28. 28
3-4. Product of sums
simplification
 If we mark the empty squares by 0’s rather than
1’s and combine them into valid adjacent squares,
we obtain the complement of the function, F’. Use
the DeMorgan’s theorem, we can get the product
of sums.
Ex.3-8 Simplify the Boolean function in
(a) sum of products
(b) product of sums
F(A, B, C, D) = ∑(0, 1, 2, 5, 8, 9, 10)

29. 29
Example
(a) SOPs
F=
(b) POSs
F’=
By DeMorgan’s thm
F=
B’D’+ B’C’+ A’C’D
AB + CD + BD’
(A’+B’) .(C’+D’)
.(B’+D)

30. 30
Example: Group 0’s, then Complement to
get POS
AB
01
0 0
0 0
00
CD
00
1 0
1 1
01
11
10
X 0
X 0
X X
X X
11 10
F’(A,B,C,D) = C’ + BD
Take inverse of both sides
F(A,B,C,D) = (C’ + BD)’
= C (BD)’
= C (B’+D’)
Grouping zeros, then applying inverse to both
sides is a way to get to minimum POS form

31. 31
Exchange minterm and maxterm
 Consider the truth table
that defines the function F
in Table 3-2.
Sum of minterms
F(x, y, z) = ∑(1, 3, 4, 6)
Product of maxterms
F(x, y, z) = ∏(0, 2, 5, 7)
 In the other words, the 1’s
of the function represent
the minterms, and the 0’s
represent the maxterms.

32. Practice 1:Combinational circuit Design
 Example: Design a 3-input (A,B,C) digital
circuit that will give at its output (X) a logic 1
only if the binary number formed at the
input has more ones than zeros.
32

33. 33
BC
AB
AC
X 


A B C
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
X
0
0
0
1
0
1
1
1
Inputs Output
0
1
2
3
4
5
6
7
BC
00
0
01
1
11 10
A
0 0 1 0
0 1 1 1
A B C
X

 7)
6,
5,
(3,
X

34. Practice 2:Combinational circuit Design
34
 Example: Design a 4-input (A,B,C,D) digital circuit that will give at its
output (X) a logic 1 only if the binary number formed at the input is
between 2 and 9 (including).

35. 35
C
B
A
B
A
C
A
X 


A B C
X

 ,7,8,9)
(2,3,4,5,6
X
A B C
0
0
0
0
0
1
X
0
0
Inputs Output
0
1
D
0
0
0 0 0 1
2 1
0 0 1 1
3 1
0 1 0 1
4 0
0 1 1 1
5 0
0 1 0 1
6 1
0 1 1 1
7 1
1 0 0 1
8 0
1 0 1 1
9 0
1 0 0 0
10 1
1 0 1 0
11 1
1 1 0 0
12 0
1 1 1 0
13 0
1 1 0 0
14 1
1 1 1 0
15 1 D
CD
00
00
01
01
11
11
10
10
AB
0 0 1 1
1 1 1 1
0 0 0 0
1 1 0 0
X
Same

36. Exercise
 Design logic circuit that convert a 4-bits binary code to Excess-3 code
A B C D W X Y Z
0 0 0 0 0 0 1 1
0 0 0 1 0 1 0 0
0 0 1 0 0 1 0 1
0 0 1 1 0 1 1 0
0 1 0 0 0 1 1 1
0 1 0 1 1 0 0 0
0 1 1 0 1 0 0 1
0 1 1 1 1 0 1 0
1 0 0 0 1 0 1 1
1 0 0 1 1 1 0 0
1 0 1 0 x x x x
1 0 1 1 x x x x
1 1 0 0 x x x x
1 1 0 1 x x x x
1
1
1
1
1
1
0
1
x
X
X
X
X
x
X
x