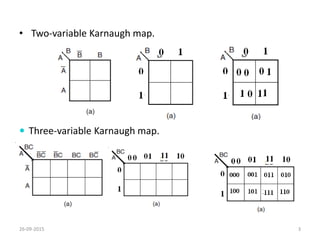
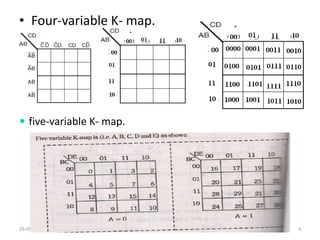
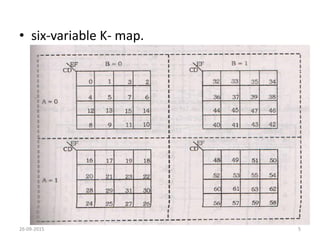
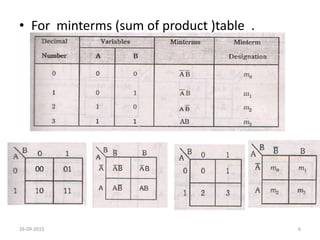
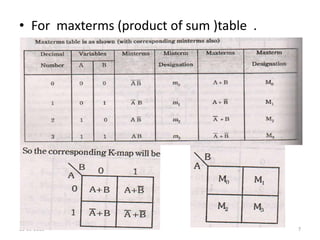
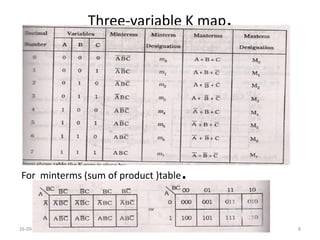
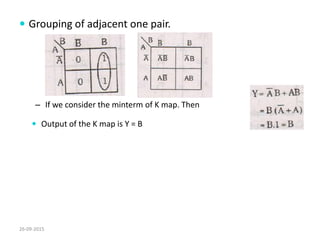
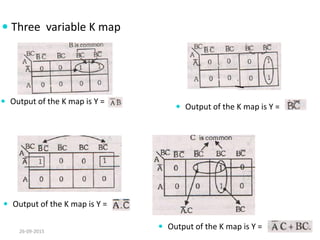
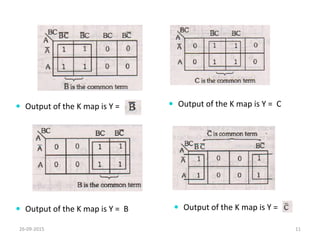
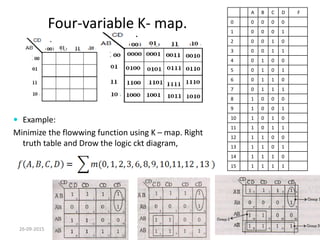
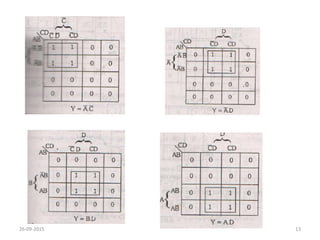
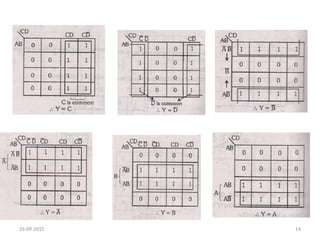
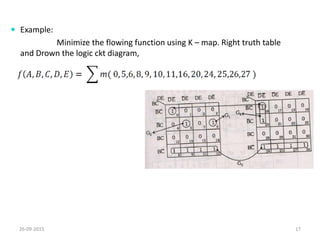
A Karnaugh map is a graphical representation of a logic system that can be used to minimize sum-of-products or product-of-sums Boolean expressions. It works by plotting the minterms or maxterms of a function onto a grid whose dimensions correspond to the number of variables. Ones are placed in the cells that correspond to true minterms or false maxterms, while don't cares are marked with Xs. By grouping adjacent ones, the Karnaugh map allows identifying logical patterns to minimize the expression into prime implicants. The document provides examples of two, three, and four variable Karnaugh maps and discusses their use case for minimization.

1. Karnaugh Maps(K- Map)
• A Karnaugh map is a graphical representation of the logic system.
• It can be drawn directly from either minterm (sum-of-products) or
maxterm (product-of-sums) Boolean expressions
• It is desired to have a minimized sum-of-products or a minimized
product-of-sums expression.
26-09-2015 1
 Types of K- Map
 Two-variable Karnaugh map.

2. • Construction of a Karnaugh Map(K- Map)
26-09-2015 2
 An n-variable Karnaugh map has 2n squares
 In the case of a minterm Karnaugh map,
 ‘1’ is placed in all those squares for which the output is ‘1’,
 ‘0’ is placed in all those squares for which the output is ‘0’. 0s are omitted for
simplicity.
 An ‘X’ is placed in squares corresponding to ‘don’t care’
conditions.
 In the case of a maxterm Karnaugh map,
 ‘1’ is placed in all those squares for which the output is ‘0’,
 ‘0’ is placed for input entries corresponding to a ‘1’ output. Again, 0s
are omitted for simplicity,
 an ‘X’ is placed in squares corresponding to ‘don’t care’ conditions.

3. • Two-variable Karnaugh map.
26-09-2015 3
 Three-variable Karnaugh map.

4. • Four-variable K- map.
26-09-2015 4
 five-variable K- map.

5. • six-variable K- map.
26-09-2015 5

6. 26-09-2015 6
• For minterms (sum of product )table .

7. 26-09-2015 7
• For maxterms (product of sum )table .

8. Three-variable K map.
26-09-2015 8
For minterms (sum of product )table.

9. 26-09-2015
– If we consider the minterm of K map. Then
 Grouping of adjacent one pair.
 Output of the K map is Y = B

10. 26-09-2015
 Output of the K map is Y =
 Output of the K map is Y =
 Three variable K map
 Output of the K map is Y =
 Output of the K map is Y =

11. 26-09-2015 11
 Output of the K map is Y =  Output of the K map is Y = C
 Output of the K map is Y = B  Output of the K map is Y =

12. Four-variable K- map.
26-09-2015 12
A B C D F
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
10 1 0 1 0
11 1 0 1 1
12 1 1 0 0
13 1 1 0 1
14 1 1 1 0
15 1 1 1 1
 Example:
Minimize the flowwing function using K – map. Right
truth table and Drow the logic ckt diagram,

13. 26-09-2015 13

14. 26-09-2015 14

15. 26-09-2015 15
 Example:
Minimize the flowing function using K – map. Right truth
table and Drown the logic ckt diagram,

16. Five-variable K- map.
26-09-2015 16
 Example:
Minimize the flowing function using K – map. Right truth table
and Drown the logic ckt diagram,

17. 26-09-2015 17
 Example:
Minimize the flowing function using K – map. Right truth table
and Drown the logic ckt diagram,