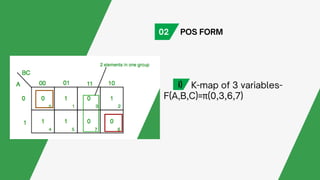
The document discusses Karnaugh maps (k-maps), a graphical tool used for simplifying boolean expressions with benefits including ease of data representation and straightforward implementation. It outlines the properties, operations, and simplification processes involved in solving k-maps for both sum of products (SOP) and product of sums (POS) forms. Additionally, it touches on the 'don't care' condition, which can aid in further simplification.

1. Spooky Peeps
Karnaugh Map (K-map)

2. MD. SAKIBUZZAMAN ALIF
201-15-3339
Ahmed Ishtiak Nihal
201-15-3277
MD SAIMUR RAHMAN SWARNAB
201-15-3303
Nur-A-Alam Siddiqi
201-15-3274
TEAM MEMBERS

3. Introduction
The Karnaugh map (K-map) is a two-
dimensional variant of the truth table,
designed in such a way as the simplification
of a Boolean expression.

4. Advantages of Karnaugh Maps
201-15-3274
Nur-A-Alam Siddiqi SOPS And POPS

5. The ease with which data can be
represented.
Changes in adjacent variables are
immediately visible.
Changes are simple and
straightforward to implement.
Logic gates are less expensive and
there are fewer of them.
Advantages of
Karnaugh Maps

6. The SOP (Sum of Product) expression
represents 1’s.
SOP form such as (A.B)+(B.C).
The POS (Product of Sum) expression
represents the low (0) values in the K-
Map.
POS form like (A+B). (C+D)
SOP &
POS

7. Properties
201-15-3303
MD Saimur Rahman Swarnab
Simplification Process
How to solve the Karenaugh
map?

8. Properties
An n-variable K-map has 2n cells
with n-variable truth table value.
Adjacent cells differ in only one
bit.
Each cell refers to a minterm or
maxterm.
For minterm mi , maxterm Mi and
don’t care of f we place 1 , 0 , x .

9. Simplification
Process
No diagonals.
Only 2^n cells in each group.
Groups should be as large as
possible.
If all the group cells have the
same set of variables, a group
can be combined.
Overlapping allowed.
The fewest number of groups
possible.

10. How to solve
the
Karenaugh
map?
Sketch a Karnaugh map grid for the
problem.
01
02 Fill in the 1’s and 0’s from the truth table.
03 Circle groups of 1’s.
04 Circle the largest groups of 2, 4, 8,16,32
etc.
05 First Minimize the number of circles but
make sure that every 1 is in a circle.

11. Different Types Of K-Maps
MD.SAKIBUZZAMAN ALIF
201-15-3339

12. SOP FORM
01
K-map of 3 variables-
Z= ∑A,B,C(1,3,6,7)
i)

13. K-map for 4 variables
F(P,Q,R,S)=∑(0,2,5,7,8,10,13,15)
ii)

14. K-map of 3 variables-
F(A,B,C)=π(0,3,6,7)
POS FORM
02
i)

15. K-map of 4 variables-
F(A,B,C,D)=π(3,5,7,8,10,11,12,13)
Finally we express these as product –(C+D’+B’).
(C’+D’+A).(A’+C+D).(A’+B+C’)
ii)

16. Presentation Introduction
201-15-3274
Ahmed Ishtiak Nihal
Don't Care Condition
Conclution

17. Minterms that may produce either 0 or 1 for
the function.
Marked with an ‘x’ in the K-map.
These don’t-care conditions can be used to
provide further simplification.
Don’t-care condition

18. CONCLUSION
Although all advertisements aim to promote or
sell, they come in a wide variety of mediums.
These mediums can be classified as traditional
or digital. Deciding which medium to use
largely depends on the overall advertising
strategy and budget.

19. That's all
about our
presentation