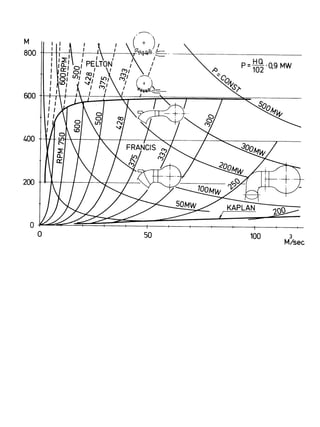
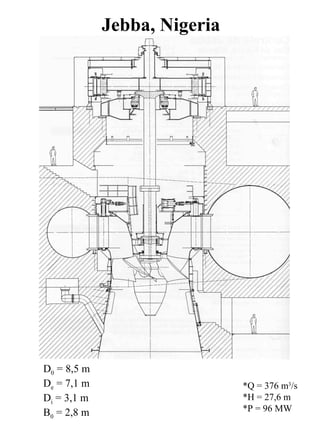
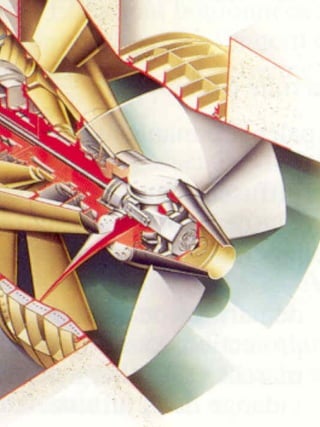
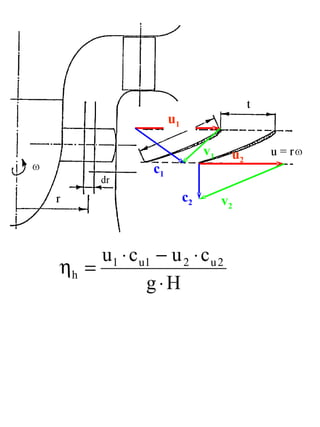
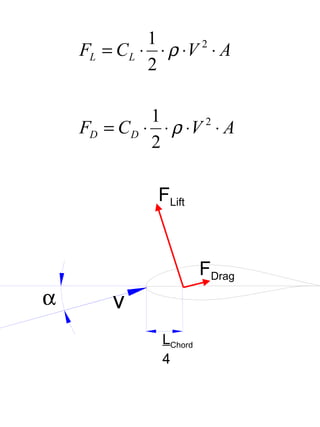
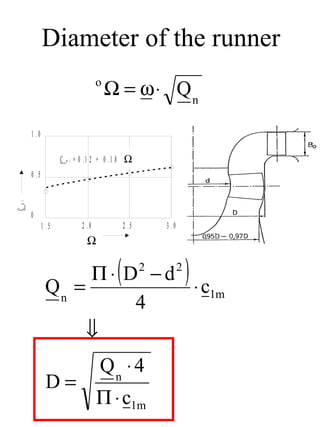
The document provides information on the dimensions and performance of Kaplan turbines, including diagrams showing dimensions such as diameter, blade height and spacing for turbines in Nigeria and Chile. It also contains graphs depicting hydraulic efficiency and cavitation effects in relation to parameters like speed and blade angle. The example calculation at the end demonstrates how to determine the diameter, blade height and number of vanes given design criteria like power output, head and flow rate.

1. Kaplan turbine

3. Jebba, Nigeria
D0 = 8,5 m
De = 7,1 m *Q = 376 m3/s
Di = 3,1 m *H = 27,6 m
B0 = 2,8 m *P = 96 MW

4. Machicura, CHILE
*Q = 144 m3/s
*H = 36,7 m
*P = 48 MW
D0 = 7,2 m
De = 4,2 m
Di = 1,9 m
B0 = 1,3 m

5. Outlet Outlet Inlet Outlet Inlet
draft tube runner runner guide vane guide vane

6. Hydraulic efficiency
Hydraulic efficiency ηh
Runner blade angle
φ = constant
Flow rate Q

8. Hill chart

9. u1
v1 u2
c1
c2 v2
u 1 ⋅ c u1 − u 2 ⋅ c u 2
ηh =
g⋅H

10. Pressure distribution and
torque
c
Lift
Drag
L
Torque
D
Arm

11. 1
FL = C L ⋅ ⋅ ρ ⋅ V ⋅ A
2
2
1
FD = C D ⋅ ⋅ ρ ⋅ V ⋅ A
2
2
FLift
FDrag
α v
LChord
4

12. Blade profile data
CD
CL
Angle of attack
Angle of attack
δ
vv
Average relative
velocity

13. Pressure distribution and
torque
0,24 · l Cord length, l
Suction side
Pressure side
Single profile
Cascade
The pressure at the outlet is lower for a cascade than
for a single profile. The cavitation performance will
therefore be reduced in a cascade.

14. Radial distribution of the
blade profile
CL =Lift coefficient for a cascade
CL1 =Lift coefficient for a single profile
The ratio t/l influences the lift coefficient in a
cascade. The cord length for a blade will therefore
increase when the radius becomes increase

15. Radial distribution of the
blade profile

16. Flow in the axial plane
The figure shows blades with two different design
of the blade in radial direction. This is because it
will influence the secondary flow in the radial
direction

17. Main dimension of a
Kaplan turbine

18. Diameter of the runner
o
Ω = ω ⋅ Qn
1 .0
C m l = 0 . 1 2 + 0 .1 8 0 Ω (tiln æ rm e t)
0 .5
m l
C
0
1 .5 2 .0 2 .5 3 .0
0
Ω
Qn =
Π⋅ D −d
⋅ c1m
( 2 2
)
4
⇓
Qn ⋅ 4
D=
Π ⋅ c1m

19. Height of the guide vanes
and runner diameter
P
0 .7
ns = n ⋅ 54
0 .6
H n
d /D
d /D , B 0/D
0 .5
B 0/D
0 .4
0 .3
300 400 500 600 700 800 900
ns

20. Gap between hub and ring
and the runner blades
Gap between the
blade and ring
Gap between the
blade and hub
0 .9 0
V Efficiencyd
s = x 1 0 -3 d
ir k n in g s g ra
0 .8 5
0 .8 0
0 1 2 3 4 5 6
S p a l t e å pGap x = 1 0 0 0 s / D
n in g

21. Runaway speed
2 .6
RRunaway/ nspeedu r t a l l
ϕ2 ϕ1
2 .4
u s n in g s ta ll o r m a lt
ϕ3
ϕ4
2 .2
ϕ5
ϕ6
2
V o it h
0 0 .5 1 .0 2 .0 3 .0
Cavitation scoefficient t σ
k a v ita jo n s k o e ff is ie n
10 − H S
σ=
H
The figure shows different runaway speed at
different runner blade openings. The runaway speed
is dependent of the cavitation as shown in the figure

22. Hill chart

23. Example
• Find the dimensions D, d and Bo
• Given data: P = 16,8 MW
H = 16 m
Qn = 120 m3/s
n = 125 rpm

24. Speed number:
2 ⋅ g ⋅ H = 2 ⋅ 9,82 ⋅16 = 17,7 m s
n ⋅ 2 ⋅ Π 125 ⋅ 2 ⋅ Π
ω= = = 13,1 rad
60 60 s
ω 13,1 rad
ω= = s = 0,74 m −1
2 ⋅ g ⋅ H 17,7 m
s
120 m3
Q s = 6,78 m 2
Qn = =
2 ⋅ g ⋅ H 17,7 m
s
o
Ω = ω ⋅ Q n = 0,74 ⋅ 6,78 = 1,93

25. Diameter, D:
c1m = 0,12 + 0,18 ⋅ o Ω = 0,467
Qn ⋅ 4 6,78 ⋅ 4
D= = = 4,3 m
Π ⋅ c1m Π ⋅ 0,467

26. Diameter, d:
P 22826 Hp
ns = n ⋅ = 125rpm ⋅ = 590
Hn 4
5
16m 54
0 .7
0 .6
d /D
d /D , B 0/D
0 .5
B 0/D
0 .4
0 .3
300 400 500 600 700 800 900
n s
d
= 0,45 ⇒ d = D ⋅ 0,45 = 1,9 m
D

27. Height, B:
0 .7
0 .6
d /D
d /D , B 0/D
0 .5
B 0/D
0 .4
0 .3
300 400 500 600 700 800 900
n s
BO
= 0,41 ⇒ BO = D ⋅ 0,41 = 1,76 m
D

28. Number of vanes, z:
l
= 0,95 Number of blades z
t
z=5