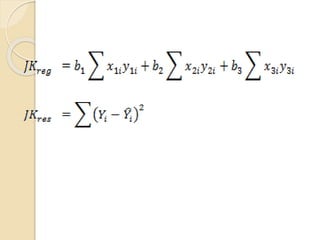Dokumen ini menjelaskan analisis regresi sebagai metode untuk mengukur pengaruh variabel independen terhadap variabel dependen, termasuk regresi linear sederhana dan berganda. Diberikan langkah-langkah dalam melakukan analisis regresi menggunakan SPSS, serta contoh aplikasi analisis terhadap data belajar siswa dan faktor-faktor yang mempengaruhi laju inflasi. Juga dibahas tentang pembentukan persamaan regresi dan uji keberartian regresi dalam konteks statistik.

1. REGRESI
Kelompok :
Denny Khairani
Desi Prawita
Maria Ulfa Handayani
Nurmala

2. DEFINISI
 Uji regresi digunakan untuk mengukur
pengaruh satu atau beberapa variabel
bebas terhadap variabel terikat.

3. Analisis regresi dapat dibedakan
menjadi dua, yaitu
 Analisis Regresi Linear Sederhana
adalah metode statistik yang berfungsi
untuk menguji sejauh mana hubungan
sebab akibat antara variabel
penyebab (X) terhadap variabel
akibatnya (Y).
 Analisis regresi linier berganda
ialah suatu alat analisis dalam ilmu
statistik yang berguna untuk
mengukur hubungan matematis
antara lebih dari 2 peubah.

4. Model Persamaan Regresi
Linear Sederhana adalah:
Y = a + bX
Dimana:
 Y = variabel response atau variabel
akibat (Dependent)
 X = variabel predictor atau variabel
faktor penyebab (Independent)
 a = konstanta
 b = koefisien regresi (kemiringan);
besaran response yang ditimbulkan
oleh predictor

5. Nilai- nilai a dan b dapat
dihitung:

6. Langkah- Langkah dalam
melakukan analisis regresi linear
sederhana:
 Menentukan tujuan dari melakukan analisis
regresi sederhana
 Mengidentifikasikan variabel faktor penyebab
(Predictor) dan variabel akibat (Response)
 Melakukan pengumpulan data
 Menghitung X2, Y2, XY dan total dari masing-
masing variabel tersebut
 Menghitung a dan b berdasarkan rumus
 Membuat model persamaan regresi linear
sederhana
 Melakukan prediksi atau peramalan terhadap
variabel faktor penyebab atau variabel akibat.

7. Bentuk umum persamaan
regresi linier berganda ialah :

8. Langkah- Langkah analisis regresi
ganda:
 Membuat H0 dan H1 dalam bentuk
kalimat
 Membuat H0 dan H1 dalam bentuk
statistik
 Membuat variabel bebas dan terikat
 Menentukan nilai konstanta dan
koefisien regresi
 Menginterpretasi koefisien regresi
 Melakukan uji keberartian regresi
 Melakukan perhitungan koefisien

9. Contoh Analisis Regresi
Linear Sederhana :
 Seorang guru fisika ingin mengetahui
apakah ada pengaruh lama belajar
dengan nilai ujian fisika siswa. Guru
tersebut mengambil data pada 20
orang siswa terhadap lama belajar
dan nilai ujian fisika seperti di bawah
ini:

10. Menghitung konstanta (a)

11. Menghitung konstanta (b)

12. Persamaan Regresi
Y = a + bX
Y = 21,58 +6,93X
 Kesimpulan : Konstanta sebesar 21,58
menyatakan jika jumlah lama belajar naik
(positif) maka nilai ujian fisika naik artinya
ada pengaruh jumlah jam belajar
terhadap nilai ujian fisika maka H1
diterima.

13. Langkah- Langkah Menggunakan
SPSS dalam Regresi Linear
Sederhana
 Langkah 1 :
SPSS Data Editor mempunyai 2 tipe
lingkungan kerja yaitu: Data View dan
Variable View. Untuk menyusun defenisi
variabel, posisi tampilan SPSS Data Editor
harus berada pilih ada ”Variabel View”.
Lakukan dengan mengklik tab sheet
Variable View yang berada dibagian kiri
bawah atau langsung menekan Ctrl+T.
Tampilan variable view juga dapat
dimunculkan dari View lalu pilih Variable

14.  Langkah 2 :
Pengisian Data
Aktifkan jendela data dengan mengklik Data
View
Ketikkan data yang sesuai dengan setiap
variabel yang telah di defenisikan pada
Variabel View
 Langkah 3:
Pengolahan Data dengan Persamaan
Regresi
Tampilkan lembar kerja dimana sudah
terdapatdata yang akan di analisis
Dari menu utama SPSS, klik menu Analyze,

15.  Setelah itu akan muncul kotak dialog
Linear Regression, pada kotak dialog ini
akan ditampilkan variabel-variabel yang
akan diuji. Masukkan variabel tak bebas Y
(variabel terikat) pada kotak Dependent
dan (variabel bebas ) pada kotak
Independent
 Klik kotak Statistics pada kotak dialog
Linear Regression, kemudian aktifkan
Estimate, Model fit, Descriptive dan
Casewise diagnostics, lalu klik Continue
untuk melanjutkan

16.  Kemudian klik tombol Options pada kotak
dialog Linear Regression sehingga muncul
kotak dialog yang baru. Pada Stepping
Method Criteria, aktifkan Use Probability
of F dengan standard error 0,05 oleh
karena itu masukkan nilai entry 0,05.
Aktifkan include constant inaquation
dan Exclude CasesLitwise pada Missing
Values

17.  Selanjutnya klik kotak Plots pada kotak
dialog Linear Regression untuk membuat
grafik. Isi kolom Y dengan pilihan
SDRESID dan kolom X dengan ZPRED,
kemudian klik Next. Isi lagi kolom Y
dengan ZPRED dan kolom X dengan
DEPENDNT. Pada Standardizes
Residual Plot, aktifkan Histogram dan
Normal Probability Plot. Lalu klik
Continue untuk melanjutkan
 Selanjutnya klik OK pada kotak dialog
Linear Regression

18. Contoh Analisis Regresi
Linear Berganda :
 Seorang mahasiswa ekonomi ingin
meneliti faktor-faktor apa saja yang
mempengaruhi laju inflasi di sumatera
utara dari tahun 2013 sampai tahun
2014 dengan data sebagai berikut

19. Dengan persamaan regresi:

20. Maka diperoleh persamaan
sebagai berikut:
Maka dari persamaan diatas dapat diperoleh dengan
cara metode crammer yaitu:

21. Dengan demikian diperoleh
persamaan regresi linier
berganda, yaitu:

22. Maka dari persamaan diatas
disimpulkan bahwa :
 Jika konstanta sebesar - 39,129
menyatakan jika laju inflasi turun
maka secara kontiniu suku bunga dan
jumlah uang beredar dan jika laju
inflasi turun maka kurs rupiah turun.
Oleh karena itu H1diterima berarti ada
pengaruh signifikan antara koefisien
laju inflasi dengan suku bunga, jumlah
uang beredar kurs rupiah dollar.

23. Uji Keberartian Regresi
 jika maka
ditolak
 jika maka
diterima

25.  Dari table distribusi Ftabel untuk dk
pembilang = 3, dk penyebut = n – k – 1 =
12 – 3 – 1 = 8
 sehingga didapat
maka ditolak dan diterima. Hal ini
berarti persamaan regresi linier berganda
atas Y, X1, X2, X3 dan bersifat nyata. Ini
berarti terdapat pengaruh yang signifikan
jumlah uang beredar,suku bunga bank,
dan kurs rupiah terhadap dollar secara
bersama-sama berpengaruhterhadap laju
inflasi.

26. Perhitungan Koefisien Determinasi
 Untuk koefisien korelasi ganda digunakan
rumus:
 menghitung Koefisien Determinasi (KD):

27. Langkah-langkah menggunakan
spss dalam regresi linier
berganda
 Langkah 1 :
Mengklik tab sheet Variable View yang
berada dibagian kiri bawah atau langsung
menekan Ctrl+T. Tampilan variable view
juga dapat dimunculkan dari View lalu
pilih Variable.
 Langkah 2 :
Pengisian Data
Klik Data View, Ketikkan data yang sesuai
dengan setiap variabel yang telah di
defenisikan pada Variabel View

28.  Langkah 3:
Pengolahan Data dengan Persamaan
Regresi
Tampilkan lembar kerja, dari menu utama
SPSS, klik menu Analyze, lalu pilih sub
menu Regression dan klik Linear.
Setelah itu akan muncul kotak dialog
Linear Regression. Masukkan variabel
tak bebas Y (variabel terikat) pada kotak
Dependentdan (variabel bebas ) pada
kotak Independent

29.  Klik kotak Statistics pada kotak dialog Linear
Regression, kemudian aktifkan Estimate,
Model fit, Descriptive dan Casewise
diagnostics, lalu klik Continue untuk
melanjutkan
 Selanjutnya klik kotak Plots pada kotak
dialog Linear Regression untuk membuat
grafik. Isi kolom Y dengan pilihan SDRESID
dan kolom X dengan ZPRED, kemudian klik
Next. Isi lagi kolom Y dengan ZPRED dan
kolom X dengan DEPENDNT. Pada
Standardizes Residual Plot, aktifkan
Histogram dan Normal Probability Plot.

30.  Kemudian klik tombol Options pada kotak
dialog Linear Regression sehingga muncul
kotak dialog yang baru. Pada Stepping
Method Criteria, aktifkan Use Probability
of F dengan standard error 0,05 oleh
karena itu masukkan nilai entry 0,05.
Aktifkan include constant inaquation
dan Exclude CasesLitwise pada Missing
Values
 Selanjutnya klik OK pada kotak dialog
Linear Regression