Download to read offline
![点推定
• 仮想的な母集団
i 名前
> p1 <- c(148, 160, 159, 153, 151, 140)
θi > p1
[1] 148 160 159 153 151 140
1 A 148 > mean(p1)
[1] 151.8333 母平均
2 B 160 > var(p1)
[1] 54.96667 母分散
3 C 159
4 D 153
5 E 151
6 F 140](https://image.slidesharecdn.com/k070-130416203041-phpapp01/85/K070-12-320.jpg)
![標本の取り出し方
6⋅5
M = N Cn = 6 C4 = = 15
2 ⋅1
標本 x1 x2 x3 x4 標本平均
1 ABCD 148 160 159 153 155.00
2 ABCE 148 160 159 151 154.50
3 ABCF 148 160 159 140 151.75 > mean(c(159, 153, 151, 140))
[1] 150.75
4 ABDE 148 160 153 151 153.00
途中省略
5 ABDF 148 160 153 140 150.25
6 ABEF 148 160 151 140 149.75 > mean(c(159, 153, 151, 140))
7 ACDE 148 159 153 151 152.75 [1] 150.75
> mean(c(155.00, 154.50, 151.75, 153.00, 150.25
8 ACDF 148 159 153 140 150.00
+ 149.75, 152.75, 150.00, 149.50, 148.00,
9 ACEF 148 159 151 140 149.50 + 155.75, 153.00, 152.50, 151.00, 150.75))
10 ADEF 148 153 151 140 148.00 [1] 151.8333
11 BCDE 160 159 153 151 155.75
12 BCDF 160 159 153 140 153.00
13 BCEF 160 159 151 140 152.75
14 BDEF 160 153 151 140 151.00
15 CDEF 159 153 151 140 150.75
総平均 151.833](https://image.slidesharecdn.com/k070-130416203041-phpapp01/85/K070-13-320.jpg)
More Related Content
K070 点推定
- 1. 統計的推測 Statistical Inference 推定と検定 母集団と標本 点推定 区間推定 2007.07.04 母平均のまとめ追加 2007.05.25 情報統計学 R より編集 2008.06.20 一部編集
- 2. 母集団と標本 • 母集団 population 調査したい全体 θ1θ2...θN 母集団の特性値 • 母平均 μ • 母分散 σ2 全数調査 • 時間がかかる • 費用がかかる • もともと不可能な場合
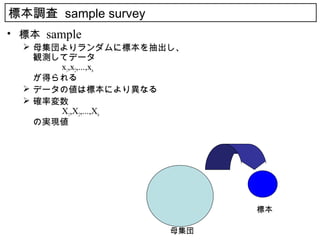
- 3. 標本調査 sample survey •標本 sample 母集団よりランダムに標本を抽出し、 観測してデータ x1,x2,...,xn が得られる データの値は標本により異なる 確率変数 X1,X2,...,Xn の実現値 標本 母集団
- 4. 可能な標本の組数 • 有限母集団の場合 母集団の構成要素（岡山大学の全学生数） N （ N=13,000 ） 標本数 ｎ （ ｎ＝１０ ） • 可能な標本の組数 M ＝ NCn • どの組を標本に選ぶか？！
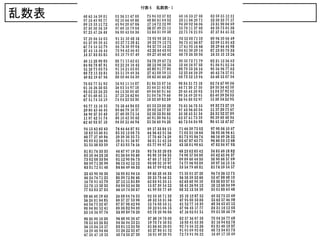
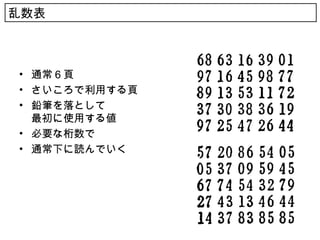
- 5. 無作為抽出 random sampling •独立性の保証 乱数 • 乱数表 • 乱数賽（サイコロ） • 非復元無作為抽出 without replacement • 復元無作為抽出 with replacement • 層別抽出法 stratified sampling
- 6.
- 7.
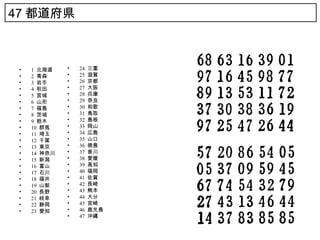
- 8. 乱数表 • 通常６頁 • さいころで利用する頁 •鉛筆を落として 最初に使用する値 • 必要な桁数で • 通常下に読んでいく
- 9. 47 都道府県 • 1 北海道 • 24 三重 • 2 青森 • 25 滋賀 • 3 岩手 • 26 京都 • 4 秋田 • 27 大阪 • 5 宮城 • 28 兵庫 • 6 山形 • 29 奈良 • 7 福島 • 30 和歌 • 8 茨城 • 31 鳥取 • 9 栃木 • 32 島根 • 10 群馬 • 33 岡山 • 11 埼玉 • 34 広島 • 12 千葉 • 35 山口 • 13 東京 • 36 徳島 • 14 神奈川 • 37 香川 • 15 新潟 • 38 愛媛 • 16 富山 • 39 高知 • 17 石川 • 40 福岡 • 18 福井 • 41 佐賀 • 19 山梨 • 42 長崎 • 20 長野 • 43 熊本 • 21 岐阜 • 44 大分 • 22 静岡 • 45 宮崎 • 23 愛知 • 46 鹿児島 • 47 沖縄
- 10. 層別無作為抽出法 • 市区町村、町丁字別、性別、学年別 のように、できるだけ均一な集団（層）に分け • 各層から無作為抽出 • 各層からどんな割合で標本をとるか 各層の大きさに比例して 各層のばらつきに比例して
- 11. 推定と検定 • 推定 estimation 母集団の特性値に何の情報もない 特性値の値はどんな値か知りたい • 点推定 point estimation • 区間推定 interval estimation/ confidence interval • 検定 testing 母集団の特性値についてある情報を持っている その情報が正しいか否かを知りたい • 帰無仮説と対立仮説 null hypothesis/ alternative hypothesis
- 12. 点推定 • 仮想的な母集団 i 名前 > p1 <- c(148, 160, 159, 153, 151, 140) θi > p1 [1] 148 160 159 153 151 140 1 A 148 > mean(p1) [1] 151.8333 母平均 2 B 160 > var(p1) [1] 54.96667 母分散 3 C 159 4 D 153 5 E 151 6 F 140
- 13. 標本の取り出し方 6⋅5 M = N Cn = 6 C4 = = 15 2 ⋅1 標本 x1 x2 x3 x4 標本平均 1 ABCD 148 160 159 153 155.00 2 ABCE 148 160 159 151 154.50 3 ABCF 148 160 159 140 151.75 > mean(c(159, 153, 151, 140)) [1] 150.75 4 ABDE 148 160 153 151 153.00 途中省略 5 ABDF 148 160 153 140 150.25 6 ABEF 148 160 151 140 149.75 > mean(c(159, 153, 151, 140)) 7 ACDE 148 159 153 151 152.75 [1] 150.75 > mean(c(155.00, 154.50, 151.75, 153.00, 150.25 8 ACDF 148 159 153 140 150.00 + 149.75, 152.75, 150.00, 149.50, 148.00, 9 ACEF 148 159 151 140 149.50 + 155.75, 153.00, 152.50, 151.00, 150.75)) 10 ADEF 148 153 151 140 148.00 [1] 151.8333 11 BCDE 160 159 153 151 155.75 12 BCDF 160 159 153 140 153.00 13 BCEF 160 159 151 140 152.75 14 BDEF 160 153 151 140 151.00 15 CDEF 159 153 151 140 150.75 総平均 151.833
- 14. 14 情報統計学 点推定
- 15. 点推定と区間推定 15 • 未知母数 ( パラメータ )θ を推定するには 2 つの方法がある 区間推定 • 区間で当てる 点推定 • 点で当てる たった一組のデータで求めた値が，母平均の値などに一致する可能性 は少ない • 区間推定 θ1≦θ≦θ2 のようにある幅をつけて母数 θ を推定する方法 • パラメータ θ が入るであろう範囲を一定の信頼度（確率）で指定 • 点推定 θ=θ0 として，幅をつけずに一個の推定値で推定 一点で当てる
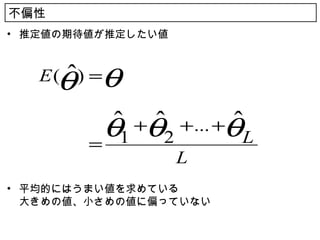
- 16. 点推定に望まれる性質 16 • 不偏性 標本に基づいて推定した値が，偏っていない • 何回も推定を繰り返すと，平均的には，推定したい値 θ にあって いる • 一致性 n を N に近づけたとき，全数調査の値，母集団のパラメータ θ に一致 してほしい • 有効性 一致性，不偏性を満たすものは多数 推定量の分散が小さいほうが望ましい • 最尤法 あとで説明。
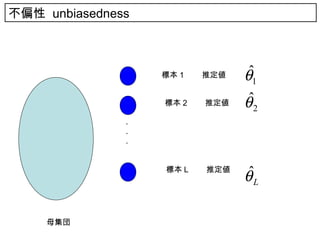
- 17. 不偏性 17 何回も推定を繰り返すと，平均的に は推定したい値 θ に合っている
- 18. 不偏性 unbiasedness 標本 1 推定値 ˆ θ1 標本 2 推定値 θˆ 2 . . . 標本 L 推定値 ˆ θL 母集団
- 19. 不偏性 • 推定値の期待値が推定したい値 θ θ E ( ˆ) = ˆ +θ +... +θ θ1 2 ˆ ˆ = L L • 平均的にはうまい値を求めている 大きめの値、小さめの値に偏っていない
- 20. 不偏性 20
- 21.
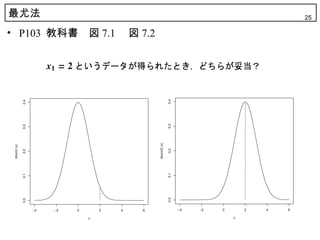
- 22. 一致性 22
- 23. 有効性 23
- 24.
- 25. 最尤法 25 • P103 教科書 図 7.1 図 7.2
- 26.
- 27.
- 28.
- 29. 正規分布の平均の点推定 29
- 30. 正規分布の母分散の点推定 30
- 31. 正規分布の平均の点推定 1 • 標本平均が 不偏性 µ ˆ = ∑ Xi n i 一致性 有効性 (BLUE) 最尤性 • のすべての意味で、一番良い推定量である。
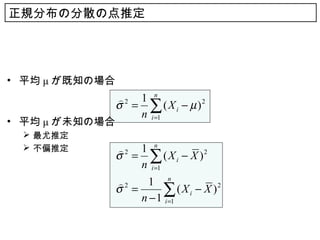
- 32. 正規分布の分散の点推定 • 平均 μが既知の場合 2 1 n σ = ∑ ( X i − µ )2 n i =1 • 平均 μ が未知の場合 最尤推定 不偏推定 2 1 n σ = ∑ ( X i − X )2 n i =1 2 1 n σ = ∑ n − 1 i =1 ( X i − X )2
- 33. レポート 33