1. 1 変数の集計
統計学入門
2008.04
2009.05.7 修正
2011.04.27 演習解答例追加
2012.04.25 演習 2 解答メモ追加
四分位偏差 説明追加
（講義後の修正まで）

2. データの分布
• だいたいどんな値 （代表値）
• 値のバラエティさ （ばらつき）
• その中でどんな値が多いか （ヒストグラ
ム） 2 0. 2
- 0. 0. 0
1 50 1 60 1 70 1 80 1 90
- 0. 0. 0 2
m
2 0.
• 分布形状 1 50 1 60
f 2
1 70 1 80 1 90
– 単峰性、双峰性、多峰性
– 左に偏った J 型分布、左右対称分布
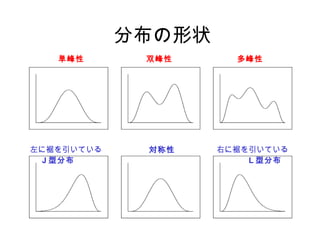
右に偏った L 型分布

3. 分布の形状
単峰性 双峰性 多峰性
左に裾を引いている 対称性 右に裾を引いている
J 型分布 L 型分布

4. 共通一次試験 (1980 年 )

5. 民間給与実態統計調査（平成 9
年）

6. データの縮約
• n 個のデータ
x1, x2, ・・・ xn
を数個の値にまとめる！
• 代表値（位置、 location ）
• ばらつき（広がり、 dispersion ）
• ５数要約
• グラフ表現

7. 代表値
• データが概ねどんな値か
• （数直線上の）どのあたりの位置にあ
- 0.0. 0 2
るか
2 0.
1 50 1 60 1 70 1 80 1 90
m
• （算術）平均値 arithmetic mean
• 中央値 median
• 最小値 minimum
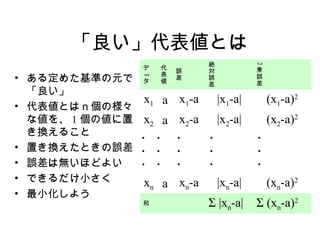
• 最大値 maximum

8. 「良い」代表値とは
絶
2
デ 代 乗
誤 対
表
• ある定めた基準の元で
ー
差 誤 誤
タ 値 差
差
「良い」
x1 a x1-a |x1-a| (x1-a)2
• 代表値とはｎ個の様々
な値を、 1 個の値に置 x2 a x2-a |x2-a| (x2-a)2
き換えること
・・ ・ ・ ・
• 置き換えたときの誤差
・・ ・ ・ ・
• 誤差は無いほどよい ・・ ・ ・ ・
• できるだけ小さく xn a xn-a |xn-a| (xn-a)2
• 最小化しよう
和 Σ |xn-a| Σ (xn-a)2

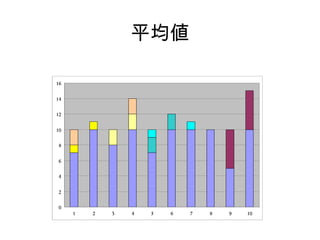
9. 平均値 (mean)
• mean x1 + x2 +  + xn
x=
n
• 代表値として一番良く使われる
• 最小 2 乗法 (Least Square Methods) の意味で最
良
誤差の 2 乗
Q(a)=(x1-a)2+(x2-a)2+ ・・・ +(xn-a)2
を最小にする a

10. 平均値
16
14
12
10
8
6
4
2
0
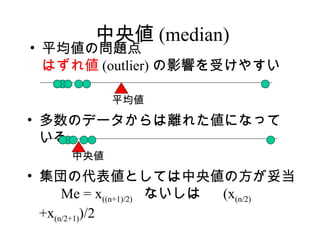
1 2 3 4 5 6 7 8 9 10

11. 中央値 (median)
• 平均値の問題点
はずれ値 (outlier) の影響を受けやすい
平均値
• 多数のデータからは離れた値になって
いる
中央値
• 集団の代表値としては中央値の方が妥当
Me = x((n+1)/2) ないしは (x(n/2)
+x(n/2+1))/2

12. 平均値と中央値との関係
• 平均値は外れ値の影響を受けやすい
• 中央値は外れ値に頑健 (robust)
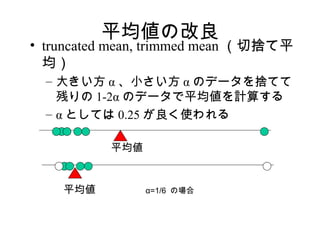
http://bstat.f7.ems.okayama-u.ac.jp/~yan/dataplot/

13. 平均値の改良
• truncated mean, trimmed mean （切捨て平
均）
– 大きい方 α 、小さい方 α のデータを捨てて
残りの 1-2α のデータで平均値を計算する
– α としては 0.25 が良く使われる
平均値
平均値 α=1/6 の場合

14. 最小値、最大値
• 洪水対策
過去のデータでの最大降水量に対
して対策を立てる
• 許容量
被害が起きた最小の値に対して対
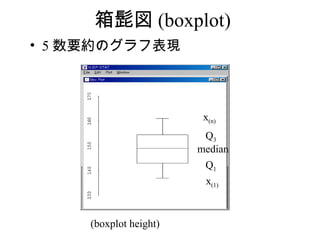
策を立てる

15. 5 数要約 (fivnum)
five-number summary
• 大きさの順序に並び換え
x(1)<x(2)< ・・・ <x(n)
• x(1) 最小値
• x(n/4) 第１四分位値 (Q1)
• x(2n/4) 第２四分位値 (Q2) ＝中央値
(Me)
• x(3n/4) 第３四分位値 (Q3)
• x(n) 最大値

16. 箱髭図 (boxplot)
• 5 数要約のグラフ表現
x(n)
Q3
median
Q1
x(1)
(boxplot height)

17. 度数分布表とヒストグラム
frequency table and histogram
• 階級数 k
– √n
– 1 + log n/log 2
– 10 ～ 20
• 階級の幅 w
– w=(x(n)-x(1))/k
• 端点 a0
a0 < x(1)< a0 + w/2

18. 度数分布表の追加情報
階級 階級値 度数 相対度数 累積度数 累積相対度数
a0~a1 m1 f1 f1/n f1 (f1)/n
a1~a2 m2 f2 f2/n f1+f2 (f1+f2)/n
ak-1~ak mk fk fk/n f1+‥+fk (f1+‥+fk)/n
n 1

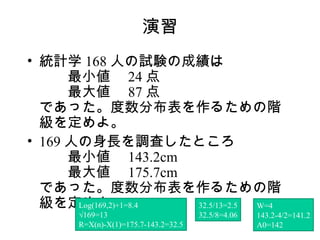
19. 演習
• 統計学 168 人の試験の成績は
最小値 24 点
最大値 87 点
であった。度数分布表を作るための階
級を定めよ。
• 169 人の身長を調査したところ
最小値 143.2cm
最大値 175.7cm
であった。度数分布表を作るための階
級を定めよ。

20. 演習問題の解答例
n=168 人 階級
x(1)= 最小値 =24 22～27
x(n)= 最大値 =87 27～32
n = 168 = 12.96 32～37
log 168 2.2253 37～42
1 + log 2 n = 1 + = 1+ = 8.393
log 2 0.3010 42～47
階級数k = 8～13 47～52
x( n ) − x(1) 87 − 24 52～57
63
幅 w = = = 4.85～ = 7.85 57～62
k 13 8
w = 5 と決める 62～67
67～72
端点 a0 : a0 ≤ x(1) ≤ a0 + w / 2
72～77
a0 ≤ 24 ≤ a0 + 5 / 2
77～82
a0 ≤ 24 ≤ a0 + 2.5
82～87
24 − 2.5 = 21.5 ≤ a0 ≤ 24 87～92
a0 = 22 と決める

21. 講 評
「階級を定める」ということは、
すべての小区間を決めること！ 22～27 22.5～27.5
27～32 27.5～32.5
階級数 ｋ、 32.5～37.5
32～37
階級の幅 ｗ、 37.5～42.5
37～42
端点 a0 を決めるだけでは不十分。 42.5～47.5
42～47
47～52 47.5～52.5
端点の値がどちらの階級に属するか（以下、未 52.5～57.5
52～57
満）という議論を避けるために、端点の値がデ 57.5～62.5
57～62
ータに出てこないように端点を定めることもあ
62～67 62.5～67.5
る。
67～72 67.5～72.5
72～77 72.5～77.5
データの有効桁（成績のよう整数値のデータで
あれば、１の位）に対して、その一つ下の桁（ 77～82 77.5～82.5
整数値であれば、小数点以下１桁目）に５を付 82～87 82.5～87.5
けた値を端点の値とする。 87～92 87.5～92.5
前の演習問題であれば、右側のように定めれば
良い。

22. 演習
• 統計学 168 人の試験の成績は
最小値 24 点
最大値 87 点
であった。度数分布表を作るための階
級を定めよ。
• 169 人の身長を調査したところ
最小値 143.2cm
最大値 175.7cm
であった。度数分布表を作るための階
級を定めよ。
Log(169,2)+1=8.4 32.5/13=2.5 W=4
√169=13 32.5/8=4.06 143.2-4/2=141.2
R=X(n)-X(1)=175.7-143.2=32.5 A0=142

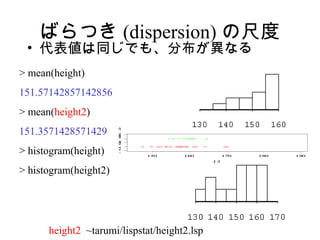
23. ばらつき (dispersion) の尺度
• 代表値は同じでも、分布が異なる
> mean(height)
151.57142857142856
> mean(height2)
151.3571428571429
2 0. 2
- 0. 0. 0
> histogram(height) 1 50 1 60 1 70 1 80 1 90
f 2
> histogram(height2)
height2 ~tarumi/lispstat/height2.lsp

24. バラツキの尺度
• 範囲 (range)
• 四分位範囲 (interquartile range)
• 平均偏差 (mean deviation)
• 分散 (variance)
• 標準偏差 (standard deviation)

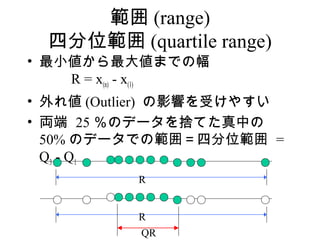
25. 範囲 (range)
四分位範囲 (quartile range)
• 最小値から最大値までの幅
R = x(n) - x(1)
• 外れ値 (Outlier) の影響を受けやすい
• 両端 25 ％のデータを捨てた真中の
50% のデータでの範囲＝四分位範囲 =
Q3 - Q1
R
R
QR

26. 四分位偏差
• 平成 24 年度からの高校数学Ⅰでは四分位
範囲の代わりに、四分位偏差が取り上
げられている。
Q3 − Q1 四分位範囲
四分位偏差 = =
2 2
• 統計学の分野では四分位範囲の方がよ
くつかわれる。

27. 平均偏差 (mean deviation)
• 偏差
d i = xi − x
• 平均偏差
n n
1 1 
d = d = ∑ | di | = ∑ |x i − x |
n i =1 n i =1

28. 分散 (variance)
標準偏差 (standard deviation)
• 分散 偏差２乗の平均
1 n
s = ∑ ( xi − x )
2 2
n i =1
n
1
= (∑ xi ) − ( x )
2 2
n i =1
• 標準偏差 分散の平方根
1 n
s= s =
2
∑ ( xi − x )
n i =1
2

29. 不偏分散 (unbiased variance)
• 標本分散としては不偏分散 u2 を使うこ
とも多い
1 n
s = ∑ ( xi − x )
2 2
n i =1
n
1
u =
2
∑ ( xi − x )
n − 1 i =1
2
2
ns
=
n −1

30. 演習
• height
– 148, 160, 159, 153, 151, 140, 156, 137, 149, 160, 151,
157, 157, 144
– 和 2122 2 乗和 322338
• height2
– 138, 162, 158, 151, 145, 134, 160, 137, 151, 163, 152,
163, 158, 147
– 和 2119 2 乗和 322019
• weight
– 41, 49, 45, 43, 42, 29, 49, 31, 47, 47, 42, 39, 48, 36
– 和 588 2 乗和 25226