1. 1
情報統計学
確率分布
独立性
期待値と分散
正規分布
20120525 一部修正

2. 確率 2
• A という結果が起きる確率→ Pr(A) と書く。

3. 確率分布 3
• 確率分布
その結果がどんな確率で起きるかをまとめたもの
 離散型分布
 連続型分布
• 特定の値 a を取る確率は 0
• 幅をつけて考える

4. 累積分布関数 Cummulative Distribution Function, CDF 4
• 定義
 確率変数 X に対して
を確率変数 X の累積分布関数という。
• 確率密度関数
 累積分布関数 F(x) が微分可能なとき，導関数
を確率変数 X の（確率）密度関数 (probability density function, pdf) とい
う。
確率密度関数があるときには，

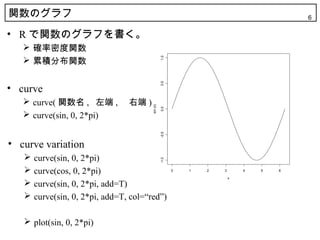
5. 分布関数の性質 5

6. 関数のグラフ 6
• R で関数のグラフを書く。
 確率密度関数
 累積分布関数
1.0
0.5
• curve
 curve( 関数名 , 左端 , 右端 )
sin (x)
0.0
 curve(sin, 0, 2*pi)
-0.5
• curve variation
 curve(sin, 0, 2*pi) -1.0
 curve(cos, 0, 2*pi) 0 1 2 3 4 5 6
x
 curve(sin, 0, 2*pi, add=T)
 curve(sin, 0, 2*pi, add=T, col=“red”)
 plot(sin, 0, 2*pi)

7. 関数を探す 7
• 正規分布 (normal distribution)
• 関数名に Normal が付くものを探す
 help.search(“Normal”)
• Normal の中に関連するものがありそう
 help(“Normal”)
で使い方をみる
または
 ?Normal
でもよい。

8. 分布に関連する関数 8
• 分布名 • 関数名の頭文字
 正規分布 norm  p分布名 分布関数
 ｔ - 分布 t  Pr(X<x)
 カイ 2 乗分布 chisq  d 分布名 密
 F分布 f 度関数
 一様分布  density function
unif
 二項分布  q 分布名 分
binom
位点
 ポアソン分 poi
 quantile
 r 分布名 乱
数
 random number

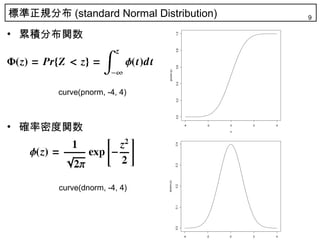
9. 標準正規分布 (standard Normal Distribution) 9
• 累積分布関数
1.0
0.8
0.6
pnorm (x)
0.4
curve(pnorm, -4, 4)
0.2
0.0
• 確率密度関数 -4 -2 0
x
2 4
0.4
0.3
dnorm (x)
curve(dnorm, -4, 4)
0.2
0.1
0.0
-4 -2 0 2 4

10. 正規分布表の使い方
• 数表は「標準正規分布」 Z ～ N(0,1)
Pr(Z<0.91)

11. 11
下側 α 点
qnorm 関数
qnorm(0.025, lower.tail = F)
qnorm(0.025)

12. 標準化、偏差値 12
• 標準化
X −µ
X ~ N (µ ,σ ) ⇒ Z =
2
~ N (0,1)
σ
• 偏差値
X ~ N (µ ,σ )
2
X −µ
⇒ 偏差値 = ×10 + 50 ~ N (50,10 )
2
σ

13. 演習
• Z ～ N(0,1) 、 X ～ N(158,25) のとき次の確
率を求めよ。
1) Pr(0 ≤ Z < 1)
2) Pr(1 ≤ Z )
3) Pr(−2 ≤ Z < −1)
4) Pr( Z ≥ k ) = 0.05 となるkの値
5) Pr(| Z |< 1)
6) Pr(| Z |> 2)
7) Pr(150 ≤ X < 160)
8) Pr(| X − 158 |> k ) = 0.05 となるkの値

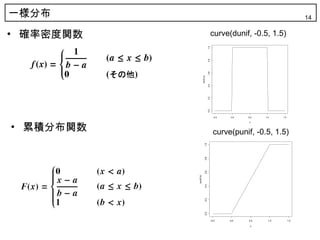
14. 一様分布 14
• 確率密度関数 curve(dunif, -0.5, 1.5)
1.0
0.8
0.6
dunif (x)
0.4
0.2
0.0
-0.5 0.0 0.5 1.0 1.5
• 累積分布関数
x
curve(punif, -0.5, 1.5)
1.0
0.8
0.6
punif (x)
0.4
0.2
0.0
-0.5 0.0 0.5 1.0 1.5
x

15. 二項分布 (Binomial distribution)
• 1 回の試行 ( 実験 ) で A という事象が起きるか、
起
きないか
• A という事象が起きる確率が p 、
起きない確率が q=1-p
• この試行をｎ回行ったとき、 A が起きる回数を
X とする。
• X の分布を二項分布といい、
X ～ Bi(n, p)
と表す。

16. 二項分布 その２
• X の取り得る値 ｎ回中の回数なので
0, 1, 2, …, n
• Pr(X=k) = A がｎ回中ｋ回起きる確率
= nCk pk(1-p)n-k
• 分布関数
[ x]
F ( x) = Pr( X ≤ x) = ∑ pk
k =0
[ x]
∑ n C x p k (1 − p ) n − k
=
k =0

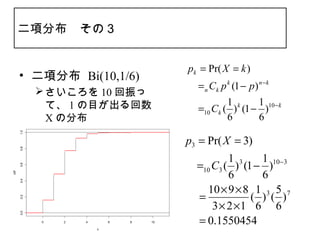
17. 二項分布 その３
pk = Pr( X = k )
• 二項分布 Bi(10,1/6)
Ck p k (1 − p ) n − k
=n
 さいころを 10 回振っ
て、 1 の目が出る回数 1 1
Ck ( ) k (1 − )10− k
=10
X の分布 6 6
1.0
p3 = Pr( X = 3)
0.8
1 3 1 10−3
C3 ( ) (1 − )
=10
0.6
6 6
cdf
0.4
10 × 9 × 8 1 3 5 7
= ( ) ( )
0.2
3 × 2 ×1 6 6
0.0
0 2 4 6 8 10 0.1550454
=
x

18. 二項分布 Bi(10,1/6) の分布関数
階段関数 (step function)
1.0
0.8
pbinom(xx, 10, 1/6)
0.6
0.4
0.2
0.0
0 2 4 6 8 10
xx
> pbinom(x,10,1/6)
[1] 0.1615056 0.4845167 0.7752268 0.9302722 0.9845380 0.9975618 0.9997325
[8] 0.9999806 0.9999992 1.0000000 1.0000000

19. シミュレーション （数値実験） simulation 19
 複雑な問題で式を求めるのが難しい
 費用がかかりすぎる・時間がかかりすぎる
• シミュレーションとは
 乱数を使って理論的な結果を検証
 理論的には結果を得ることが難しい内容を求めること
• 乱数
 R では
• 乱数は，分布名に r をつけたもの
• 例：一様乱数 runif
• 正規乱数 rnorm

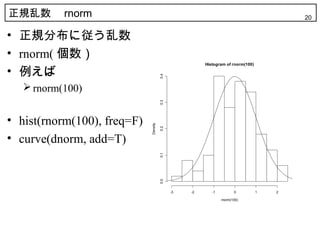
20. 正規乱数 rnorm 20
• 正規分布に従う乱数
• rnorm( 個数）
Histogram of rnorm(100)
• 例えば
0.4
 rnorm(100)
0.3
• hist(rnorm(100), freq=F)
Density
0.2
• curve(dnorm, add=T)
0.1
0.0
-3 -2 -1 0 1 2
rnorm(100)

21. 円周率のシミュレーション 21
• 一辺の長さ 1 の正方形
 面積 1 • 区間 [0, 1] の一様乱数を 2 個
• 半径 1 の 1/4 円  それを x 座標， y 座標とする点 P (x, y) を考え
 面積 π/4 る
• その点は正方形の中
• さらに 1/4 円の中に落ちる比率は１： π/4
1.0
0.8
そういう点を n 個発生させ
る
0.6
circ (x)
• 1/4 円内の点の個数を m 0.4
• 全体の点の個数を n
m/n ≒ π/4
0.2
0.0
0.0 0.2 0.4 0.6 0.8 1.0
x

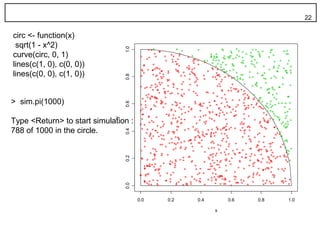
22. 22
circ <- function(x)
sqrt(1 - x^2)
1.0
curve(circ, 0, 1)
lines(c(1, 0), c(0, 0))
lines(c(0, 0), c(1, 0))
0.8
> sim.pi(1000)
0.6
Type <Return> to start simulation :
y
788 of 1000 in the circle. 0.4
0.2
0.0
0.0 0.2 0.4 0.6 0.8 1.0
x

23. 条件付確率 (conditional prob.)
• 事象 A が起きたという条件の下で
事象 B が起きる確率を考える
• 例 女性で身長が１７０ｃｍ以上
B
Pr( A ∩ B )
Pr( B | A) =
Pr( A) A
Pr(身長 ≥ 170.0 かつ 女性)
Pr(身長 ≥ 170.0 | 女性) =
Pr(女性)
0.03976
= = 0.0082
0.485

24. 独立事象
• 条件付確率が条件に無関係のとき
2 つの事象は独立という
Pr( B | A) = Pr( B )
Pr( A ∩ B )
Pr( B | A) = = Pr( B )
Pr( A)
Pr( A ∩ B ) = Pr( A) Pr( B )

25. 条件付分布
• X=x という条件の下での Y の分布
G ( y | x) = Pr(Y < y | X = x)
Pr(Y < y and X = x)
=
Pr( X = x)
h ( x, y )
g ( y | x) =
f ( x)
h( x, y ) = f ( x ) g ( y | x )
g ( y ) f ( x | y )
=

26. 独立性
• 2 つの確率変数 X, Y が独立
 分布関数
H ( x, y ) = Pr( X < x, Y < y )
Pr( X < x) Pr(Y < y )
=
F ( x)G ( y )
=
 密度関数
h ( x, y ) = f ( x ) g ( y )

27. 期待値 (Expectation)
• データの平均（代表値、どんな値）
data : x1 , x2 , , xn
x1 + x2 +  + xn
mean : x =
n
• 確率変数（分布）の期待値（どんな値）
取り得る値 : a1 , a2 , , ak
各値の確率 : p1 , p2 , , pk
平均 : E ( X ) = a1 p1 + a2 p2 +  + ak pk

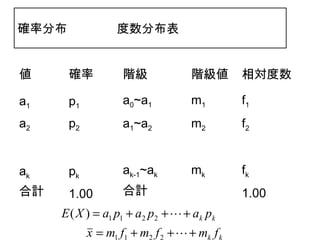
28. 確率分布 度数分布表
値 確率 階級 階級値 相対度数
a1 p1 a0~a1 m1 f1
a2 p2 a1~a2 m2 f2
ak pk ak-1~ak mk fk
合計 1.00 合計 1.00
E ( X ) = a1 p1 + a2 p2 +  + ak pk
x = m1 f1 + m2 f 2 +  + mk f k

29. 期待値と分散
X 確率変数
f ( x) Xの密度関数
離散型の場合は
Xの期待値(平均) 積分の代わりに
∞ 和 (Σ) を使う
E ( X ) = ∫ x f ( x)dx
−∞
∞
E (φ ( X )) = ∫ φ ( x) f ( x)dx
−∞
Xの分散
V ( X ) = E ( X − E ( X )) 2 φ ( x) = {x − E ( X )}2
∞
∫ {x − E ( X )}2 f ( x)dx
=
−∞
E ( X 2 ) − {E ( X )}2
=

30. 主な分布の期待と分散
X ~ Bi (n, p )
E ( X ) = np, V ( X ) = npq
X ~ Po(λ )
E ( X ) = λ , V ( X ) = λ
X ~ U ( a, b)
E ( X ) = (a + b) / 2, V ( X ) = (b − a ) / 12
2
X ~ N (µ ,σ ) 2
E ( X ) = µ , V ( X ) = σ 2

31. 31
情報統計学
χ2 分布
t 分布
F 分布

32. 標本分布 32
• 正規分布から導かれる分布
χ2 分布
t 分布
F 分布

33. χ2 分布 33
• 自由度 m の χ2 分布
 確率密度関数
•E(Y)=m
•Var(Y)=2m

34. χ2 分布 34
• 確率変数 Z が標準正規分布 N(0,12) に従っているとき，
Y = Z2
の分布は自由度 1 の χ2 分布に従う。
• 確率変数 X1, X2, …, Xn が互いに独立で， Xi が正規分布 N(0,12)
に従うとき，
Z = X12 + X22 + … + Xn2
は自由度 n の χ2 分布に従う。

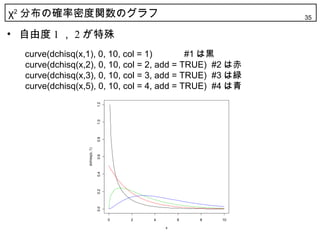
35. χ2 分布の確率密度関数のグラフ 35
• 自由度 1 ， 2 が特殊
curve(dchisq(x,1), 0, 10, col = 1) #1 は黒
curve(dchisq(x,2), 0, 10, col = 2, add = TRUE) #2 は赤
curve(dchisq(x,3), 0, 10, col = 3, add = TRUE) #3 は緑
curve(dchisq(x,5), 0, 10, col = 4, add = TRUE) #4 は青
1.2
1.0
0.8
dchisq(x, 1)
0.6
0.4
0.2
0.0
0 2 4 6 8 10
x

36. シミュレーションによる導出 36
• 標準正規分布を２乗すると χ2 分布になることを乱数を使って確かめる
1. 正規乱数 z を 1 つ取る
2. y=z2 を計算する
3. これを n 回繰り返し， y の値を n 個とる
4. Y の分布を図示し，理論的なものと比較する
Histogram of nrdata
> nrdata <- rnorm(1000)
> summary(nrdata)
200
Min. 1st Qu. Median Mean 3rd Qu. Max.
-3.34300 -0.66630 0.11250 0.05922 0.75260 3.16000
> sd(nrdata)
150
[1] 1.025253
Frequency
> hist(nrdata)
100
50
0
-3 -2 -1 0 1 2 3
nrdata

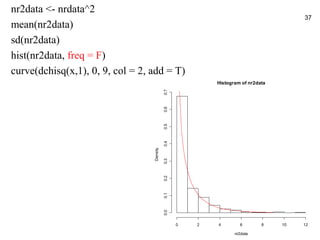
37. nr2data <- nrdata^2
37
mean(nr2data)
sd(nr2data)
hist(nr2data, freq = F)
curve(dchisq(x,1), 0, 9, col = 2, add = T)
Histogram of nr2data
0.7
0.6
0.5
0.4
Density
0.3
0.2
0.1
0.0
0 2 4 6 8 10 12
nr2data

38. レポート 38
1. X が自由度 m の χ2 分布に従い， Y が自由度 n の χ2 分布に従っ
て，互いに独立であれば
Z=X+Y
の分布は，自由度 (m+n) の χ2 分布に従う。
再生性というが，このことをシミュレーションを使って確認
せよ。
2. 正規分布も再生性を持つ。このことをシミュレーションを用
いて確かめよ。

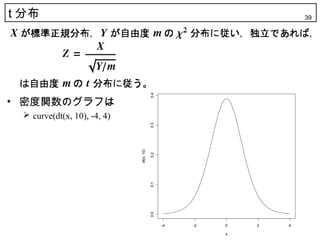
39. t 分布 39
0.4
• 密度関数のグラフは
 curve(dt(x, 10), -4, 4)
0.3
dt(x, 10)
0.2
0.1
0.0
-4 -2 0 2 4
x

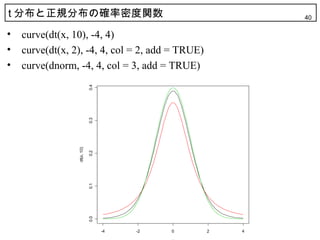
40. t 分布と正規分布の確率密度関数 40
• curve(dt(x, 10), -4, 4)
• curve(dt(x, 2), -4, 4, col = 2, add = TRUE)
• curve(dnorm, -4, 4, col = 3, add = TRUE)
0.4
0.3
dt(x, 10)
0.2
0.1
0.0
-4 -2 0 2 4

41. t 分布のパーセント点 41
> qt(0.05, 5)
> qt(0.05, c(1, 2, 3, 4, 5, 10, 20, 50, 100))
[1] -6.313752 -2.919986 -2.353363 -2.131847 -2.015048 -1.812461
-1.724718
[8] -1.675905 -1.660234
> qt(c(0.05, 0.95), 5)
[1] -2.015048 2.015048
> pt(2.015048, 5)
[1] 0.95

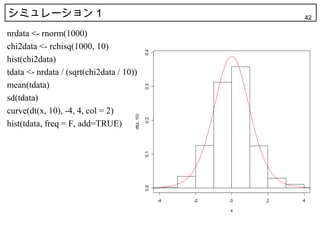
42. シミュレーション 1 42
nrdata <- rnorm(1000)
chi2data <- rchisq(1000, 10)
0.4
hist(chi2data)
tdata <- nrdata / (sqrt(chi2data / 10))
mean(tdata)
0.3
sd(tdata)
curve(dt(x, 10), -4, 4, col = 2)
dt(x, 10)
0.2
hist(tdata, freq = F, add=TRUE)
0.1
0.0
-4 -2 0 2 4
x

43. シミュレーション 2 43

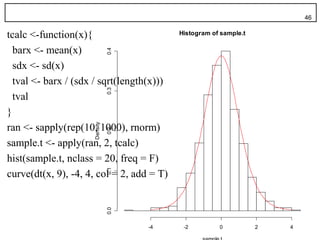
44. 44

45. 45

46. 46
tcalc <-function(x){ Histogram of sample.t
barx <- mean(x)
0.4
sdx <- sd(x)
tval <- barx / (sdx / sqrt(length(x)))
0.3
tval
}
ran <- sapply(rep(10, 1000), rnorm)
Density
0.2
sample.t <- apply(ran, 2, tcalc)
hist(sample.t, nclass = 20, freq = F)
0.1
curve(dt(x, 9), -4, 4, col = 2, add = T)
0.0
-4 -2 0 2 4

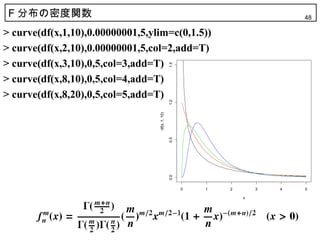
47. F 分布 47

48. F 分布の密度関数 48
> curve(df(x,1,10),0.00000001,5,ylim=c(0,1.5))
> curve(df(x,2,10),0.00000001,5,col=2,add=T)
> curve(df(x,3,10),0,5,col=3,add=T)
1.5
> curve(df(x,8,10),0,5,col=4,add=T)
> curve(df(x,8,20),0,5,col=5,add=T)
1.0
df(x, 1, 10)
0.5
0.0
0 1 2 3 4 5
x

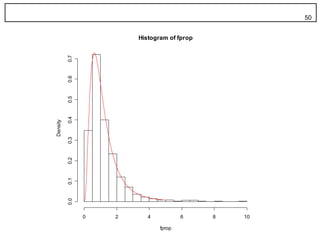
49. シミュレーション 49
> c8rand <- rchisq(1000, 8)
> c10rand <- rchisq(1000, 10)
> fprop <- (c8rand / 8) / (c10rand / 10)
> hist(fprop, nclass = 20, freq = F)
> hist(fprop, nclass = 20, freq = F)$count
> curve(df(x,8,10), 0, 5, col = 2, add = TRUE)

50. 50
Histogram of fprop
0.7
0.6
0.5
0.4
Density
0.3
0.2
0.1
0.0
0 2 4 6 8 10
fprop