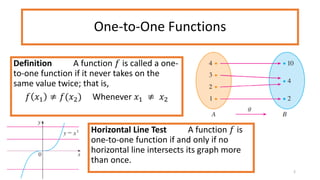
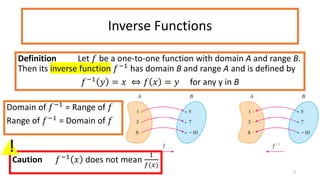
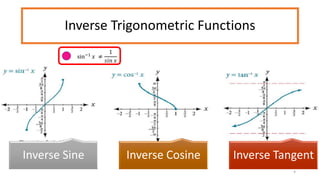
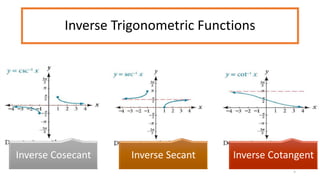
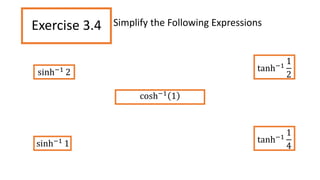
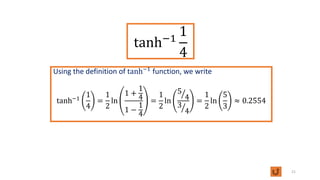
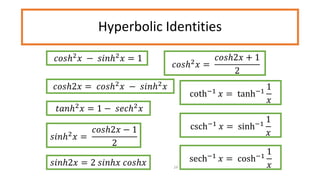
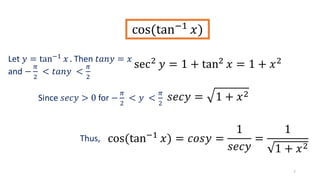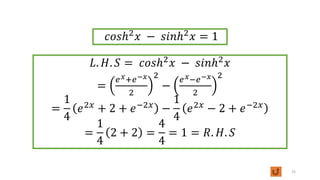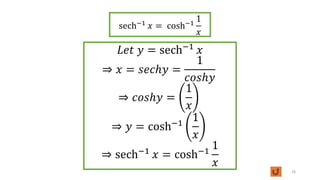This document discusses inverse functions. It begins by defining one-to-one functions and inverse functions. A function f is one-to-one if it passes the horizontal line test. The inverse function f^-1 has the domain and range swapped and satisfies the equation f(x) = y if and only if f^-1(y) = x. Examples are provided of finding inverse trigonometric, hyperbolic, and other functions. The document concludes with exercises involving evaluating functions, finding inverse functions, and using function composition to determine if functions are inverses.

1. Inverse Functions
Chapter 3
This Photo by Unknown Author is licensed under CC BY

2. One-to-One Functions
Definition A function 𝑓 is called a one-
to-one function if it never takes on the
same value twice; that is,
𝑓 𝑥1 ≠ 𝑓(𝑥2) Whenever 𝑥1 ≠ 𝑥2
2
Horizontal Line Test A function 𝑓 is
one-to-one function if and only if no
horizontal line intersects its graph more
than once.

3. Inverse Functions
3
Definition Let 𝑓 be a one-to-one function with domain A and range B.
Then its inverse function 𝑓−1 has domain B and range A and is defined by
𝑓−1
𝑦 = 𝑥 ⇔ 𝑓 𝑥 = 𝑦 for any y in B
Domain of 𝑓−1
= Range of 𝑓
Range of 𝑓−1
= Domain of 𝑓
Caution 𝑓−1 𝑥 does not mean
1
𝑓(𝑥)
!

4. Inverse Trigonometric Functions
Inverse Sine Inverse Cosine Inverse Tangent
4
sin−1 𝑥 ≠
1
𝑠𝑖𝑛 𝑥

5. Inverse Trigonometric Functions
Inverse Cosecant Inverse Secant Inverse Cotangent
5

6. Example 3.1
6
Simplify the following expressions
sin(tan−1
𝑥2 − 2𝑥)) , 𝑥 ≥ 2
csc(arctan 2𝑥 )
tan(sin−1
𝑥)
sin(tan−1
𝑥)
cos(tan−1
𝑥)

7. 7
cos(tan−1
𝑥)
sec2
𝑦 = 1 + tan2
𝑥 = 1 + 𝑥2
𝑠𝑒𝑐𝑦 = 1 + 𝑥2
cos(tan−1
𝑥) = 𝑐𝑜𝑠𝑦 =
1
𝑠𝑒𝑐𝑦
=
1
1 + 𝑥2
Let 𝑦 = tan−1 𝑥 . Then 𝑡𝑎𝑛𝑦 = 𝑥
and −
𝜋
2
< 𝑡𝑎𝑛𝑦 <
𝜋
2
Since 𝑠𝑒𝑐𝑦 > 0 for −
𝜋
2
< 𝑦 <
𝜋
2
Thus,

8. 8
cos(tan−1
𝑥)
cos(tan−1
𝑥) = 𝑐𝑜𝑠𝑦 =
1
1 + 𝑥2
Instead of using trigonometric identities as in
Solution 1, it is perhaps easier to use a diagram.
If 𝑦 = tan−1 𝑥, then 𝑡𝑎𝑛𝑦 = 𝑥, and we can read
from the diagram

9. 9
csc(arctan 2𝑥 )
Let 𝜃 = arctan 2𝑥
⇒∴ 𝑡𝑎𝑛𝜃 = 2𝑥
∴ csc arctan 2𝑥 = 𝑐𝑠𝑐𝜃 =
4𝑥2 + 1
2𝑥

10. 10
sin(tan−1
𝑥2 − 2𝑥)) , 𝑥 ≥ 2
Let 𝜃 = tan−1
𝑥2 − 2𝑥 , 𝑥 ≥ 2
⇒∴ 𝑡𝑎𝑛𝜃 = 𝑥2 − 2𝑥
∴ sin(tan−1
𝑥2 − 2𝑥)) = 𝑠𝑖𝑛𝜃 =
𝑥2 − 2𝑥
𝑥 − 1
, 𝑥 ≥ 2

11. 11
tan(sin−1
𝑥)
Let 𝜃 = sin−1
𝑥
⇒∴ 𝑠𝑖𝑛𝜃 = 𝑥
∴ tan(sin−1
𝑥) = 𝑡𝑎𝑛𝜃 =
𝑥
1 − 𝑥2

12. 12
sin(tan−1
𝑥)
Let 𝜃 = tan−1
𝑥
⇒∴ 𝑡𝑎𝑛𝜃 = 𝑥
∴ sin(tan−1
𝑥) = 𝑠𝑖𝑛𝜃 =
𝑥
𝑥2 + 1

13. How to find the inverse function of a one-to-one
function 𝑓
13
Step 1
Step 2
Step 3
Write 𝑦 = 𝑓(𝑥)
Solve this equation for x in terms of y (if possible).
To express 𝑓−1 𝑥 as a function of x, interchange x and y. The resulting
equation is 𝑦 = 𝑓−1 𝑥 .

14. Example 3.2
14
Find the Inverse Function of 𝑓 𝑥 =
𝑥3
+ 2
𝑦 = 𝑥3
+ 2
𝑥3
= 𝑦 − 2
𝑥 = 3
𝑦 − 2
𝑦 =
3
𝑥 − 2
𝑓−1
𝑥 =
3
𝑥 − 2
Then we solve this equation for x:
Finally, we interchange and :
Therefore, the inverse function is

15. Example 3.3
15
Find the Inverse Function of 𝑓 𝑥 =
1+𝑒𝑥
1−𝑒𝑥
𝑥 = 𝑙𝑛
𝑦 − 1
𝑦 + 1
solve for x
Exchange y by x.
Apply ln
𝑦 =
1 + 𝑒𝑥
1 − 𝑒𝑥
𝑦 − 𝑦𝑒𝑥
= 1 + 𝑒𝑥
𝑦𝑒𝑥
+ 𝑒𝑥
= 𝑦 − 1
𝑒𝑥
=
𝑦 − 1
𝑦 + 1
𝑓−1
𝑥 = 𝑙𝑛
𝑥 − 1
𝑥 + 1

16. Inverse Hyperbolic Functions
Inverse
Hyperbolic
Sine of x
sinh−1
𝑥 = ln 𝑥 + 𝑥2 + 1
Inverse
Hyperbolic
Cosine of x
𝑐𝑜𝑠ℎ−1 𝑥 = ln 𝑥 + 𝑥2 − 1
Inverse
Hyperbolic of
Tangent of x
tanh−1
𝑥 =
1
2
ln
1 + 𝑥
1 − 𝑥
16

17. Exercise 3.4
cosh−1 1
Simplify the Following Expressions
tanh−1
1
4
sinh−1 2
sinh−1 1
tanh−1
1
2

18. sinh−1
2
Using the definition of sinh−1 function, we write
sinh−1
2 = ln 2 + 22 + 1 = ln(2 + 5) ≈ 1.4436
18

19. cosh−1
1
Using the definition of cosh−1 function, we write
𝑐𝑜𝑠ℎ−1
1 = ln 1 + 12 − 1 = ln 1 + 0 = 𝑙𝑛1
19

20. sinh−1
1
Using the definition of sinh−1 function, we write
sinh−1
1 = ln 1 + 12 + 1 = ln(1 + 2)
20

21. tanh−1
1
4
Using the definition of tanh−1 function, we write
tanh−1
1
4
=
1
2
ln
1 +
1
4
1 −
1
4
=
1
2
ln
ൗ
5
4
ൗ
3
4
=
1
2
ln
5
3
≈ 0.2554
21

22. tanh−1
1
2
Using the definition of tanh−1 function, we write
tanh−1
1
2
=
1
2
ln
1 +
1
2
1 −
1
2
=
1
2
ln
1.5
0.5
=
1
2
ln 3
22

23. Inverse Hyperbolic Functions
Inverse
Hyperbolic
Cosecant of x
csch−1 𝑥 = ln
1
𝑥
+
1 + 𝑥2
𝑥
Inverse
Hyperbolic
Secant of x
𝑠𝑒𝑐ℎ−1
𝑥 = ln
1 + 1 − 𝑥2
𝑥
Inverse
Hyperbolic of
Cotangent of x
coth−1𝑥 =
1
2
ln
𝑥 + 1
𝑥 − 1
23

24. Hyperbolic Identities
24
𝑐𝑜𝑠ℎ2𝑥 − 𝑠𝑖𝑛ℎ2𝑥 = 1
coth−1 𝑥 = tanh−1
1
𝑥
csch−1 𝑥 = sinh−1
1
𝑥
sech−1 𝑥 = cosh−1
1
𝑥
𝑡𝑎𝑛ℎ2𝑥 = 1 − 𝑠𝑒𝑐ℎ2𝑥
𝑠𝑖𝑛ℎ2𝑥 =
𝑐𝑜𝑠ℎ2𝑥 − 1
2
𝑐𝑜𝑠ℎ2𝑥 =
𝑐𝑜𝑠ℎ2𝑥 + 1
2
𝑐𝑜𝑠ℎ2𝑥 = 𝑐𝑜𝑠ℎ2
𝑥 − 𝑠𝑖𝑛ℎ2
𝑥
𝑠𝑖𝑛ℎ2𝑥 = 2 𝑠𝑖𝑛ℎ𝑥 𝑐𝑜𝑠ℎ𝑥

25. 𝐿. 𝐻. 𝑆 = 𝑐𝑜𝑠ℎ2
𝑥 − 𝑠𝑖𝑛ℎ2
𝑥
=
𝑒𝑥+𝑒−𝑥
2
2
−
𝑒𝑥−𝑒−𝑥
2
2
=
1
4
𝑒2𝑥
+ 2 + 𝑒−2𝑥
−
1
4
𝑒2𝑥
− 2 + 𝑒−2𝑥
=
1
4
2 + 2 =
4
4
= 1 = 𝑅. 𝐻. 𝑆
25
𝑐𝑜𝑠ℎ2
𝑥 − 𝑠𝑖𝑛ℎ2
𝑥 = 1

26. 𝐿𝑒𝑡 𝑦 = sech−1
𝑥
⇒ 𝑥 = 𝑠𝑒𝑐ℎ𝑦 =
1
𝑐𝑜𝑠ℎ𝑦
⇒ 𝑐𝑜𝑠ℎ𝑦 =
1
𝑥
⇒ 𝑦 = cosh−1
1
𝑥
⇒ sech−1
𝑥 = cosh−1
1
𝑥
26
sech−1
𝑥 = cosh−1
1
𝑥

27. Assignment
3.1
1.5.1. 𝑓 𝑥 = cos(tan−1 3)
1.5.2. 𝑓(𝑥) = sin(cos−1 2
2
)
1.5.3. 𝑓 𝑥 = sin−1 𝑠𝑖𝑛
𝜋
3
1.5.4. 𝑓(𝑥) = tan−1
tan −
𝜋
6
27
Evaluate the Following Functions

28. Assignment
3.2
1.4.1.1. 𝑓 𝑥 = 𝑥2 − 4 , 𝑥 ≥ 0
1.4.1.2. 𝑓 𝑥 =
3
𝑥 − 4
1.4.1.3. 𝑓 𝑥 = 𝑥3 + 1
1.4.1.4. 𝑓 𝑥 = 𝑥 − 1 2 , 𝑥 ≤ 1
1.4.1.5. 𝑓 𝑥 = 𝑥 − 1
1.4.1.6. 𝑓 𝑥 =
1
𝑥+2
1.4.1.7. 𝑓 𝑥 = 2𝑥 + 𝑙𝑛𝑥, find𝑓−1(2)
28
Find the inverse Functions and their domain
and range of the following expressions

29. Assignment
3.3
1.4.2.1. 𝑓 𝑥 = 8𝑥 , 𝑔 𝑥 =
𝑥
8
1.4.2.2. 𝑓 𝑥 = 8𝑥 + 3, 𝑔 𝑥 =
𝑥−3
8
1.4.2.3. 𝑓 𝑥 = 5𝑥 − 7, 𝑔 𝑥 =
𝑥+5
7
1.4.2.4. 𝑓 𝑥 =
2
3
𝑥 + 2, 𝑔 𝑥 =
3
2
𝑥 + 3
1.4.2.5. 𝑓 𝑥 =
1
𝑥−1
, 𝑥 ≠ 1, 𝑔 𝑥 =
1
𝑥
+ 1, 𝑥 ≠ 0
1.4.2.6. 𝑓 𝑥 = 𝑥3
+ 1 , 𝑔 𝑥 = 𝑥 − 1
1
3
1.4.2.7. 𝑓 𝑥 = 𝑥2 + 2𝑥 + 1, 𝑥 ≥ −1, 𝑔 𝑥 = −1 + 𝑥, 𝑥 ≥ 0
1.4.2.8. 𝑓 𝑥 = 4 − 𝑥2, 0 ≤ 𝑥 ≤ 2, 𝑔 𝑥 = 4 − 𝑥2, 0 ≤ 𝑥 ≤ 2
29
For the following exercises, use composition to
determine which pairs of functions are
inverses.