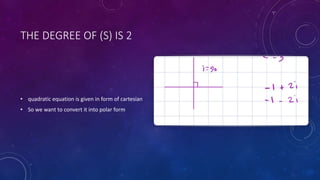
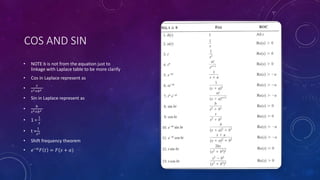
The document discusses the inverse Laplace transform focusing on converting functions from the s-domain to the time domain, particularly using complex roots and transformation rules. It elaborates on the simplification of quadratic equations from Cartesian to polar form and how coefficients affect the representation of sine and cosine in the Laplace transform. The process involves manipulating the equations through various operations to derive the inverse Laplace results related to specific terms like e^(-t) and integration techniques.

1. INVERSE LAPLACE
COMPLEX ROOTS
PREPARE BY TURKI NOUR

2. QUESTION IS
• F(s) to F(t)
• There are two cases
• This is case I

3. WE ARE LOOKING
AT DENOMINATOR
• And find the Coefficient numbers

4. THE DEGREE OF (S) IS 2
• quadratic equation is given in form of cartesian
• So we want to convert it into polar form

5. RULE OF CONVERSION
• We are using this rule to simplify the solution

6. K VALUE
• K value depend on the denominator of equation

7. IMPLEMENT OF
VALUES
• So b = -1 , and K= 4
• we get the value of parameters
• Now we goanna to put the values on
the rules or parameters

8. REPLACE
• We change the denominator to new
• So the equation become

9. WHY IT IS COMPLEX?
• We did the change from Cartesian
form into polar form
• J𝜔 is imaginary
• This will help us to identify the
inverse will contain sin or cos because
it is imaginary

10. COS AND SIN
• NOTE b is not from the equation just to
linkage with Laplace table to be more clarify
• Cos in Laplace represent as
•
𝑠
𝑠2+𝑏2
• Sin in Laplace represent as
•
𝑏
𝑠2+𝑏2
• 1 =
1
𝑠
• t =
1
𝑠2
• Shift frequency theorem
• 𝑒−𝑎
𝐹 𝑡 = 𝐹(𝑠 + 𝑎)

11. (S+1)
• We just taken (s+1) from
denominator to nominator

12. 2S+12
• After we put the (s+1) at the top
• We want (s+1) = 2s+12

13. 2(S+1)+10
• So by multiply 2 and add 10
• It become similar to old numerator

14. TAKING THE INVERSE L
• Because the denominator is the same
we apply addition of fraction rule
• Instead of number 4 we going to take
it as 22

15. TAKING THE INVERSE L
• Like this

16. TAKING THE INVERSE L
• Sin in Laplace represent as
•
𝑏
𝑠2+𝑏2
• So 10 not equal to 2
• So taken up the 2
• Also 10 divide it by 2

17. TAKING THE INVERSE L
• Why 𝑒−𝑡
?
• Because we have
1
(𝑠+1)2 (s+1) *2
• The remaining from the table