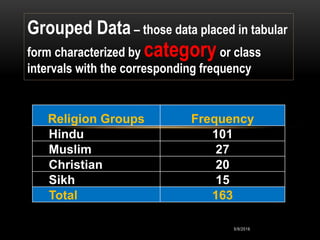
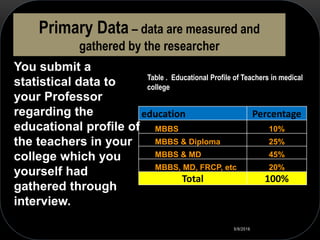
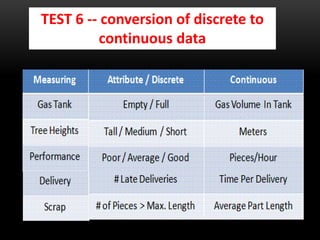
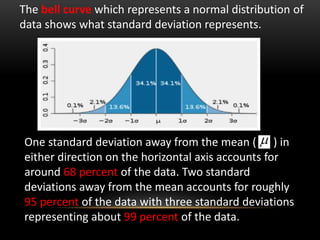
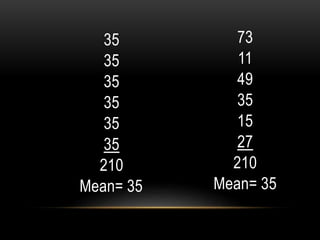
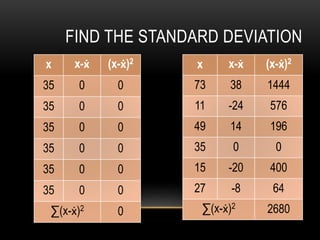
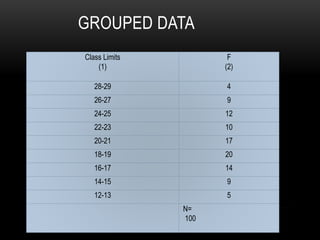
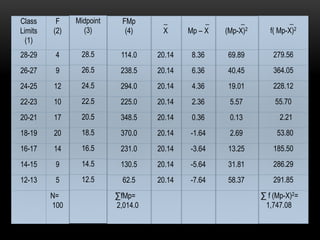
The document discusses standard deviation and variance in statistics. It defines standard deviation as a measure of how far data points are spread from the mean. A lower standard deviation indicates data points are close to the mean, while a higher standard deviation indicates data points are more spread out. It provides the formula for calculating standard deviation and explains the steps. Variance is defined as the average of the squared deviations from the mean and the formula is given. Grouped data and calculating variance from grouped data is also covered. Applications of standard deviation are listed.

1. PG Student :- Dr. Vinay Dange
Dr. Amol Askar
PG Teacher :- Dr. S. V. Akarte
Dr. D. Nandanwar
STANDARD DEVIATION &
VARIANCE

2. THINK OF THESE…
5/9/2016
• Crime rate
• Unemployment
figures
• 2010 BAR Passing
rate
• Mortality rates
• Net Reproduction
Rate
• Proportion of voters
favoring a candidate
• Enrolment trend
• Drop-out rate
• Number of Accident per
year
• Annual growth rate
• Monthly income
• Doctor population ratio
• Prevalence of disease
• Average life span
• Registered vehicles
annually
• Ratio of male teachers
to the female

3. 5/9/2016
Statistics
• Statistics is a branch of mathematics that deals with
the methods of collection, compilation, analysis,
presentation, and interpretation of data.
Biostatistics
• Is defined as application of statistical methods to
medical, biological and public health related
problems.

4. APPLICATIONS OF BIOSTATISTICS
• Assess community needs
• Understand socio-economic determinants of health
• Plan experiment in health research
• Analyse their results
• Study diagnosis and prognosis of the disease for taking
effective action
• Scientifically test the efficacy of new medicines and methods
of treatment.

5. 5/9/2016
 Descriptive Statistics
 Inferential Statistics
GENERAL CATEGORIES OF
STATISTICS

6. 5/9/2016
 It is concerned with the gathering,
classification, and presentation of data and
summarizing the values to describe the group
characteristic.
DESCRIPTIVE STATISTICS

7. 5/9/2016
 It pertains to the methods dealing with
making of inference, estimate or prediction
about a large set of data (population) using the
information gathered from a sample.
INFERENTIAL STATISTICS

8. Spot the
5/9/2016
Choose a sample…
Study the sample…
Describe the sample.
Descriptive Statistics
Choose a sample…
Study the sample…
Describe the sample…
Use such estimates( CONCLUSIONS) to
describe the population from where the
sample was drawn.
Inferential Statistics

9. 5/9/2016
•Population
 refers to entire group of people or study elements ---
animals, subjects, measurements, things of any form for
which we have an interest at a particular time.
•Samples
 are elements of the population selected through a
process.
 They have of the same characteristics with the
population.
POPULATION AND SAMPLE

10. • PARAMETER
This is the value that describes population or universe
• STATISTIC
 It is a measure that derived from sample, such as sample
mean, sample standard deviation
 This summary describes sample

11. POPULATION
SAMPLE
ILLUSTRATIO5/9/2016

12. 5/9/2016
DATA
• Qualitative Vs Quantitative data
• Grouped Data Vs Ungrouped data
• Primary data Vs Secondary Data
• Discrete Vs Continuous data
• Nominal Vs Ordinal
Data are any bits or collection of information,
ideas, figures or concepts.

13. RAW DATA – THOSE DATA IN THEIR
ORIGINAL FORM AND STRUCTURE
5/9/2016
When you ask 1st year residents about their age,
date of birth, ethnic group, religion, birth order,
occupation of his father, occupation of her
mother, educational background of his parents,
place of birth, ambition, favorite subject, most
liked Grade school teacher and hobbies – any
such information given by them will be
RAW DATA.

14. Grouped Data – those data placed in tabular
form characterized by categoryor class
intervals with the corresponding frequency
Religion Groups Frequency
Hindu 101
Muslim 27
Christian 20
Sikh 15
Total 163
5/9/2016

15. Primary Data – data are measured and
gathered by the researcher
You submit a
statistical data to
your Professor
regarding the
educational profile of
the teachers in your
college which you
yourself had
gathered through
interview.
education Percentage
MBBS 10%
MBBS & Diploma 25%
MBBS & MD 45%
MBBS, MD, FRCP, etc 20%
Total 100%
Table . Educational Profile of Teachers in medical
college
5/9/2016

16. Comparison of continuous and discrete data
•Continuous data is more precise than discrete
•Continuous data is more informative than discrete
•Continuous data can remove estimation and
rounding of measurements
•Continuous data is often more time consuming to
obtain
•Discrete should also be converted to continuous data
when possible as to obtain a higher level of
information and detail

18. • For each orange tree, the number of
oranges is measured.
TEST 1
–Quantitative
• For a particular day, the number of cars
entering a college campus is measured.
• Time until a light bulb burns out (4 months)
–Quantitative
–Quantitative

19. • blue/green color, gold frame
• smells old and musty
• texture shows brush strokes of oil
paint
• peaceful scene of the country
• masterful brush strokes
• picture is 10" by 14"
• with frame 14" by 18"
• weighs 8.5 pounds
• surface area of painting is
140 sq. in.
• cost $300
Quantitative data
Qualitative data
TEST 2 – Oil Painting

20. • Students
• Girls
• Smart/Intelligent
• Hard working
• 32 students
• 10 A grades
• 92% students Muslim by
religion
• 15 students good in
mathematics
Qualitative data
Quantitative data
TEST 3 -- Class

21. TEST 4 – conversion of quantitative
data to qualitative data
Haemoglobin level in Gm%
Hypo, Normo or hypertensiveBlood pressure in mm of Hg
Tall or ShortHeight in cm
Anaemic or Non anaemic
IQ scores Idiot, Genius, Normal
Qualitative dataQuantitative data

22. Classify each set of data as discrete or continuous.
• 1) The number of suitcases lost by an airline.
• 2) The height of corn plants.
• 3) The distance of your house to gym.
• 4) The time it takes for a car battery to die.
• 5) The production of tomatoes by weight.
TEST 5

23. TEST 6 -- conversion of discrete to
continuous data

24. • Religion Qualitative , Nominal data
• Disability Ordinal data
• Main food corps
• military rank (General,
colonel, major, etc.),
• Anxiety level
TEST 7
Ordinal data
Ordinal data
Nominal data
• IQ Interval data
• Stethoscope units sold Ratio data

25. Example: Two ways of asking about Smoking
behavior. Which is better, A or B? & why?
a) Do you smoke? Yes No
b) How many cigarettes did you smoke in the last 3
days (72 hours)?
(a) Is nominal, so the best we can get from this data
are frequencies.
(b) is ratio, so we can compute: mean, median,
mode, frequencies.
TEST 8

26. Method of determining class intervals

27. Size of Class Interval

28. Mean
Median
Mode
Measures of Central Tendency

29. Measures of dispersion / variability
 Range
 Interquartile range
 Mean deviation
 Standard deviation
 Coefficient of variation

30. STANDARD DEVIATION
 is a special form of average deviation from the mean.
 is the positive square root of the arithmetic mean of
the squared deviations from the mean of the
distribution.
 is considered as the most reliable measure of
variability.
 is affected by the individual values or items in the
distribution.

31. STANDARD DEVIATION
Standard Deviation shows the variation in data.
If the data is close together, the standard
deviation will be small. If the data is spread out,
the standard deviation will be large.
Standard Deviation is often denoted by the lowercase
Greek letter sigma, . 

32. The bell curve which represents a normal distribution of
data shows what standard deviation represents.
One standard deviation away from the mean ( ) in
either direction on the horizontal axis accounts for
around 68 percent of the data. Two standard
deviations away from the mean accounts for roughly
95 percent of the data with three standard deviations
representing about 99 percent of the data.


33. STANDARD DEVIATION FORMULA
The standard deviation formula can be represented
using Sigma Notation:
2
( )x
n



 

34. STANDARD DEVIATION
1) Find the mean of the data.
2) Subtract the mean from each observation.
3) Square each deviation of the mean.
4) Find the sum of the squares.
5) Divide the total by the number of items.
6) Take the square root of the value.

35. VARIANCE
Variance is the average squared
deviation from the mean of a set of
data. It is used to find the standard
deviation.

36. VARIANCE FORMULA
2
( )x
n

The variance formula includes the Sigma
Notation, , which represents the sum of
all the items to the right of Sigma.

Mean is represented by and n is the
number of items.


37. VARIANCE
1. Find the mean of the data.
5. Divide the total by the number of items.
4. Find the sum of the squares.
3. Square each deviation of the mean.
2. Subtract the mean from each value – the
result is called the deviation from the mean.

38. 35
35
35
35
35
35
210
Mean= 35
73
11
49
35
15
27
210
Mean= 35

39. x x-ẋ (x-ẋ)2
35 0 0
35 0 0
35 0 0
35 0 0
35 0 0
35 0 0
∑(x-ẋ)2
0
FIND THE STANDARD DEVIATION
x x-ẋ (x-ẋ)2
73 38 1444
11 -24 576
49 14 196
35 0 0
15 -20 400
27 -8 64
∑(x-ẋ)2
2680

40. FIND THE STANDARD DEVIATION

41. Class Limits
(1)
F
(2)
28-29 4
26-27 9
24-25 12
22-23 10
20-21 17
18-19 20
16-17 14
14-15 9
12-13 5
N=
100
GROUPED DATA

42. VARIANCE FOR GROUPED DATA
Variance for Ungrouped Data

43. _
f( Mp-X)2
279.56
364.05
228.12
55.70
2.21
53.80
185.50
286.29
291.85
∑ f (Mp-X)2=
1,747.08
_
(Mp-X)2
69.89
40.45
19.01
5.57
0.13
2.69
13.25
31.81
58.37
_
Mp – X
8.36
6.36
4.36
2.36
0.36
-1.64
-3.64
-5.64
-7.64
_
X
20.14
20.14
20.14
20.14
20.14
20.14
20.14
20.14
20.14
FMp
(4)
114.0
238.5
294.0
225.0
348.5
370.0
231.0
130.5
62.5
∑fMp=
2,014.0
Midpoint
(3)
28.5
26.5
24.5
22.5
20.5
18.5
16.5
14.5
12.5
Class
Limits
(1)
F
(2)
28-29 4
26-27 9
24-25 12
22-23 10
20-21 17
18-19 20
16-17 14
14-15 9
12-13 5
N=
100

44. FIND THE STANDARD DEVIATION

45. APPLICATIONS OF SD
• A SD is universally accepted unit of dispersion of values from
mean value
• SD summarises the variation of large distribution and defines
normal limits of variation.
• SD measures position or distance of observation from mean
• SD indicates whether the variation of difference of an individual
from mean is by chance.
• SD is used to calculate standard error of mean and SE of
difference between 2 means
• SD helps to find the size of sample
• SD is used to calulate relative deviate or Z score
• SD is used in calcualtion of coefficient of variation

46.  Merits of SD
 It is rigidly defined
 It is based on all observations
 It is not much affected by sampling fluctuations.
 Demerits of SD
 It is difficult to understand and calculate
 It can not be calculated for qualitative data
 It is unduly affected by extreme deviations

47. FIND THE VARIANCE AND
STANDARD DEVIATION
The math test scores of five students are:
92,88,80,68 and 52.
1) Find the mean: (92+88+80+68+52)/5 = 76.
2) Find the deviation from the mean:
92-76=16
88-76=12
80-76=4
68-76= -8
52-76= -24

48. 3) Square the deviation from the
mean:
2
( 8) 64 
2
(16) 256
2
(12) 144
2
(4) 16
2
( 24) 576 
The math test scores of five students are:
92,88,80,68 and 52.

49. The math test scores of five students are:
92,88,80,68 and 52.
4) Find the sum of the squares of the deviation
from the mean:
256+144+16+64+576= 1056
5) Divide by the number of data items to
find the variance:
1056/5 = 211.2

50. The math test scores of five students are:
92,88,80,68 and 52.
6) Find the square root of the
variance: 211.2 14.53
Thus the standard deviation of the test
scores is 14.53.

51. DISCRETE AND CONTINUOUS DATA
• There are two types of Quantitative Data:
• 1. Discrete (in whole numbers)
• Exp: Number of Questions in Exam 5, 7, 14
• Number of cars,
• Number of students 3000
• 2. Continuous (in decimal points)
Exp: Temperature of Yanbu on Sunday 26.5 degrees
• Your Height 5.3”
• Your Weight 120.5 lbs