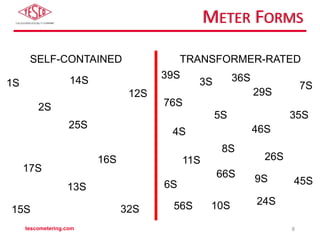
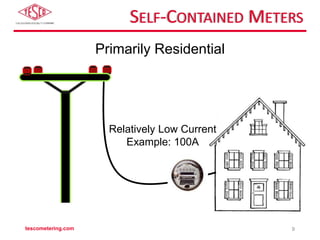
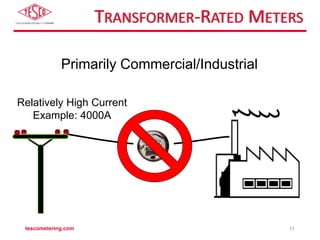
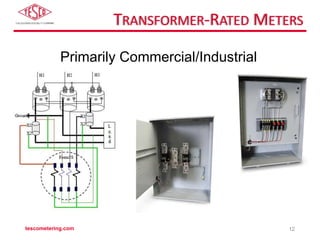
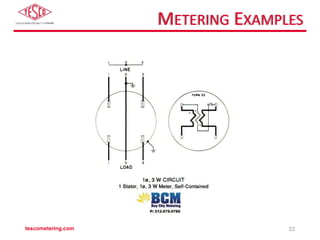
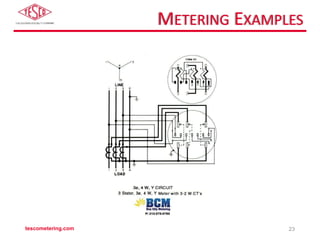
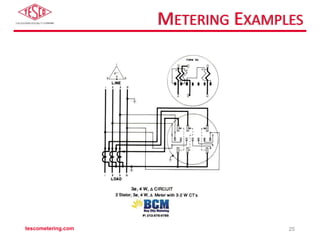
The document discusses the differences between self-contained and transformer-rated meter forms, detailing their functionality and underlying principles, including Blondel's theorem. It offers an overview of electro-mechanical and solid-state meters, highlighting their operating mechanisms and typical applications. Multiple meter forms and references for further reading are provided, underscoring the importance of accurate power measurement in electrical systems.