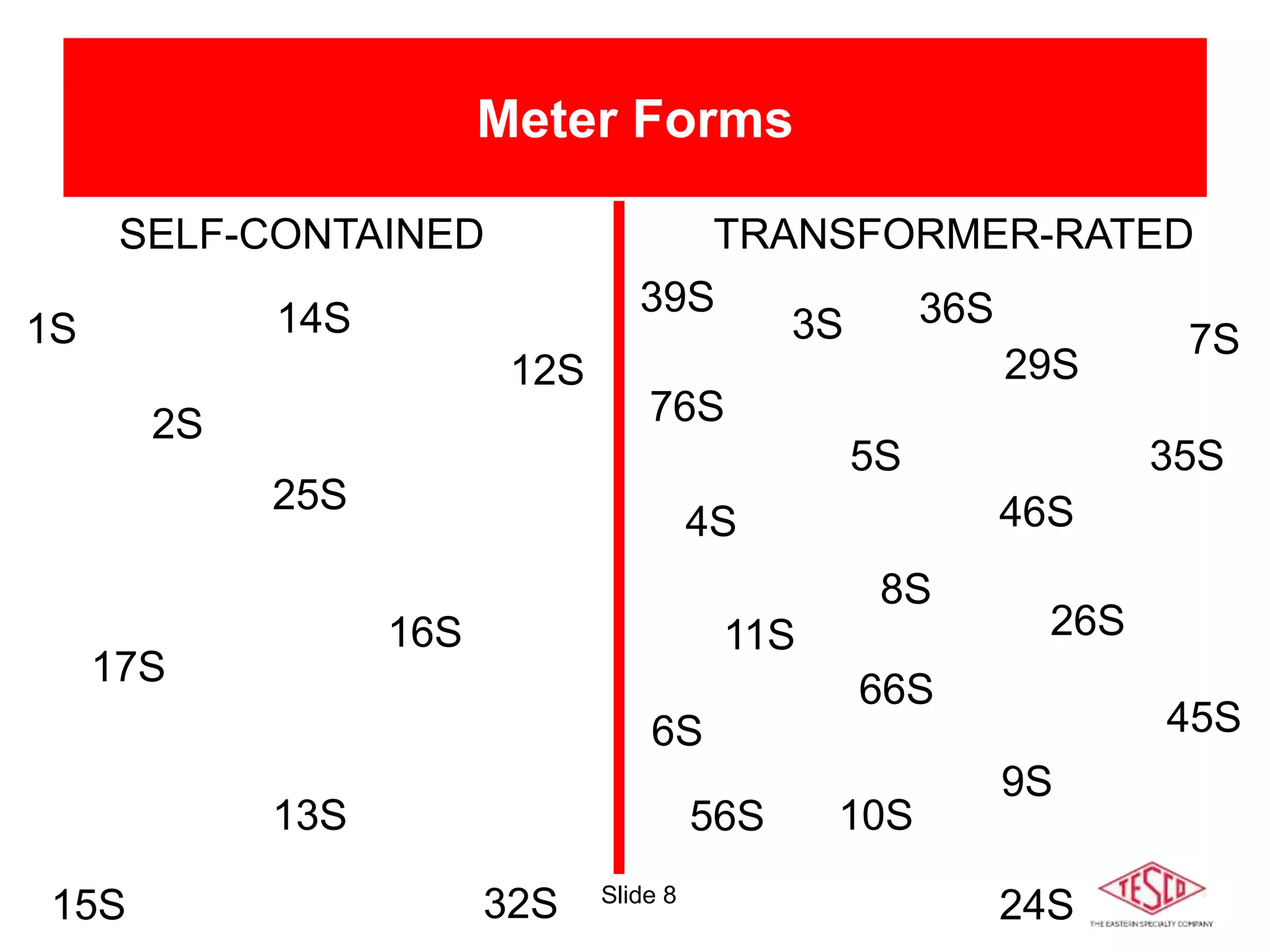
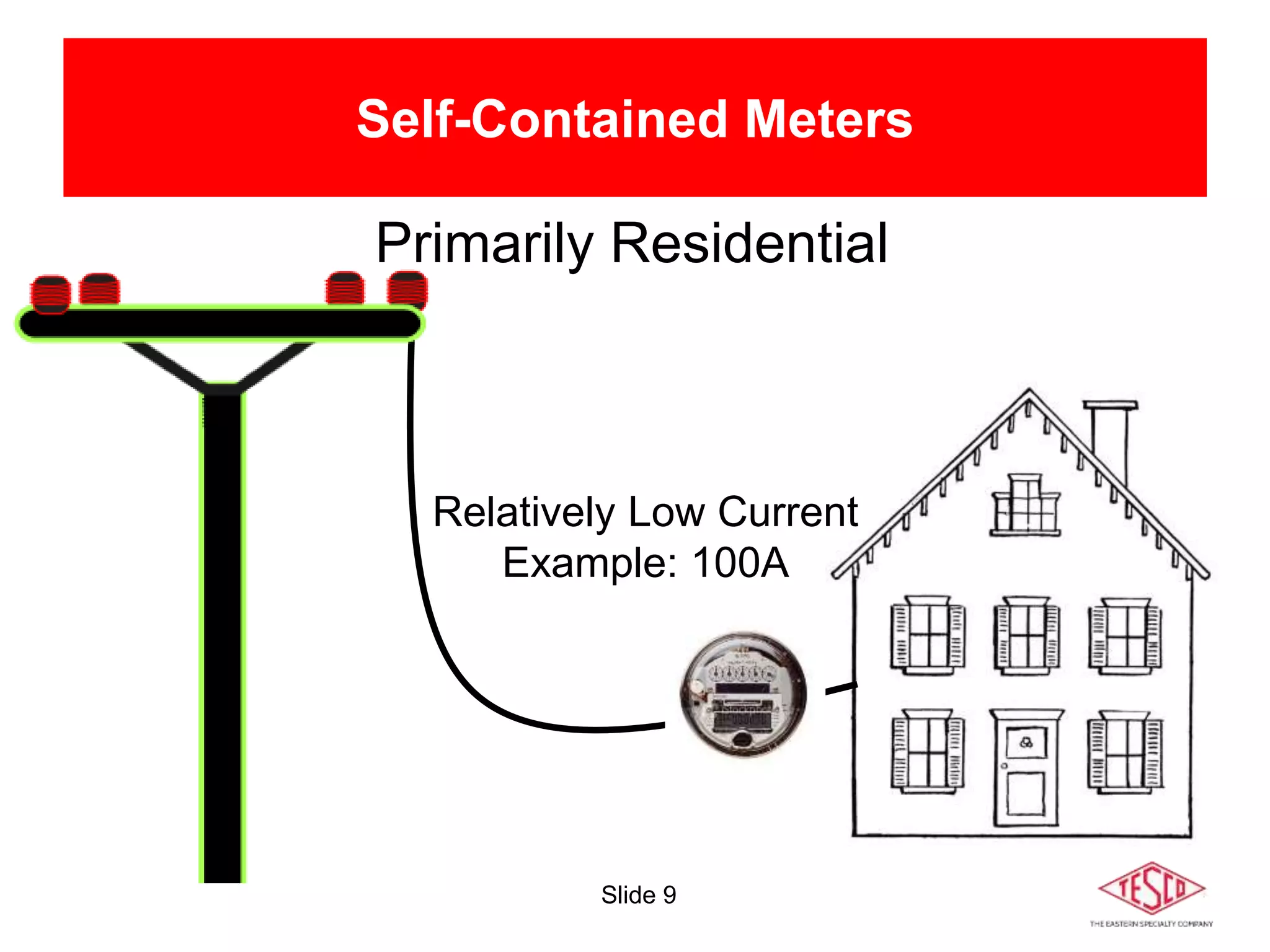
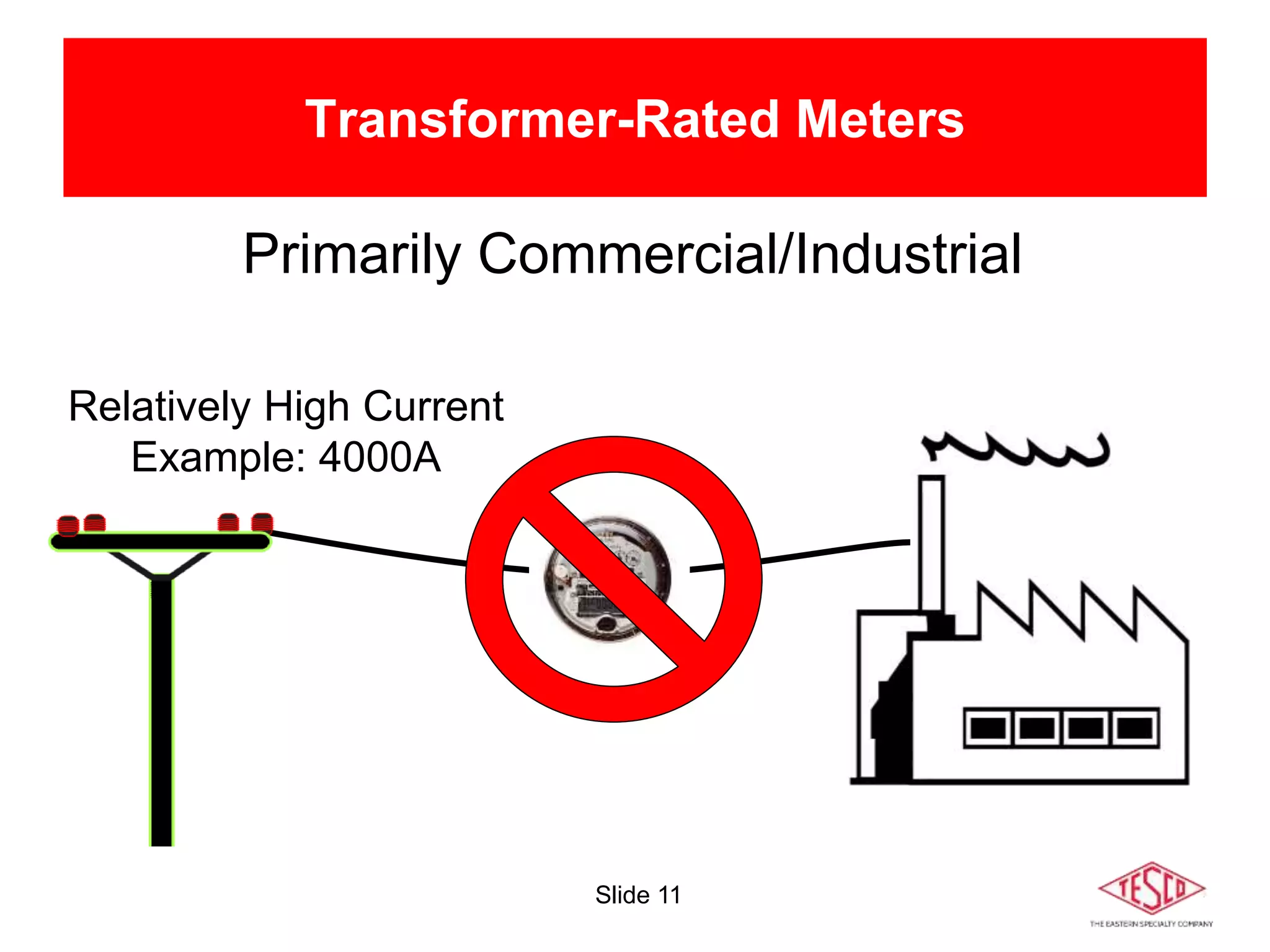
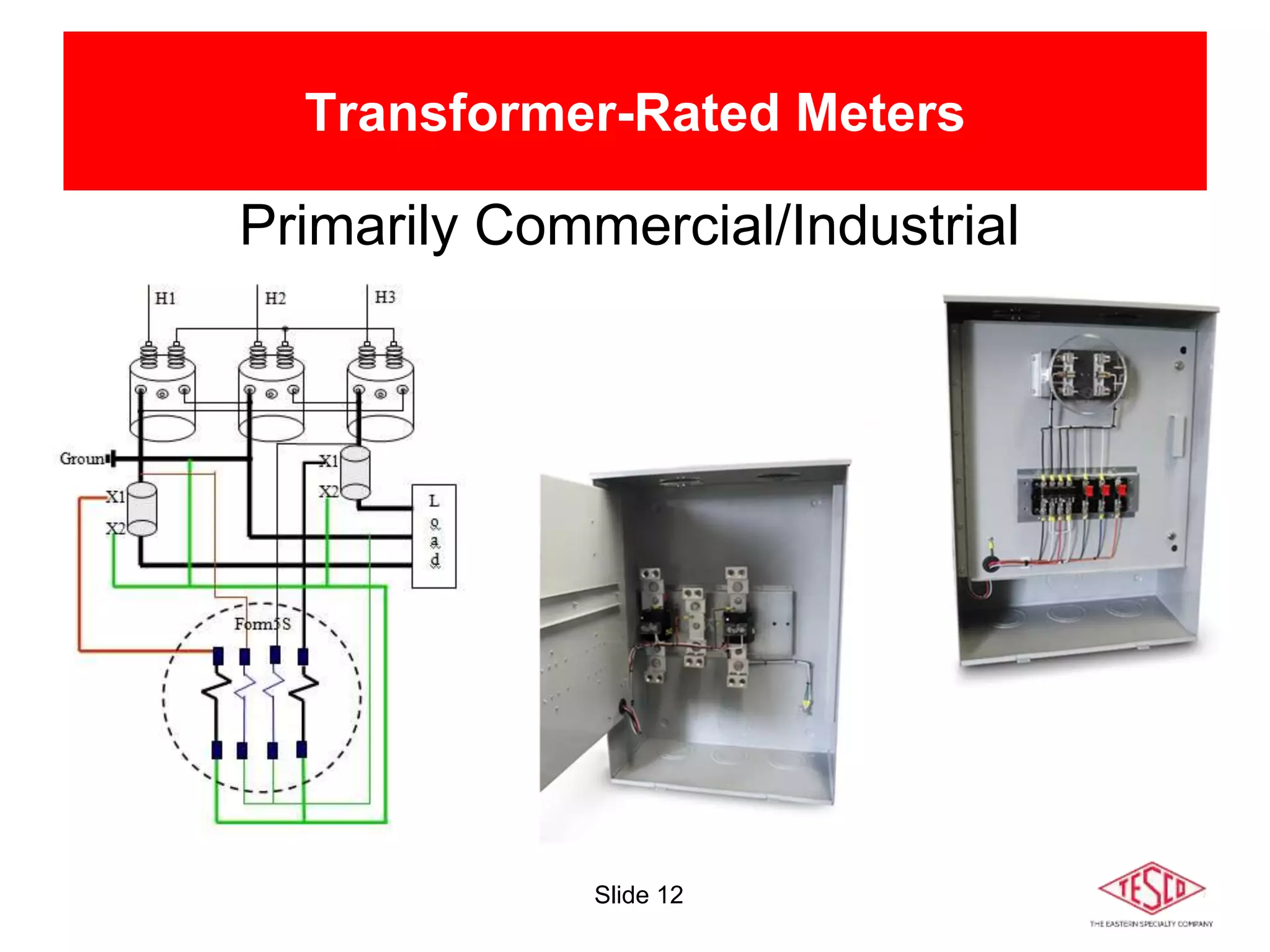
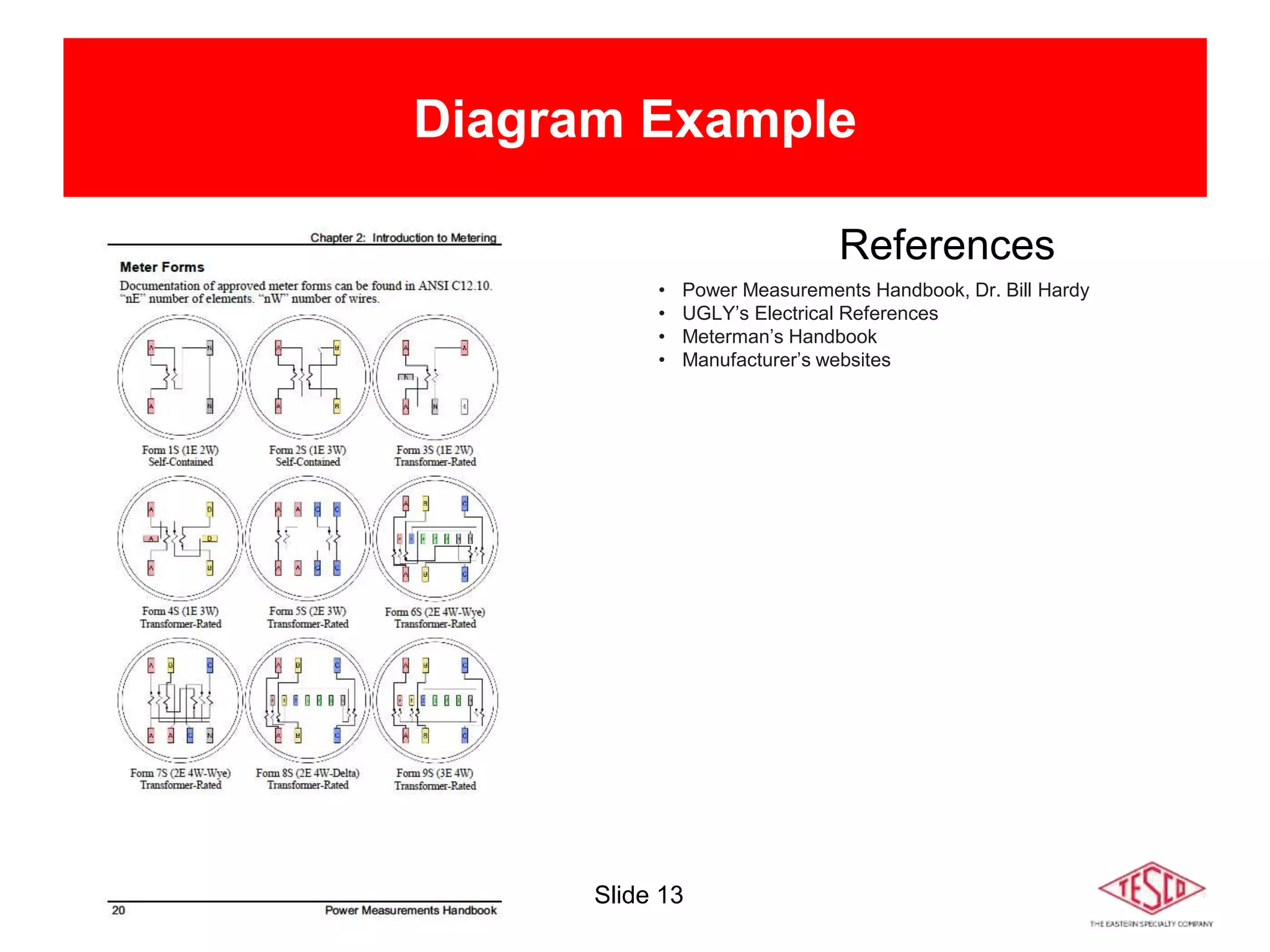
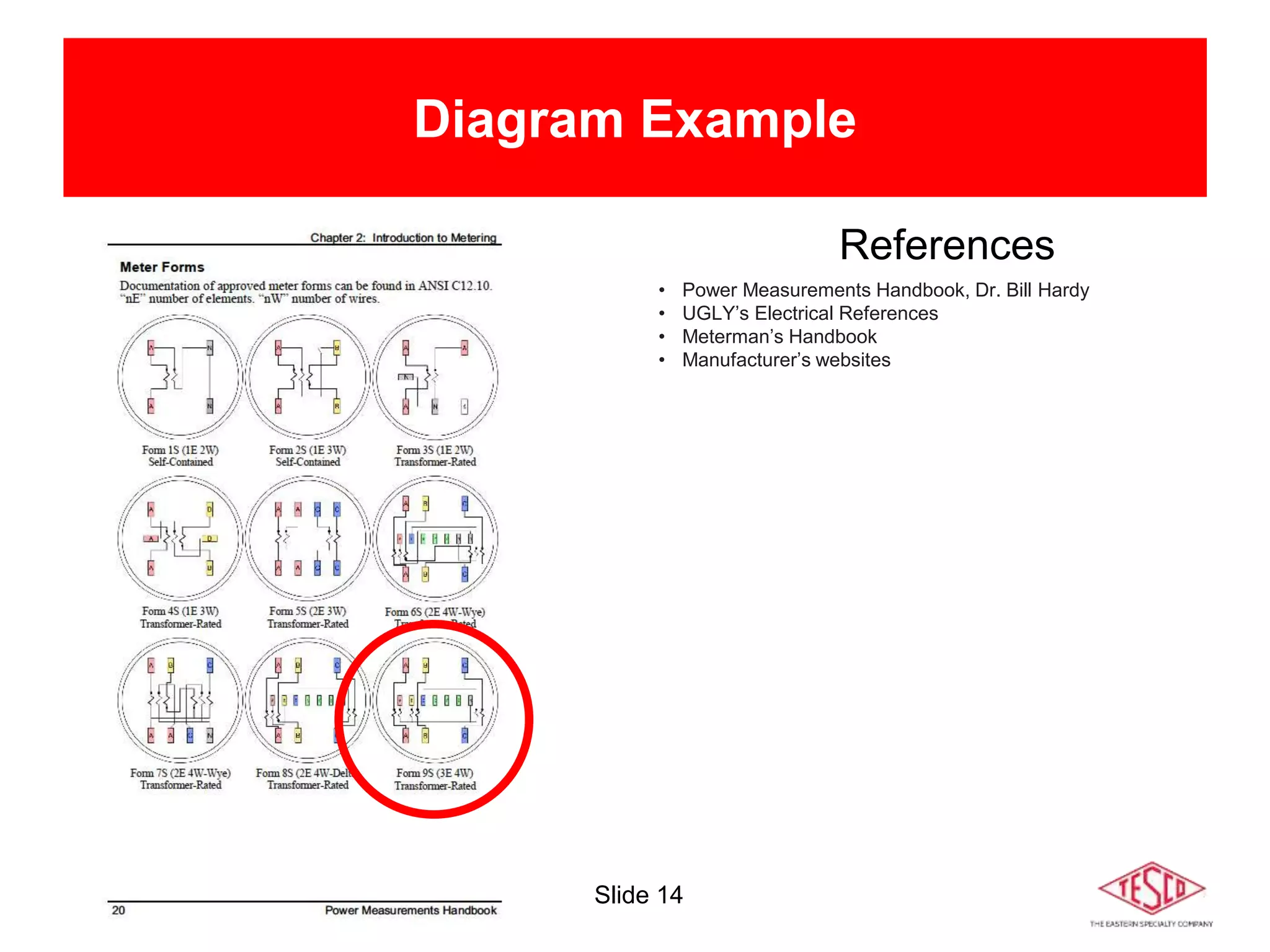
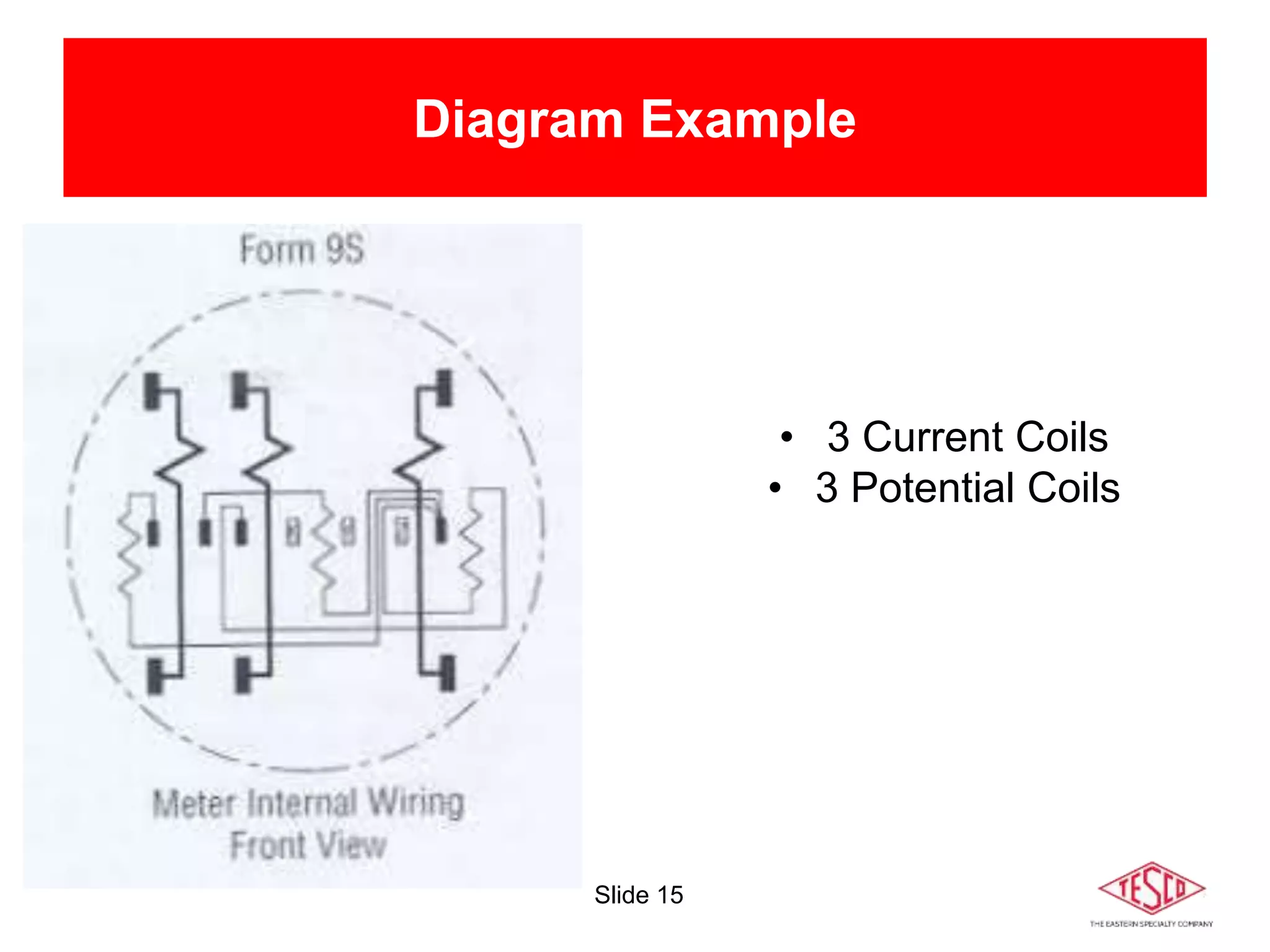
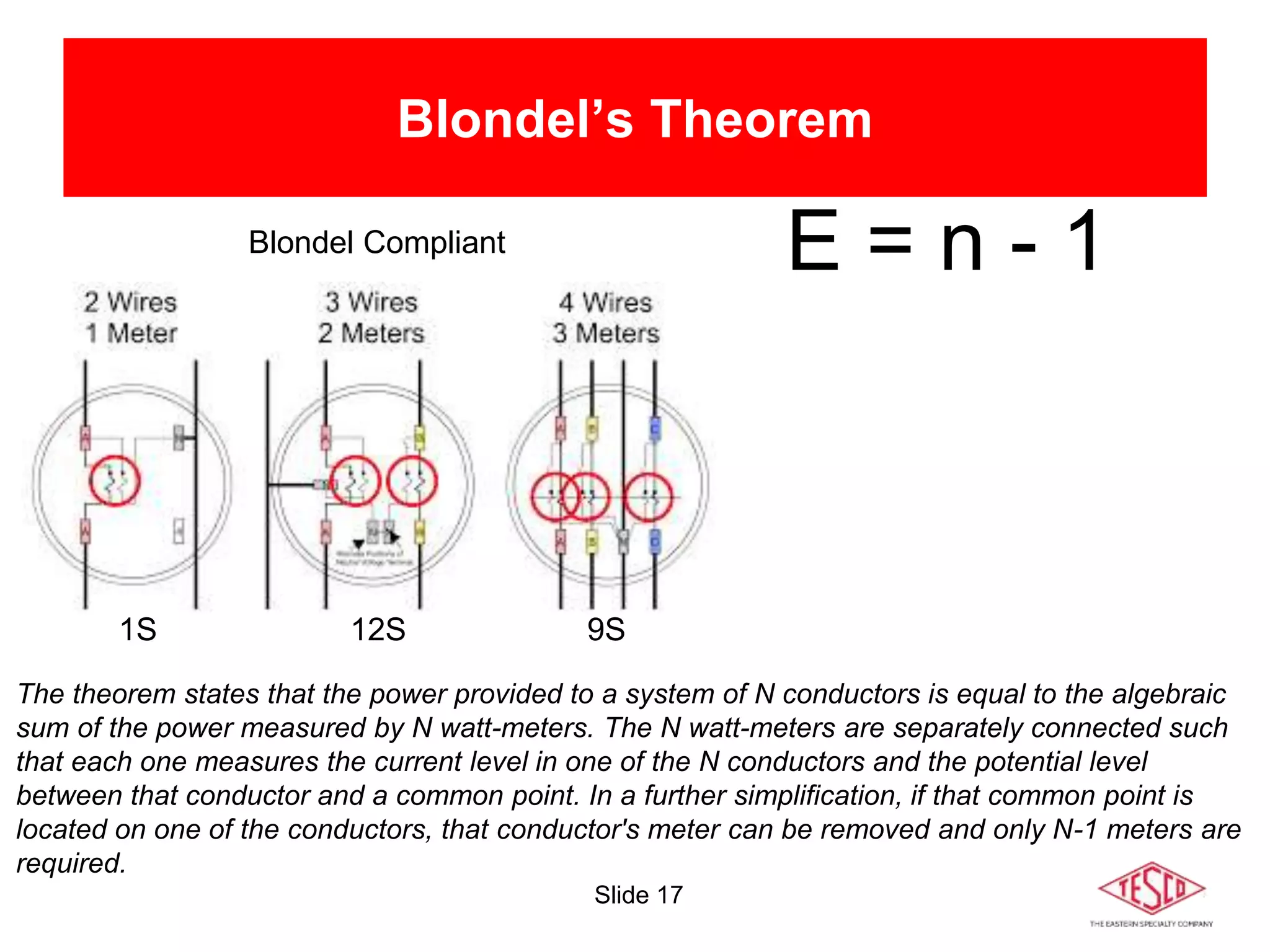
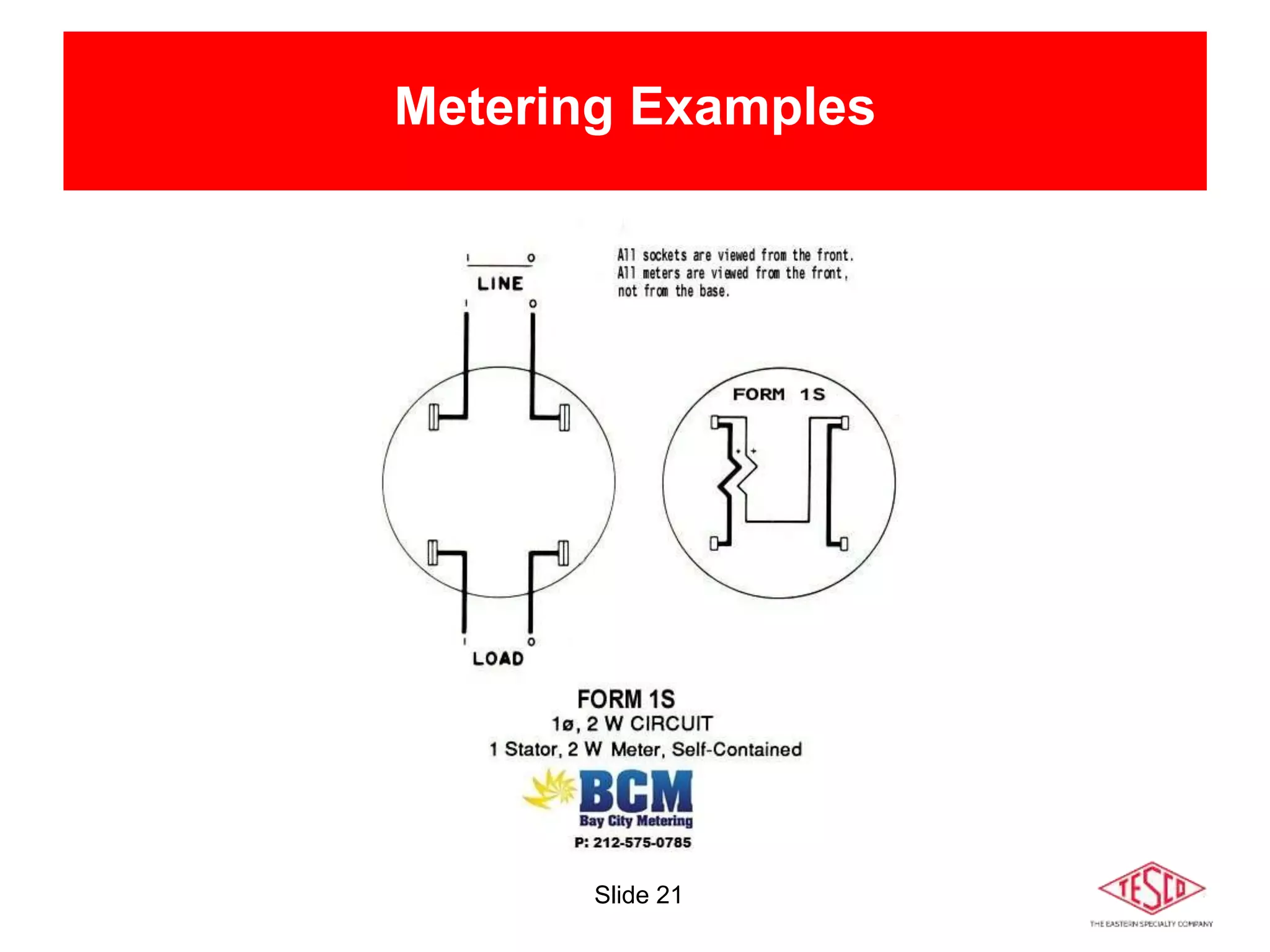
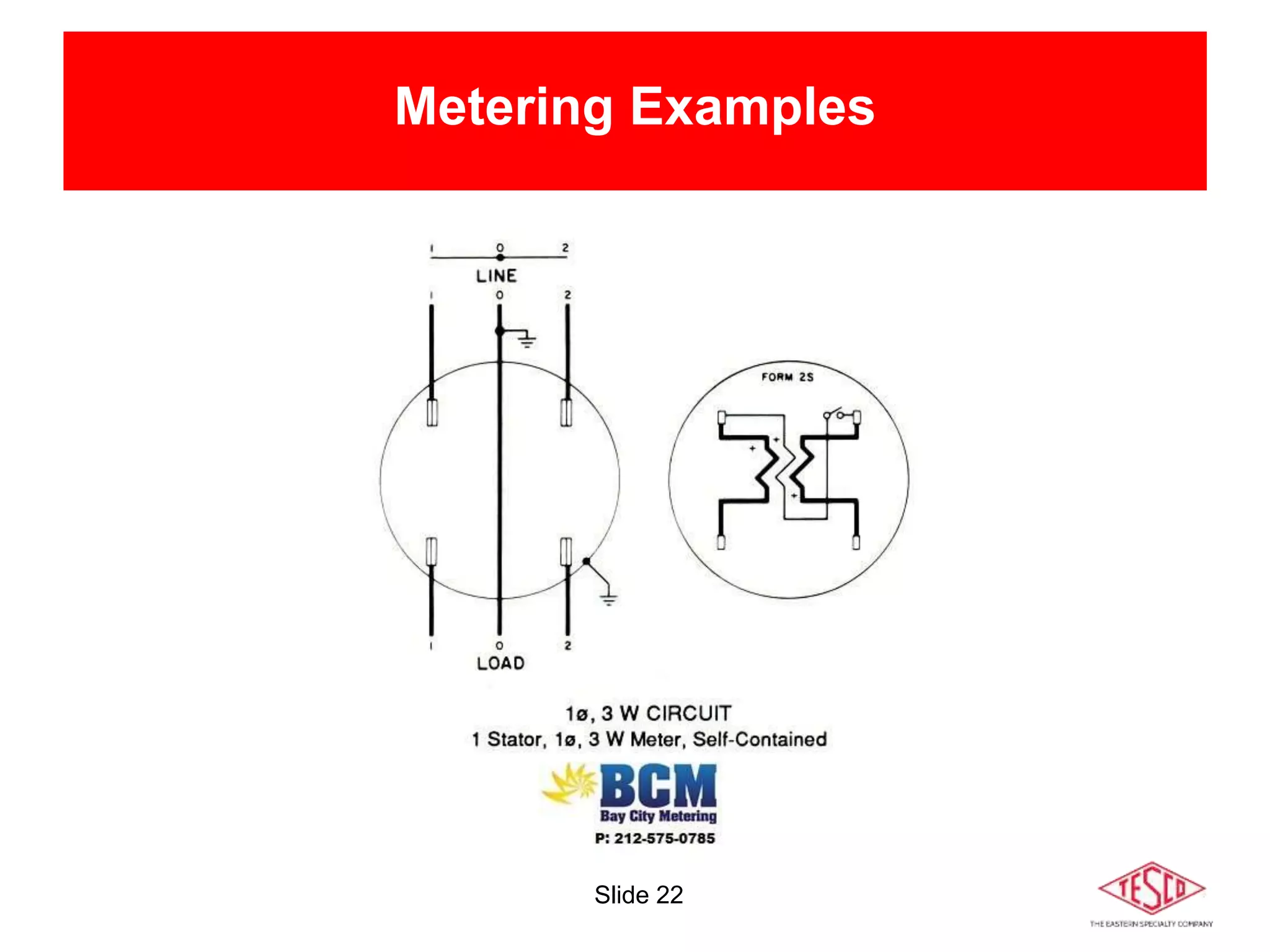
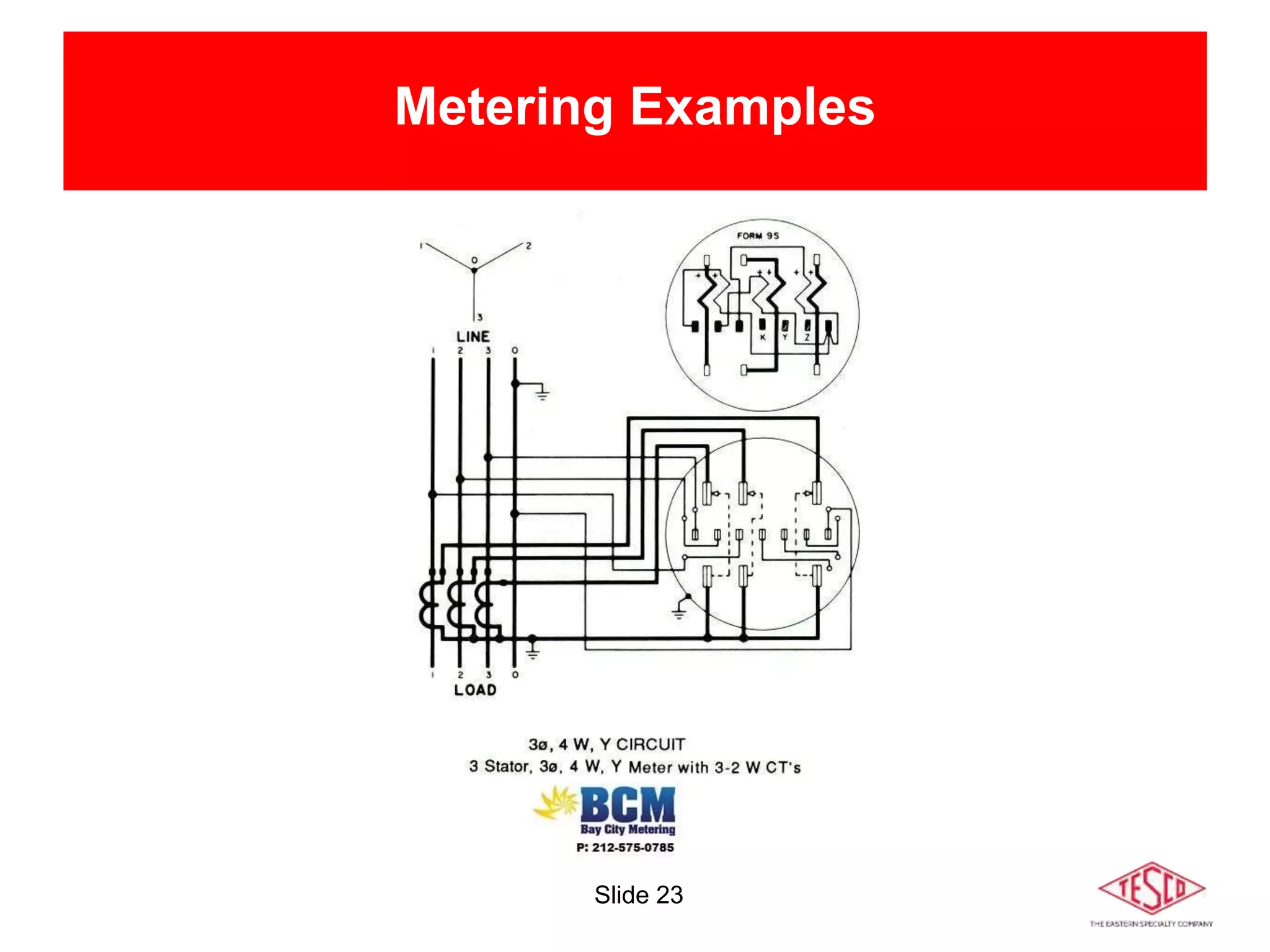
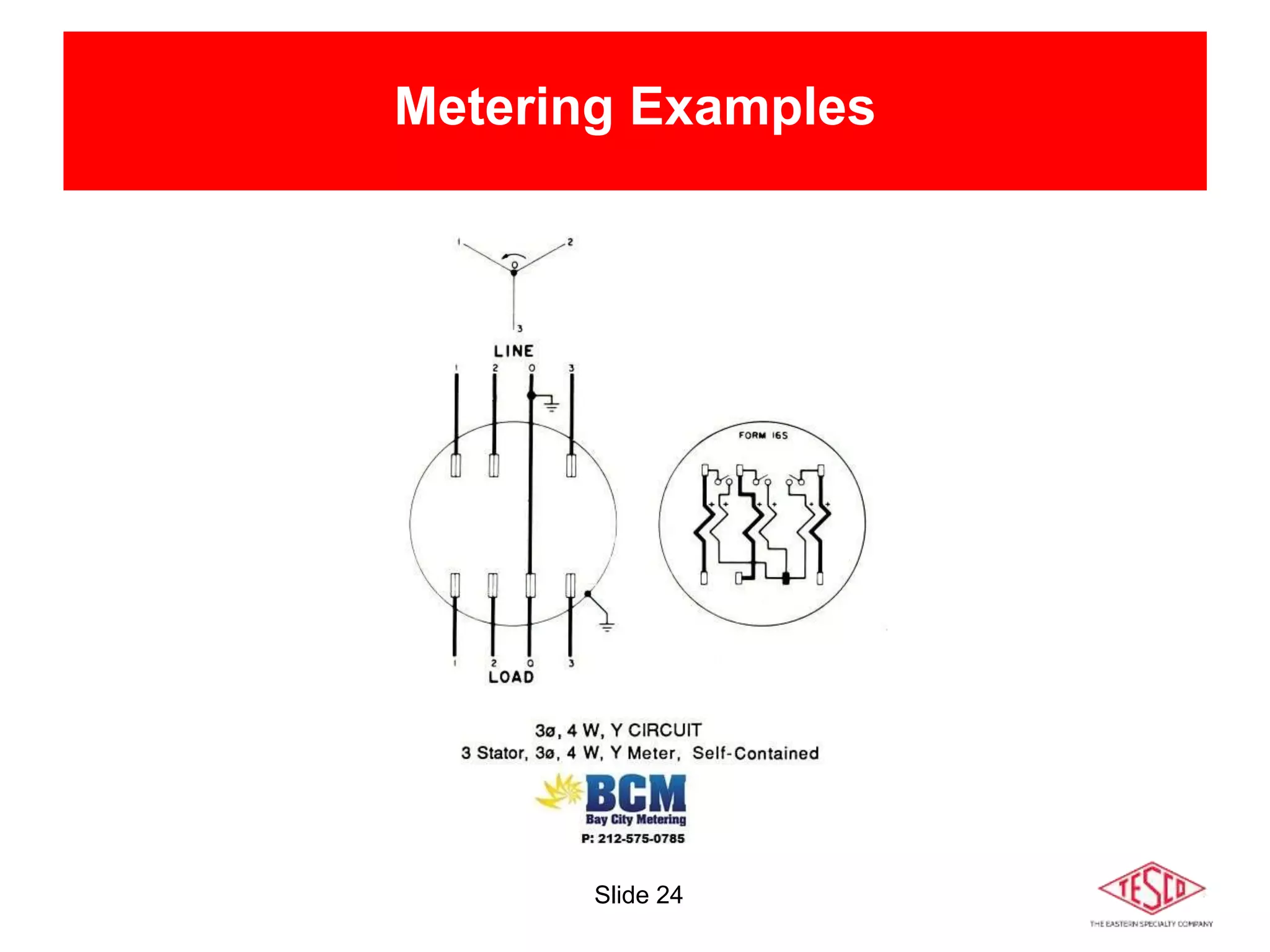
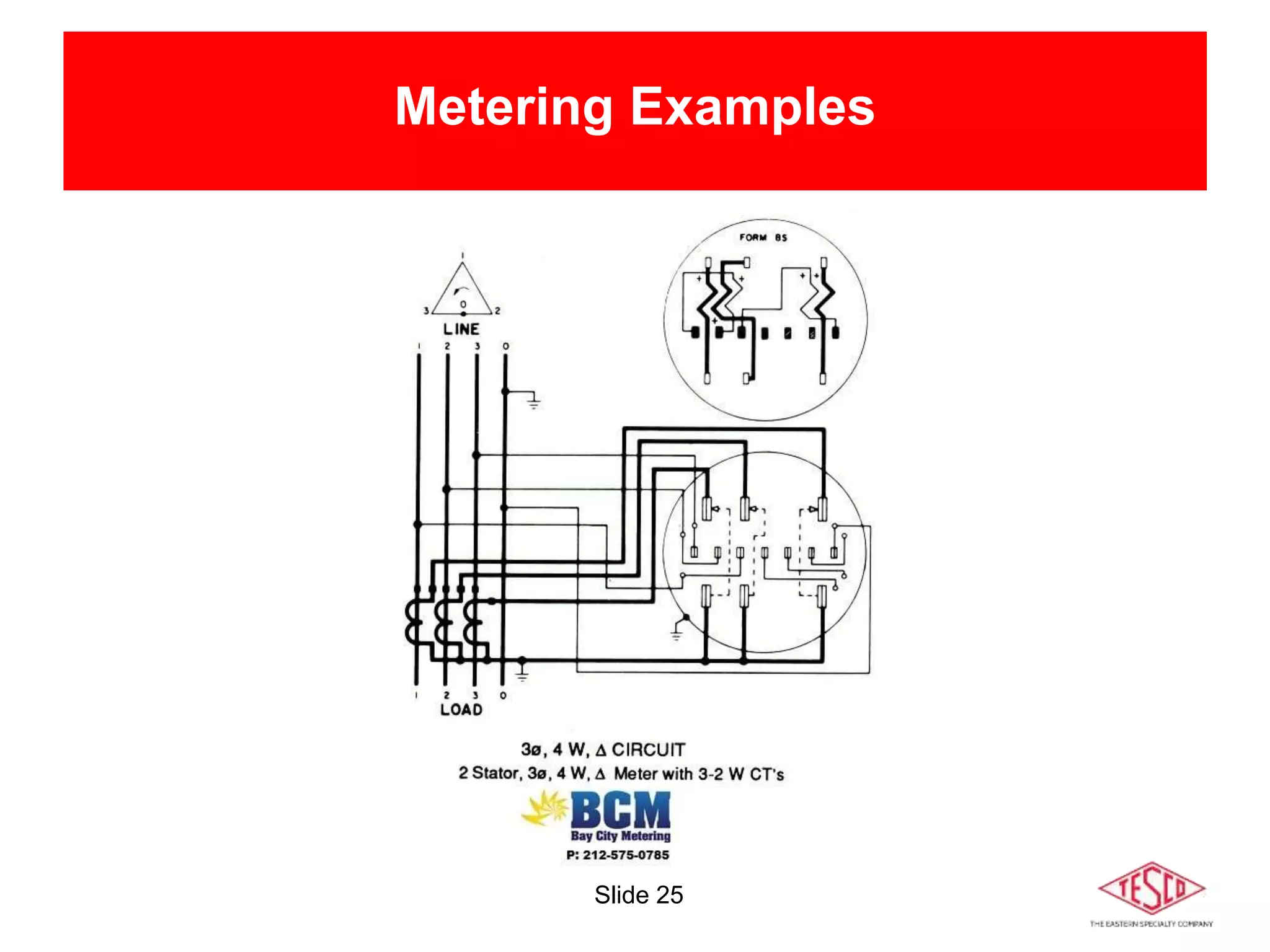
The document is a presentation on meter forms and their functionalities, covering electro-mechanical and solid-state meters, including self-contained and transformer-rated types. It introduces Blondel's theorem for measuring power in electrical systems and discusses various meter examples and references. Additionally, it emphasizes the differences between compliant and non-compliant metering practices, along with their implications for measurement accuracy.