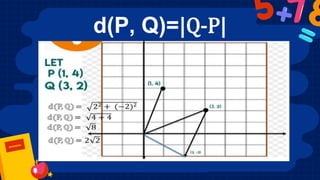
This document discusses inner product spaces and properties of the inner product. It provides examples of determining the inner product of vectors and applying properties like commutativity, distributivity, and associativity. It also defines length in Rn and discusses the Euclidean plane E2, defining distance between points as the absolute value of their difference. Students will learn to determine if a function defines an inner product, find inner products of vectors, and solve for distances in E2.

4. INNER PRODUCT
SPACE
REPORTER: MARK A. SOLIVA

5. At the end of the lesson the students will be able to:
 Determine whether a function defines an inner
product.
 Find the inner product of two vector in 𝑅𝑛.
OBJECTIVES

6. INNER-PRODUCT SPACE
It is represented by angle
brackets <u, v>
It is a vector space with additional
structure called an inner product.
It is a function that associate a
real number <u, v> that satisfies
the following axioms…

7. PROPERTIES OF INNER PRODUCT
 Commutative Property of the Inner Product ( <u, v> = (v, u> )
 Distributive Property of the Inner Product (<u, v+w>=<u, v>+<u, w>)
 Associative Property of Inner Product ( k<u, v>=<ku, v>)
 Positive Semi-Definite < 𝑣, 𝑣 > ≥ 0 if and only if v = 0
 Point-Separate/Non-Degenerate < 𝑣, 𝑣 > = 0 if and only if v = 0

8. Commutative Property of the Inner
Product (<u, v> = <v, u>)
Example 1: 𝑢 = 𝑢1, 𝑢2, … 𝑢𝑛
𝑣 = (𝑣1, 𝑣2, … 𝑣𝑛)
Solution:
< 𝑢, 𝑣 > = 𝑢1𝑣1 + 𝑢2𝑣2 + ⋯ + 𝑢𝑛𝑣𝑛

9. 1. Commutative Property of the Inner Product (<u, v>=<v , u>)
Example 2: u = (2, 3)
v = (-1, 2)
Solution: (<u, v>=<v, u>)
𝒖𝟏𝒗𝟏 + 𝒖𝟐𝒗𝟐 = 𝒗𝟏𝒖𝟏 + 𝒗𝟐𝒖𝟐
(2*-1)+(3*2)=(-1*2)+(2*3)
-2+6=-2+6
4=4

10. Commutative Property of the Inner Product (<u,
v> =<v, u>)
Example 3: u = (0, -5, 2)
v= (6, 9, 0)
Solution:
< 𝒖, 𝒗 > = 𝒖𝟏𝒗𝟏 + 𝒖𝟐𝒗𝟐 + 𝒖𝟑𝒗𝟑
< 𝒖, 𝒗 > = 𝟎 ∗ 𝟔 + −𝟓 ∗ 𝟗 + 𝟐 ∗ 𝟎 = −𝟒𝟓

11. DISTRIBUTIVE PROPERTY OF THE INNER
PRODUCT
(<u, v+w>=<u, v>+<u, w>)
Example: u= (2, 3) k= 2
v= (-1, 2) w=(3, 1) v+w = (2, 3)
Solution:
(<u, v+w>=<u, v>+<u, w>)
𝒖𝟏(𝒗 + 𝒘)𝟏+𝒖𝟐(𝒗 + 𝒘)𝟐= 𝒖𝟏𝒗𝟏 + 𝒖𝟐𝒗𝟐 + 𝒖𝟏𝒘𝟏 + 𝒖𝟐𝒘𝟐
𝟐 ∗ 𝟐 + 𝟑 ∗ 𝟑 = 𝟐 ∗ −𝟏 + 𝟑 ∗ 𝟐 + 𝟐 ∗ 𝟑 + 𝟑 ∗ 𝟏
𝟒 + 𝟗 = −𝟐 + 𝟔 + 𝟔 + 𝟑
𝟏𝟑 = 𝟏𝟑

12. DISTRIBUTIVE PROPERTY OF THE INNER
PRODUCT
(<u, v+w>=<u, v>+<u, w>)
EXAMPLE 2: u=(0, -1) w=(-1,2)
v=(2,-3) v+w=(1,-1)
Solution:
(<u, v+w>=<u, v>+<u, w>)
𝒖𝟏(𝒗 + 𝒘)𝟏+𝒖𝟐(𝒗 + 𝒘)𝟐= 𝒖𝟏𝒗𝟏 + 𝒖𝟐𝒗𝟐 + 𝒖𝟏𝒘𝟏 + 𝒖𝟐𝒘𝟐
𝟎 ∗ 𝟏 + −𝟏 ∗ −𝟏 = 𝟎 ∗ 𝟐 + −𝟏 ∗ −𝟑 + 𝟎 ∗ −𝟏 + −𝟏 ∗ 𝟐
𝟎 + 𝟏 = 𝟎 + 𝟑 + 𝟎 + (−𝟐)
𝟏 = 𝟏

13. ASSOCIATIVE PROPERTY OF INNER PRODUCT
(k<u, v>=<ku, v>)
Example : 1 u=(2, 3) k=2
v=(-1, 2) ku=(4,6)
Solution:
𝒌 < 𝒖, 𝒗 > = < 𝒌𝒖, 𝒗 >
𝒌 𝒖𝟏𝒗𝟏 + 𝒖𝟐𝒗𝟐 = 𝒌𝒖𝟏𝒗𝟏 + 𝒌𝒖𝟐𝒗𝟐
𝟐 𝟐 ∗ −𝟏 + 𝟑 ∗ 𝟐 = 𝟒 ∗ −𝟏 + 𝟔 ∗ 𝟐
𝟐 −𝟐 + 𝟔 = −𝟒 + 𝟏𝟐
𝟖 = 𝟖

14. ASSOCIATIVE PROPERTY OF INNER
PRODUCT (k<u, v>=<ku, v>)
Example 2: u=(0, 1) k=3
v=(2,3) ku=(0,3)
Solution: 𝒌 < 𝒖, 𝒗 > = < 𝒌𝒖, 𝒗 >
𝒌 𝒖𝟏𝒗𝟏 + 𝒖𝟐𝒗𝟐 = 𝒌𝒖𝟏𝒗𝟏 + 𝒌𝒖𝟐𝒗𝟐
𝟑 𝟎 ∗ 𝟐 + 𝟏 ∗ 𝟑 = 𝟎 ∗ 𝟐 + 𝟑 ∗ 𝟑
𝟑 𝟎 + 𝟑 = 𝟎 + 𝟗
𝟗 = 𝟗

15. 𝑳𝑬𝑵𝑮𝑻 𝑰𝑵 𝑹𝒏

16. 𝑳𝑬𝑵𝑮𝑻𝑯 𝑰𝑵 𝑹𝒏
Example 1: v=(0, -2, 1, 4, -2)
𝒗 = 𝟎𝟐 + −𝟐𝟐 + 𝟏𝟐 + 𝟒𝟐 + (−𝟐𝟐)
= 𝟐𝟓 = 𝟓
Example 2: 𝒗 =
𝟐
𝟏𝟕
, −
𝟐
𝟏𝟕
,
𝟑
𝟏𝟕
𝒗 =
𝟐
𝟏𝟕
𝟐
+ −
𝟐
𝟏𝟕
𝟐
+
𝟑
𝟏𝟕
𝟐
=
𝟏𝟕
𝟏𝟕
= 𝟏 (𝑼𝒏𝒊𝒕 𝑽𝒆𝒄𝒕𝒐𝒓)

17. THE EUCLIDEAN
PLANE 𝐸2
MATH 208 – MODERN GEOM

18. At the end of the lesson the students will be able to:
 Define Euclidean plane.
 Solve the distance between two vectors.
OBJECTIVES

19. THE EUCLIDEAN PLANE 𝑬𝟐
The plane has both algebraic and geometric
aspects. The algebraic properties focuses on
the vector properties of 𝑅2.
In the geometric properties we will focus on the
concept of Distance.

20. THE EUCLIDEAN PLANE 𝑬𝟐
If P and Q are points, we define the
distance between P and Q by the equation:
d(P, Q) = |𝑸 − 𝑷|
The symbol 𝑬𝟐
will be used to denote the
set of points in Euclidean plane equipped
with the distance function d.

21. d(P, Q)=|Q-P|

22. THE EUCLIDEAN PLANE 𝑬𝟐
𝒅 𝑷, 𝑸 = |𝑸 − 𝑷|
Most important properties of the distance:
Theorem 5. let P, Q and R be points of 𝑬𝟐, 𝒕𝒉𝒆𝒏
i. d(P,Q)≥ 𝟎
ii. d(P,Q)=0 if and only if P=Q
iii. d(P,Q)=d(Q,P)
iv. d(P,Q)+d(Q,R)≥ 𝒅(𝑷, 𝑹)

23. d(P, Q)=|Q-P|
LET
1. P(3, 7) Q(-1, 4)
2. P(1, 2) Q(1, 2)

24. d(P, Q)=|Q-P|
LET d(Q, R)=|R-Q| d(P, R)=|R-P|
1. P(1, 5) Q(-2.1) R(3,-2)

25. LETd(P, Q)=|Q-P| d(Q, P)=|P-Q|
1. P(5,-3) Q(-2,4)

26. 𝑳𝑬𝑵𝑮𝑻𝑯 𝑰𝑵 𝑹𝒏
Seatwork: Answer the Following:
1. v= (3, -1, 0)
2. v=(0,1,2,3)

27. ASSESSMENT
Answer the following:
A.
Given: u= (2, -2) v=(5,8) w=(-4, 3)
1. <u, v>
2. ||𝒗||
3. <u, v+w>
B. Find the of the vector

28. ASSIGNMENT

29. Thank You!