The document discusses abstract data types (ADTs) and describes an array ADT. It lists common array operations like display, add, insert, delete, search, get, set, max, min, reverse, shift, and provides pseudocode implementations. Operations like insert and delete are O(n) linear time due to array element shifting. Search operations can be improved to O(1) constant time using techniques like transposition and move to front. Binary search provides O(logn) time complexity for sorted arrays. The document also discusses sorting an array, checking if an array is sorted, arranging negative numbers to the left, and merging two sorted arrays.

1. ADT(Abstract Data type) :- It represent the data and
set of operation on data.
Data:-
1. Array Space
2. Size
3. Length
Operation:-
1. Display()
2. Add(x)/append(x)
3. Insert(index x)
4. Delete(index)
5. Search(x)
6. Get(index)
7. Set(index x)
8. Max()/Min()
9. Reverse()
10. Shift()/rotate

2. 2. Add(x)/append(x):-
8 3 7 12 6 9 10
A
0 1 2 3 4 5 6 7 8 9
Size = 10
Length = 6 7
A[length] = x;
Length ++;
f(n) = 2
f(n) = 2no
O(no) = O(1)

3. 2. insert:-
8 3 7 12 6 9 10
A
0 1 2 3 4 5 6 7 8 9
Insert(4,15)
8 3 7 12 6 9 10
A
0 1 2 3 4 5 6 7 8 9
15
8 3 7 12 15 6 9 10
A
0 1 2 3 4 5 6 7 8 9
After Insertion

4. 4. Delete(index) :-
8 3 7 15 6 9 10
A
0 1 2 3 4 5 6 7 8 9
8 3 7 15 6 9 10
A
0 1 2 3 4 5 6 7 8 9
Delete(3);
8 3 7 6 9 10
A
0 1 2 3 4 5 6 7 8 9

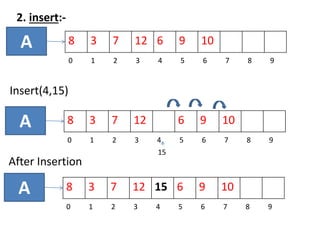
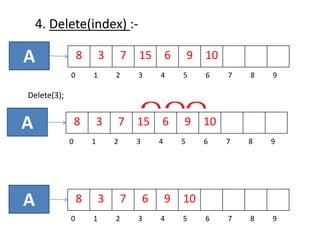
5. 4. Delete(index) :-
Code:-
x = A[index];
If(index>=0 && index<length)
{
for(i=index ;i<length-1 ;i++)
{
A[i] = A[i+1];
}
length--;
}

6. 4. Delete(index) :-
Linear search:-
• Start from the leftmost element of arr[] and one by
one compare x with each element of arr[]
• If x matches with an element, return the index.
• If x doesn’t match with any of elements, return -1.
• Time complexity is O(n).

7. Improve linear search:-
A linear search or sequential search is a method for finding an
element within a list. It sequentially checks each element of
the list until a match is found or the whole list has been
searched. It is observed that when searching for a key
element, then there is a possibility for searching the same
key element again and again.
The goal is that if the same element is searched again then
the operation must take lesser time. Therefore, in such a
case, Linear Search can be improved by using the following
two methods:
1. Transposition
2. Move to Front

8. Transposition:
In transposition, if the key element is found, it is swapped to the
element an index before to increase in a number of search count for
a particular key, the search operation also optimizes and keep
moving the element to the starting of the array where the searching
time complexity would be of constant time.
For Example: If the array arr[] is {2, 5, 7, 1, 6, 4, 5, 8, 3, 7} and let
the key to be searched is 4, then below are the steps:
• After searching for key 4, the element is found at index 5 of the given array
after 6 comparisons. Now after transposition, the array becomes {2, 5, 7, 1, 4,
6, 5, 8, 3, 7} i.e., the key with value 4 comes at index 4.
• Again after searching for key 4, the element is found at index 4 of the given
array after 6 comparisons. Now after transposition, the array becomes {2, 5, 7,
4, 1, 6, 5, 8, 3, 7} i.e., the key with value 4 comes at index 3.
• The above process will continue until any key reaches the front of the array if
the element to be found is not at the first index

9. Move to Front/Head:
In this method, if the key element is found then it is directly swapped with the
index 0, so that the next consecutive time, search operation for the same key
element is of O(1), i.e., constant time.
For Example: If the array arr[] is {2, 5, 7, 1, 6, 4, 5, 8, 3, 7} and let the key to be
searched is 4, then below are the steps:
• After searching for key 4, the element is found at index 5 of the
given array after 6 comparisons. Now after moving to front
operation, the array becomes {4, 2, 5, 7, 1, 6, 5, 8, 3, 7} i.e., the
key with value 4 comes at index 0.
• Again after searching for key 4, the element is found at index 0 of
the given array which reduces the entire’s search space.

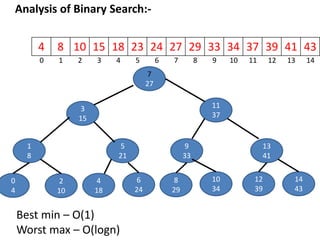
10. 4 8 10 15 18 23 24 27 29 33 34 37 39 41 43
Binary search :-
Size =15
Length = 15
key = 18
L H mid=[(L+H)/2]
0 14 7
0 6 3
4 6 5
4 4 4(found)
key = 34
L H mid
0 14 7
8 14 11
8 10 9
10 10 10(found)
key = 25
L H mid
0 14 7
0 6 3
4 6 5
6 6 6
7 6 X(not found)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

11. Binary Search algorithm:-
Algorithm BiSearch(l,h,key)
{
while(l<=h)
{
mid = [(l+h)/2];
if(key == A[mid])
return mid;
else if(key < A[mid])
h = mid-1;
else
l = mid + 1;
}
return -1;
}

12. Binary search Algorithm using recursion:-
Algorithm RBinSearch(l,h,key)
{
if(l <= h)
{
mid = [(l+h)/2];
if(key == A[mid])
return mid;
else if(key < A[mid])
return RBSearch(l,mid-1,key);
else
return RBSearch(mid+1,h,key)
}
return -1;
}

13. Analysis of Binary Search:-
4 8 10 15 18 23 24 27 29 33 34 37 39 41 43
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
7
27
3
15
11
37
1
8
5
21
9
33
13
41
0
4
2
10
4
18
6
24
8
29
10
34
12
39
14
43
Best min – O(1)
Worst max – O(logn)

14. 6. get(index):- to get the element of given index
get(index)
{
if(index >=0 && index<length)
return A[index];
}
7. set(index):- to set the value of element of given index
set(index,x)
{
if(index >=0 && index<length)
A[index] = x;
}

15. 8. max() & min():-
max()
{
1-------max = A[0];
n-------for(i=1;i<length;i++)
{
n-1 ---------if(A[i]>max)
1-----------------max = A[i];
}
return max;
}
f(n) = 2n+1
O(n)
min()
{
1-------min = A[0];
N-------for(i=1;i<length;i++)
{
n-1 ----------if(A[i]<min)
1-----------------min = A[i];
}
return min;
}
f(n) = 2n+1
O(n)

16. Sum():-
Sum()
{
total = 0;
for(i=0;i<length;i++)
{
total = total + A[i];
}
return total;
}
avg():-
Sum()
{
total = 0;
for(i=0;i<length;i++)
{
total = total + A[i];
}
return total/n ;
}

17. 9. reverse()
8 3 7 15 6 9 10 2 12 4
0 1 2 3 4 5 6 7 8 9
A
4 12 2 10 9 6 15 7 3 8
0 1 2 3 4 5 6 7 8 9
B
reverse
4 12 2 10 9 6 15 7 3 8
0 1 2 3 4 5 6 7 8 9
A
for(i=length-1,j=0;i>=0;i--,j++)
{
B[j] = A[i];---------------n
}
for(i=0;i<length;i++)
{
A[i] = B[i];---------------n
} 2n O(n)

18. 9. reverse()
8 3 7 15 6 9 10 2 12 4
0 1 2 3 4 5 6 7 8 9
A
4 12 2 10 9 6 15 7 3 8
0 1 2 3 4 5 6 7 8 9
A
for(i=0,j=length-1;i<j;i++,j--)
{
temp = A[i];
A[i] = A[j];
A[j] = temp;
}

19. 10. shift/rotate:-
8 3 7 15 6
0 1 2 3 4
A
3 7 15 6 0
0 1 2 3 4
A
8
Left shift
8 3 7 15 6
0 1 2 3 4
A
0 8 3 7 15
0 1 2 3 4
A 8 Right shift

20. 8 3 7 15 6
0 1 2 3 4
A
Rotate:-
3 7 15 6 8
0 1 2 3 4
A

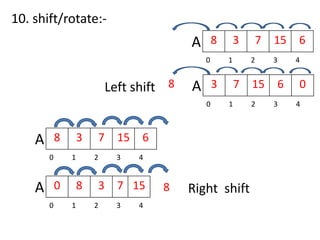
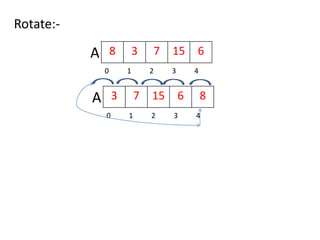
21. Insert An element in sorted array :-
4 8 13 16 20 25 28 33
0 1 2 3 4 5 6 7 8 9
A
Insert – 18
x = 18;
I = length-1;
while(A[i]>x)
{
A[i+1] = A[i];
}
A[i+1] = x;

22. Array is sorted or not :-
4 8 13 26 20 25 28 33
0 1 2 3 4 5 6 7 8 9
A
Algorithm isSorted(A,n)
{
for(i=0;i<n-1;i++)
{
if(A[i]>A[i+1])
return false;
}
return true;
}

23. Arrange –ve number on Left side:-
-6 3 -8 10 5 -7 -9 12 -4 2
0 1 2 3 4 5 6 7 8 9
A
i=0;
j = length-1;
While(i<j)
{
while(A[i]<0){i++;}
while(A[i]>=0){i++;}
if(i<j)
swap(A[i],A[j]);
}
-6 -4 -8 -9 -7 5 10 12 3 2
0 1 2 3 4 5 6 7 8 9
A

24. merging:-
Merging can be done only on sorted array.
In merging we have combine two sorted array and combine them to make a single
sorted array.
2 4 6 8 10
0 1 2 3 4
A
3 5 7 9 11
0 1 2 3 4
B
2 3 4 5 6 7 8 9 10 11
0 1 2 3 4 5 6 7 8 9
C
After merging:-