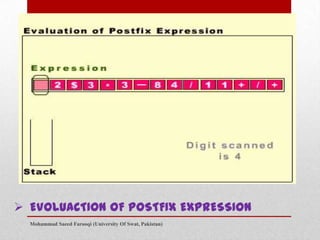
Mohammad Saeed Farooqi presented on data structures and algorithms. He discussed infix, postfix, and prefix notation, operator precedence, evaluating postfix expressions using stacks, and converting infix to postfix using stacks. He provided examples and algorithms for postfix expression evaluation and converting between infix, postfix, and prefix notation.

1. PRESENTATION
OF
DATA STRUCTURE & ALGORITHM
BY
Mohammad Saeed Farooqi

2.  INFIX Notation.
 POSTFIX Notation.
 PREFIX Notation.
 OPERATORS PRECEDENCE.
 Evaluating Of POSTFIX Expression Using Stacks.
 Converting INFIX To POSTFIX Using Stacks.
 ALGORITHMS.

OUTLINES
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

3.  Infix Expression Are Those In Which Operators Are
Written Between Two Operands.
 Infix Expression Is The Common Arithmetic And
Logical Formula Expression.
 Infix Expression Needs Extra Information To Make The
Order Of Evaluation Of The Operators Clear.
 Rules Built Into The Language About Operator
Precedence And Associativity, And Brackets ( ) To Allow
Users To Override These Rules.
 INFIX EXPRESSION
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

4.  EXAMPLE…
 A * ( B + C ) / D…
 This Expression Is Usually Taken To Mean Something
Like: "First Add B And C Together, Then Multiply The
Result By A, Then Divide By D To Give The Final
Answer.
 INFIX EXPRESSION
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

5.  POSTFIX Expression Also Known As “Reverse Polish
Expression”
 In These Expressions Operators Are Written After Their
Operands.
 Operators Act On Values Immediately To The Left Of
Them.
 They Do Not Have (Brackets)
 POSTFIX EXPRESSION
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

6.  EXAMPLE…
 A B C + * D /…
 Operators Act On Values Immediately To The Left Of
Them.
 For Example, The "+" Above Uses The "B" And "C".
 We Can Add (Totally Unnecessary) Brackets To Make
This Easy.
( (A (B C +) *) D /) .
 POSTFIX EXPRESSION
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

7.  Also Known As “Polish Expression”.
 In These Expressions Operators Are Written Before The
Operands.
 We Have To Scan It From Right-To-Left.
 As For Postfix, Operators Are Evaluated Left-To-Right And
Brackets Are Superfluous.
 Operators Act On The Two Nearest Values On The Right.
 I Have Again Added (Totally Unnecessary) Brackets To Make
This Clear.
(/ (* A (+ B C) ) D)
 PREFIX Notation Is Especially Popular With StackBased Operations Due To Its Innate Ability To Easily
Distinguish Order Of Operations Without The Need For
Parentheses.
 PREFIX EXPRESSION
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

8.  We Assume The Following Three Levels Of
PRECEDENCE For The Usual Five Binary Operations.
 Highest
Exponentiation ().
 Next Highest Multiplication (*) And Division (/)
Superfluous
 Lowest
Addition (+) And Subtraction (-)
 Without Understanding Operator Precedence You Can
Not Convert Any Expression.
 OPERATOR PRECEDENCE
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

9.  EVOLUACTION OF POSTFIX EXPRESSION
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

10. • EvaluatePostfix(exp)
• {
• Create A Stack S.
• for I ← 0 to length of the (exp)-1
{
if(exp[i]) // Is An Operand
push(exp[i]);
else if(exp[i])
// Is An Operator
{
op1←pop();
op2← pop();
result←perform(exp[i],op1,op2);
push(result);
}
}
}
 ALGORITHM FOR POSTFIX EVALUATION
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

11. Converting Infix To Postfix
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

12. •
•
•
•
•
•
•
Example: 1*2+3.
Scan: *,+ (Stack) And 12 (Postfix Expression).
Precedence Of * Is Higher Than +.
Thus, Append * to postfix Expression.
+ (Stack) And 12* (Postfix Expression ).
Scan Further, + (Stack ) and 12*3 (Postfix Expression)
There Are No Further Operators, Thus, Postfix Is 12*3+
Converting Infix To Postfix
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

13. Converting Infix To Prefix
Mohammad Saeed Farooqi (University Of Swat, Pakistan)

14. • Step 1. Push “)” onto STACK, and add “(“ to end of the A.
• Step 2. Scan A from right to left and repeat step 3 to 6 for each element of A
until the STACK is empty.
• Step 3. If an operand is encountered add it to B.
• Step 4. If a right parenthesis is encountered push it onto STACK.
• Step 5. If an operator is encountered then: a. Repeatedly pop from STACK
and add to B each operator (on the top of STACK) which has same or higher
precedence than the operator. b. Add operator to STACK.
• Step 6. If left parenthesis is encontered then a. Repeatedly pop from the
STACK and add to B (each operator on top of stack until a left parenthesis is
encounterd) b. Remove the left parenthesis.
• Step 7. Exit
Converting Infix To Postfix
Mohammad Saeed Farooqi (University Of Swat, Pakistan)