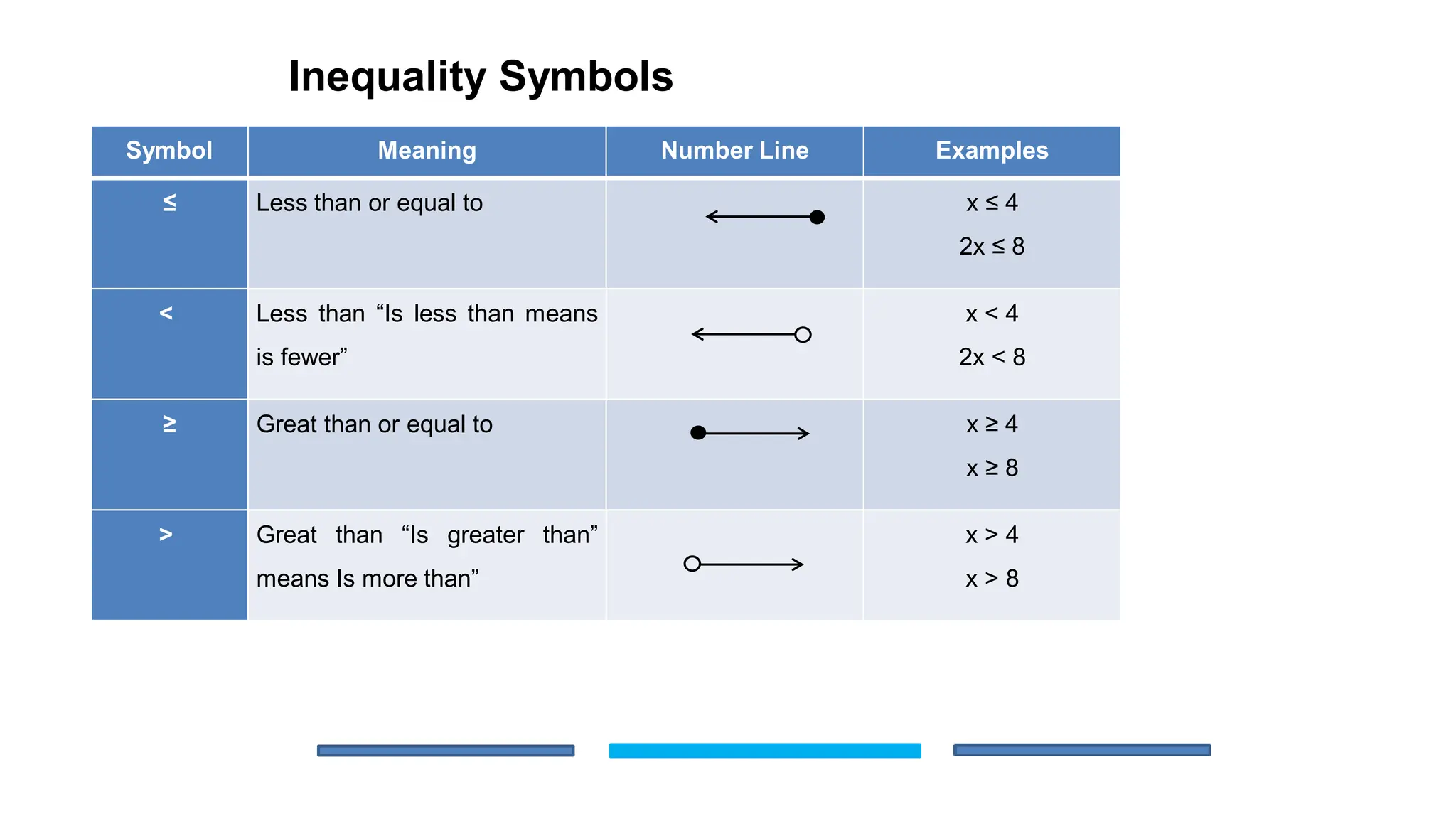
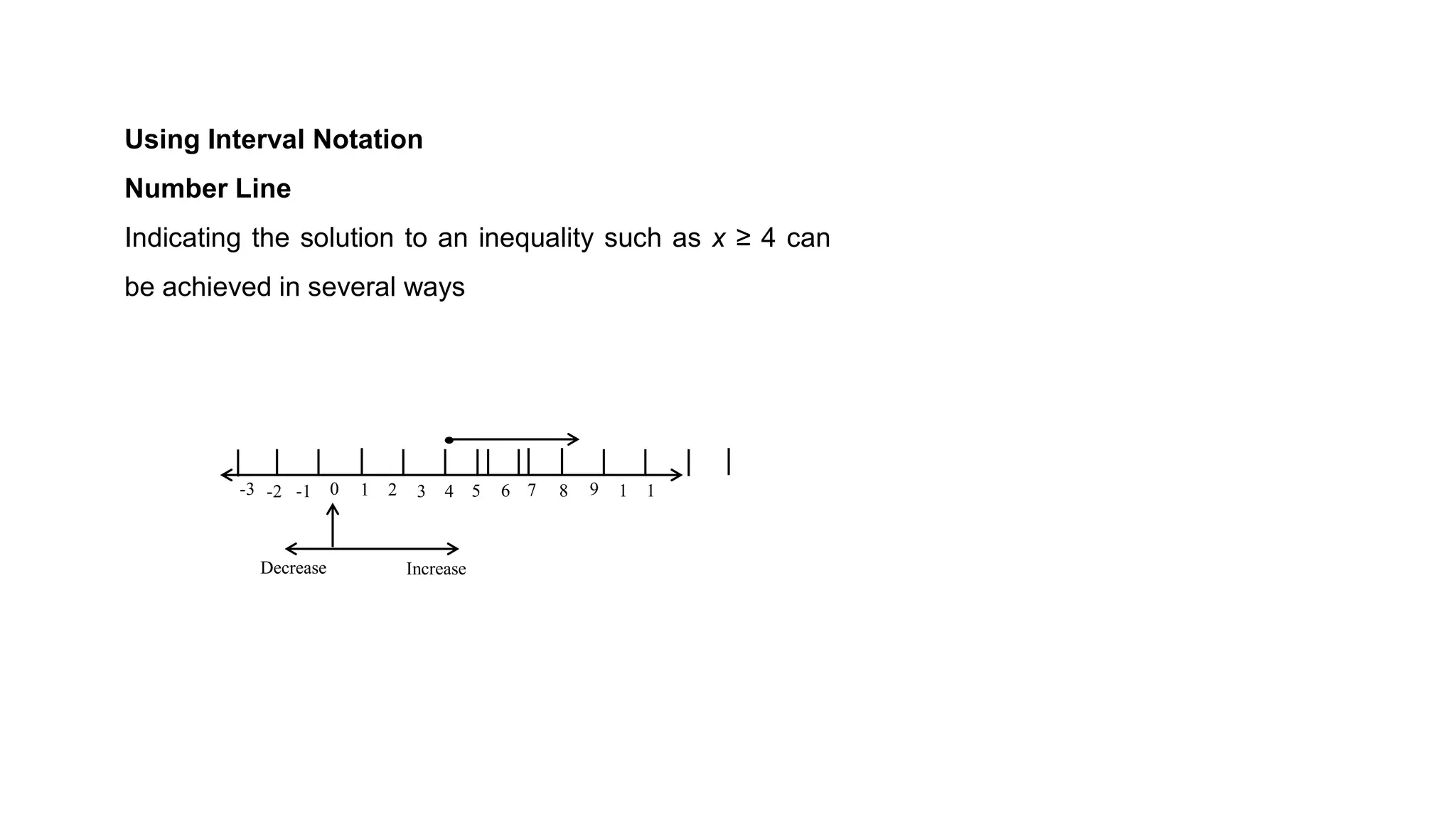
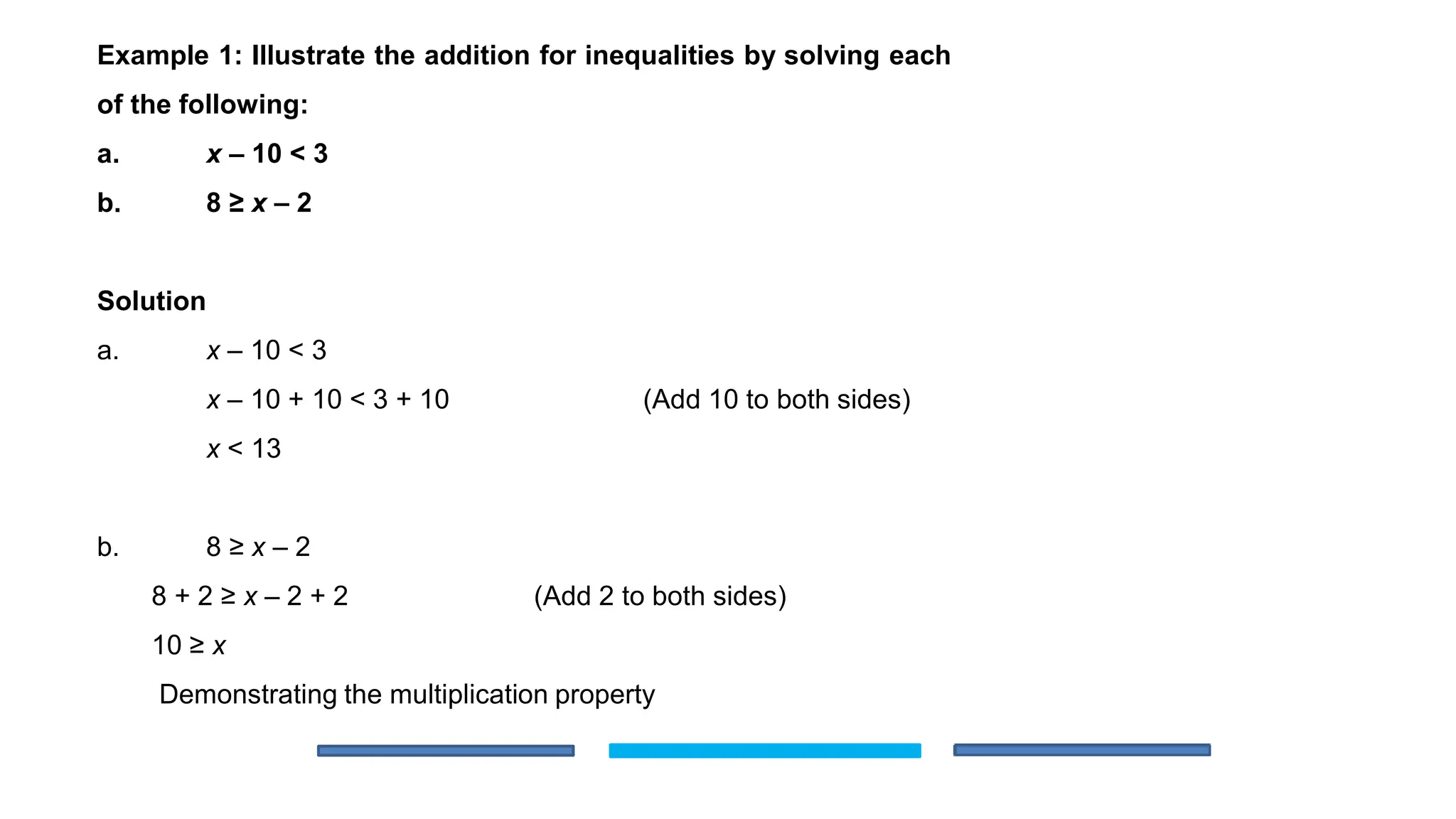
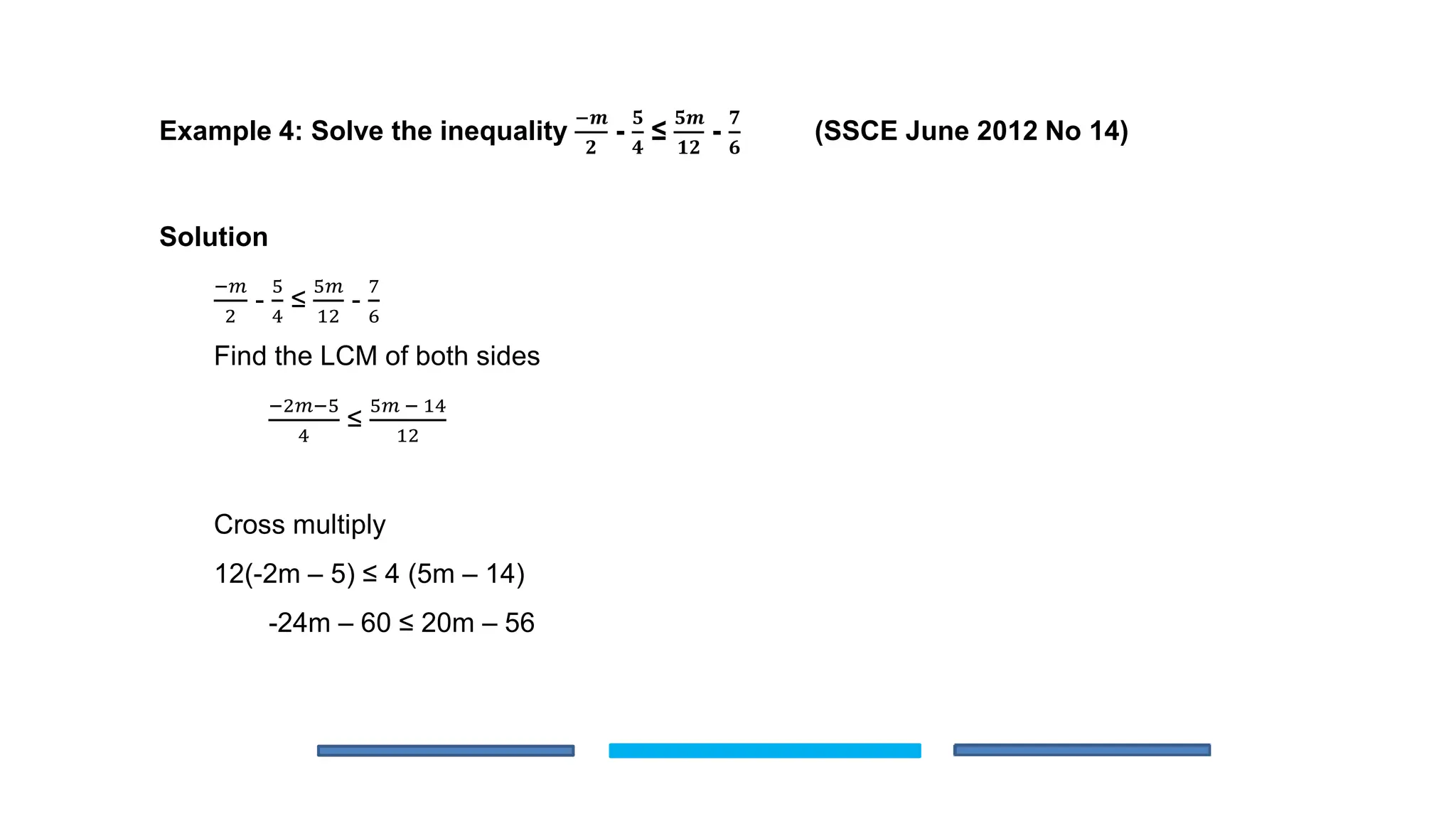
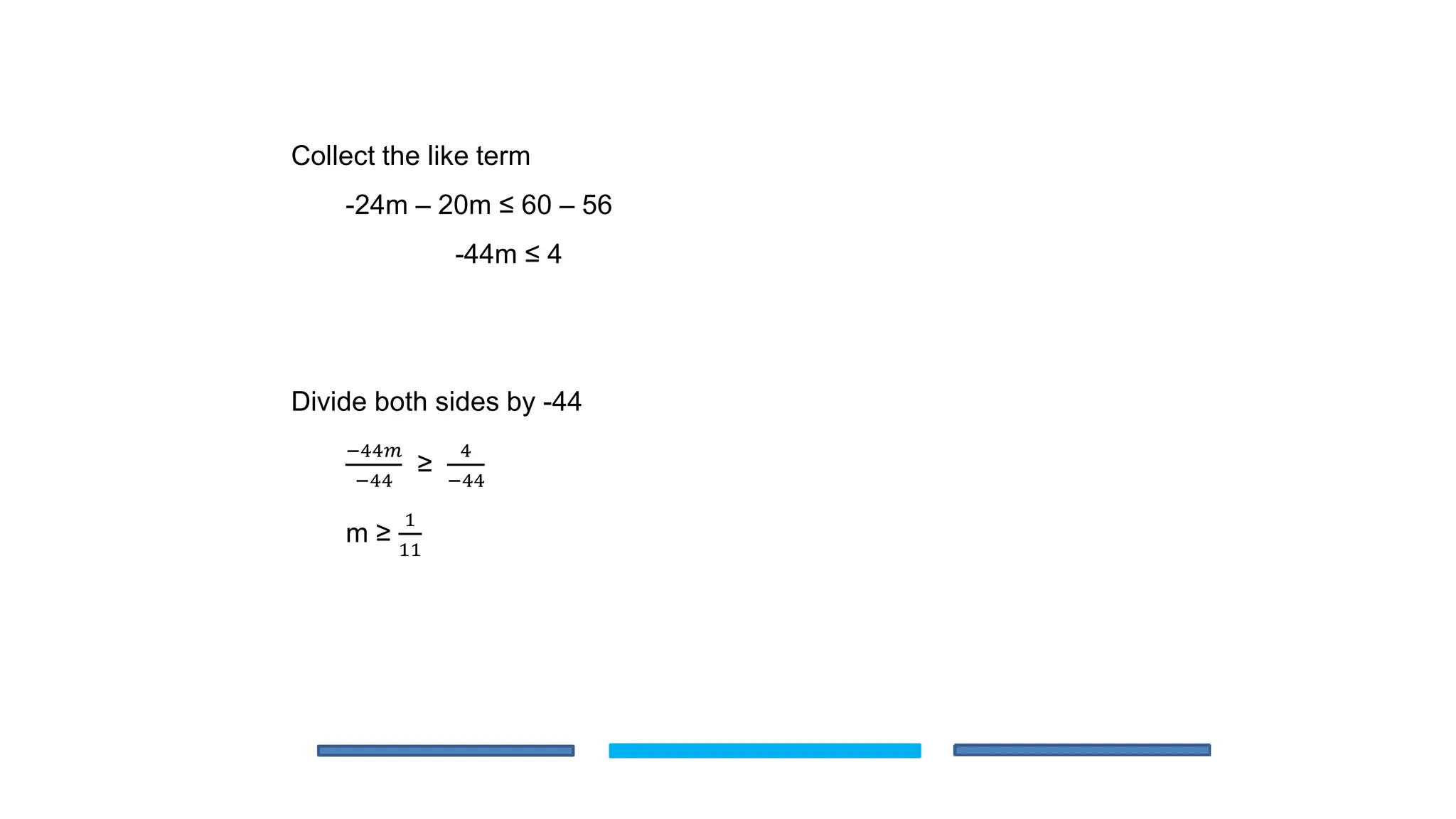
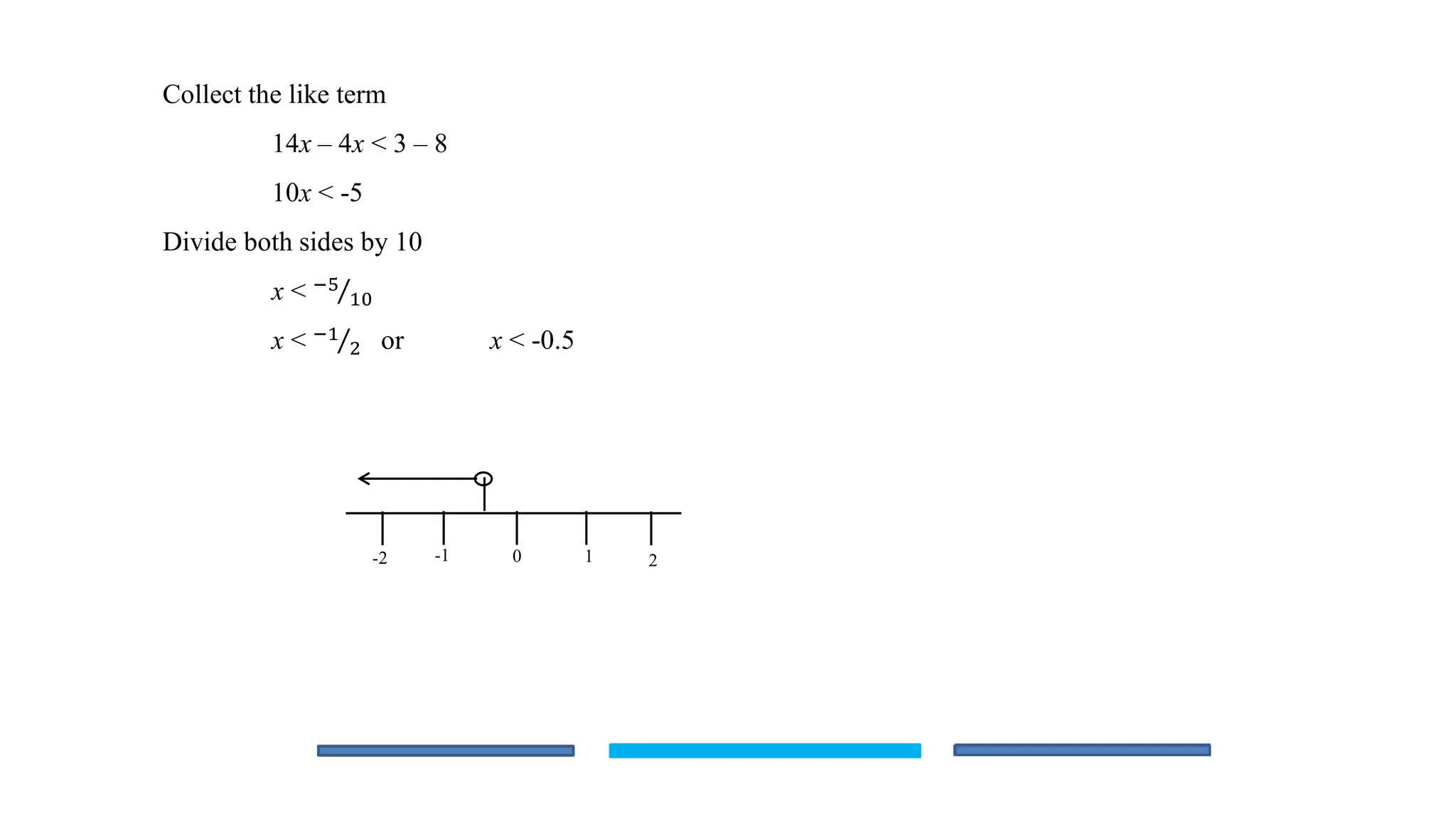
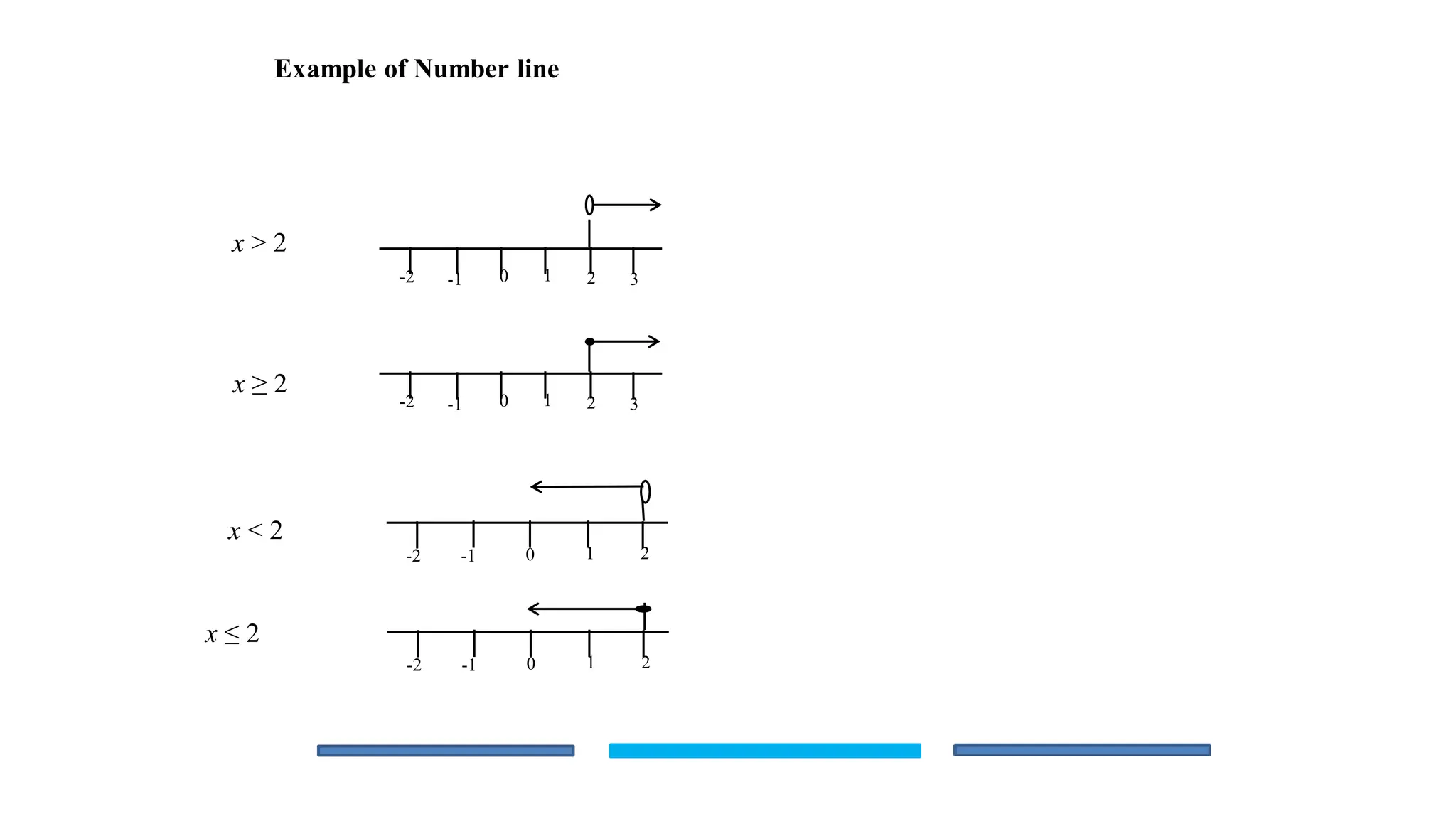
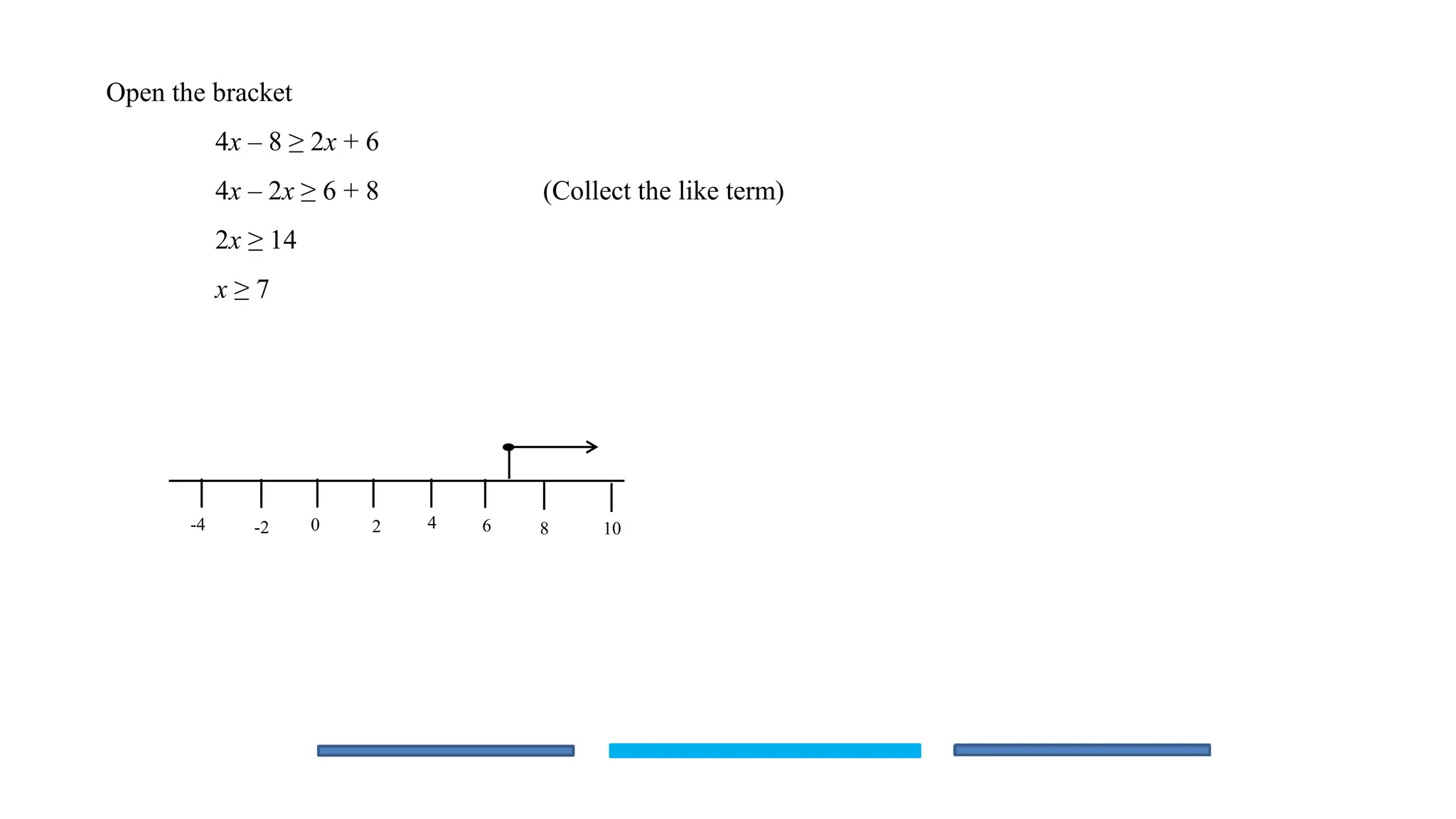
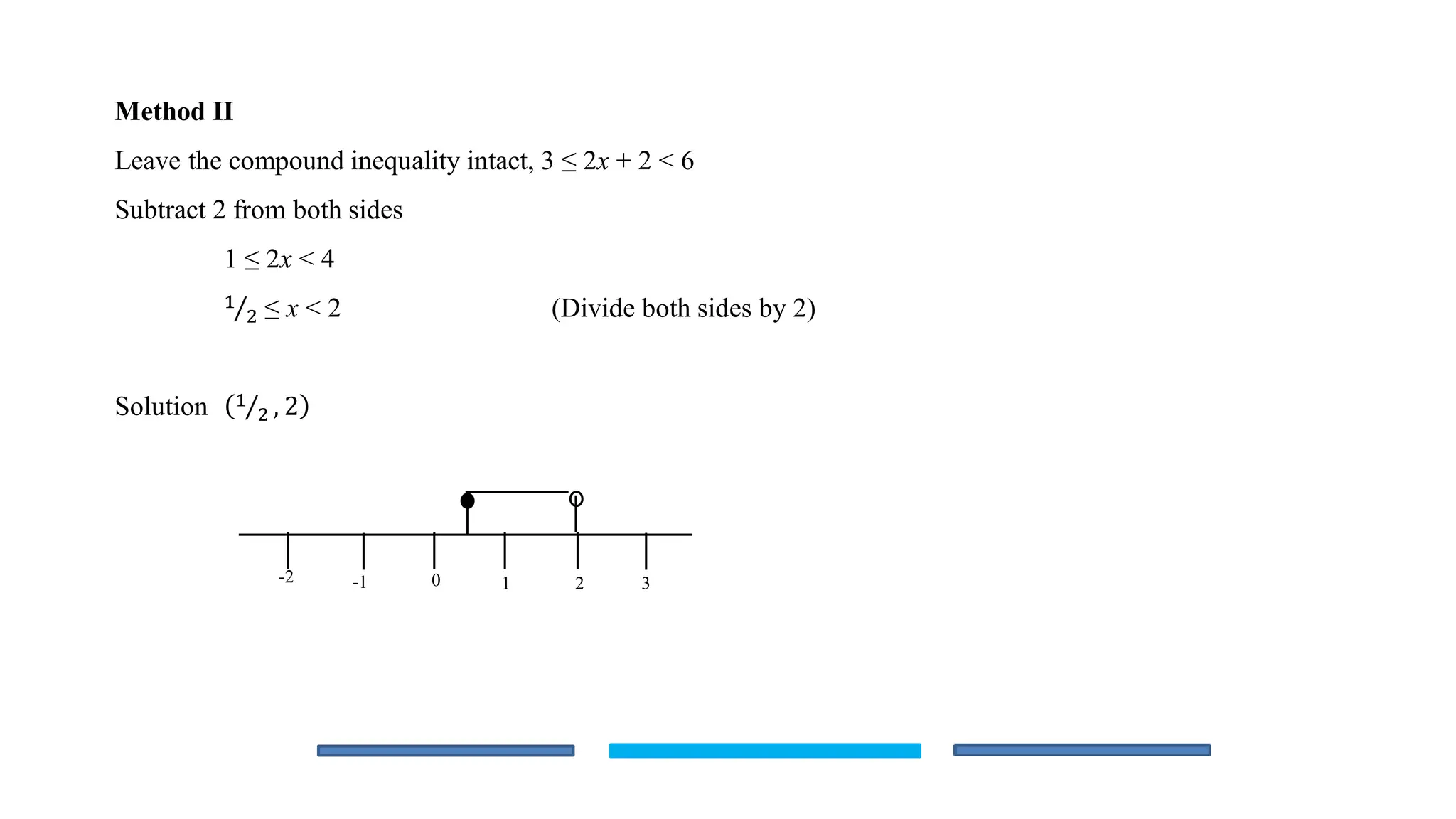
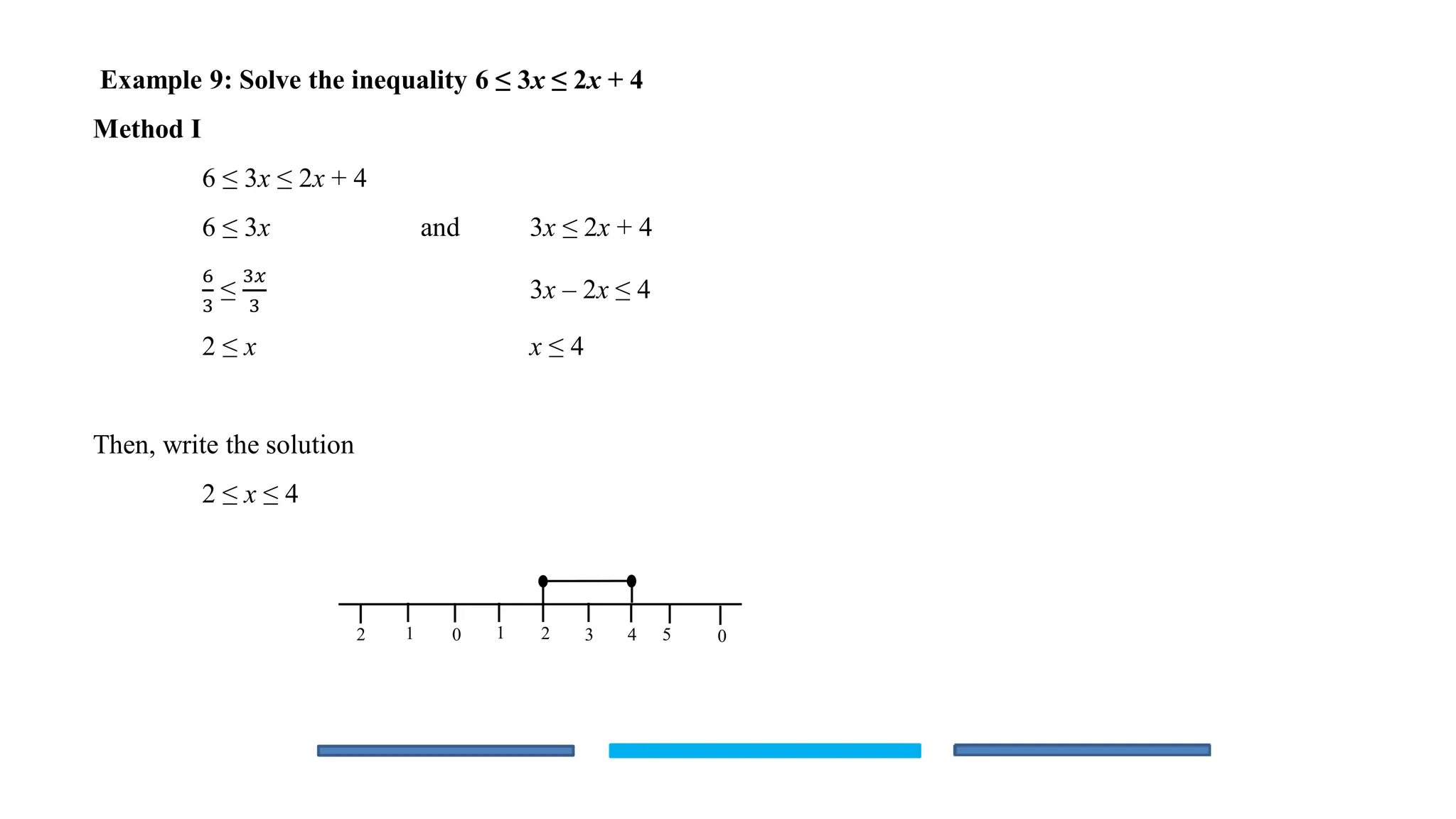
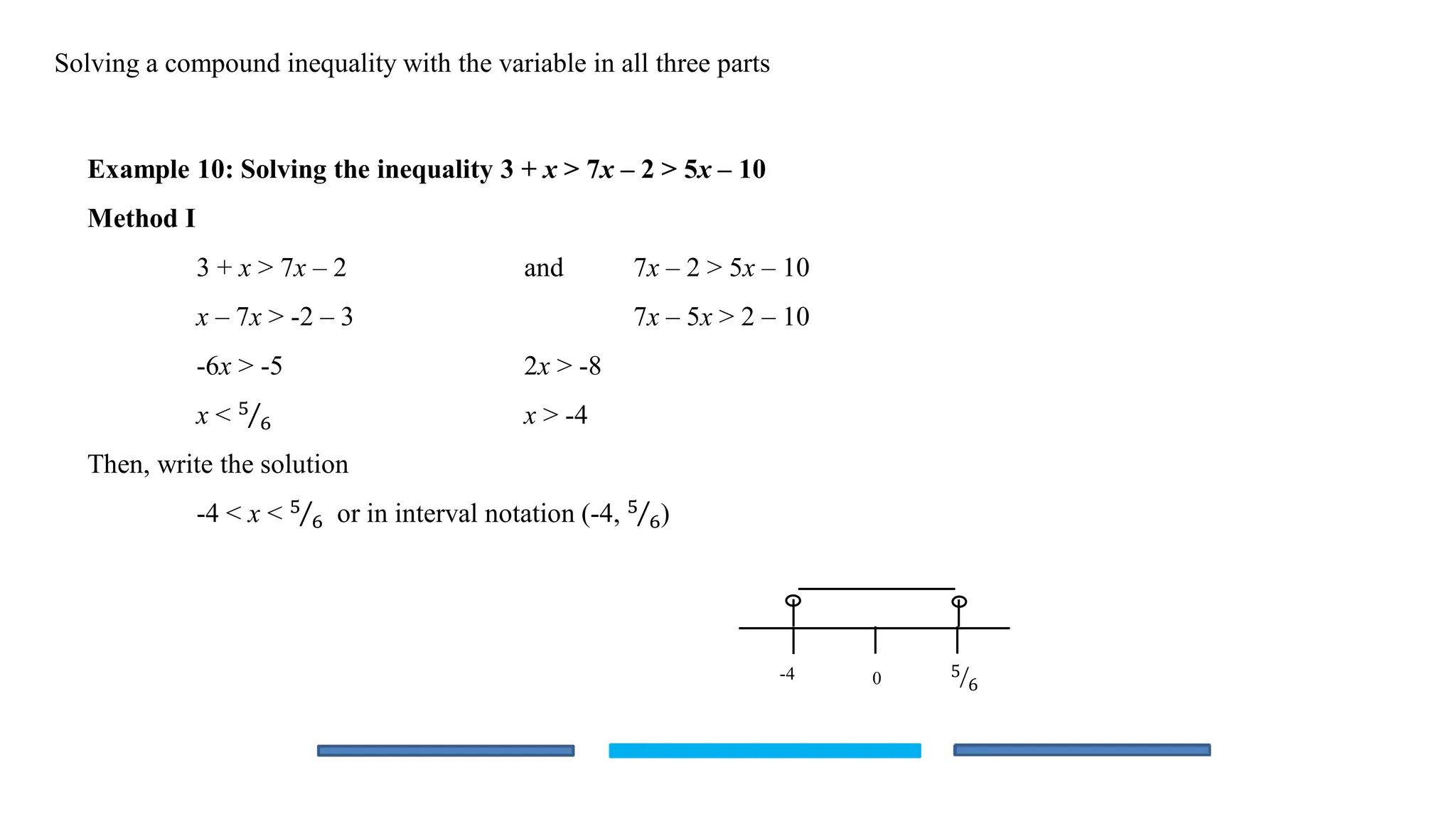
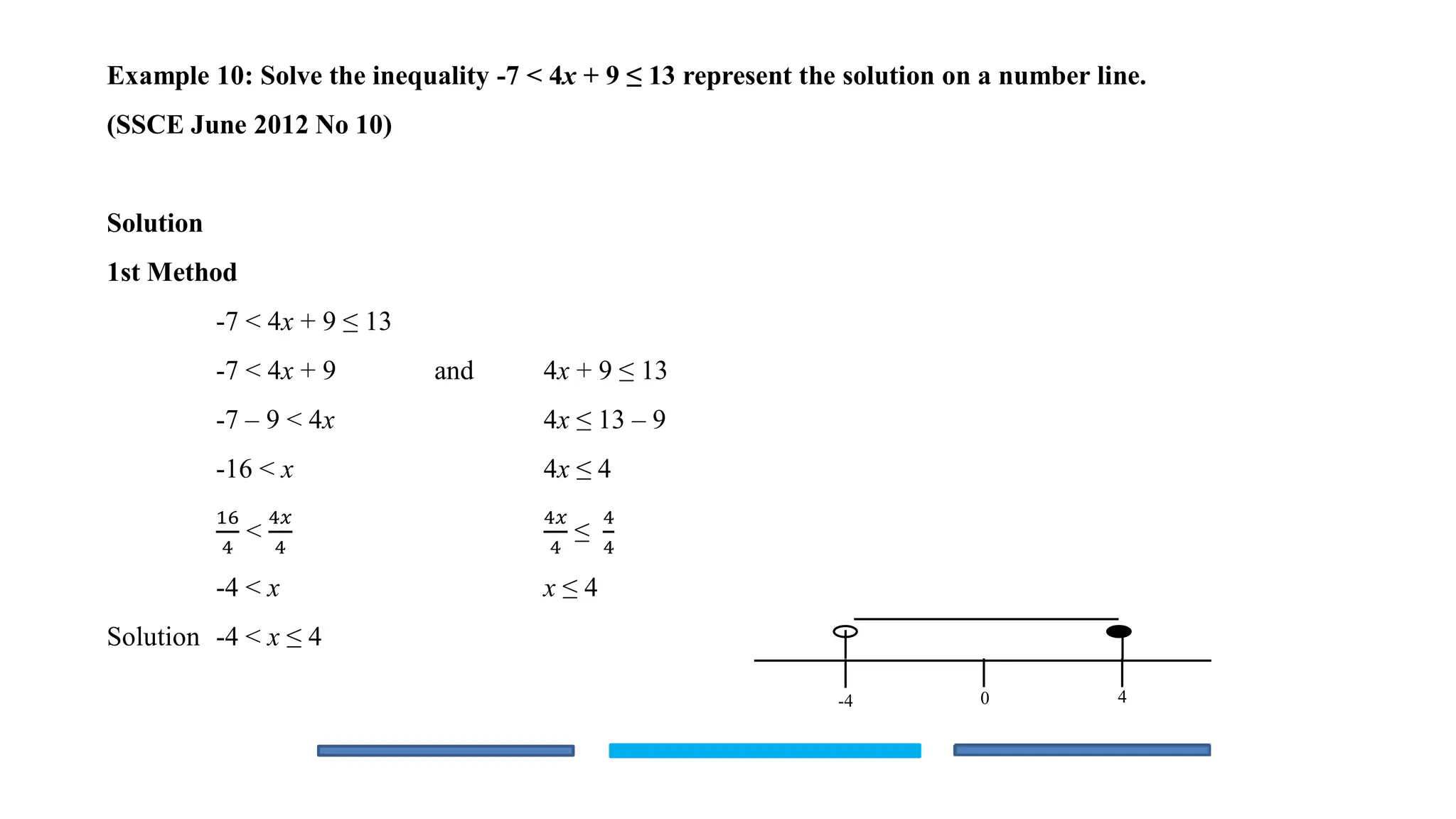
The document is an educational lesson focused on linear inequalities in mathematics, including how to represent and solve inequalities in one variable. It covers key concepts such as inequality symbols, properties of inequalities, and methods for solving both simple and compound inequalities, with examples and solutions provided for clarity. Additionally, it includes guidance on representing solutions on number lines.

1. CLASS
TOPIC
SS2
LINEAR INEQUALITIES
SUBJECT
MATHEMATICS

2. LESSON OBJECTIVE
At the end of this session you should be able to:
1. Represent inequalities in one variable on a number line
2. Solve inequalities in one variable
3. Combine two inequalities to form compound inequalities

3. LINEAR INEQUALITIES

4. Symbol Meaning Number Line Examples
≤ Less than or equal to x ≤ 4
2x ≤ 8
< Less than “Is less than means
is fewer”
x < 4
2x < 8
≥ Great than or equal to x ≥ 4
x ≥ 8
> Great than “Is greater than”
means Is more than”
x > 4
x > 8
Inequality Symbols

5. Using Interval Notation
Number Line
Indicating the solution to an inequality such as x ≥ 4 can
be achieved in several ways
5 6 7 8 9 1 1
-2 -1 0 1 2 3 4
-3
Decrease Increase

6. b. Multiplication property
If a < b and c > o, then ac < bc
If a < b and c < o, then ac > bc
These properties also apply to a ≤ b, a > b and a ≥ b
Demonstrating the addition property
Using the Properties of Inequalities
a. Addition property
if a < b, then a + c < b + c

7. Example 1: Illustrate the addition for inequalities by solving each
of the following:
a. x – 10 < 3
b. 8 ≥ x – 2
Solution
a. x – 10 < 3
x – 10 + 10 < 3 + 10 (Add 10 to both sides)
x < 13
b. 8 ≥ x – 2
8 + 2 ≥ x – 2 + 2 (Add 2 to both sides)
10 ≥ x
Demonstrating the multiplication property

8. Example 2: Illustrate the multiplication property for
inequalities by each of the following:
a. 2x < 10
b. -3x – 2 > 7
Solution
a. 2x < 10
2x < 10
1
2
(2x) <
1
2
(10) (Multiply both sides by ½)
x < 5

9. b. -3x – 2 > 7
-3x – 2 + 2 > 7 + 2 (Add 2 to both sides)
-3x > 9
-
1
3
(-3x) < -
1
3
(9) (Multiply both sides by 1/3)
x < -3 (Reverse the inequalities)

10. Solving Inequalities in One Variable Algebraically
Example 3: Solve the inequality 1 – 2x < - 1/3 (SSCE June 2008 No 41)
Solution
1 – 2x < - 1/3
Multiply both sides by 3
3(1 – 2x) < -1/3 x 3
3 – 6x < -1
Subtract 3 from both sides
-6x < -4
Divide both sides by -6
−6𝑥
−6
> Τ
−4
−6
x > Τ
2
3

11. Example 4: Solve the inequality
−𝒎
𝟐
-
𝟓
𝟒
≤
𝟓𝒎
𝟏𝟐
-
𝟕
𝟔
(SSCE June 2012 No 14)
Solution
−𝑚
2
-
5
4
≤
5𝑚
12
-
7
6
Find the LCM of both sides
−2𝑚−5
4
≤
5𝑚 − 14
12
Cross multiply
12(-2m – 5) ≤ 4 (5m – 14)
-24m – 60 ≤ 20m – 56

12. Collect the like term
-24m – 20m ≤ 60 – 56
-44m ≤ 4
Divide both sides by -44
−44𝑚
−44
≥
4
−44
m ≥
1
11

13. Example 5: Solve the inequality:
𝟐𝒙 − 𝟓
𝟐
< (2 – x) (SSCE June 2013 No 10)
Solution
2𝑥 − 5
2
<
(2 – 𝑥)
1
Cross multiply
1(2x -5) < 2(2 – x)
2x – 5 < 4 – 2x
Collect the like term
2x + 2x < 4 + 5
4x < 9
x < Τ
9
4
x < 2 Τ
1
4

14. Example 6: Solve 7x + 4 <
𝟏
𝟐
(4x + 3) represent your answer in number
line. (SSCE 2013 theory No 2a)
Solution
7x + 4 <
1
2
(4x + 3)
Cross multiply
2(7x + 4) < 1(4x + 3)
14x + 8 < 4x + 3

15. Collect the like term
14x – 4x < 3 – 8
10x < -5
Divide both sides by 10
x < Τ
−5
10
x < Τ
−1
2 or x < -0.5
-2 -1 0 1 2

16. Example of Number line
-2 -1 0 1 2 3
x > 2
x ≥ 2
-2 -1 0 1 2 3
x < 2
-2 -1 0 1 2
x ≤ 2
-2 -1 0 1 2

17. Example 7: Solve the inequality
𝒙 − 𝟐
𝟐
≥
𝒙 + 𝟑
𝟒
, represent the solution of the inequality
on the number lines. (SSCE June 2006 No 14)
Solution
𝑥 − 2
2
≥
𝑥 + 3
4
Cross multiply
4(x – 2) ≥ 2(x + 3)
Open the bracket
4x – 8 ≥ 2x + 6
4x – 2x ≥ 6 + 8 (Collect the like term)
2x ≥ 14
x ≥ 7

18. -4 -2 0 2 4 6 8 10
Open the bracket
4x – 8 ≥ 2x + 6
4x – 2x ≥ 6 + 8 (Collect the like term)
2x ≥ 14
x ≥ 7

19. Understanding Compound Inequalities with Two Variables
A compound inequality includes two inequalities in one statement.
A statement such as 3 < x ≤ mean 3 < x and x ≤ 9. There are two
ways to solve compound inequalities. Separating them into two
separate inequalities or leaving the compound inequality intact and
performing operations on all three parts at the time. We will
illustrate both methods.

20. Example: Solve the compound inequality 3 ≤ 2x + 2 < 6
Method I
Separate the two inequalities
3 ≤ 2x + 2 and 2x + 2 < 6
Subtract 2 from both sides
1 ≤ 2x and 2x < 4
1
2
≤ x x < 2
Then, write the solution
1
2
≤ x < 2. Solution Τ
1
2 , 2

21. Method II
Leave the compound inequality intact, 3 ≤ 2x + 2 < 6
Subtract 2 from both sides
1 ≤ 2x < 4
Τ
1
2 ≤ x < 2 (Divide both sides by 2)
Solution Τ
1
2 , 2
-2 -1 0 1 2 3

22. Example 9: Solve the inequality 6 ≤ 3x ≤ 2x + 4
Method I
6 ≤ 3x ≤ 2x + 4
6 ≤ 3x and 3x ≤ 2x + 4
6
3
≤
3𝑥
3
3x – 2x ≤ 4
2 ≤ x x ≤ 4
Then, write the solution
2 ≤ x ≤ 4
1 0 1 2 3 4 5 0
2

23. Solving a compound inequality with the variable in all three parts
Example 10: Solving the inequality 3 + x > 7x – 2 > 5x – 10
Method I
3 + x > 7x – 2 and 7x – 2 > 5x – 10
x – 7x > -2 – 3 7x – 5x > 2 – 10
-6x > -5 2x > -8
x < Τ
5
6 x > -4
Then, write the solution
-4 < x < Τ
5
6 or in interval notation (-4, Τ
5
6)
-4 0 ൗ
5
6

24. Example 10: Solve the inequality -7 < 4x + 9 ≤ 13 represent the solution on a number line.
(SSCE June 2012 No 10)
Solution
1st Method
-7 < 4x + 9 ≤ 13
-7 < 4x + 9 and 4x + 9 ≤ 13
-7 – 9 < 4x 4x ≤ 13 – 9
-16 < x 4x ≤ 4
16
4
<
4𝑥
4
4𝑥
4
≤
4
4
-4 < x x ≤ 4
Solution -4 < x ≤ 4
-4 0 4

25. EVALUATIONS
1. Solve the inequality:
𝟑𝒙 − 𝟓
𝟐
< (2 + x)
2. Solve 5x – 3 <
𝟏
𝟐
(3x + 5) represent
your answer in number line.
3. Solve the compound inequality 5 ≤ 3x + 2 <
8