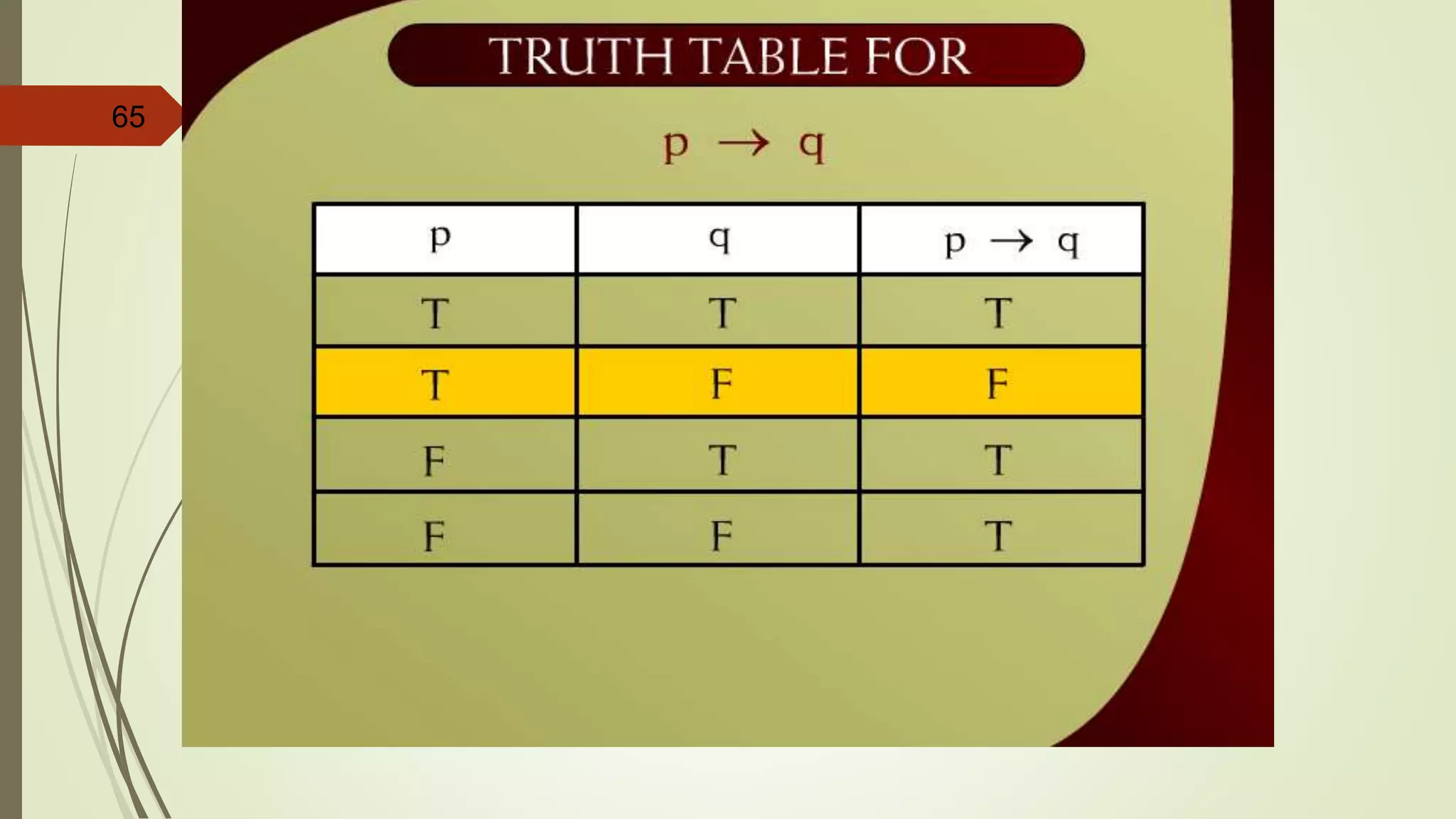
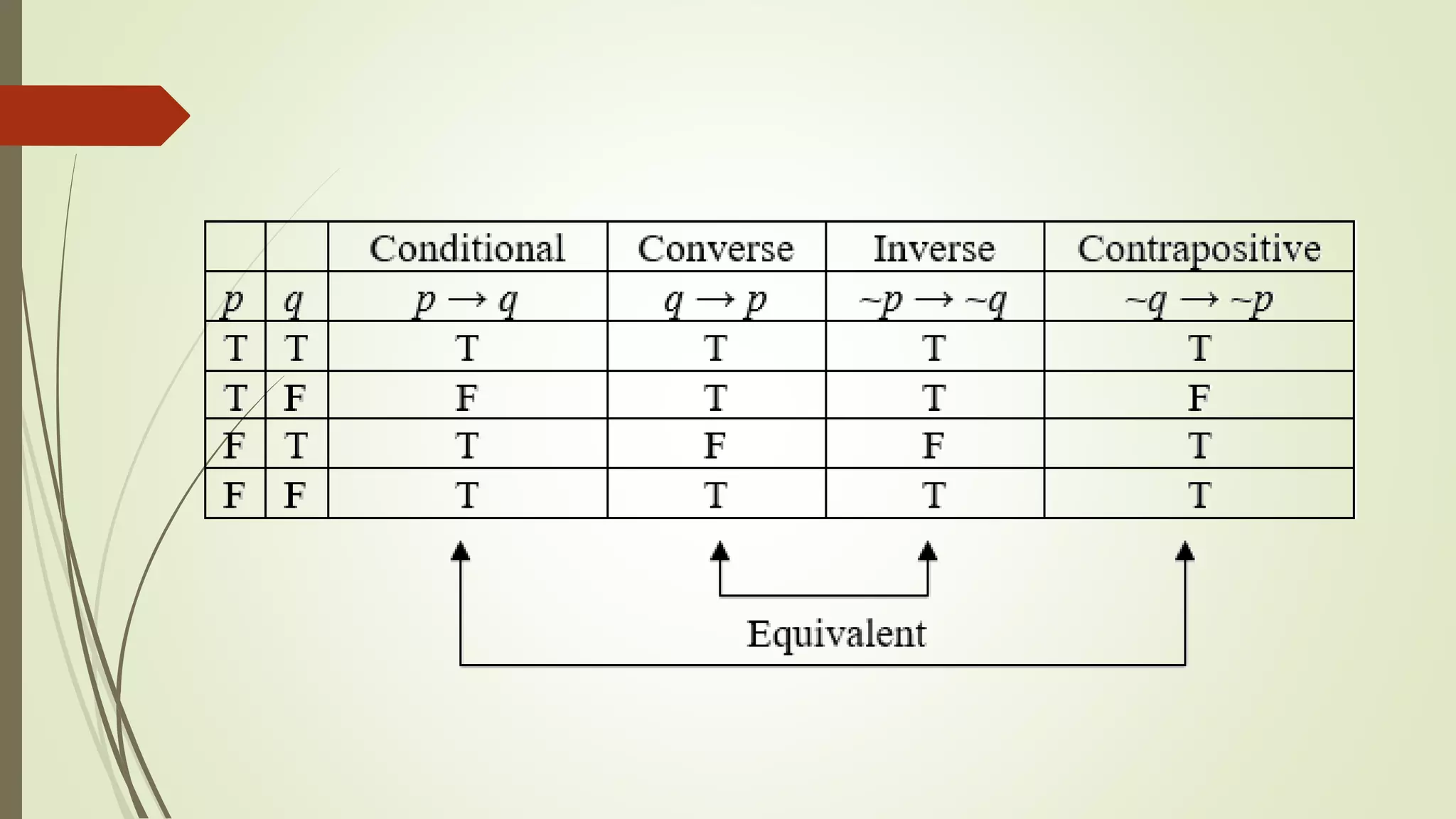
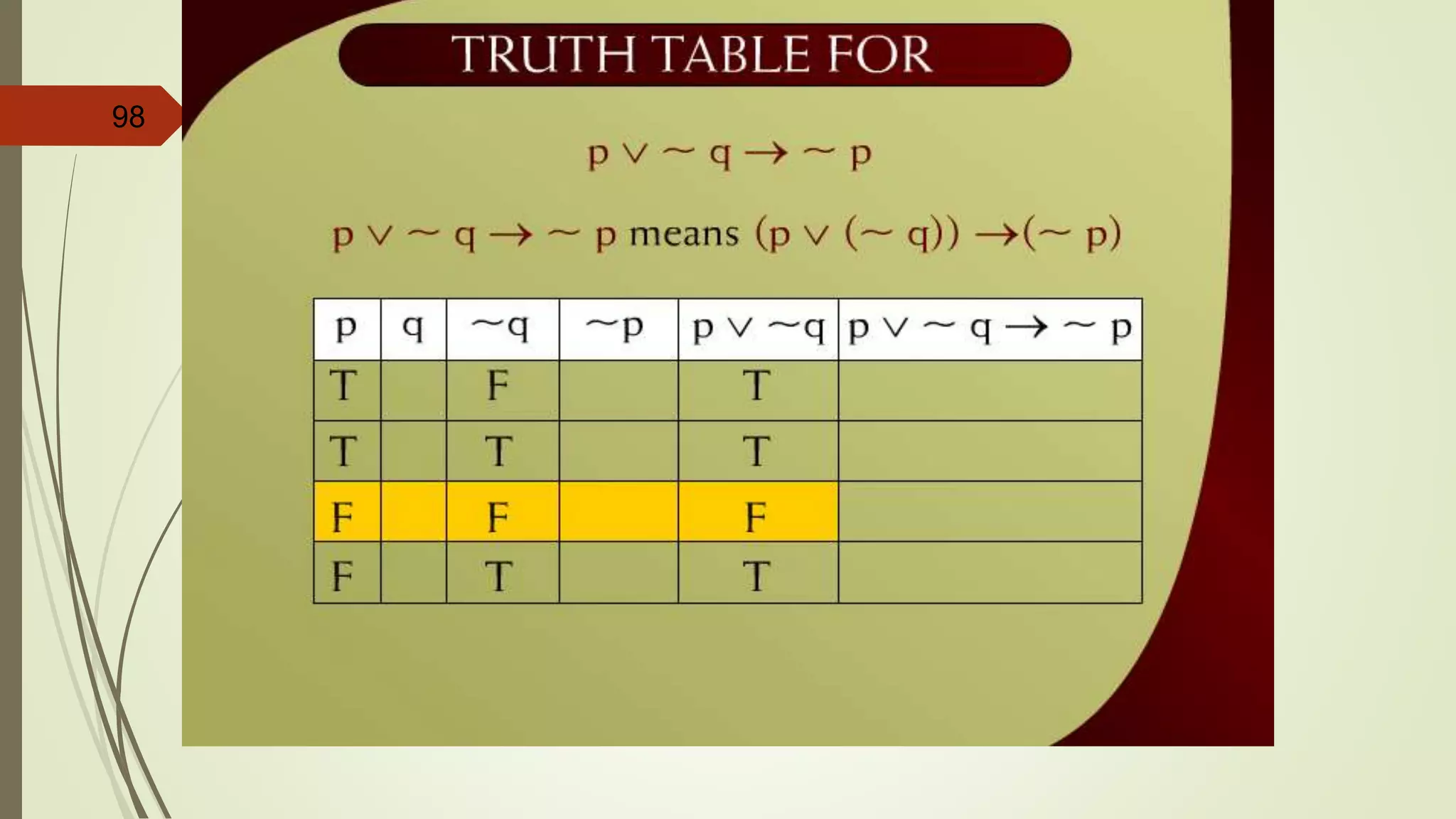
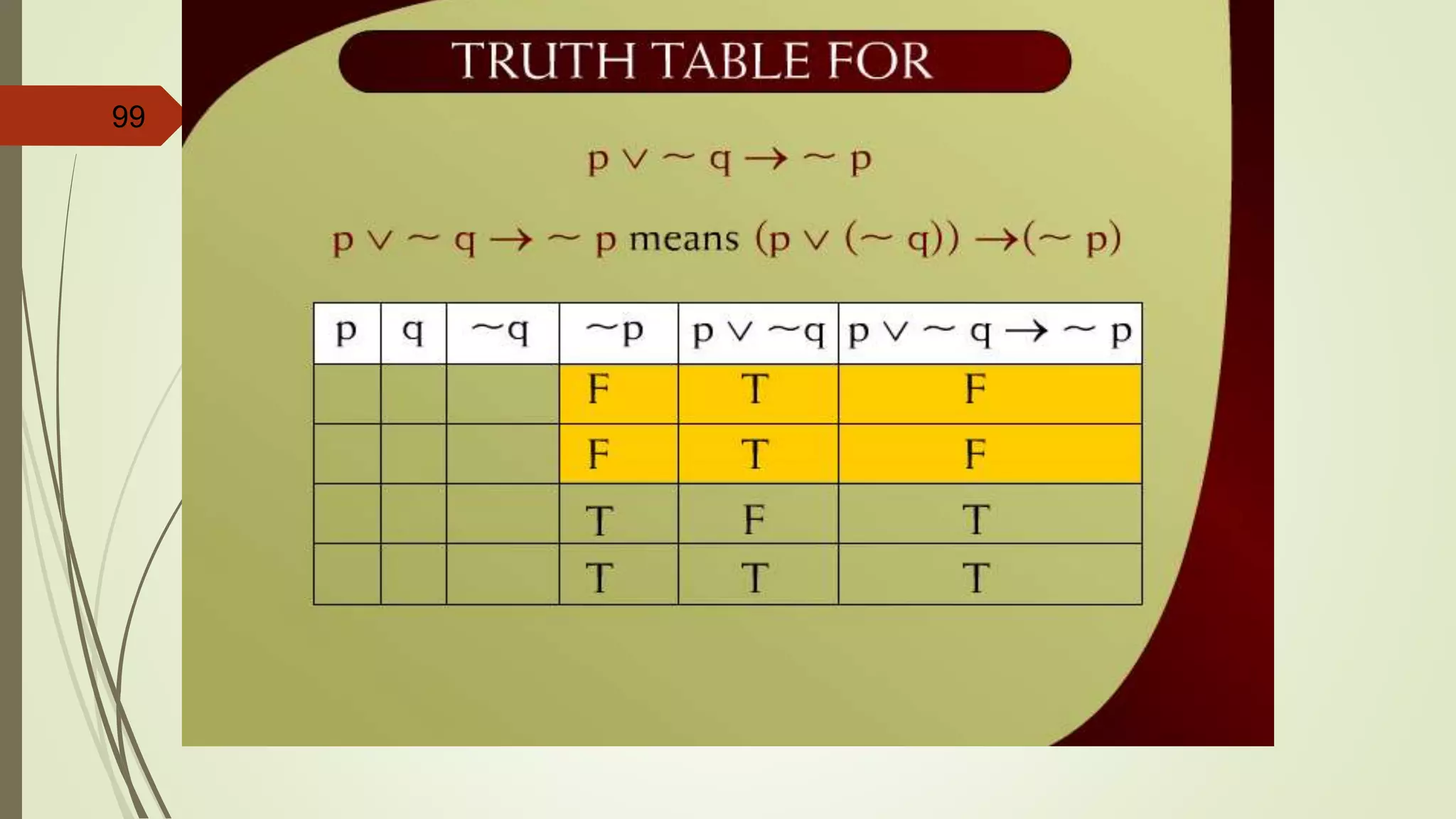
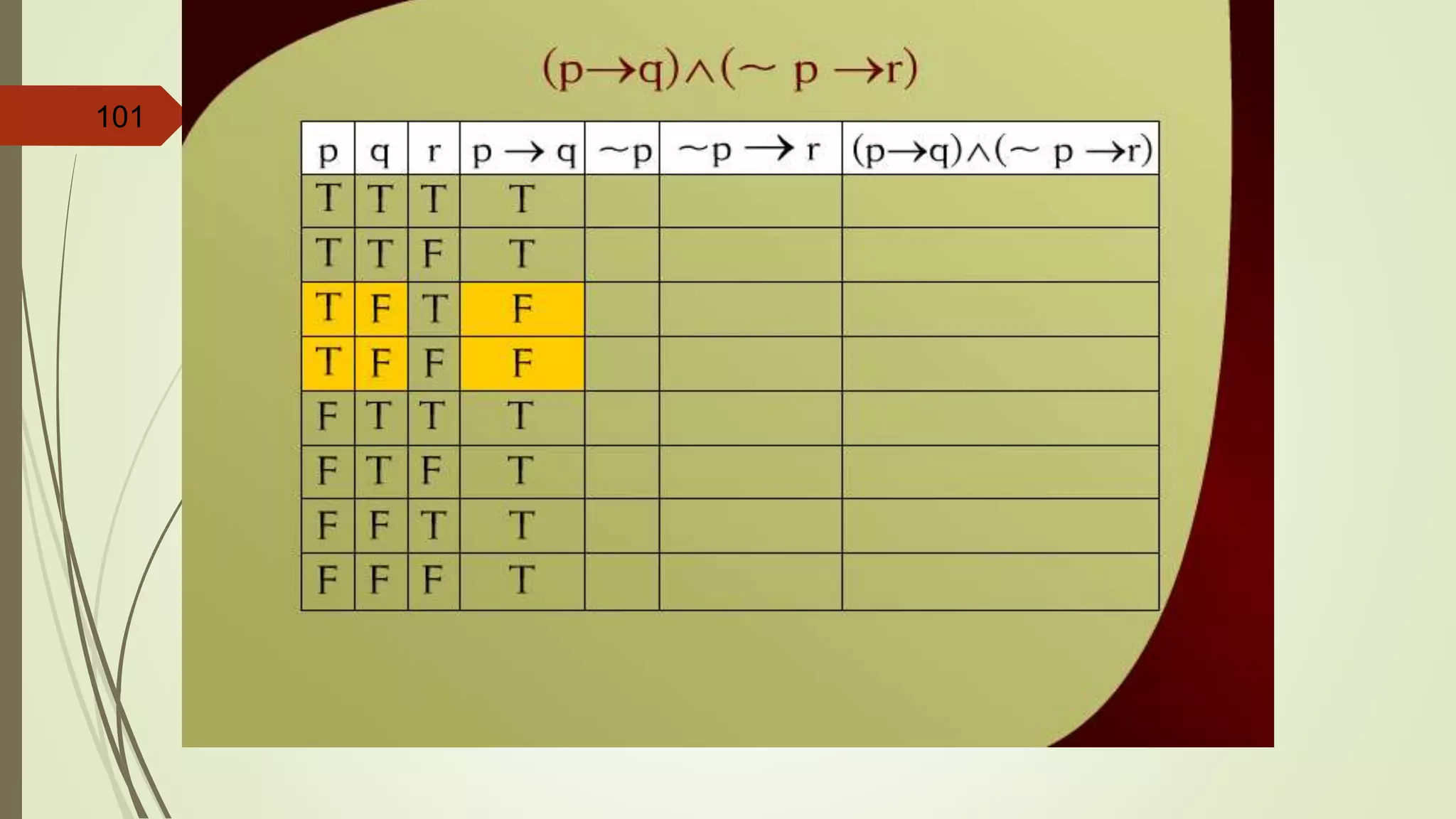
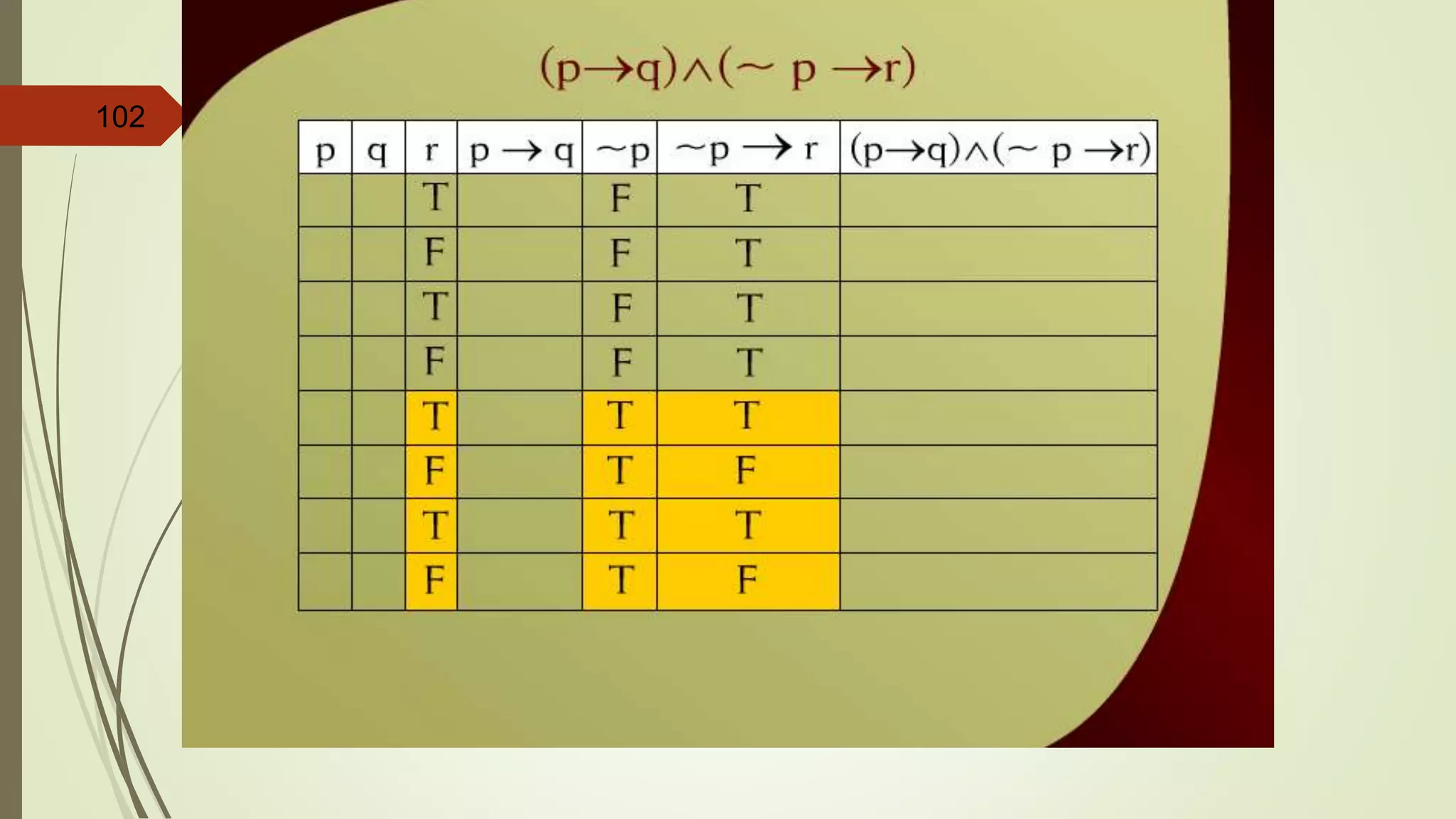
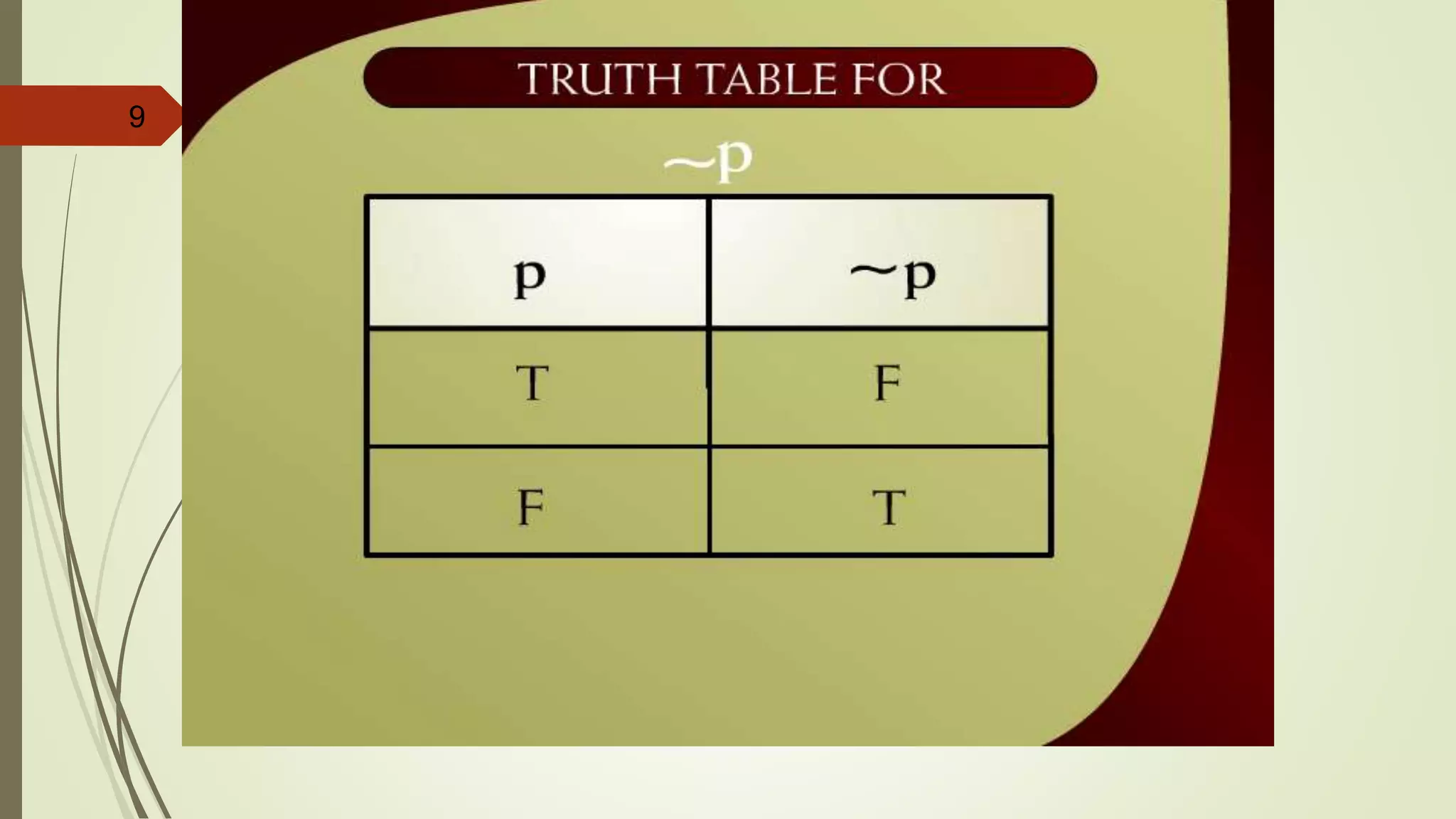
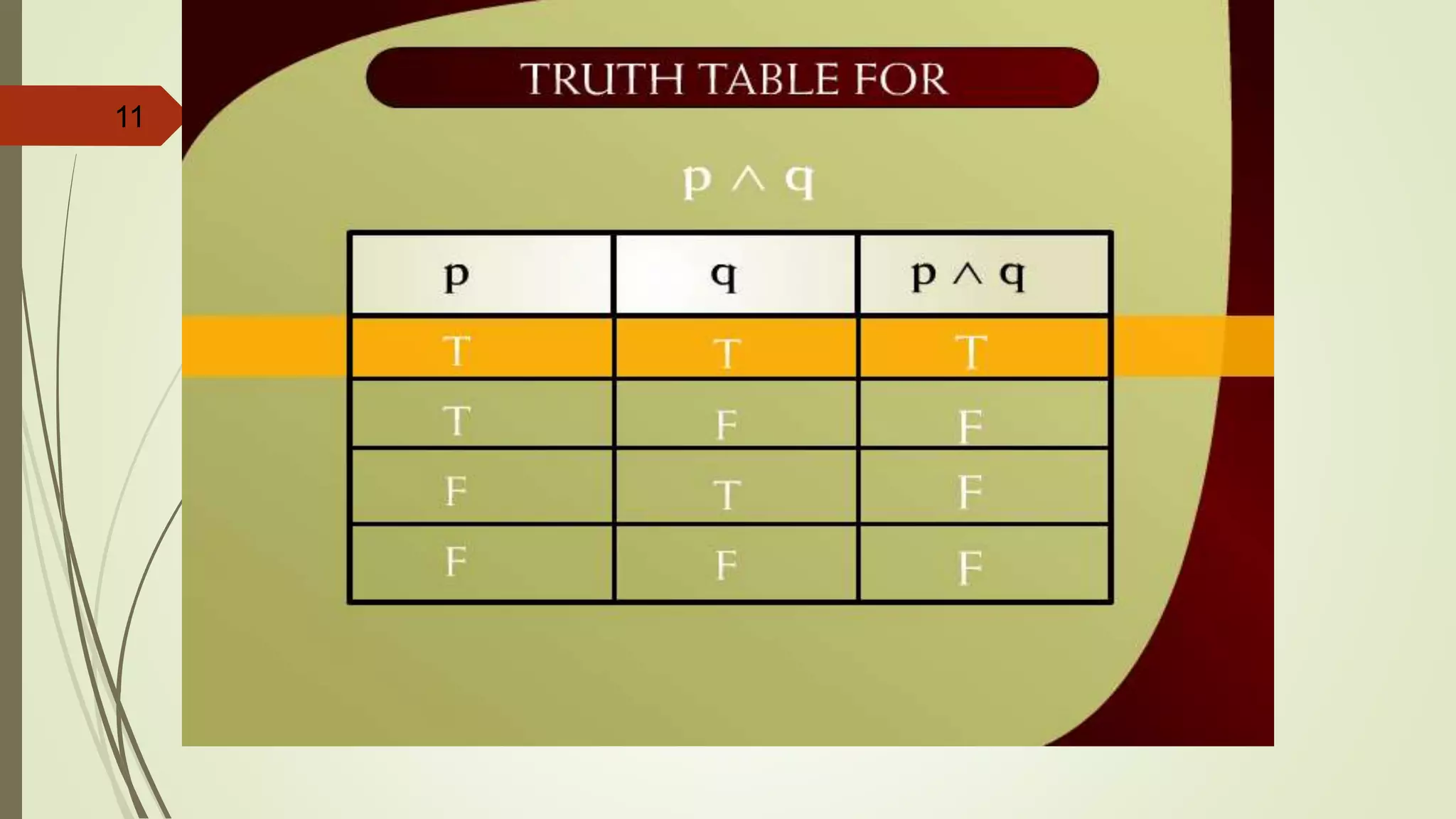
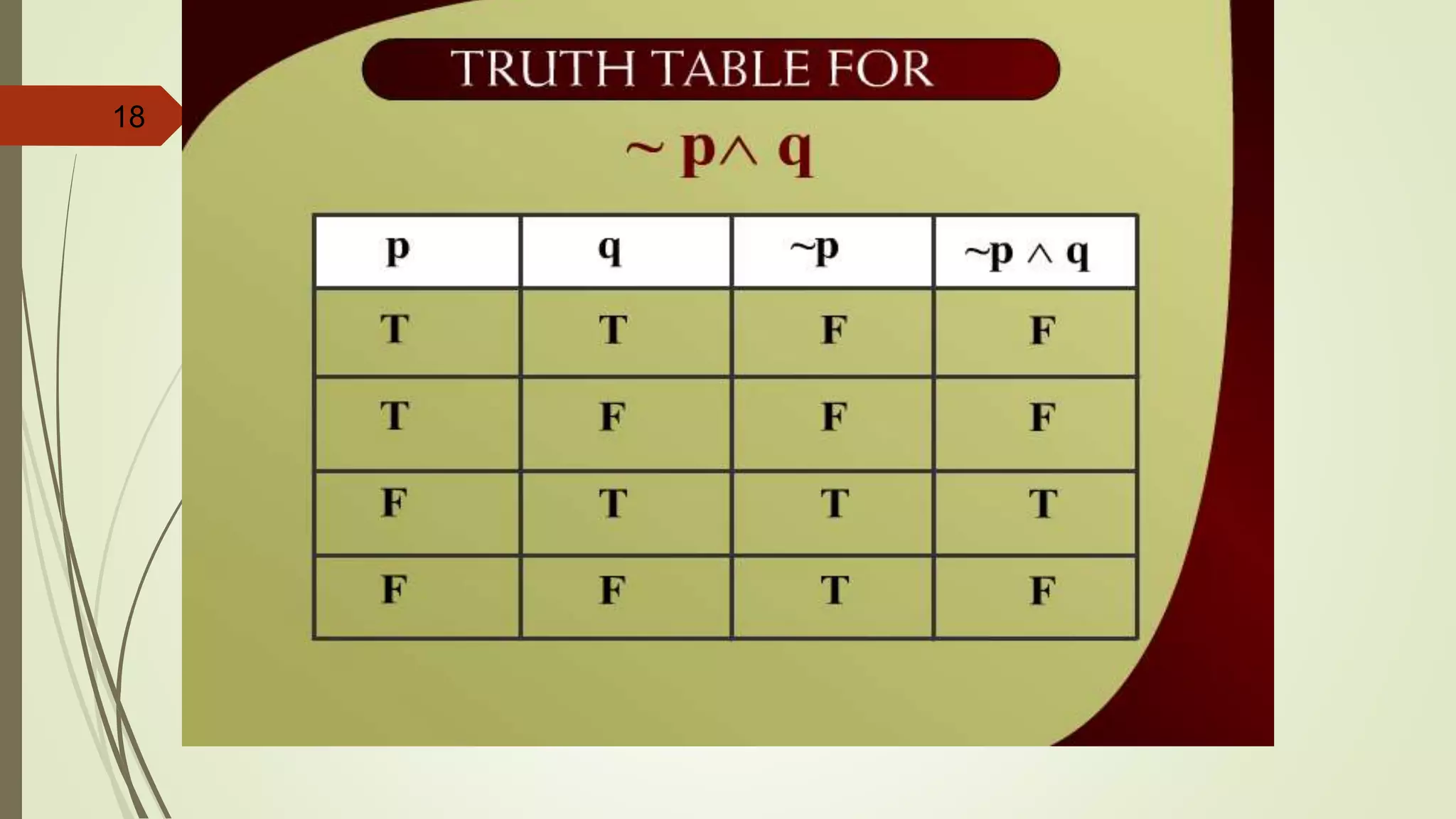
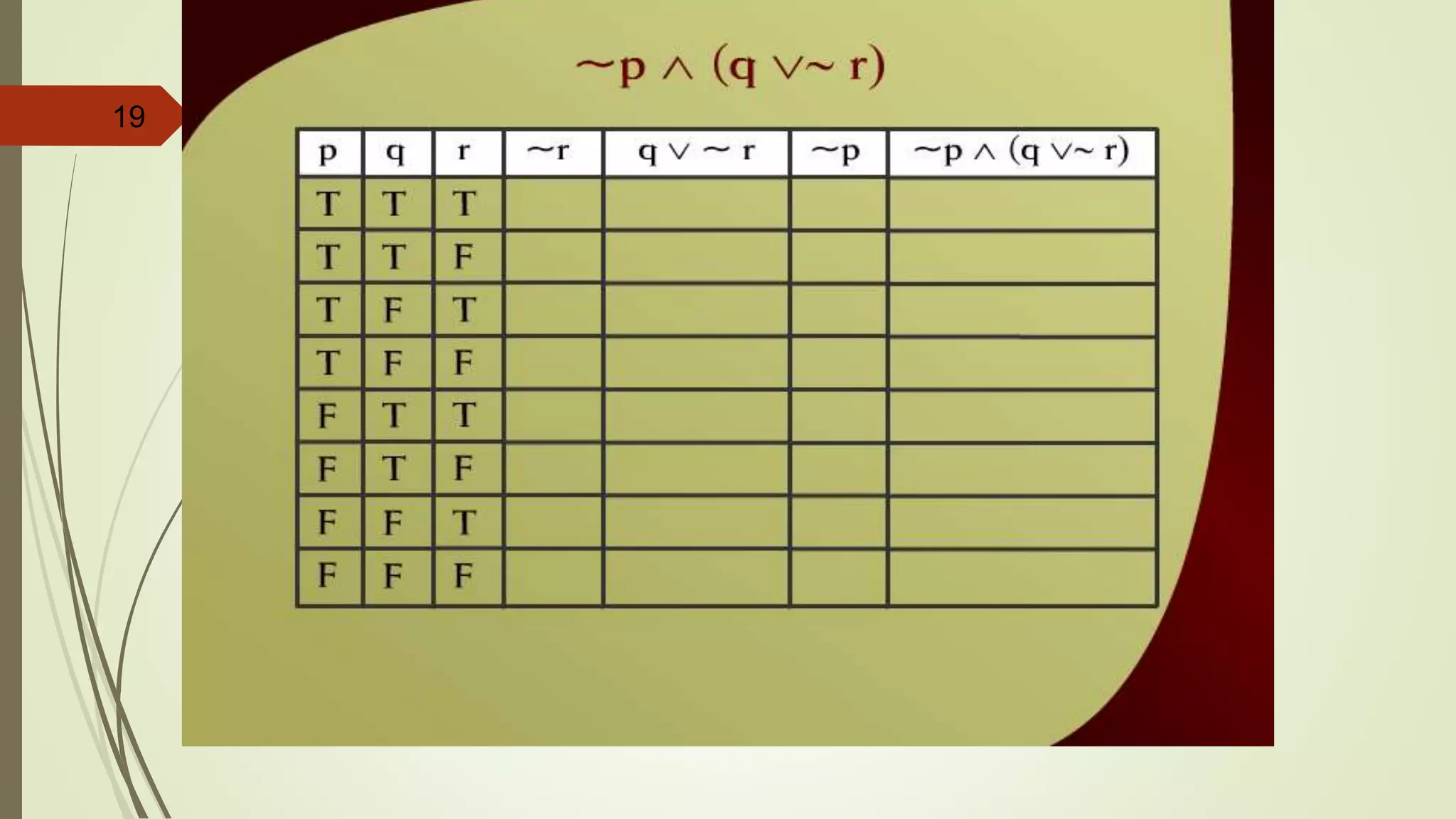
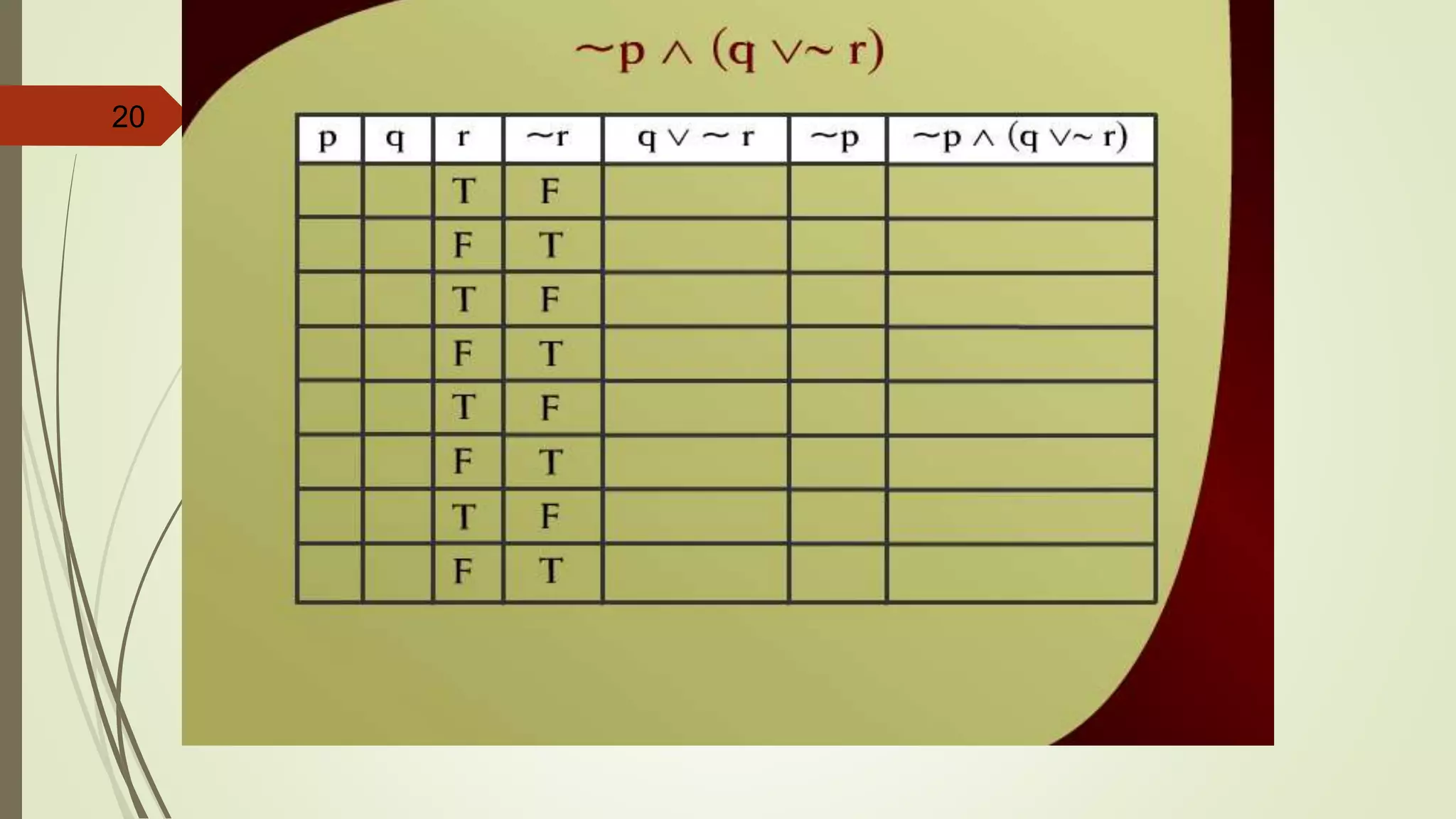
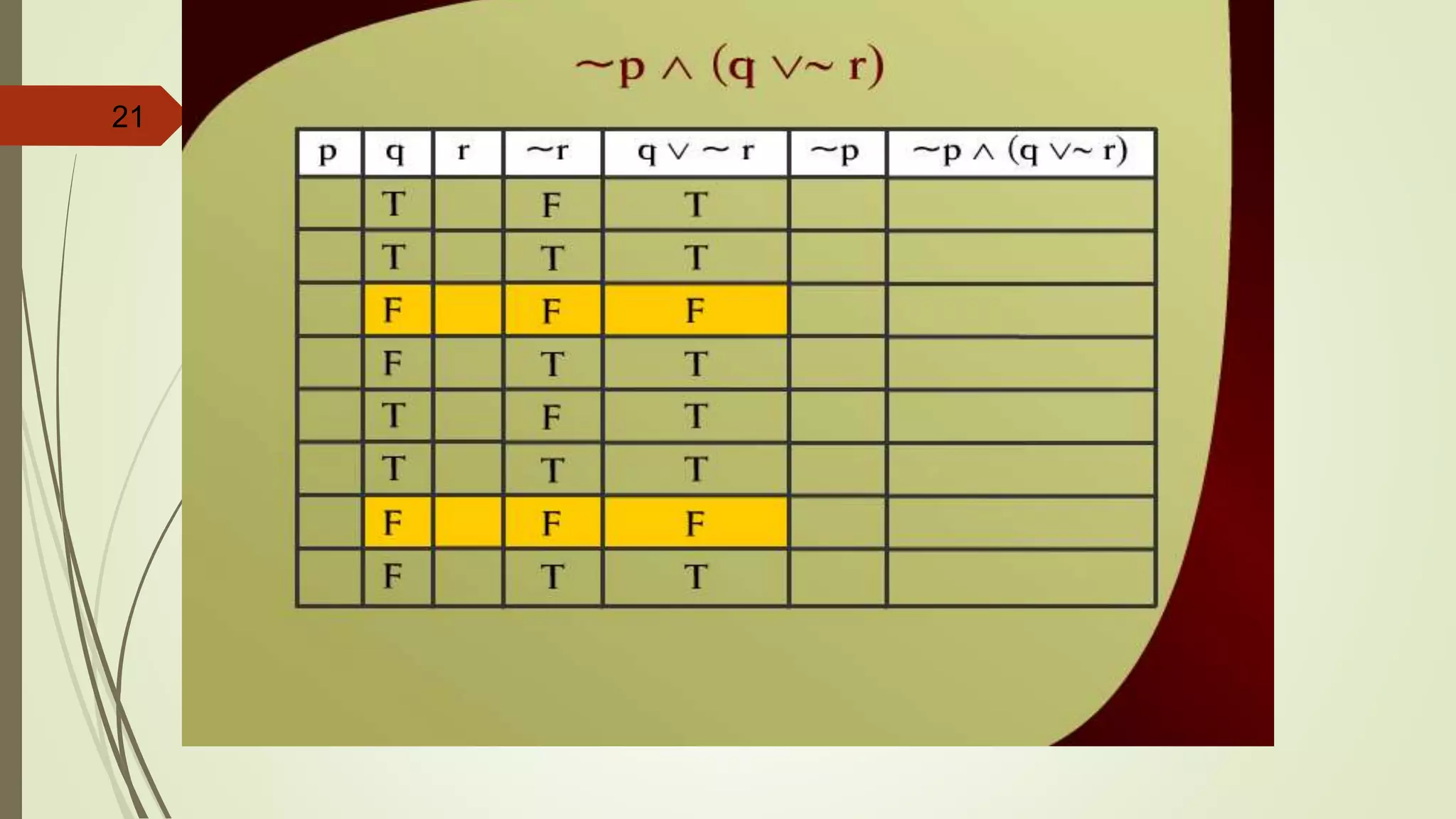
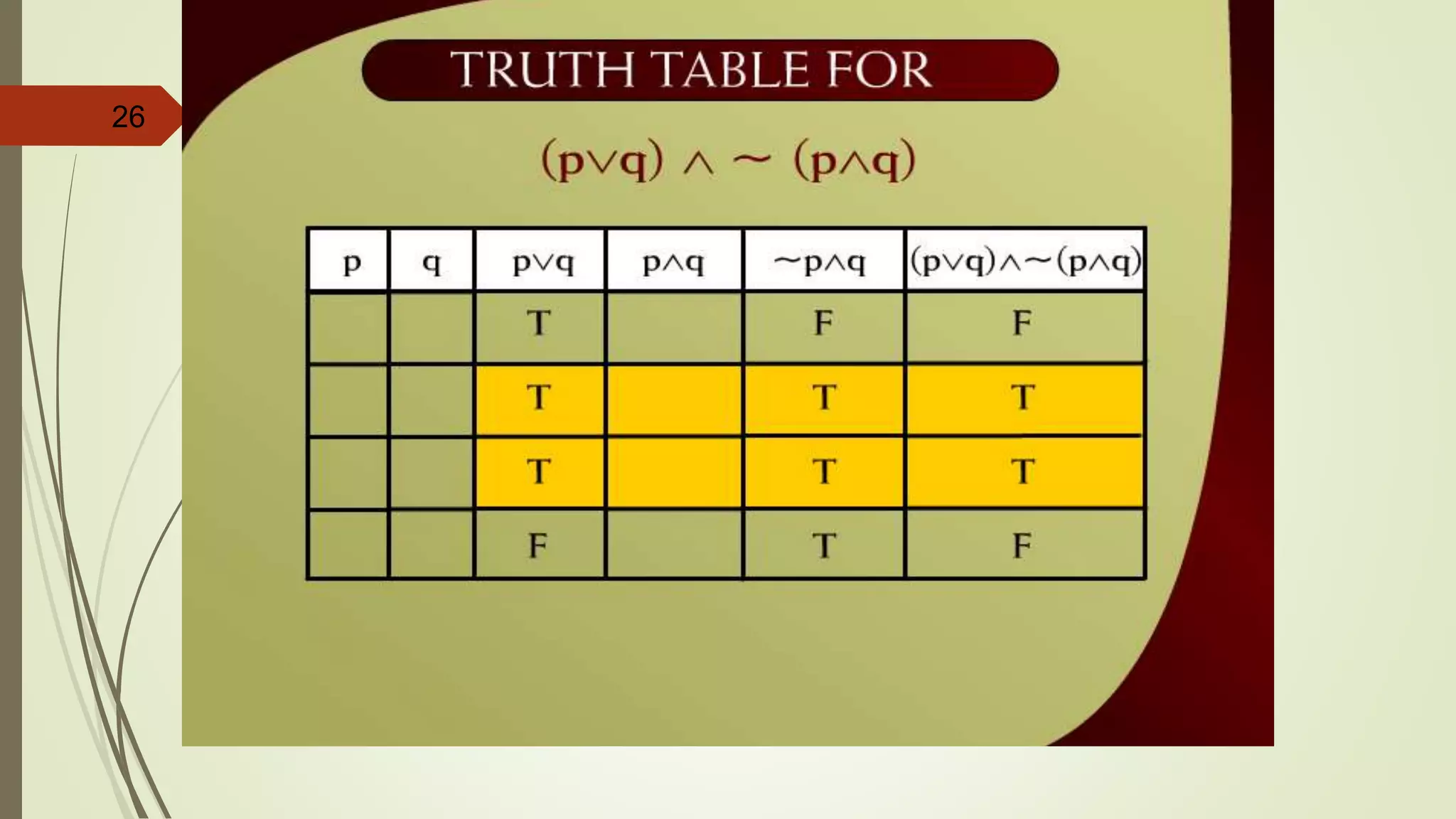
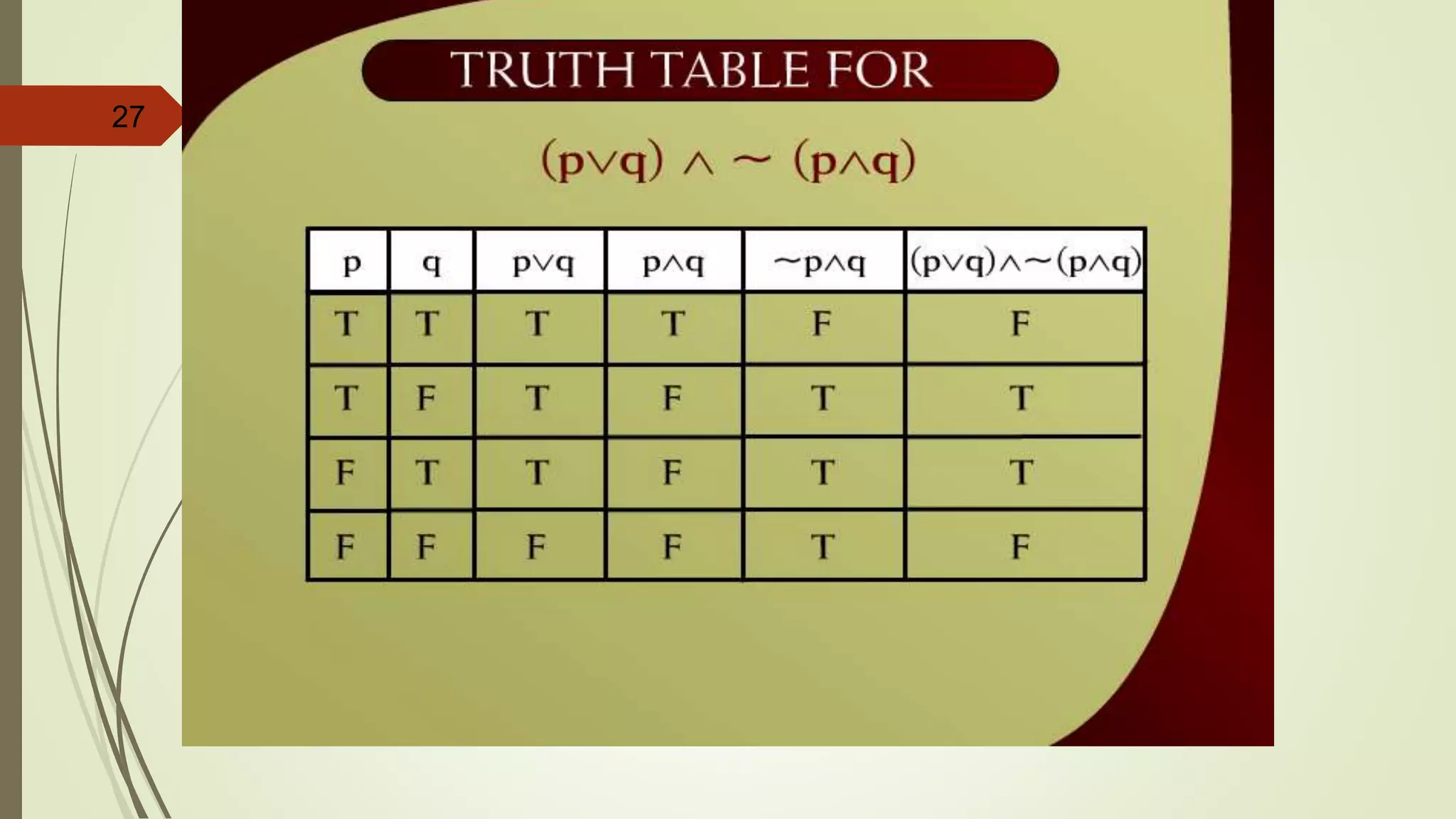
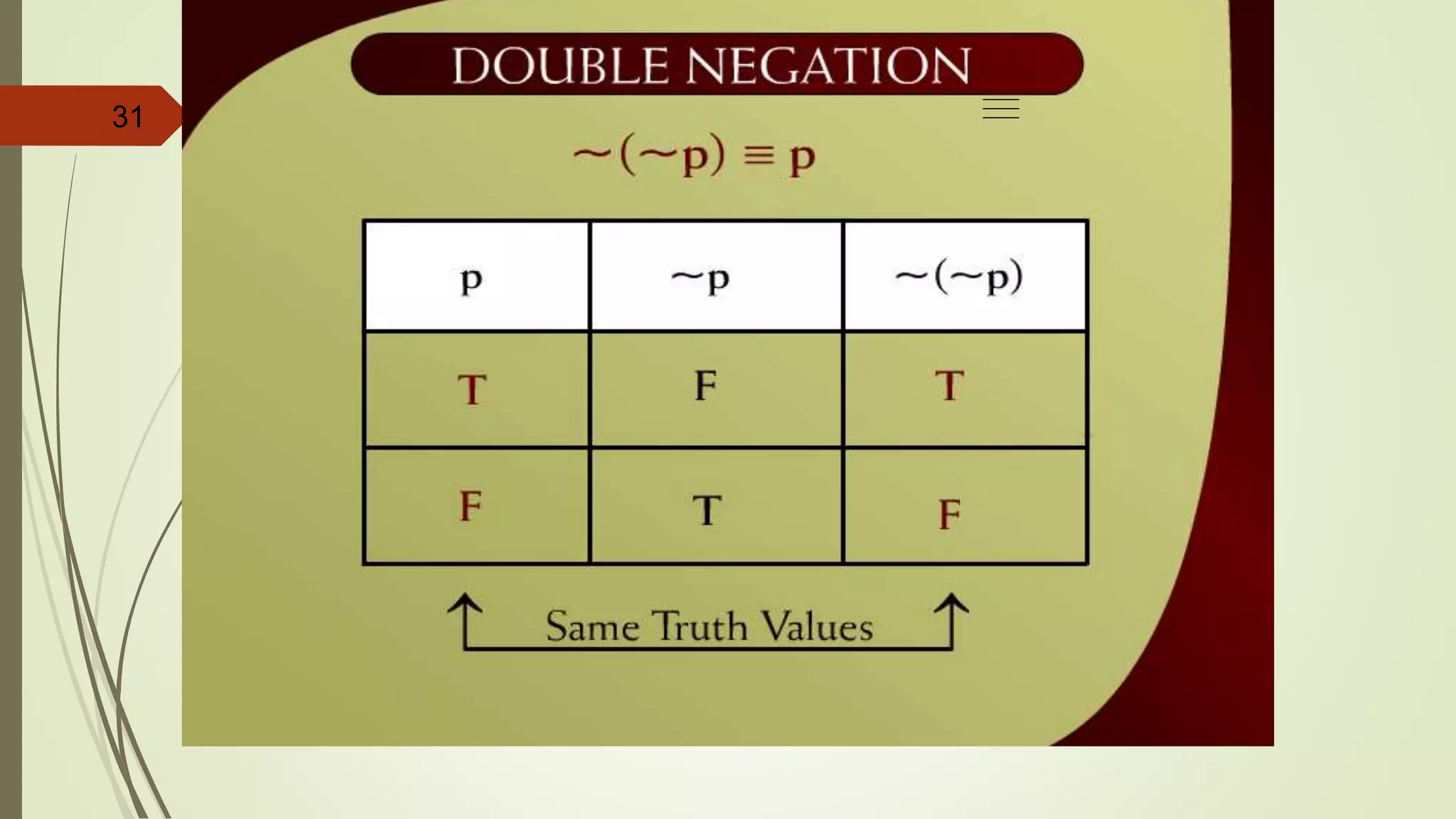
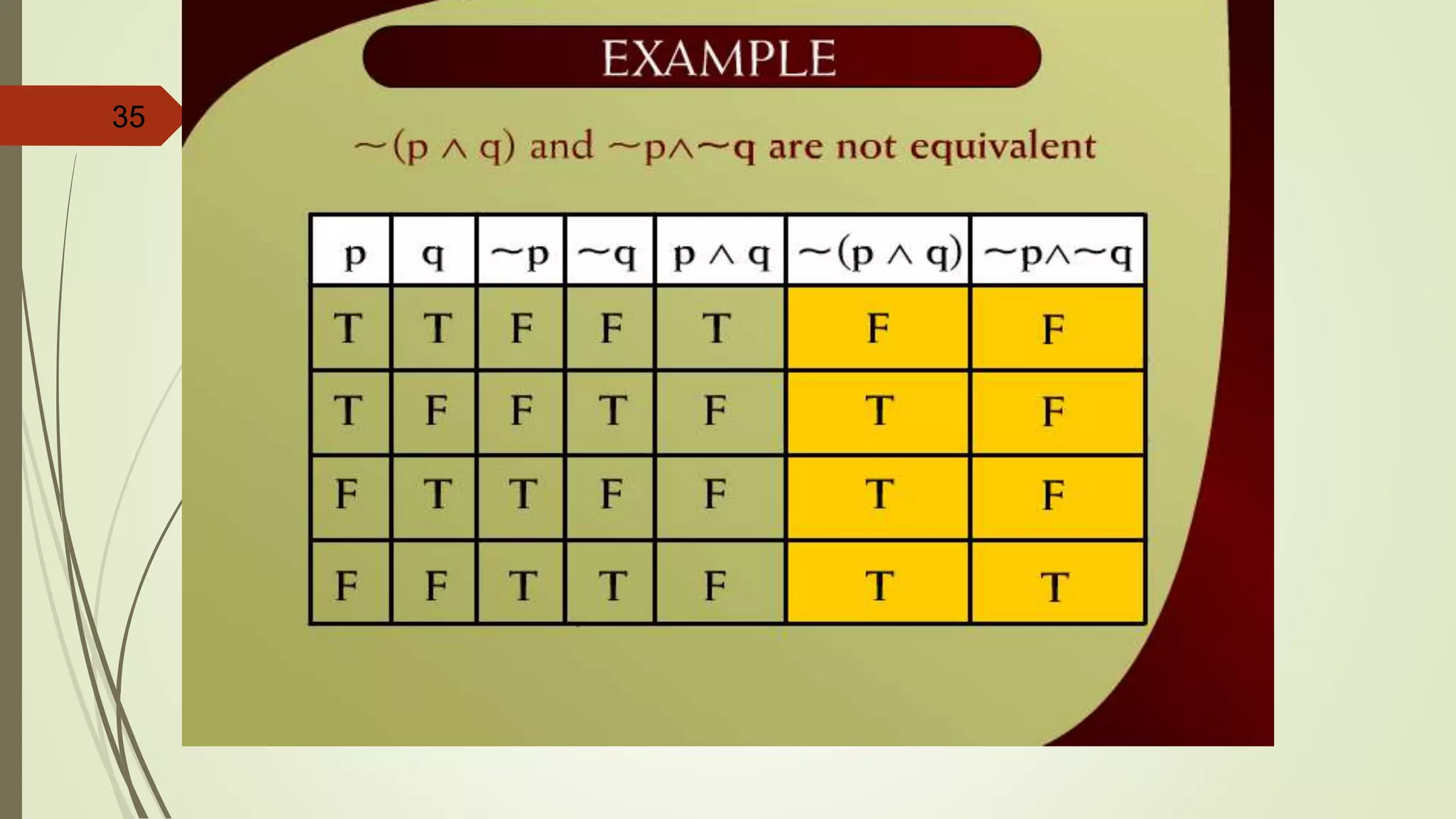
This document appears to be lecture notes on discrete structures and logic that includes examples of translating English statements to logical symbols, truth tables for various logical connectives and statements, the differences between conditional, biconditional, inverse, and contrapositive statements, and applying logical laws and properties. It discusses topics like negation, conjunction, disjunction, exclusive or, logical equivalence, De Morgan's laws, tautologies, contradictions, and simplifying logical statements.

1. Discrete Structures
Engr. Tooba Khan
Department of Computer Engineering
Lecture 01 (Cont’d.)
1

2. 2 Examples – 14b

3. 3
Translating from English to
Symbols – 15

4. 4
Translating from English to
Symbols – 16a

5. 5
Translating from English to
Symbols – 16

6. 6
Translating from English to
Symbols – 17a

7. 7
Translating from English to
Symbols – 17b

8. 8
Negation – 19

9. 9
Truth Table for ~p – 20

10. 10
Conjunction – 21

11. 11
Truth Table for p ^ q – 22

12. 12 Disjunction – 23

13. 13
Truth Table for p q – 15

14. 14
Truth Table

15. 15 Truth Table for ~p^q - 2

16. 16 Truth Table for ~p^q – 2a

17. 17
Truth Table for ~p^q – 2b

18. 18 Truth Table for ~p^q – 2c

19. 19 ~p ^ (q v~ r) – (2 - 3a)

20. 20 ~p ^ (q v~ r) – 2 - 3b

21. 21 ~p ^ (q v~ r) – 2 - 3c

22. 22 ~p ^ (q v~ r) – 2 - 3d

23. 23 Truth Table for ~p (p v~ q) – 2 - 3e
v

24. 24 Truth Table for (pvq) ^~ (p^q) – 2 - 4a

25. 25
Truth Table for (pvq) ^~ (p^q) – 2 -
4c

26. 26
Truth Table for (pvq) ^~ (p^q) – 2 -
4e
v
v

27. 27
Truth Table for (pvq) ^~ (p^q) – 2 -
4f

28. 28 Exclusive OR – 2 - 5

29. 29 Symbols for Exclusive OR – 2 - 5a

30. 30 Logical Equivalence – 2 - 6

31. 31 Double Negation ~(~p) ≡ p – 2 - 7

32. 32 Examples – 2 - 12

33. 33 Example – 2 - 17c

34. 34 Example – 2 - 17d

35. 35 Example – 2 - 17e

36. 36 De Morgan’s Laws – 2 - 9

37. 37 De Morgan’s Laws – 2 - 9a

38. 38 Proof – 2 - 16

39. 39 Proof – 2 - 16d

40. 40 Application – 2 - 10

41. 41 Exercise – 2 - 19

42. 42 Tautology – 2 - 21

43. 43 Example – 2 - 21a

44. 44 Contradiction – 2 - 22

45. 45 Example – 2 - 22a

46. ( p  q )  (~ p  ( p  ~q ))
Tautology or not

47. (p  ~q) (~pq)
Contradiction or not

48. 48 Exercise – 2 - 23

49. 49 Exercise – 2 - 24

50. 50 Laws of Logic – 2 - 25

51. 51 Laws of Logic – 2 - 25a

52. 52 Laws of Logic – 2 - 25b

53. 53 Laws of Logic – 2 - 25c

54. 54 Laws of Logic – 2 - 25d

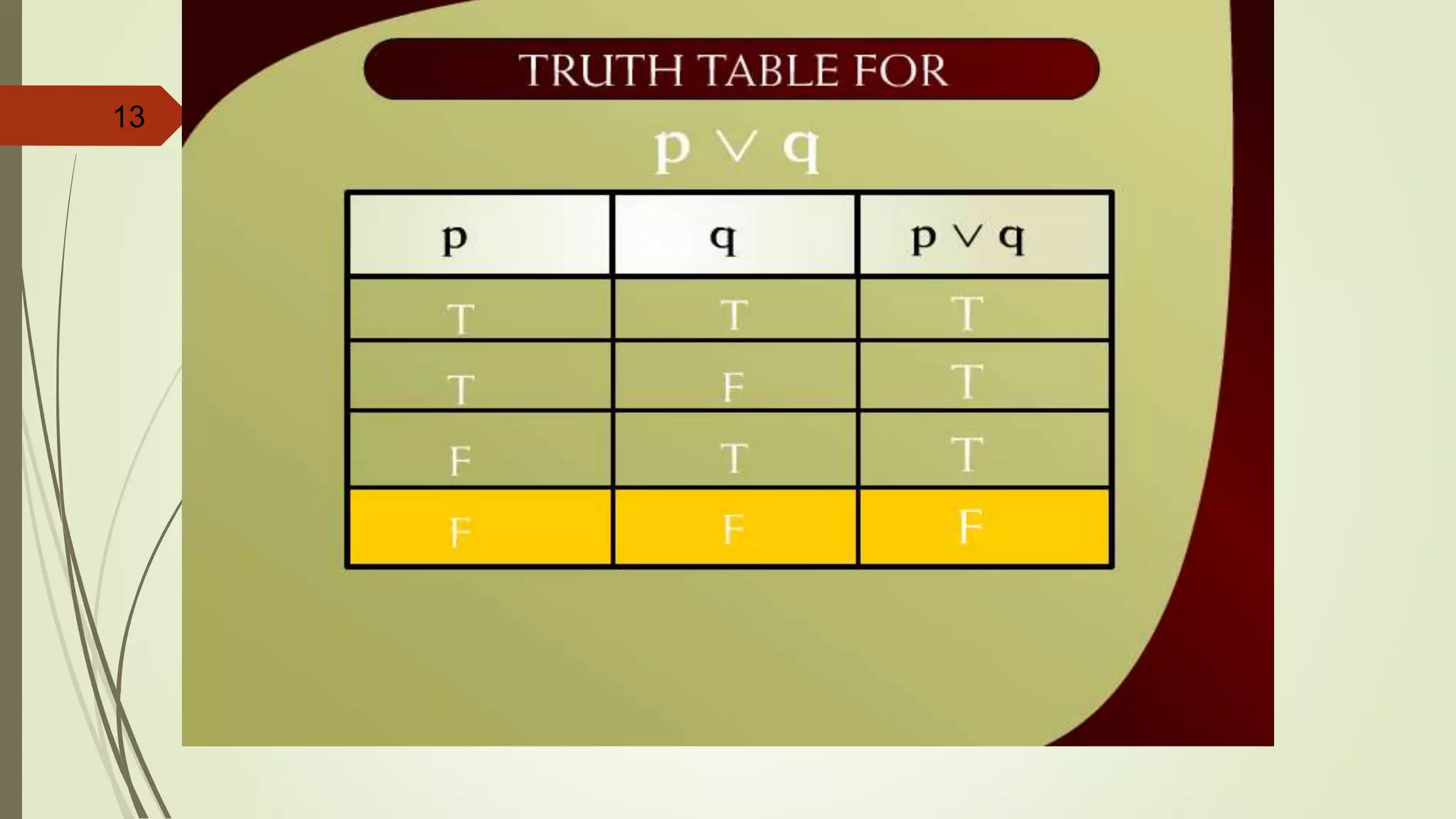
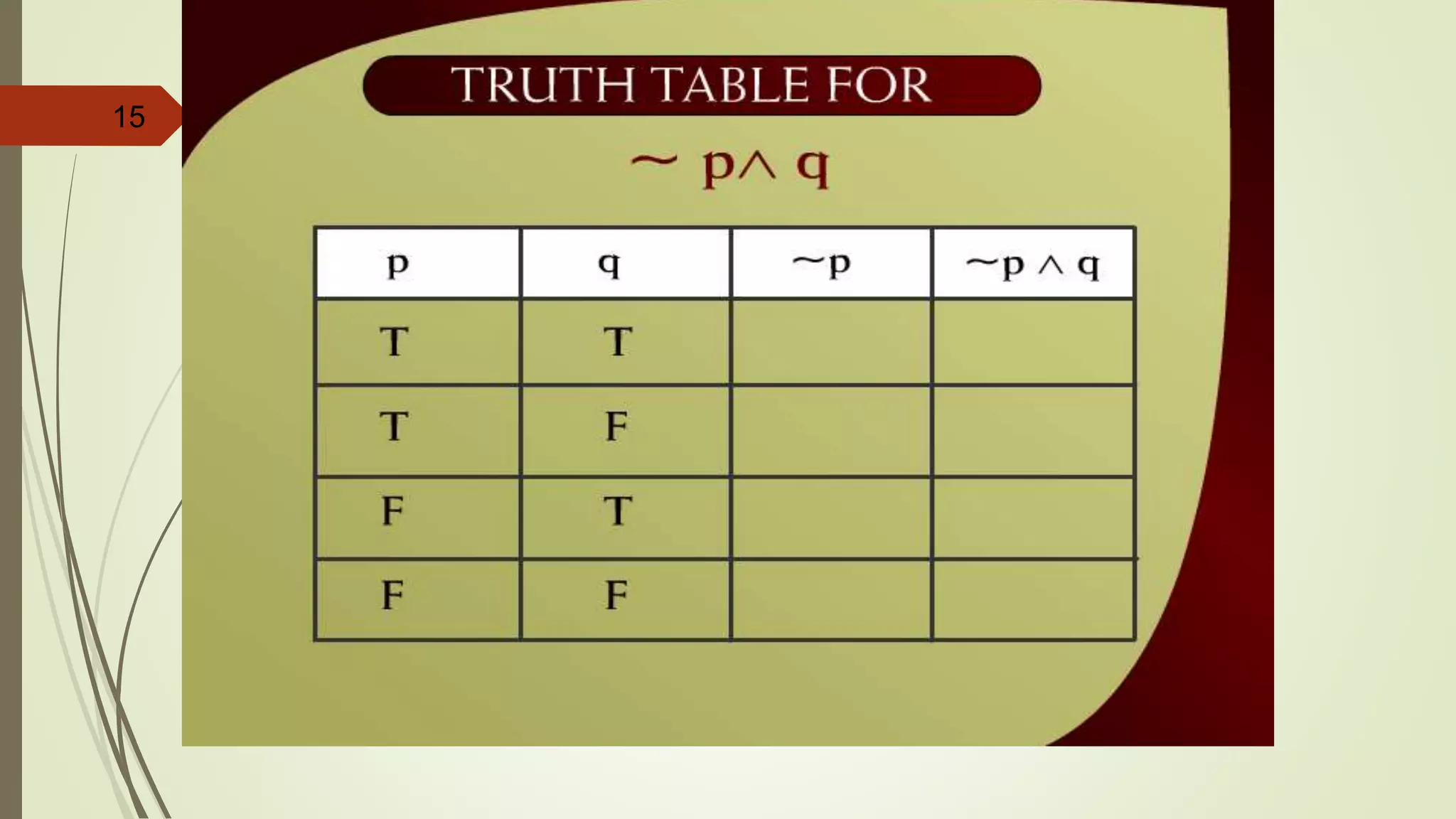
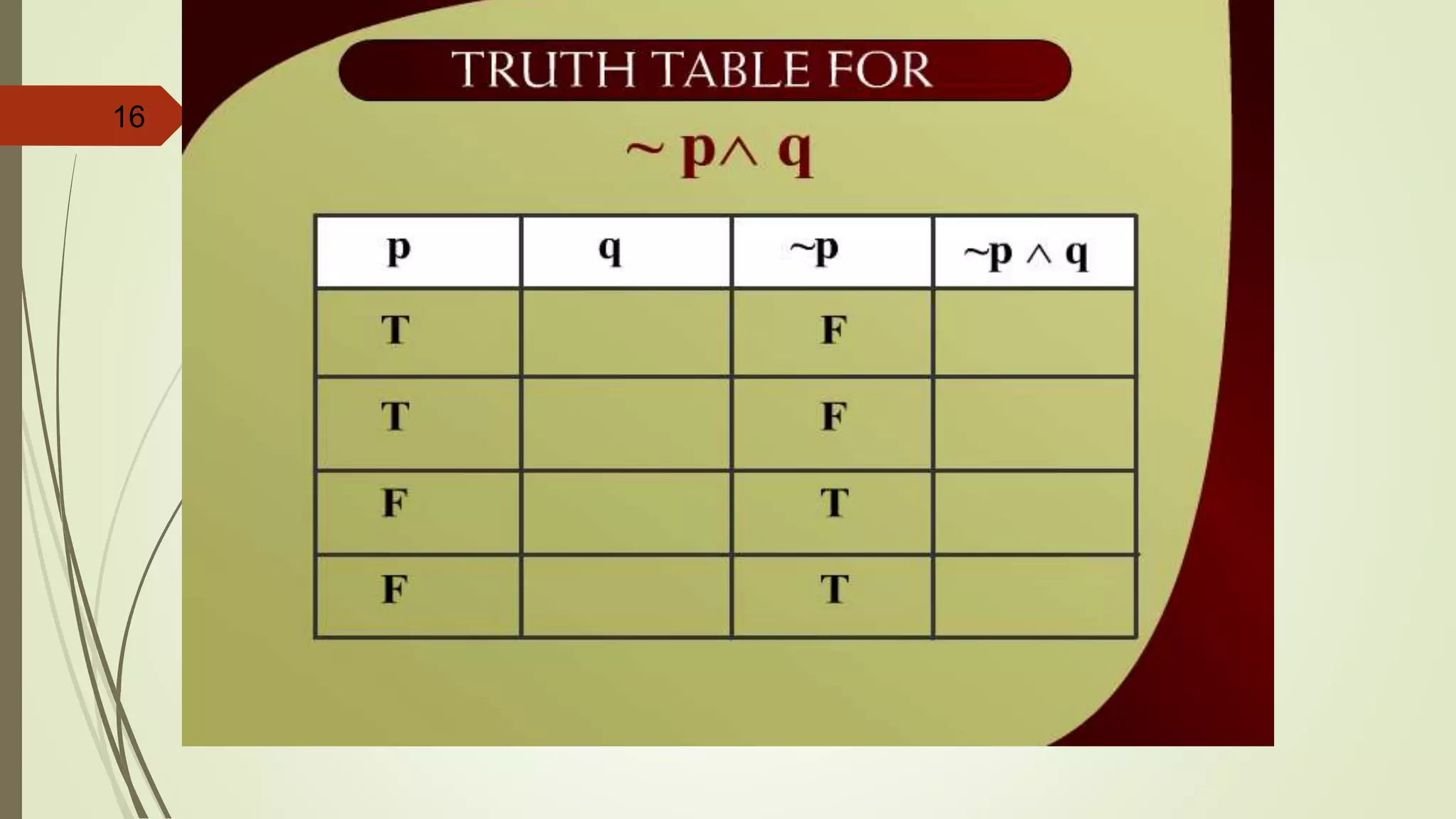
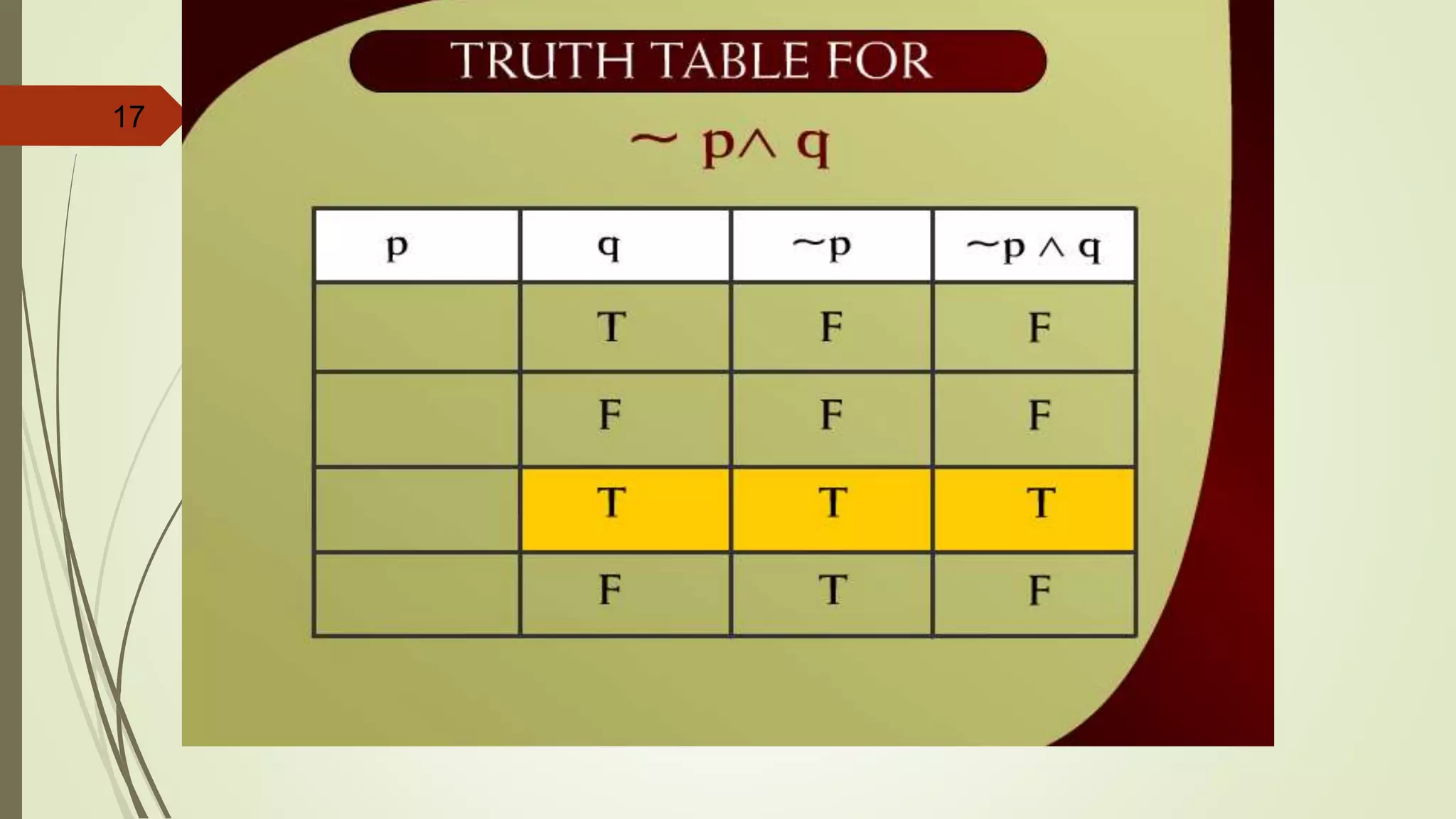
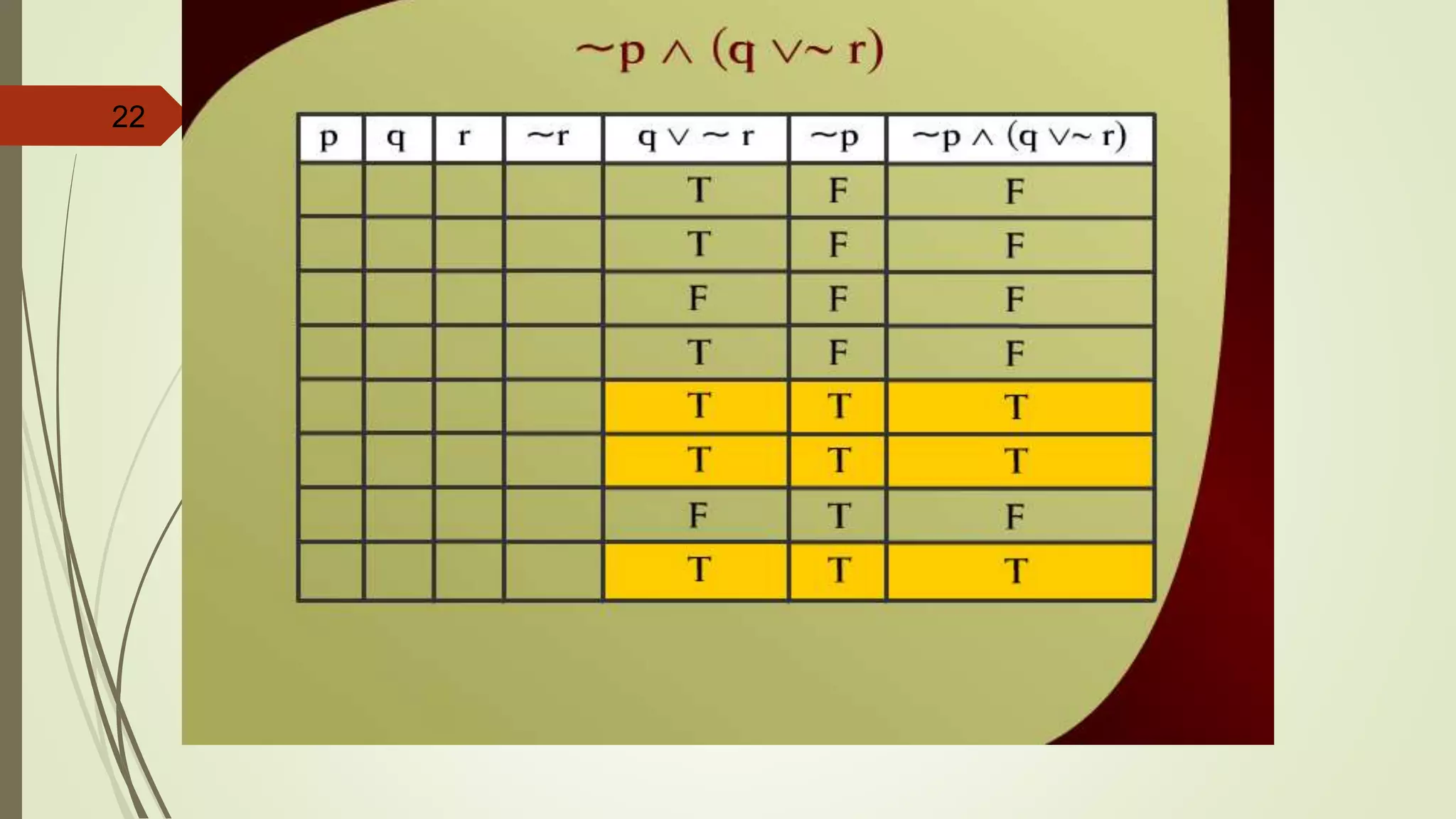
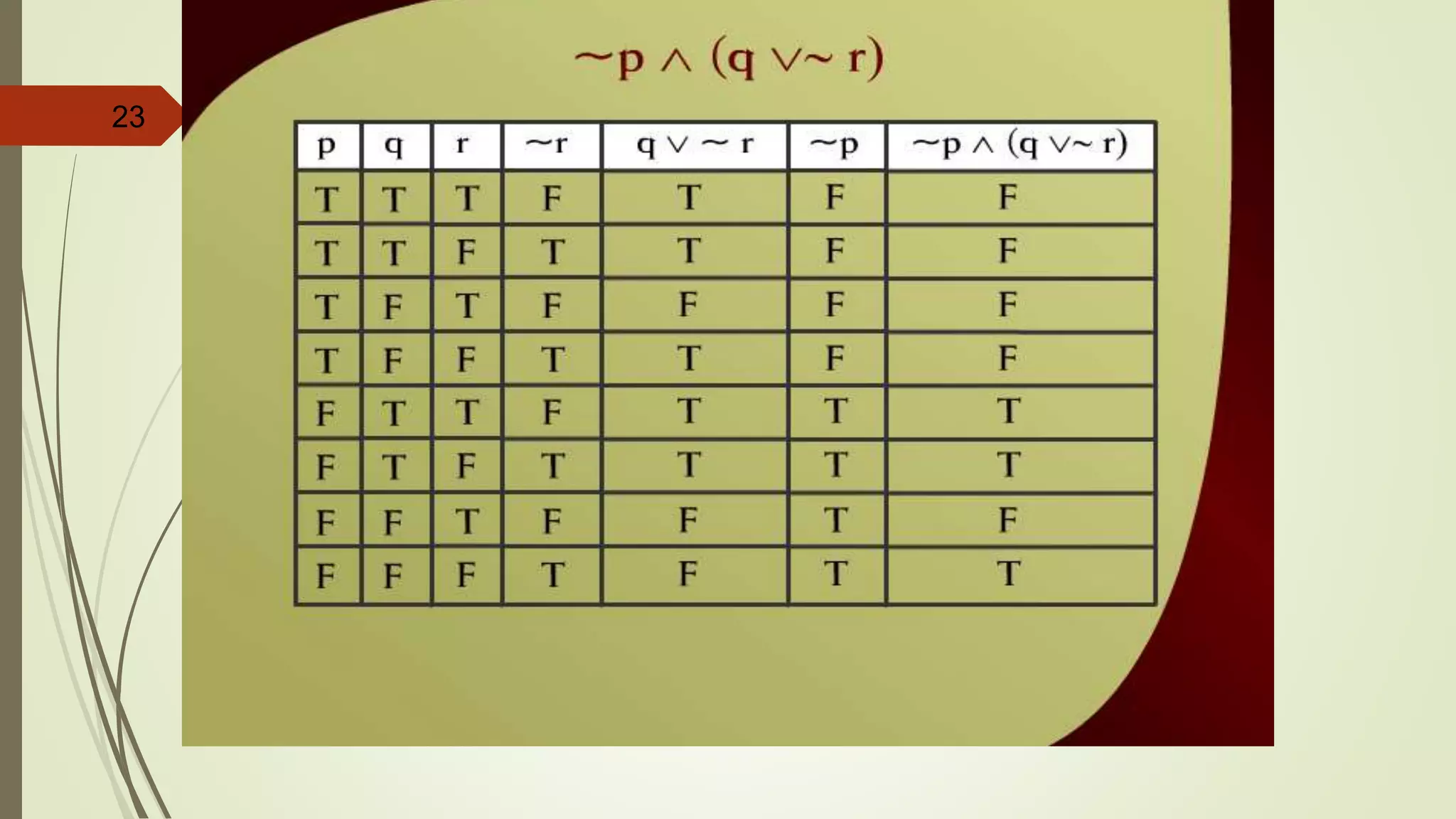
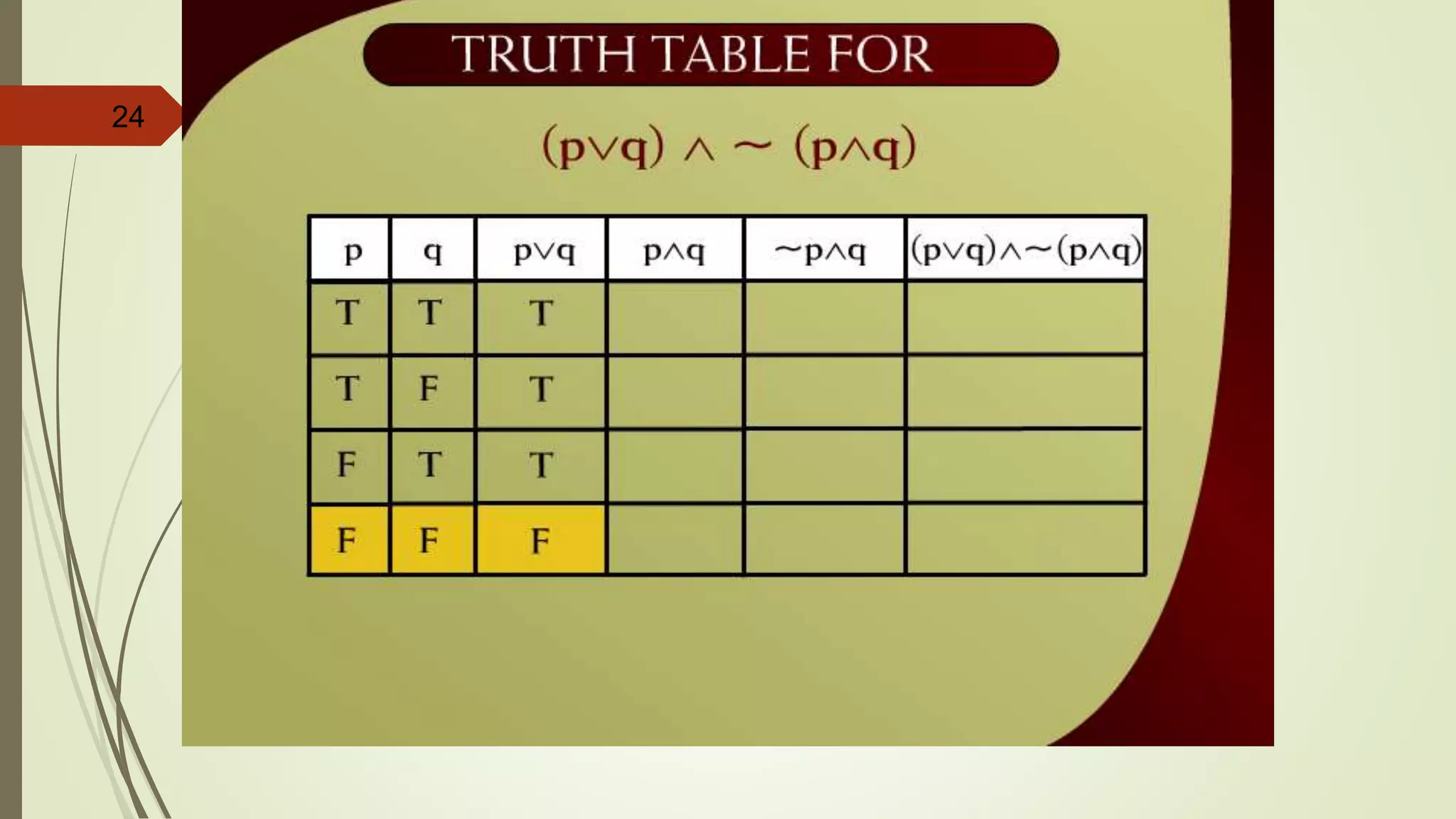
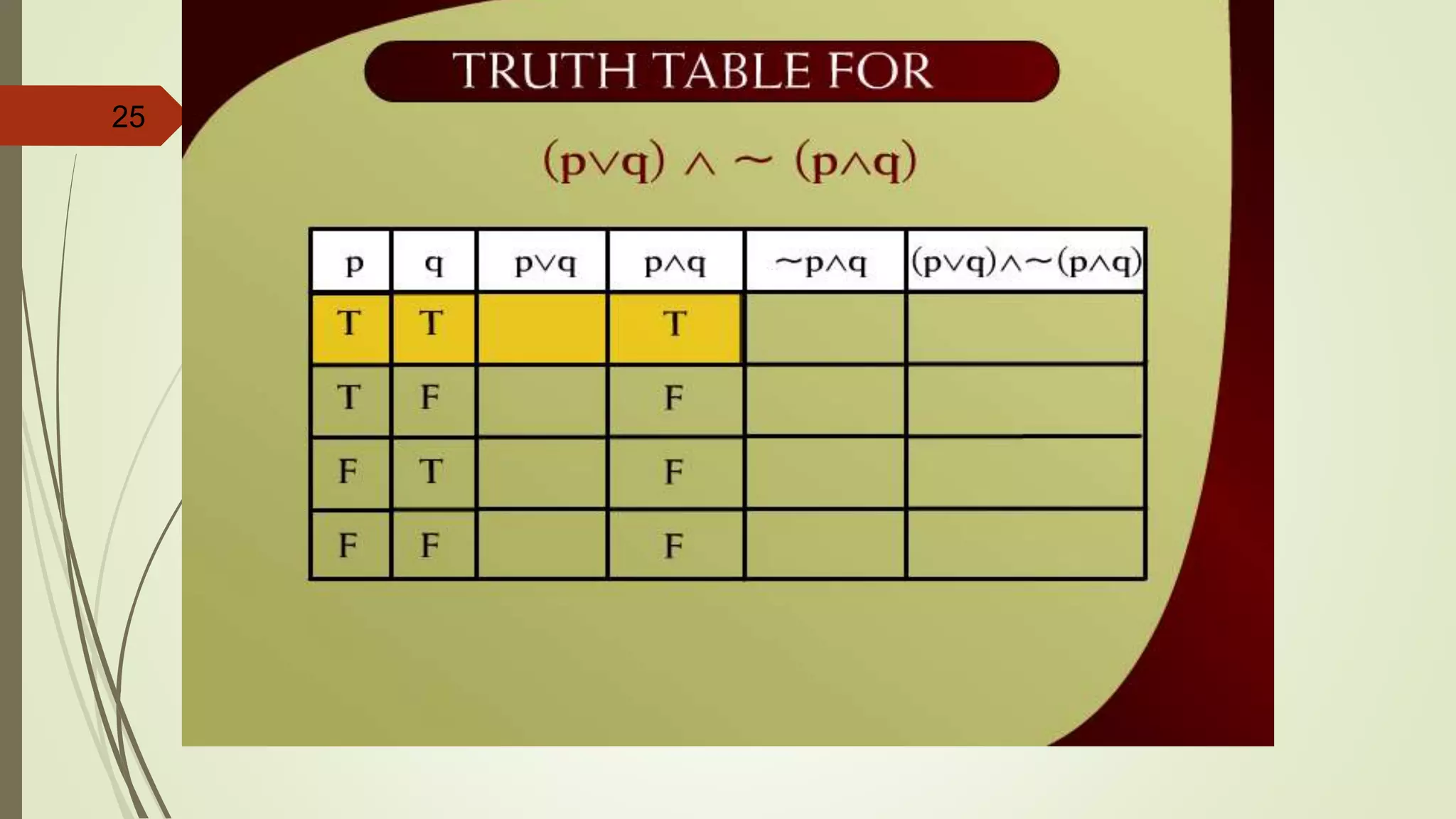
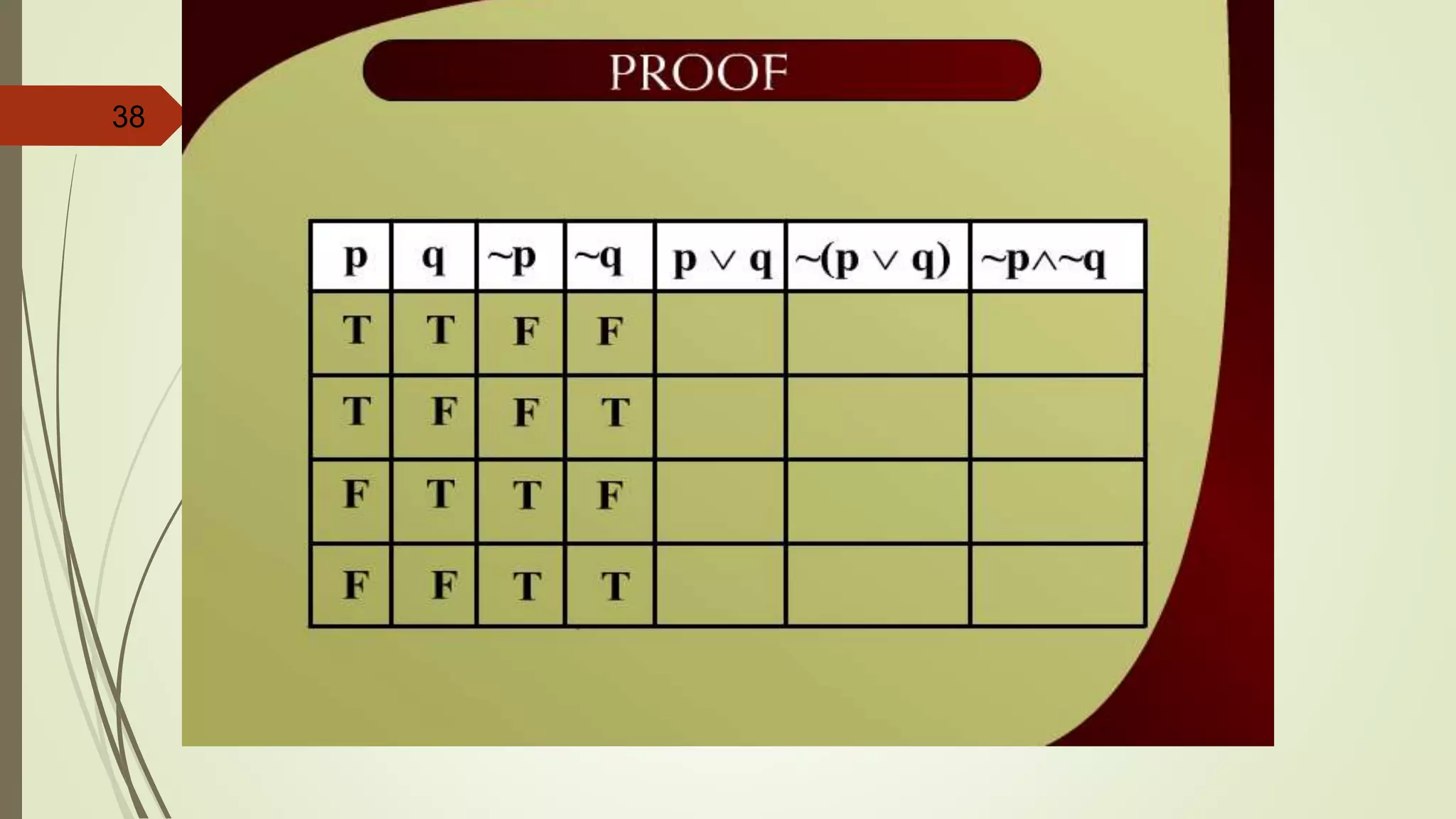
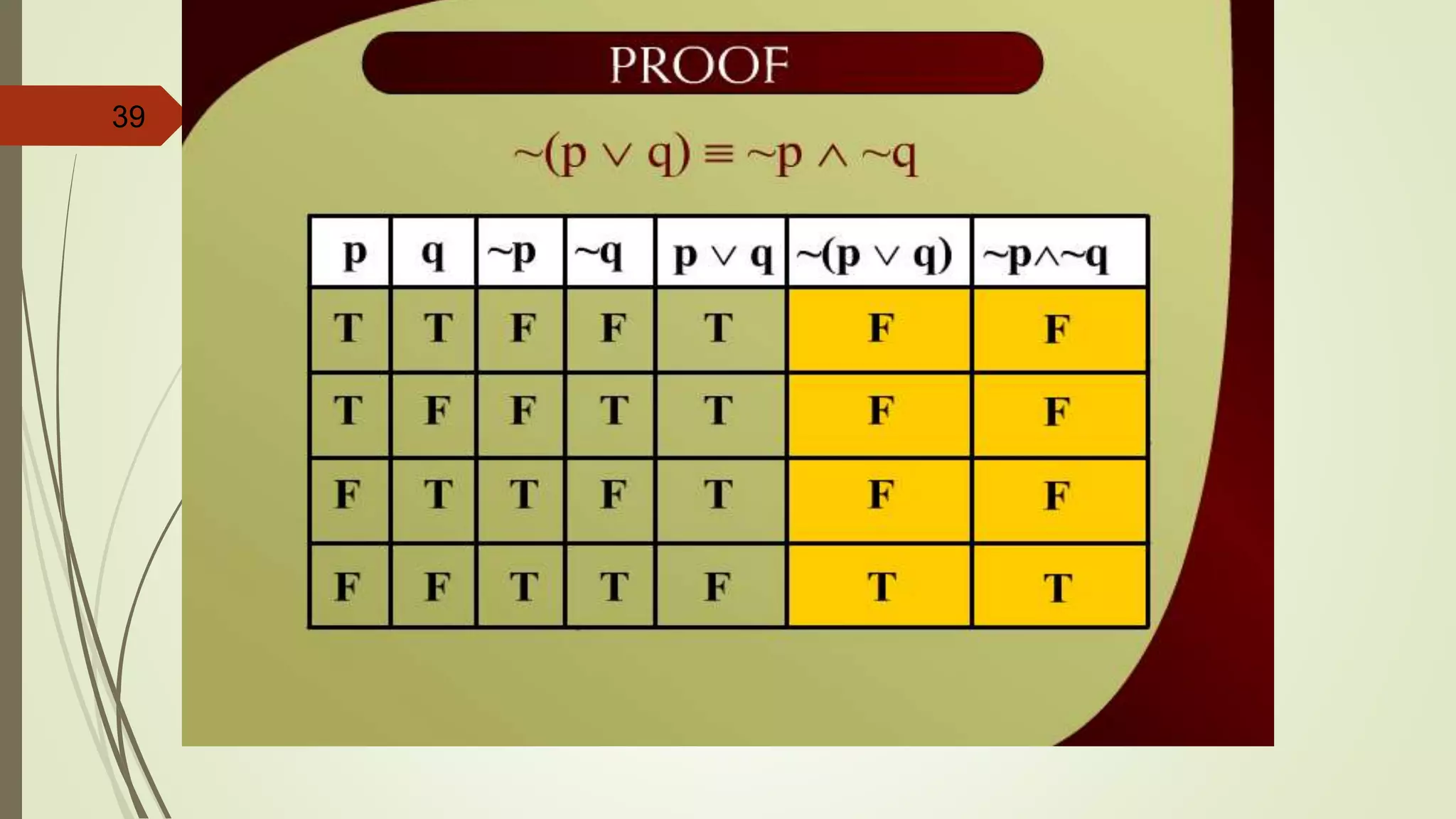
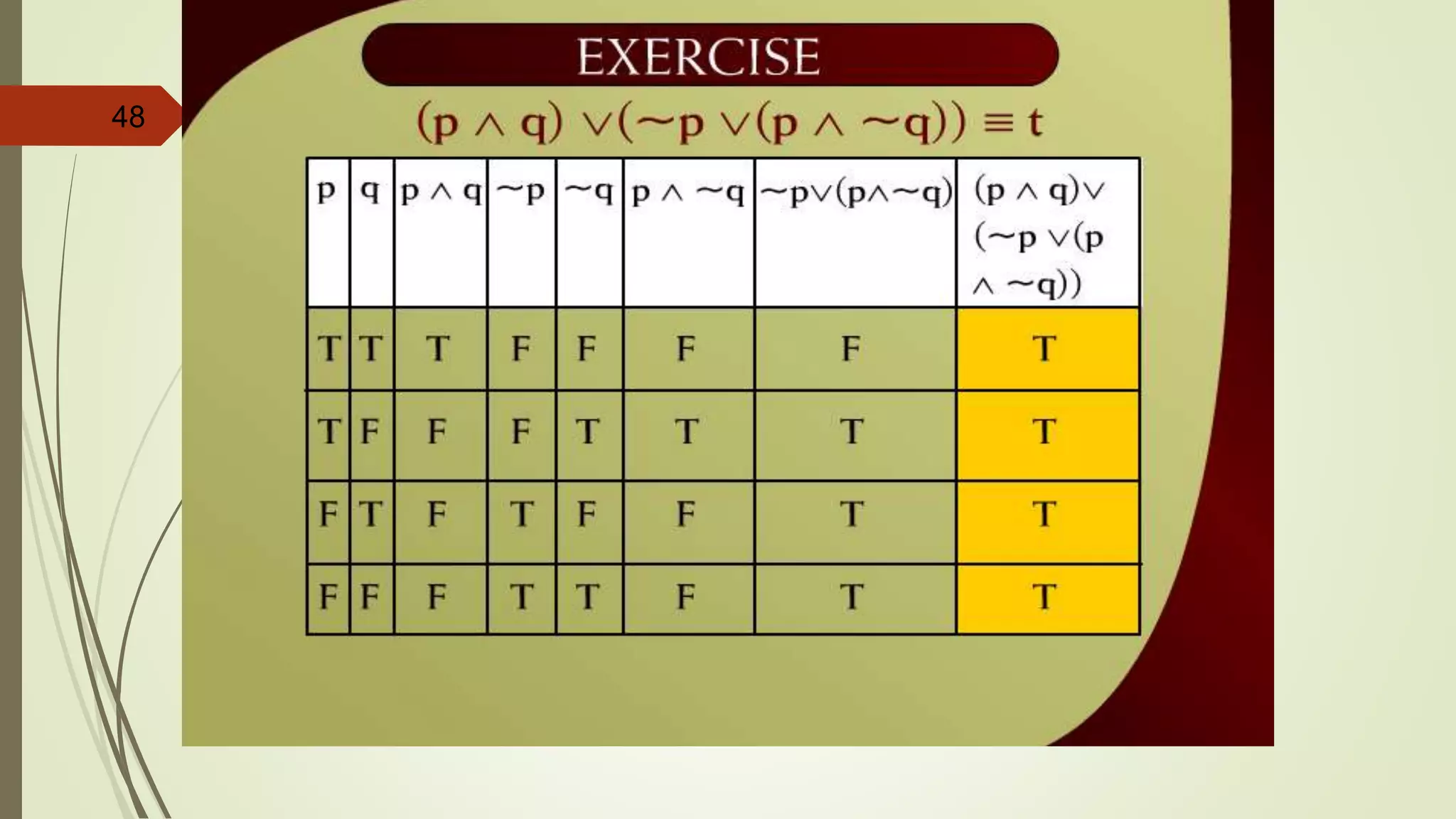
55. APPLYING LAWS OF LOGIC
 p  [~(~p  q)]

56. 56
Application - 1

57. APPLYING LAWS OF LOGIC
 ~ (~ p  q)  (p  q)

58. 58 Example - 2

59. 59 Simplifying a Statement – 3

60. 60
Distributive Law in Reverse – 4

61. 61 Exercise – 5

62. 62 Exercise - 5a

63. 63 Conditional Statements - 6

64. 64 Conditional Statements – 6a

65. 65 Truth Table for p  q - 8

66. 66
Conditional Statements or
Implications - 7

67. 67
Conditional Statements OR
Implications – 7a

68. Conditional statements
 A friend tells you “If you upload that picture to Facebook, you’ll lose your job.”
Under what conditions can you say that your friend was wrong?
 There are four possible outcomes:
1. You upload the picture and lose your job
2. You upload the picture and don’t lose your job
3. You don’t upload the picture and lose your job
4. You don’t upload the picture and don’t lose your job
There is only one possible case in which you can say your friend was wrong: the
second outcome in which you upload the picture but keep your job. In the last two
cases, your friend didn’t say anything about what would happen if you didn’t upload
the picture, so you can’t say that their statement was wrong.
Even if you didn’t upload the picture and lost your job anyway, your friend never said
that you were guaranteed to keep your job if you didn’t upload the picture; you
might lose your job for missing a shift or punching your boss instead.

69. Conditional statement : If p is true then q
is true
P Q P->Q ~p ~P v Q
T T T F T
T F F F F
F T T T T
F F T T T
So, when the hypothesis is false the statement is vacuously true.
or
When the hypothesis is not true the conclusion is irrelevant.
If I am the prime minister of Pakistan, then I am a Pakistani citizen

70. Conditional statement : If p is true then q
is true
 If I study hard, then I will pass VS Either I don’t study hard, or I pass
 If earth is flat then, 2=3
 If it is raining, then there are clouds is the sky

71. 71 Example – 9

72. 72 Example – 9

73.  For any conditional, there are three related statements, the converse, the inverse,
and the contrapositive.
1. The original conditional is "if p, then q′′ p→q
2. The converse is "if q, then p′′ q→p
3. The inverse is "if not p, then not q′′ ∼p→∼q
4. The contrapositive is "if not q, then not p′′ ∼q→∼p

74.  Consider again the conditional “If it is raining, then there are clouds in the sky.” It
seems reasonable to assume that this is true.
 The converse would be “If there are clouds in the sky, then it is raining.” This is not
always true.
 The inverse would be “If it is not raining, then there are no clouds in the sky.” Likewise,
this is not always true.
 The contrapositive would be “If there are no clouds in the sky, then it is not raining.”
This statement is true and is equivalent to the original conditional.

76. “If I eat this giant cookie, then I will feel sick.” If this statement is true which of the following
statements must also be true ?
1. If I feel sick, then I ate that giant cookie.
2. If I don’t eat this giant cookie, then I won’t feel sick.
3. If I don’t feel sick, then I didn’t eat that giant cookie.
Solution
1. This is the converse, which is not necessarily true. I could feel sick for some other reason,
such as drinking sour milk.
2. This is the inverse, which is not necessarily true. Again, I could feel sick for some other
reason; avoiding the cookie doesn’t guarantee that I won’t feel sick.
3. This is the contrapositive, which is true, but we have to think somewhat backwards to explain
it. If I ate the cookie, I would feel sick, but since I don’t feel sick, I must not have eaten the
cookie.

77. “If you microwave salmon in the staff kitchen, then I will be mad at you.” If this statement is true,
which of the following statements must also be true?
1. If you don’t microwave salmon in the staff kitchen, then I won’t be mad at you.
2. If I am not mad at you, then you didn’t microwave salmon in the staff kitchen.
3. If I am mad at you, then you microwaved salmon in the staff kitchen.
Solution : Choice b is correct because it is the contrapositive of the original statement.

78. Consider the statement “If you park here, then you will get a ticket.” What set of conditions would
prove this statement false?
1. You don’t park here, and you get a ticket.
2. You don’t park here, and you don’t get a ticket.
3. You park here and you don’t get a ticket.
The first two statements are irrelevant because we don’t know what will happen if you park somewhere
else. The third statement, however, contradicts the conditional statement “If you park here, then you
will get a ticket” because you parked here but didn’t get a ticket.
This example demonstrates a general rule; the negation of a conditional can be written as a
conjunction: “It is not the case that if you park here, then you will get a ticket” is equivalent to “You
park here and you do not get a ticket.”
The negation of a conditional statement is equivalent to a conjunction of the hypothesis and the
negation of the conclusion.
∼(p→q) is equivalent to p∧∼q

79. Which of the following statements is equivalent to the negation of “If you don’t grease the
pan, then the food will stick to it” ?
1. I didn’t grease the pan and the food didn’t stick to it.
2. I didn’t grease the pan and the food stuck to it.
3. I greased the pan, and the food didn’t stick to it.
Solution
1. This is correct; it is the conjunction of the hypothesis and the negation of the conclusion.
To disprove that not greasing the pan will cause the food to stick, I have to not grease
the pan and have the food not stick.
2. This is essentially the original statement with no negation; the “if…then” has been
replaced by “and”.
3. This essentially agrees with the original statement and cannot disprove it.

80. “If you go swimming less than an hour after eating lunch, then you will get cramps.” Which of the
following statements is equivalent to the negation of this statement?
1. I went swimming more than an hour after eating lunch and I got cramps.
2. I went swimming less than an hour after eating lunch and I didn’t get cramps.
3. I went swimming more than an hour after eating lunch and I didn’t get cramps.
Solution: choice b is equivalent to the negation; it keeps the first part the same and negates the
second part.

81. Biconditional statements
 A biconditional is a logical conditional statement in which the hypothesis and
conclusion are interchangeable.
 A biconditional is written as p↔q and is translated as " p if and only if q′′ .
P Q P <-> Q
T T T
T F F
F T F
F F T

82. Biconditional statements "p if and only if
q′′
 “The garbage truck comes down my street if and only if it is Thursday morning.” Which
of the following statements could be true?
1. It is noon on Thursday and the garbage truck did not come down my street this morning.
2. It is Monday and the garbage truck is coming down my street.
3. It is Wednesday at 11:59PM and the garbage truck did not come down my street today.
 Solution
1. This cannot be true. This is like the second row of the truth table; it is true that I just
experienced Thursday morning, but it is false that the garbage truck came.
2. This cannot be true. This is like the third row of the truth table; it is false that it is
Thursday, but it is true that the garbage truck came.
3. This could be true. This is like the fourth row of the truth table; it is false that it is
Thursday, but it is also false that the garbage truck came, so everything worked out
like it should.

83. Biconditional statements "p if and only if
q′′
 Suppose this statement is true: “I wear my running shoes if and only if I am
exercising.” Determine whether each of the following statements must be true or
false.
 I am exercising and I am not wearing my running shoes.
 I am wearing my running shoes and I am not exercising.
 I am not exercising, and I am not wearing my running shoes.

84. Biconditional statements "p if and only if
q′′
 Suppose your boss needs you to do either project A or project B (or both, if you
have the time). You will not get a bad review if and only if you do project A or
project B. Make the truth table for this scenario.

85. 1. Identify atomic propositions
2. Determine appropriate logical connections
 If I go to the store or the movies, I won't do my homework
85
Translating English Sentences to
Symbols

86. 86 Translating English Sentences to
Symbols – 12a

87. 87 Translating English Sentences to
Symbols – 12a

88. 88
Translating English Sentences to
Symbols – 12b

89. 89
Translating English Sentences to
Symbols – (3 – 12c)

90. 90
Translating Symbolic Propositions
to English – 13

91. 91
Translating Symbolic Propositions
to English – 13a

92. 92
Translating Symbolic Propositions
to English – 13a

93. 93
Translating Symbolic Propositions
to English – 13b

94. 94
Translating Symbolic Propositions
to English – 13b

95.  You can get a free sandwich on Thursday if you buy a sandwich or a cup of tea
 You can get a free sandwich on Thursday only if you buy a sandwich or a cup
of tea
 The automated reply can't be sent when the system is full

96. 96
Hierarchy of Operations for Logical
Connectives - 14

97. 97 Truth Table for p v ~ q ~ p – 20a

98. 98 Truth Table for p v ~ q ~ p – 20a

99. 99 Truth Table for p v ~ q ~ p – 20b

100. 100 (p  q) (~p  r) - 21

101. 101 (p  q) (~p  r) - 21

102. 102 (p  q) (~p  r) – 21a

103. 103
(p  q) (~p  r) – 21c

104. Solving Logic Puzzles
 An island has two kinds of inhabitants, knights, who always tell the truth and
knaves, who always lie. You go to the island and meet A and B. A says “B is a
knight”. B says, “ The two of us are of opposite types.”. What are A and B.
 When planning a party, you want to know whom to invite. Among the people you
would like to invite are three touchy friends. You know that if Sara attends, she will
become unhappy if Anum is there, Anum will attend only if Meral will be there, and
Meral will not attend unless Sara also does. Which combinations of these three
friends can you invite so as not to make someone unhappy.

105. Quiz will be held on 5th October 2022 if and only
it its Wednesday and we have a class.