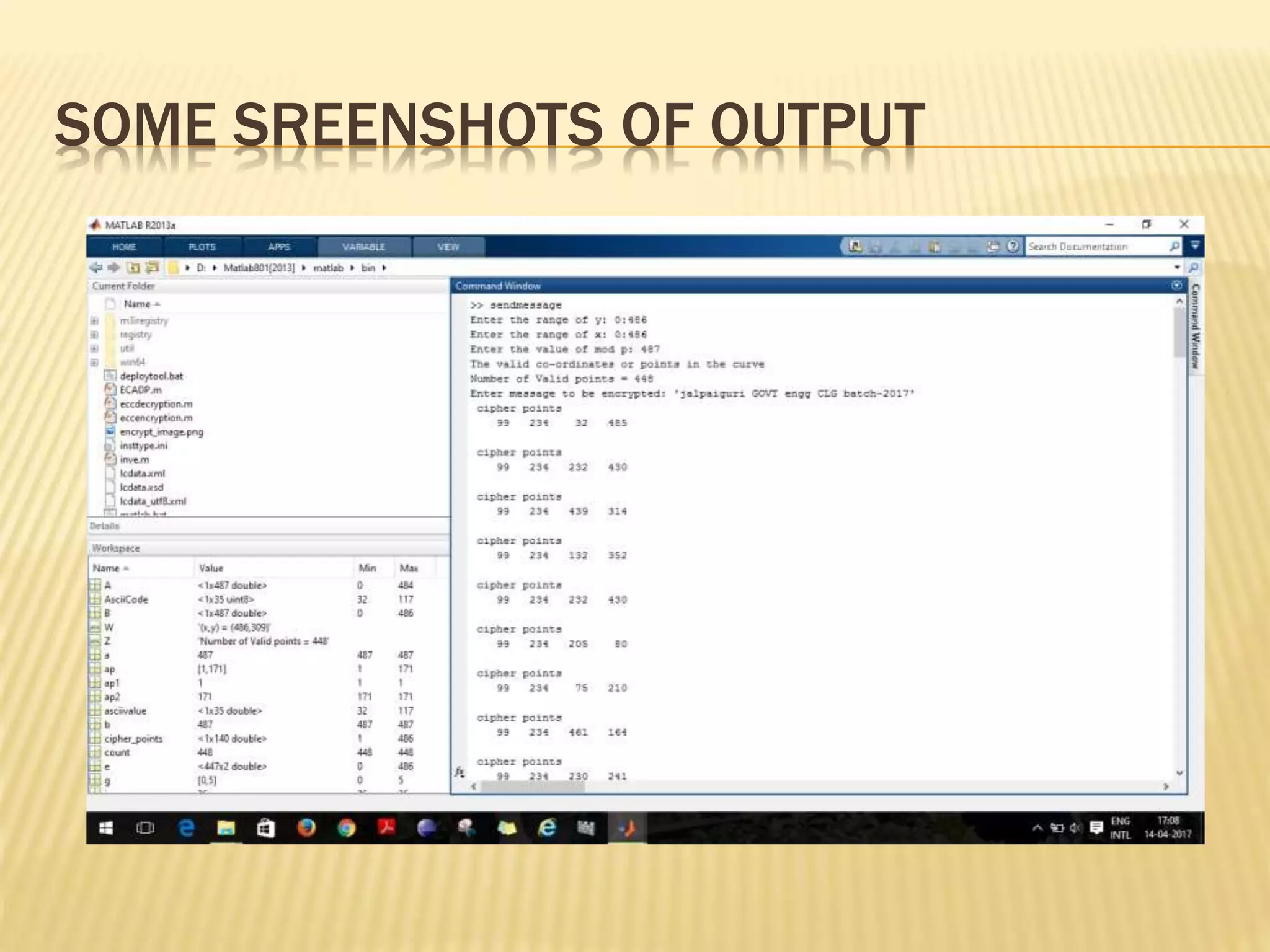
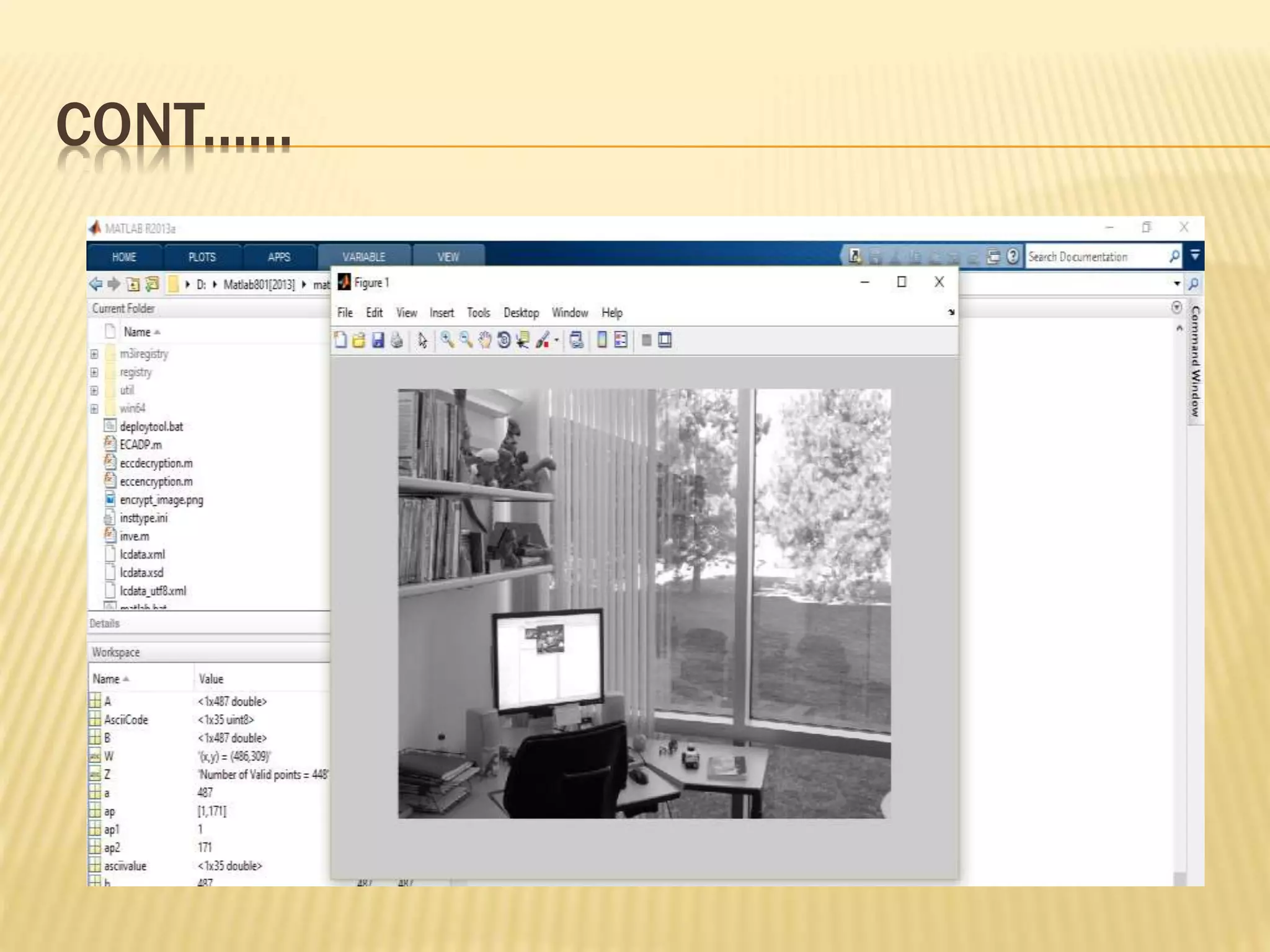
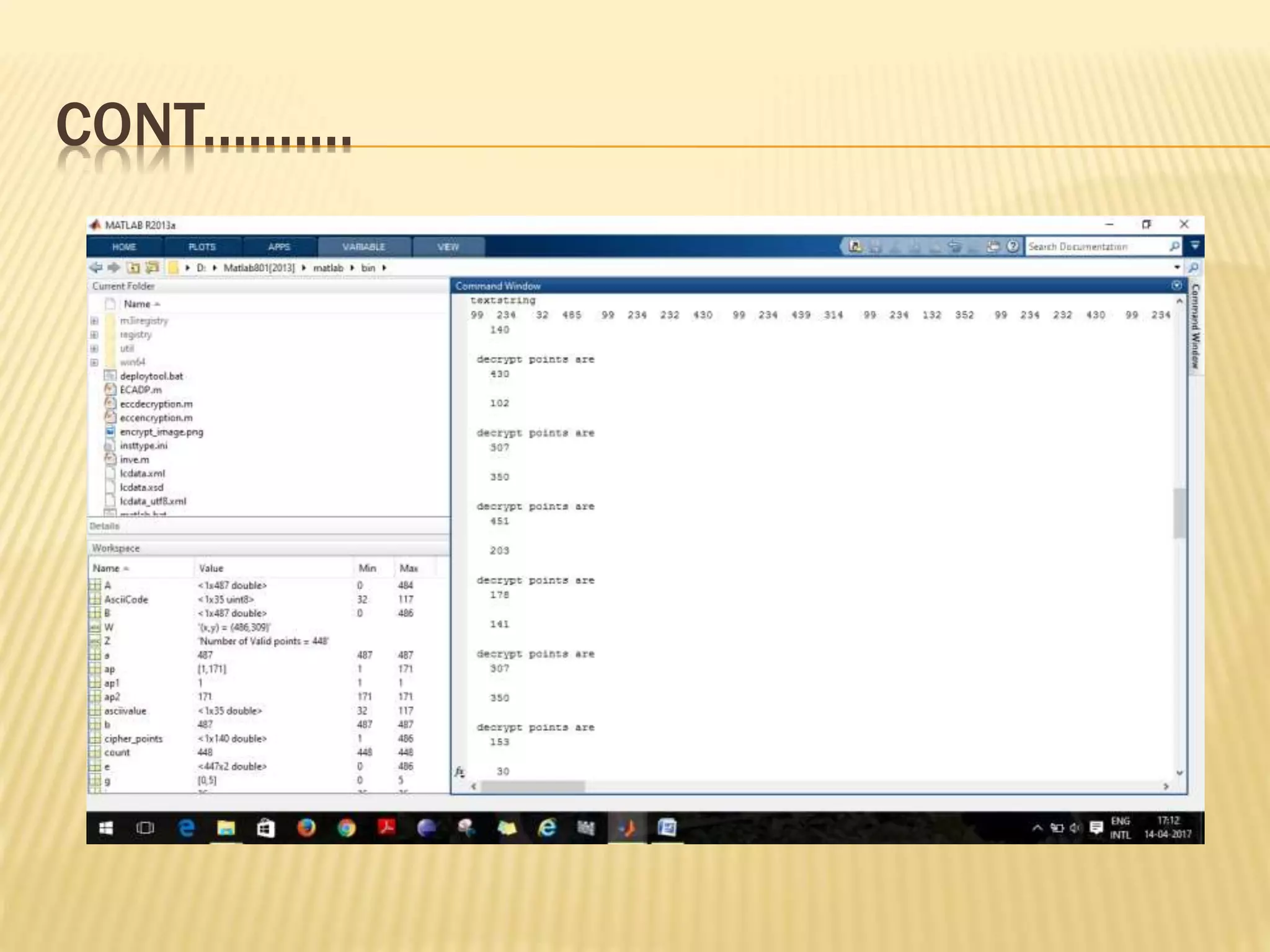
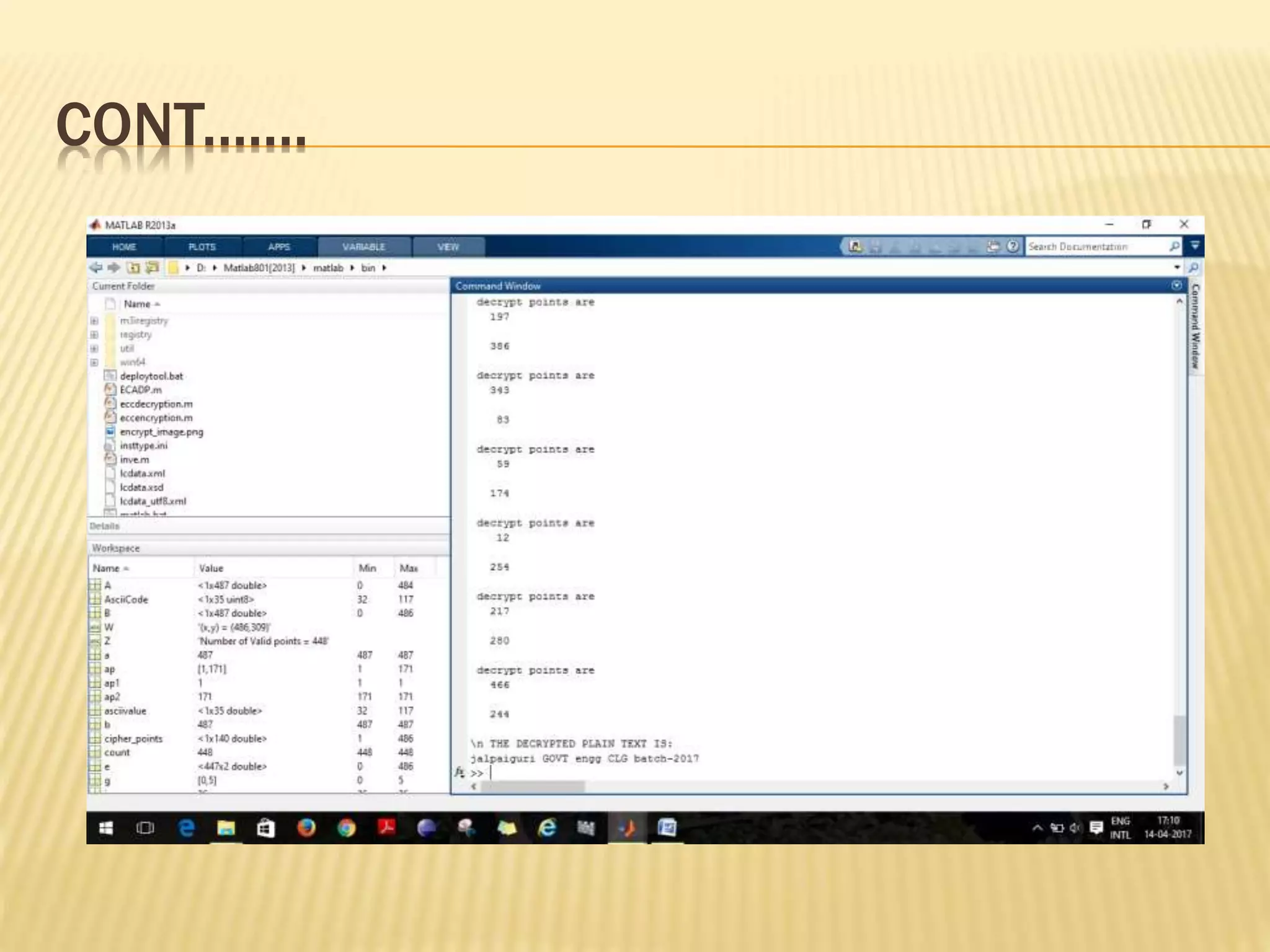
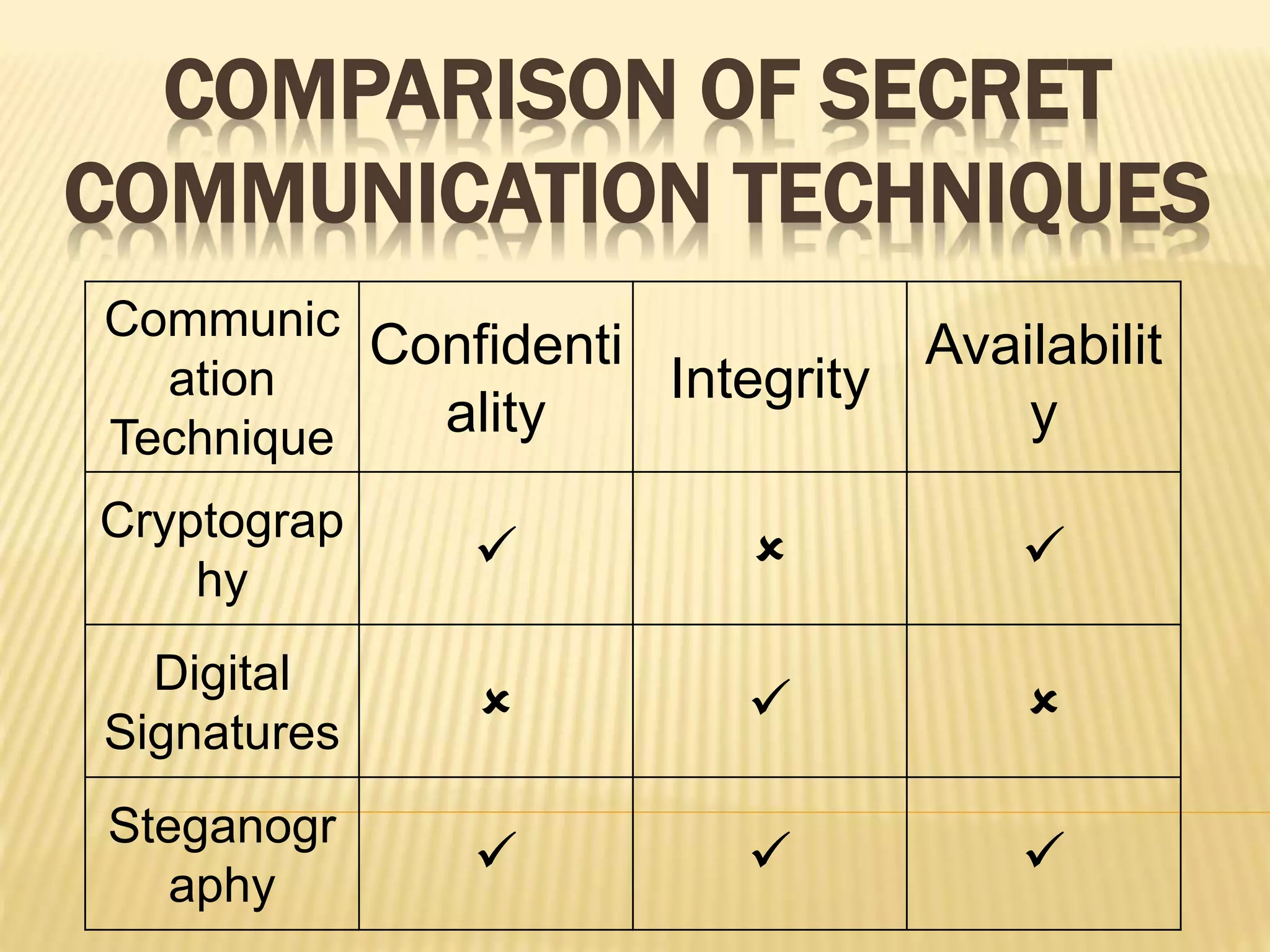
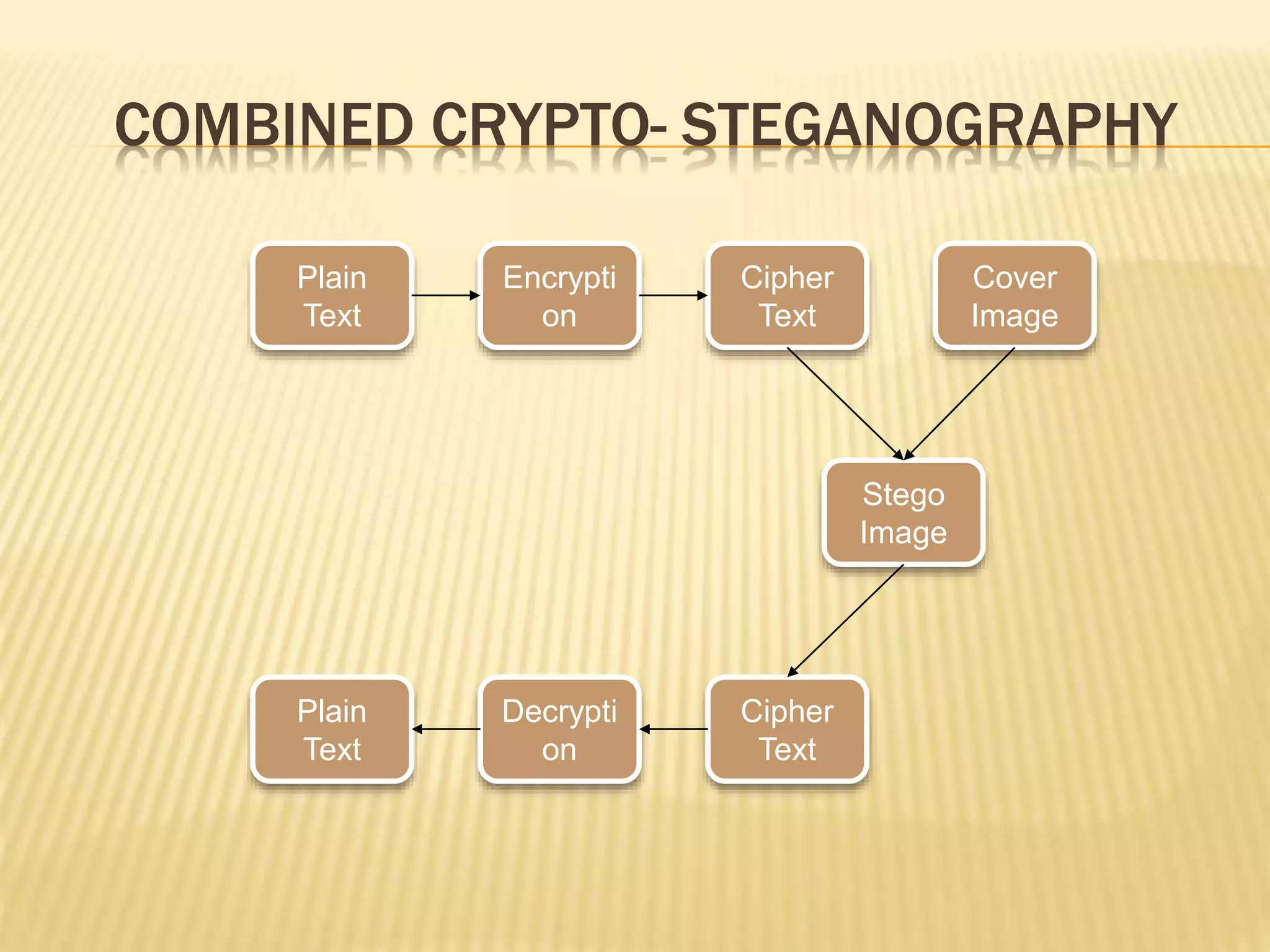
The document discusses an improved security system utilizing steganography and elliptic curve cryptography to ensure secure data transmission over networks, addressing the growing need for data protection from unauthorized access. It outlines key cryptographic concepts, techniques for image steganography, and proposes a combined approach to enhance security through dual methods of encryption and data concealment. The conclusion emphasizes the effectiveness of the model for secure communications in sensitive fields such as defense, banking, and government operations.

1. IMPROVED SECURITY SYSTEM USING
STEGANOGRAPHY AND ELLIPTIC CURVE
CRYPTOGRAPHY
GUIDED BY
PROF.CHINMOY GHOSH
Group members:-
Manisha Agarwal
Anwesha Bhowmik
Atanu Deb
Atanu Roy

2. ACKNOWLEDGEMENT
We take this opportunity to express our
profound gratitude and deep regards to our
project mentor Prof. Chinmoy Ghosh and
our Head of the Department Prof. Shrayasi
Datta of Information Technology
Department, Jalpaiguri Government
Engineering College, for example guidance,
monitoring and constant encouragement
throughout the course to present this report.

3. DISCUSSION GOALS
 INTRODUTION
 KEY TERMS
 BASIC TERMS OF CRYPTOGRAPHY
 BASE CRYPTOGRAPHY MECHANISM
 CRYPTOGRAPHY ISSUES
 CRYPTOSYSTEM SERVICES OR SECURITY GOALS
 PROPOSED ECC TECHNIQUE AND EXAMPLE
 STEGANOGRAPHY AND ITS TERMS
 IMAGE STEGANOGRAPHY
 LSB SUBSTITUTION
 COMBINED CRYPTO-STEGANOGRAPHY
 ENCRYPTION AND LSB EMBEDDING
 DECRYPTION
 BABY STEP GIANT STEP
 SCREENSHOTS
 FURURE SCOPE
 CONCLUSION

4. INTRODUCTIONProblem Statement :
Nowadays, tons of data pass through various network, some of
them are very much confidencial and crucial. Attackers are always
waiting to manipulate and corrupt the data for evil motives. Now, it is
very much important to secure the data so that it remains intact in
the time of communication.
Data integration can be hampered in case of absence of network
security . So, for trusted transmission of data over networks it is
mandatory to have a good network security policy .
Objectives:
The main objectives of the project is to make the data safe and
secure and transmit the data in such a way that it is not possible for
anyone to detect the data . Steganography is concealing the secret
message in non secret image. Whereas Encryption is converting
data into code to prevent unauthorized access .Steganography as
well as cryptography has its own disadvantage. Our objective is to
implement both the procedures to enforce tight security and to
prevent evesdropping etc.

5. KEY TERMS :-
 Cryptography : deals with hiding information in such a way that
allows information to be sent in a secure form so that only person
able to retrieve hided information is the intended recipient. In
present times, cryptography is considered as a branch of both
mathematics and computer science, and is affiliated closely with
information theory, information security and engineering
technology.
 Steganography: Steganography is one of the most powerful
techniques to conceal the existence of hidden secret data inside
a cover object. Images are the most popular cover objects for
Steganography and in this work image steganography is
adopted.Steganography is the art and science of communicating
in a way which hides the existence of the communication.
Steganography plays an important role in information security. It
is the art of invisible communication by concealing information
inside other information.

6. BASIC TERMS OF CRYPTOGRAPHY
 Cipher: the algorithm that does the encryption.
 Ciphertext: the encrypted (scrambled) version of the message. Message altered to
be unreadable by anyone except the intended recipients.
 Cryptanalysis: the science of breaking cryptographic algorithms.
 Cryptanalyst: a person who breaks cryptographic codes; also referred to as “the
attacker”.
 Cryptosystem – The combination of algorithm, key, and key management functions
used to perform cryptographic operations.
 Decryption: the process of converting ciphertext back to the original plaintext.
 Encryption: scrambling a message or data using a specialized cryptographic
algorithm.
 Key – Sequence that controls the operation and behavior of the cryptographic
algorithm.
 Plaintext – A message in its natural format readable by an attacker.

7. BASE CRYPTOGRAPHY MECHANISM
Encryption
Algorithmplaintext
Ciphertext
plaintext
Lyon
Juvia
Gray
Decryption
Algorithm
Key A Key B

8. CRYPTOGRAPHY ISSUES
CIA Traid

9. CRYPTOSYSTEM SERVICES OR SECURITY GOALS
Authentication
 Ensures that whoever supplies or accesses sensitive data is an
authorized party.
Confidentiality
 Assures that only authorized parties are able to understand the data.
Integrity
 Ensures that when a message is sent over a network, the message
that arrives is the same as the message that was originally sent.
Nonrepudiation
 Ensuring that the intended recipient actually received the message &
ensuring that the sender actually sent the message.

10. PROPOSED ECC TECHNIQUE
A general Elliptic Curve equation takes the general form:
Yˆ2= xˆ3+ ax + b ………………(1)
(x, y) = co-ordinates on the EC.
a, b = coefficients
However for finite fields a modified equation is used [5]:
yˆ2 mod p = (xˆ3+ax + b) mod p (2)
where p = prime number for which the EC be defined
a, b satisfy the equation [2]
(4a3+ 27b2 ) mod p ≠ 0 mod p ………………… (3)
An elliptic curve E over GF (p) consist of the solutions (x, y) defined
by (1) and (2), along with an additional element
called 0, which is the point of EC at infinity. The set of points (x, y)
are said to be affine coordinate point representation.
The basic operations on elliptic curves are addition and doubling. A
scalar multiplication with a point can be
represented as a combination of addition operations.

11. CONT.............
Say, given a point P (x, y) is to be multiplied k times, say k = 37. Thus we have
to calculate 37P.
In terms of addition it can be represented as
37P = P + P + P +… + P (37 times)
For addition of two points P(x1, y1) & Q(x2, y2). First calculate the tangent to
the curve at point P [5].
L = [(y2- y1)/(x2-x1)] mod p, for x1 ≠ x2 (4)
L = [(3x1ˆ2+ a)/ 2yP] mod p, for x1 = x2 (5)
P+Q = R
x3 = (L2 - x1 - x2) mod p
y3 = (L (x1 - x3) –y2] mod p
where Q = (x2, y2) = co-ordinates of Q change with every addition method
applied, i.e. after first addition its co-ordinates
will be (x3, y3), and so on.
L = tangent to the curve at point P.
R = (x3, y3), resultant co-ordinates
Thus applying addition methods, determined by the value of ‗k‘, we obtain
point R (x3, y3). Each point thus obtained
is also an affine point on the Elliptic Curve.

12. EXAMPLE – ELLIPTIC CURVE CRYPTOSYSTEM
• Suppose Alice wants to send to Bob an encrypted message.
– Both agree on a base point, B.
– Alice and Bob create public/private keys.
• Alice
– Private Key = a
– Public Key = PA = a * B
• Bob
– Private Key = b
– Public Key = PB = b * B
– Alice takes plaintext message, M, and encodes it onto a point, PM, from the
elliptic group.
Alice chooses another random integer, k from the interval [1, p-1]
– The ciphertext is a pair of points
• PC = [ (kB), (PM + kPB) ]
– To decrypt, Bob computes the product of the first point from PC and his private
key, b
• b * (kB)
– Bob then takes this product and subtracts it from the second point from PC
• (PM + kPB) – [b(kB)] = PM + k(bB) – b(kB) = PM

13. WHAT IS STEGANOGRAPHY?
 Steganography is the art and science of writing hidden messages in
such a way that no one, apart from the sender and intended recipient,
suspects the existence of the message, a form of security through
obscurity.
STEGONOG
RAPHY
EXAMPLE
RANDOM TEXT
Since everyone can read,
encoding text
in neutral sentences is
doubtfully effective
SOME HIDDEN
PATTERN
Since Everyone Can Read,
Encoding Text
In Neutral Sentences Is
Doubtfully Effective
ORIGINAL
MESSAGE
SECRET INSIDE

14. STEGANOGRAPHY TERMS
 Carrier or Cover File - A Original message or a file
in which hidden information will be stored inside of
it .
 Stego-Medium - The medium in which the
information is hidden.
 Embedded or Payload - The information which is
to be hidden or concealed.
 Steganalysis - The process of detecting hidden
information inside a file.

15. IMAGE STEGANOGRAPHY
 Using image files as hosts for steganographic messages takes
advantage of the limited capabilities of the human visual system
 Some of the more common method for embedding messages in image
files can be categorized into two main groups, image domain methods
and transform domain methods
Image And Transform Domain:
 Image – also known as spatial – domain techniques embed messages in
the intensity of the pixels directly, while for transform – also known as
frequency – domain, images are first transformed and then the message
is embedded in the image
 Image domain techniques encompass bit-wise methods that apply bit
insertion and noise manipulation and are sometimes characterized as
“simple systems”
 Steganography in the transform domain involves the manipulation of
algorithms and image transforms

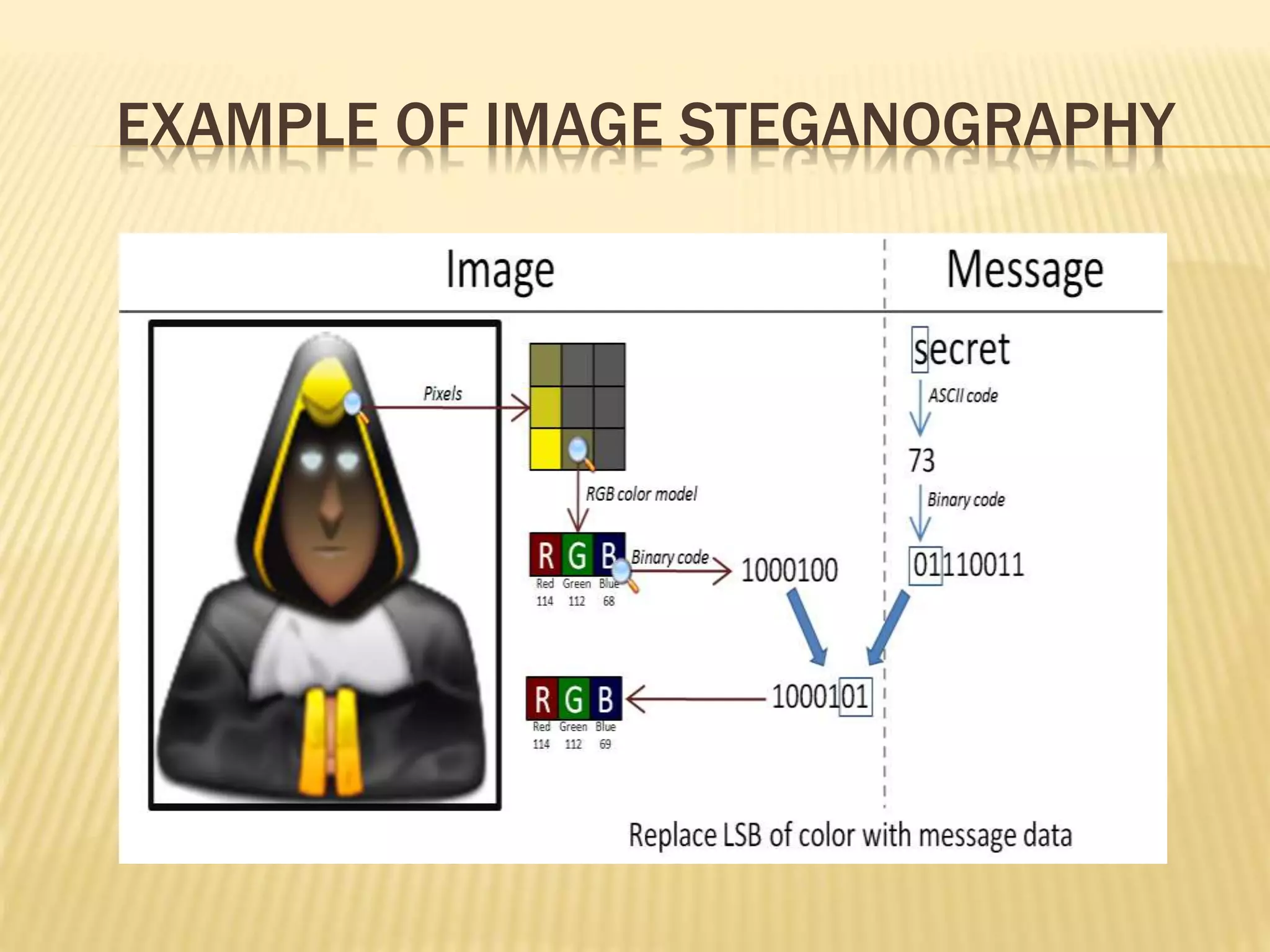
16. LSB [LEAST SIGNIFICANT
BIT] METHOD
 Least significant bit (LSB) insertion is a common, simple
approach to embedding information in a cover image
 The least significant bit (in other words, the 8th bit) of some or
all of the bytes inside an image is changed to a bit of the secret
message
 When using a 24-bit image, a bit of each of the red, green and
blue color components can be used, since they are each
represented by a byte. In other words, one can store 3 bits in
each pixel. An 800 × 600 pixel image, can thus store a total
amount of 1,440,000 bits or 180,000 bytes of embedded data
 In its simplest form, LSB makes use of BMP images, since
they use lossless compression

17. EXAMPLE OF IMAGE STEGANOGRAPHY

18. COMPARISON OF SECRET
COMMUNICATION TECHNIQUES
Communic
ation
Technique
Confidenti
ality
Integrity
Availabilit
y
Cryptograp
hy
  
Digital
Signatures
  
Steganogr
aphy
  

19. COMBINED CRYPTO- STEGANOGRAPHY
Plain
Text
Stego
Image
Cipher
Text
Decrypti
on
Cipher
Text
Plain
Text
Encrypti
on
Cover
Image

20. ENCRYPTION AND LSB EMBEDDING
 INPUT: Elliptic Curve Domain parameters (p, E, P, n),
public key Q, Plaintext m, message image I, Cover
image C. OUTPUT: Stego-image CI, Stego key
 1. Represent the message ‘m’ as a point M in E (𝐹𝑝).
 2. Select K ∈𝑅[1, n-1].
 3. Compute 𝐶1=k×𝑒1(𝑥1,𝑦1)
 4. Compute 𝐶2= M +k×𝑒2(𝑥2,𝑦2).
 5. RGB cover image=C.
 6. Hide (C1, C2) into I using LSB Steganography.
 7. Hide I into C using Steganography.
 8. Return (CI)

21. DECRYPTION
 INPUT: Elliptic Curve Domain parameters (p,
E, P, n), Private key d, stego-image CI, stego
key. OUTPUT: (message m, image I)
 1. Extract I from CI Extract 𝐶1,𝐶2 from I
 2. Compute M = 𝐶2 -d×𝐶1 and compute m
from M
 3. Return (m, I)

22. BABY STEP, GIANT STEP METHOD
This is one of the fastest general methods of solving the EC discrete log problem. (In fact,it
can be applied to an arbitrary group.) The algorithm runs in approximately N time and N
space, where N = #E (Fq). This is not fast enough to be practical.
 Problem:
 Find k such that kP = Q on E(Fq), with #E(Fq) = N, assuming that such a k exists.
 Breaking Elliptic Curve Cryptosystem 38
 ALGORITHM
 1. Pick an integer m > N .
 2. Compute mP.
 3. For i = 0 to i = m-1 compute (and store) Q-iP.
 4. For j = 1 to j = m-2 compute (and store) jmP .
 5. Sort the lists from steps 3, 4 in some consistent way.
 6. Compare the lists from steps 3, 4 until a pair i, j such that Q-iP = jmP is found.
 7. Return k = i + jm (mod N).
 Here,
 N= #E(Fq), order of the elliptic curve.
 P is the generator point of the set of points of the elliptic curve.
 k is any integer.
 Q is any point on the curve.

23. SOME SREENSHOTS OF OUTPUT

24. CONT......

25. CONT..........

26. CONT.......

27. FUTURE SCOPE
 One can try using random and pseudo random
number generators for choosing the secret
integer k, and the private key .
 ECC is a vase field where there is large scope
for higher research.
 There are many more steganographic
techniques which provide data security.
 The LSB algorithm used can be extended to
more bits of lsb substitution.
 Lastly,further research may result generate
other scope on the project.

28. CONCLUSION
The proposed model introduced above is a combination
of cryptography and Steganography. The goal of the
technique is to put the unauthorized person in a
difficult position to determine the presence of
information. The dual security makes the information
more secure. With this model any one can easily send
multiple information to the receiver using public
network. This model is very useful for defense,
corporate, banking, communication and different
government portals where information exchange is
more crucial. The data hiding capacity in audio and
video is more than image, so in future using audio or
video steganography and cryptography huge amount
of data will transmit in public network without security
violence.