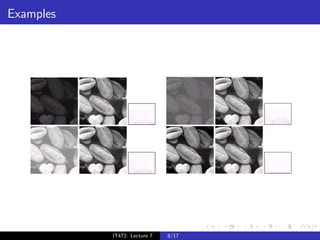
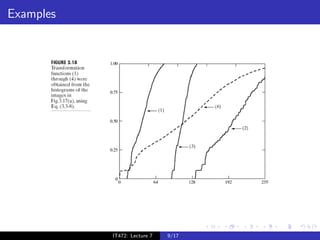
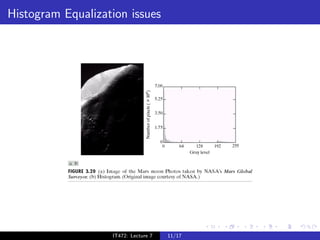
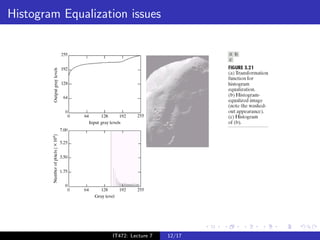
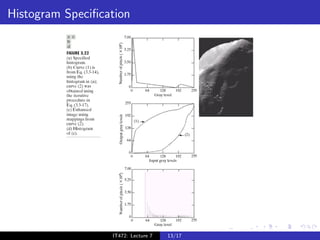
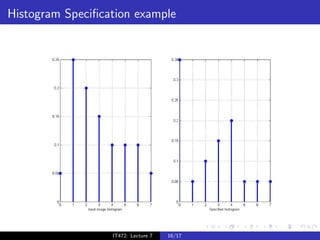
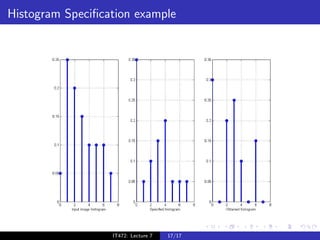
The document discusses histograms and histogram equalization for digital image processing. It defines a histogram as estimating the probability distribution function of gray values in an image and providing insight into an image's contrast. Histogram equalization is introduced as a technique that transforms an image's gray values such that the transformed values are uniformly distributed, improving contrast by spreading out the most frequent intensities. The key steps of histogram equalization are outlined.

![Histogram
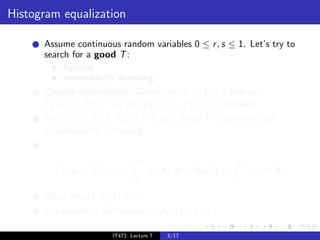
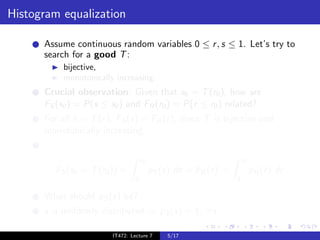
The i th histogram entry for a digital image is
M N
1
h(ri ) = χri (f [i, j]), 0 ≤ ri ≤ L − 1,
MN
i=1 j=1
where
χri (f [i, j]) = 1 if f [i, j] = ri
= 0 otherwise
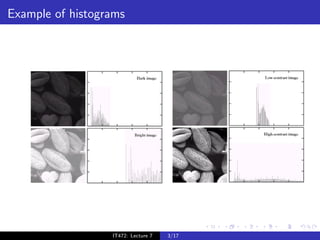
Estimates the probability distribution function of gray values
in an image.
Gives a good idea of contrast in an image.
IT472: Lecture 7 2/17](https://image.slidesharecdn.com/lecture5-120203150821-phpapp02/85/Image-Processing-4-2-320.jpg)
![Histogram
The i th histogram entry for a digital image is
M N
1
h(ri ) = χri (f [i, j]), 0 ≤ ri ≤ L − 1,
MN
i=1 j=1
where
χri (f [i, j]) = 1 if f [i, j] = ri
= 0 otherwise
Estimates the probability distribution function of gray values
in an image.
Gives a good idea of contrast in an image.
IT472: Lecture 7 2/17](https://image.slidesharecdn.com/lecture5-120203150821-phpapp02/85/Image-Processing-4-3-320.jpg)
![Histogram
The i th histogram entry for a digital image is
M N
1
h(ri ) = χri (f [i, j]), 0 ≤ ri ≤ L − 1,
MN
i=1 j=1
where
χri (f [i, j]) = 1 if f [i, j] = ri
= 0 otherwise
Estimates the probability distribution function of gray values
in an image.
Gives a good idea of contrast in an image.
IT472: Lecture 7 2/17](https://image.slidesharecdn.com/lecture5-120203150821-phpapp02/85/Image-Processing-4-4-320.jpg)