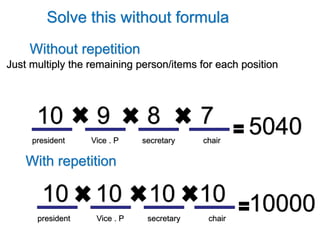
The document discusses the concepts of permutations and combinations, emphasizing the importance of order in permutations and its irrelevance in combinations. It provides examples such as selecting officers in a fraternity (permutations) and forming a committee (combinations) to illustrate the formulas and methods for calculating each. Understanding when to use permutations versus combinations requires practice and familiarity with the definitions.

1. Welcome to my presentation

3. Permutations and Combinations
An arrangement or listing in which order or placement is important is called a
permutation.
Simple example: “combination lock”
31 – 5 – 17 is NOT the same as 17 – 31 – 5

4. Permutations
An arrangement or listing in which order or placement is important is called a
permutation.
Simple example: “combination lock”
31 – 5 – 17 is NOT the same as 17 – 31 – 5
Though the same numbers are used, the order in which
they are turned to, would mean the difference in the lock
opening or not.
Thus, the order is very important.

5. The Gamma Zeta Beta fraternity is electing a President, Vice President,
Secretary, and Kegger Chair. If the fraternity has 10 members, in how
many different ways can the officers be chosen?
Position
President
Vice president
Secretary
Kegger chair
Permutations
person
A
B
C
D
Person
B
C
A
D
Select 4 person as well as their position. So, this is permutation

6. Permutation
The number of permutations of n objects taken r at a time is the quotient of
n! and (n – r)!
 !
!
rn
n
Prn


Permutations
Use the formula 10 person for 4 position
10!
10 − 4 !
10!
6!
10 ∗ 9 ∗ 8 ∗ 7 ∗ 6!
6!
5040
Formula for permutation without repetition

7. Formula for permutation with repetition
Permutations
Which is easier to write down using an exponent of r:
n × n × ... (r times) = 𝒏 𝒓
Use the formula 10 person for 4 position with allow repetition
𝟏𝟎 𝟒 10*10*10*10 10000 ways

8. Solve this without formula
Without repetition
With repetition
Just multiply the remaining person/items for each position
Vice . Ppresident secretary chair
10 789
Vice . Ppresident secretary chair
10 101010
5040
10000

9. Combinations
An arrangement or listing in which order is not important is called a combination.
"My fruit salad is a combination of apples, grapes and bananas" We don't
care what order the fruits are in, they could also be "bananas, grapes and
apples" or "grapes, apples and bananas", its the same fruit salad. It’s
combination

10. Combination
The number of combinations of n objects taken r at a time is the quotient
of n! and (n – r)! * r!
  !!
!
rrn
n
Crn


An arrangement or listing in which order is not important is called a combination.
Combinations
"My fruit salad is a combination of apples, grapes and bananas" We don't
care what order the fruits are in, they could also be "bananas, grapes and
apples" or "grapes, apples and bananas", its the same fruit salad. It’s
combination

11. Combinations
The Gamma Zeta Beta fraternity must choose a committee of four members to
plan its annual Children’s Hospital fund raiser and beer bash. If the fraternity
has 10 members, how many different committees can be chosen?
The order in which the students are chosen does not matter, so this situation
represents a combination of 10 people taken 4 at a time.

12. 401 CCrn 
Combinations
The Gamma Zeta Beta fraternity must choose a committee of four members to
plan its annual Children’s Hospital fund raiser and beer bash. If the fraternity
has 10 members, how many different committees can be chosen?
The order in which the students are chosen does not matter, so this situation
represents a combination of 10 people taken 4 at a time.
1*2*3*4!6
!6*7*8*9*10
!4)!410(
!10
410 

C
210or
24
5040

There are 35 different groups of students that could be selected.

13. Combination without repetition
𝒏!
𝒓! 𝒏 − 𝒓 !
Combination with repetition
𝒓 + 𝒏 − 𝟏 !
𝒓! 𝒏 − 𝒓 !
Where n is the number of things to choose from, and we choose r of them

14. Number of remaining person/item divided by position then multiply each slot
10
∗
9
∗
8
∗
7
Combination without repetition

15. 10
1
∗
9
2
∗
8
3
∗
7
4
Combination without repetition
Number of remaining person/item divided by position then multiply each slot

16. 10
1
∗
9
2
∗
8
3
∗
7
4
5040
24
210
Combination without repetition
Number of remaining person/item divided by position then multiply each slot

17. When working with permutations and combinations, it is vital that you
are able to distinguish when the counting order is important, or not.
This is only recognizable after a considerable amount of practice.
Combinations

18. When working with permutations and combinations, it is vital that you
are able to distinguish when the counting order is important, or not.
This is only recognizable after a considerable amount of practice.
 When the order doesn't matter, it is a Combination.
 dot When the order does matter it is a Permutation.
Combinations

19. When working with permutations and combinations, it is vital that you
are able to distinguish when the counting order is important, or not.
This is only recognizable after a considerable amount of practice.
 When the order doesn't matter, it is a Combination.
 dot When the order does matter it is a Permutation.
"My fruit salad is a combination of apples, grapes and bananas" We don't
care what order the fruits are in, they could also be "bananas, grapes and
apples" or "grapes, apples and bananas", its the same fruit salad. It’s
combination
Combinations

20. When working with permutations and combinations, it is vital that you
are able to distinguish when the counting order is important, or not.
This is only recognizable after a considerable amount of practice.
 When the order doesn't matter, it is a Combination.
 dot When the order does matter it is a Permutation.
Combinations
"The combination to the safe is 472". Now we do care about the order. "724"
won't work, nor will "247". It has to be exactly 4-7-2. it’s permutation
"My fruit salad is a combination of apples, grapes and bananas" We don't
care what order the fruits are in, they could also be "bananas, grapes and
apples" or "grapes, apples and bananas", its the same fruit salad. It’s
combination

21. A Permutation is an ordered Combination.
thought To help you to remember, think
"Permutation ... Position"