Waqas Nawaz Khokhar presented research on optimizing shortest path traversal and analysis for large graph clustering. The presentation outlined challenges with traditional graph clustering approaches for big real-world graphs. It proposed four optimizations: 1) a collaborative similarity measure to reduce complexity from O(n3) to O(n2logn); 2) identifying overlapping shortest path regions to avoid redundant traversals; 3) confining traversals within clusters to limit unnecessary graph regions; and 4) allowing parallel shortest path queries to reduce latency. Experimental results on real and synthetic graphs showed the approaches improved efficiency by 40% in time and an order of magnitude in space while maintaining clustering quality. Future work aims to address intermediate data explosion


![4
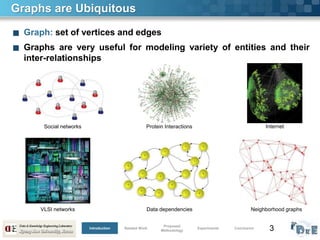
Graph Clustering
■ Graph Clustering
Partition the vertices of a graph into disjoint sets such that each partition is a
well-connected/coherent group
■ Shortest Path
A sequence of least number of edges from source to destination
■ Applications
Discovery of protein complexes [Snel ’02, Kire ‘14]
Community discovery in social networks [Newman ‘06]
Image segmentation [Shi ‘00]
Politics [Valdis ‘08]
Web Advertisement [Derry ’08, Yao ‘09]
Computational Linguistics [Matsuo ’06, Ichioka ‘08]
Many more…
Many links within a
cluster, and fewer links
between clusters
Introduction Related Work
Proposed
Methodology
Experiments Conclusion](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-4-320.jpg)
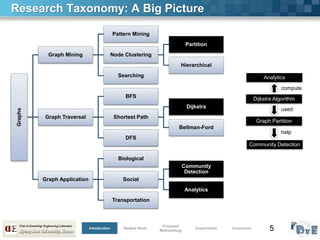
![6
Traditional Graph Clustering
■ Input: Attributed Graph
■ Process: Group Similar Vertices Together
■ Output: Clustered Graph
■ Graph Clustering is NP-Complete/Hard problem [Ref]
[Ref] Survey on Graph Clustering, by Satu Elisa Schaeffer, Computer Science Review, 2007.
Introduction Related Work
Proposed
Methodology
Experiments Conclusion](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-6-320.jpg)
![7
Challenges
■ Big Real World Graphs
Graph encodes rich relationships [Ref1]
■ Non-trivial Memory Requirements
1 Million vertices 3725 GB
1 Billion vertices 3.7 × 109 GB
• Suppose, a node pair similarity value
storage cost is 4 bytes
■ Graphs with Multiple Attributes
■ Bottleneck!!!
N2 computations for similarity
[Ref1] Managing and Mining Billion-Node Graphs by Haixun Wang (Microsoft Research Asia) in KDD 2012 Summer School
[Ref2] manyeyes.alphaworks.ibm.com
Coauthor Network of Top 200 Authors on TEL from DBLP [Ref2]
Introduction Related Work
Proposed
Methodology
Experiments Conclusion](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-7-320.jpg)

![9
Related Work
■ Scalability
Parallel and Distributed Frameworks [1,2]
• Overhead of inter-process/machine communication
Disk based approach for single PC [3,4]
• Disk data management overhead: Extensive disk I/O
• Node searching is hard, so not suitable for clustering
Relational Approach [5]
• Limited to fundamental graph operations
■ Complexity
Restricted Neighborhood Information [6-9]
Reduced Graph [10-13]
Using Evolutionary Techniques [14,15]
Sampling based Heuristics [16,17]
Limitation: Approximate / Non Exact Solutions
Introduction Related Work
Proposed
Methodology
Experiments Conclusion](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-9-320.jpg)
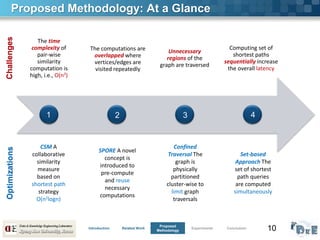
![12
Optimization 2: Shortest Path Overlapped Region (SPORE)
■ Objective
Prove the existence of shortest path overlaps
Avoid redundant/overlapped traversals
■ Idea
Identify and analyze the intersections among set of shortest paths
Maintain shortest paths (as shortcut) from current traversal for reuse
• Intuition: Sub-paths of shortest paths are also shortest paths [Ref]
• Assumption: Recently visited vertices are expected to be visited again
[Ref] Introduction to Algorithms, 2nd ed., (Cormen, Leiserson, Rivest, and Stein) 2001, p. 327.
Original Graph G SPOREs Extracted from S
P-Tree Rooted at A
Augmented Graph G’
Introduction Related Work
Proposed
Methodology
Experiments Conclusion
A C D E
B C D F
overlap
SPAE
SPBF](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-12-320.jpg)


![16
Optimization 1 Experimental Results: CSM
■ The proposed CSM [18] achieves competitive results efficiently
Introduction Related Work
Proposed
Methodology
Experiments Conclusion
ExecutionTimeQuality](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-16-320.jpg)
![17
■ SPORE [19] is able to produce an order of
magnitude less number of shortcuts as pre-
computed information efficiently
■ Pre-computed information is effective
Optimization 2 Experimental Results: SPORE
Collaboration Facebook Email
Generic graph processing model
Introduction Related Work
Proposed
Methodology
Experiments Conclusion
EfficiencyEffectiveness](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-17-320.jpg)
![18
Optimization 3 & 4 Experimental Results: Confined Traversal
■ Confined Traversal [19] improves the
execution time significantly (7~10
times)
■ We observe marginal differences in
SP distance values for both strategies
■ Execution of multiple SP queries
simultaneously reduces the overall
latency by at least 50%
Time and Expansion Analysis
Effectiveness of the Restricted Traversal (sub)
over Original Graph (full)
Analyzing the Impact of Parallelism
Introduction Related Work
Proposed
Methodology
Experiments Conclusion](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-18-320.jpg)

![20
References
[1] Bryan Perozzi et al., “Scalable-Graph-Clustering-with-Pregel”, Complex Networks, 2013.
[2] CL Staudt et al., ”Engineering High-Performance Community Detection Heuristics for Massive Graphs”, ICCP, 2013.
[3] P Sarkar et al., “Fast Nearest-neighbor Search in Disk-resident Graphs”, KDD, 2010.
[4] A Kyrola et al., “GraphChi: Large-Scale Graph Computation on Just a PC”. OSDI. Vol. 12. 2012.
[5] J Gao et al., “Relational Approach for Shortest Path Discovery over Large Graphs”, VLDB, 2012.
[6] X Fu et al., “Threshold Random Walkers for Community Detection”, Journal of Software, 2013.
[7] X Qi et al., “Optimal local community detection in social networks based on density drop of subgraphs”, Pattern
Recognition Letters, 2014.
[8] D Delling et al., “Robust Exact Distance Queries on Massive Networks”, Report by Microsoft, 2014.
[9] DA Spielman et al., “A Local Clustering Algorithm for Massive Graphs and Its Application to Nearly Linear Time Graph
Partitioning”, SIAM J. on Computing, 2013.
[10] H Shiokawa et al., “Fast Algorithm for Modularity-Based Graph Clustering”, AAAI, 2013.
[11] J Feng et al., “Compression-based Graph Mining Exploiting Structure Primitives”, ICDM, 2013.
[12] JF Rodrigues et al., “Large Graph Analysis in the GMine System”, TKDE, 2013.
[13] Y Ruan et al., “Efficient community detection in large networks using content and links”, WWW, 2013.
[14] Y Yoon et al., “Vertex Ordering, Clustering, and Their Application to Graph Partitioning”, Applied Mathematics and
information sciences, 2014.
[15] SR Mandala et al., Clustering social networks using ant colony optimization, Operational Research, 2011.
[16] B Yang et al., “Hierarchical community detection with applications to real-world network analysis”, DKE, 2013.
[17] I Rytsareva et al., “Scalable heuristics for clustering biological graphs”, IEEE Computational Advances in Bio and Medical
Sciences (ICCABS), 2013.
[18] Waqas Nawaz, Kifayat-Ullah Khan, Young-Koo Lee, and Sungyoung Lee, "Intra Graph Clustering using Collaborative
Similarity Measure", Journal of Distributed and Parallel Databases (SCIE, IF 1.0), 2015.
[19] Waqas Nawaz, Kifayat-Ullah Khan, and Young-Koo Lee, " SPORE: Shortest Path Overlapped Regions and Confined
Traversals Towards Graph Clustering", Applied Intelligence-APIN (SCI, IF 1.85), 2015.](https://image.slidesharecdn.com/icde2015symposiumwaqas-150412065827-conversion-gate01/85/ICDE-2015-Shortest-Path-Traversal-Optimization-and-Analysis-for-Large-Graph-Clustering-20-320.jpg)